机械设备振动监测的自适应变采样算法研究

段礼祥，陈瑞典，张来斌，秦天飞，王 宁

(中国石油大学(北京)机械与储运工程学院，北京 102249)

0 引言

在机械设备振动信号采集中，通常根据奈奎斯特定律以可能出现的最高故障频率来设定固定采样率。然而过高的采样率会增加数据冗余，增大采集系统能耗。该局限性尤其体现在对能耗控制要求十分严格的无线传感网络中。为了实现采集系统的低能耗，学术界与工业界进行了大量的研究工作，主要涉及到数据压缩(data compression)[1]、预测监控(predictive monitoring)[2-3]、聚合(aggregation)[4]、拓扑控制(topology management)[5-6]和自适应采样(adaptive sampling)[7-8]等技术。

在传感器节点中，数据传输的能耗要远远大于数据处理的能耗，因此可以通过减小数据传输量的方法来降低有限带宽传感器网络下的能耗[9]。另外，基于压缩感知采样技术的研究使得数据采集能够在低于奈奎斯特采样率的条件下进行，被称为亚奈奎斯特采样，主要包括随机解调器(RD)[10]，多陪集抽样(MC)[11]和调制宽带转换器(MWC)[12]3种系统框架。然而，这些方法并不属于自适应领域，无法更改参数，而且对采集终端系统外围硬件电路的设计要求十分严格，实现较为困难。

在自适应数据采集领域，HUANG Ru和ZHENG Yang等人设计了基于时间序列预测模型的自适应采样，利用先验信息不断调整采样率[13-14]，比较适用于信号变化缓慢的场合。Z.L.WANG针对基于拉曼散射的分布式温度测量系统设计了一种随光纤温度分布变化而自适应变采样的方法,但该方法只适用于此测量系统[15]。CesareAlippi等人根据奈奎斯特基本采样定律，通过信号频谱频率成分的变化来实时地调整采样率[16]，较适用于环境监测等信号变化缓慢的场合，但数据重构较为困难。

针对以上问题，本文设计了一种新的自适应数据采集算法。与目前所研究的自适应采集算法不同的是，本文不再只是考虑信号频率成分的变化来指导采集系统进行变采样，而是以机械设备健康状态监测为背景，以设备故障状态下振动信号的时域、频域特征为标准，针对性地设计变采样算法，较适用于机械状态监测等高采样率的场合。

1 机械设备振动信号的频谱特点

在振动信号的数据采集中，主要以机械设备可能出现的最高故障频率来设定固定的采样率。然而设备发生故障的时间在其整个生命周期中只占很小的比例，采用过大的固定采样率将急剧增加采集系统的能耗和存储资源压力。

本文以离心泵设备为研究对象，现取其正常与故障的2组振动信号进行频谱分析，频谱图对比结果如图1和图2所示，由图1可以看出在离心泵正常运行状态下，能够有效表征设备运行状态的信息主要集中在低于1 kHz以内的频带范围，而当设备发生故障时，如图2所示，振动信号的高频成分会发生改变，有效信息的频带范围开始扩延达到4 kHz。根据奈奎斯特定律，在离心泵正常运行状态下，只需设定大于2 kHz的采样率对信号进行采集即可，10 kHz的高采样率将极大增加采集终端CPU的持续占有率和存储资源，而当设备发生故障时则需要采用10 kHz的高采样率来获取数据，便于后续精确的数据分析。

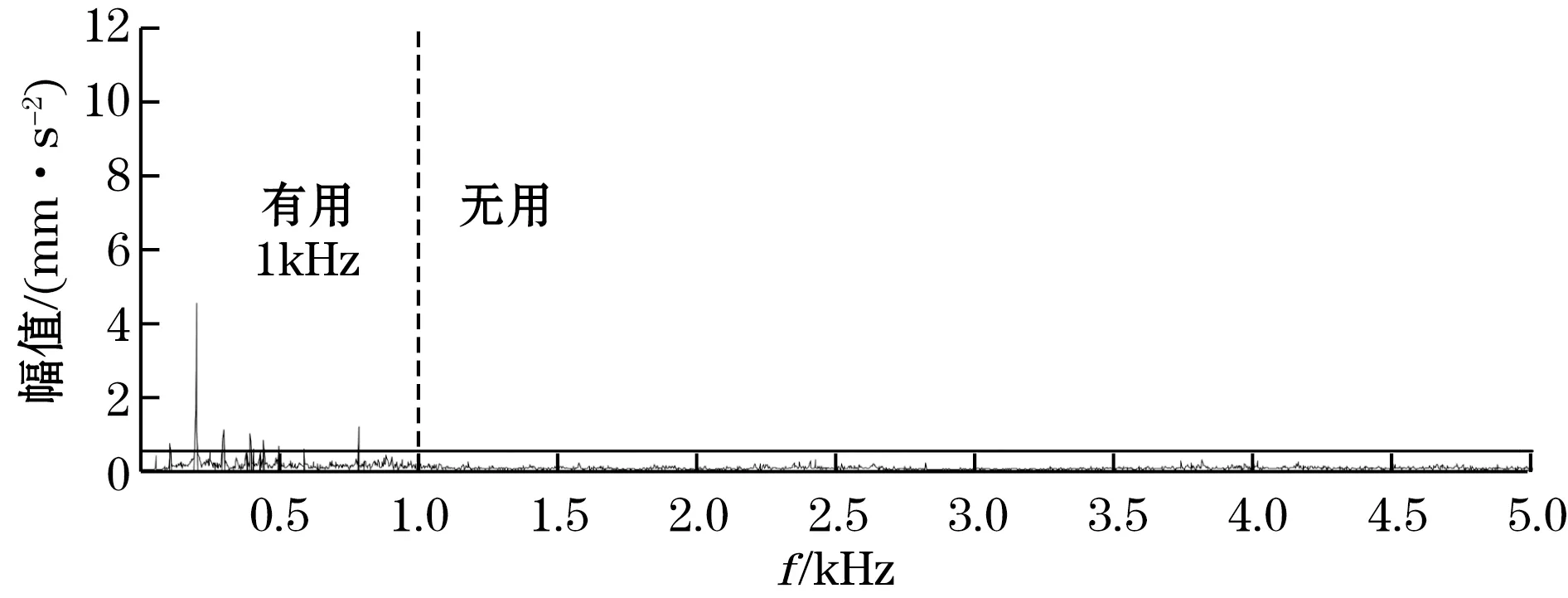
图1 离心泵正常状态下频谱图

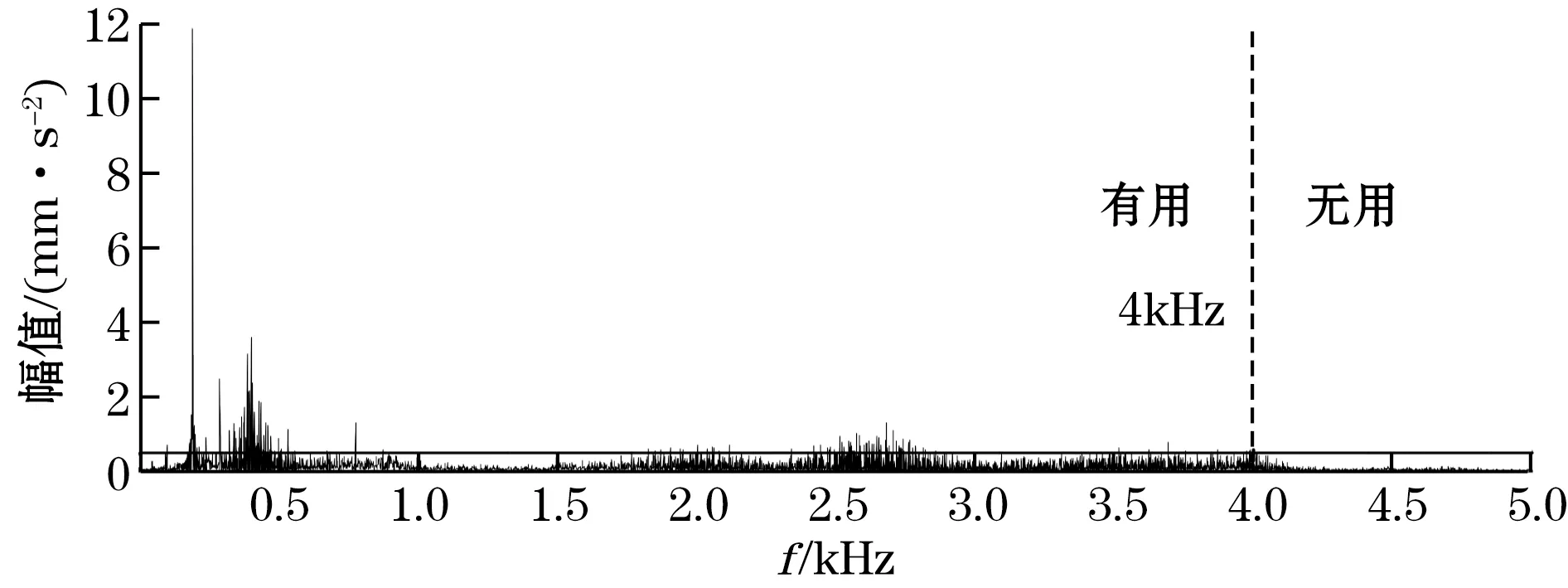
图2 离心泵故障状态下频谱图

由上可知，在机械设备状态监测数据采集中，采集系统需要具备根据设备运行状况而自适应地调整采样率的功能，即自适应变采样。

2 自适应变采样算法设计

为了保留原始信号的有效信息，并且保证采样信号的重建不失真，根据奈奎斯特定律，任何时刻的采样频率都必须大于原始信号最高分析频率的2倍。然而在实际机械设备运转过程中，受干扰、变工况和设备故障等因素的影响都会导致最高分析频率不是一个常量。而且当设备运行状态发生改变时，设备振动信号的频率和幅值成分也会随之改变。因此，机械设备状态监测下自适应数据采集算法的设计，可从信号频率成分和振动烈度两方面的变化来进行定量分析，以此指导系统自适应变采样。

为了能及时获得当前信号的信息，本文以脉冲采样来获取分析数据。脉冲采样是间断的，非周期性的，其值是根据设备最高分析频率来设定的。如图3所示，采样率分为2档，当设备在正常运行状态下，通过分析脉冲采样获得的数据得出当前只需设定较低的采样率，而当设备发生故障时，脉冲采样数据分析的结果将超出设定标准，从而指导采集系统增大采样率。另外，脉冲采样之间的时间间隔是一个可根据当前信号的波动程度而自适应调整的变量。

图3 自适应变采样过程

本文所设计的自适应变采样算法执行流程如图4所示，首先根据需要监测的机械设备设置算法的初始参数，如该设备的故障特征频率、初始脉冲采样间隔值、振动阈值等。然后对脉冲采样获取的信号进行时、频域分析，并通过信号检测模型和国家标准对分析结果进行判定，以确定下一次的采样率与脉冲采样间隔。下一次的变采样完成后，再次进入脉冲采样，以此形成循环。

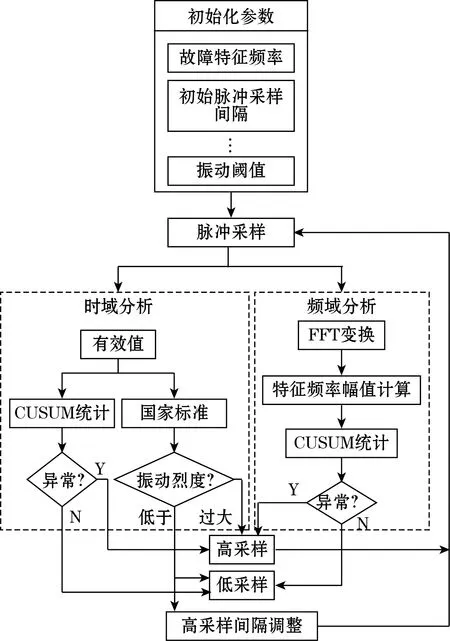
图4 算法流程图

由上可知本文主要的研究内容变成了如何设定时频域特征标准，如何检测特征的变化，以及如何调整脉冲采样间隔等问题。

2.1 时频域分析

频域中，设备高频成分与时域特征值的改变往往伴随低频成分的变化，因此只需通过检测、计算低频的故障特征频率值来指导系统执行变采样。时域中，选取有效值作为振动信号的判定指标来指导变采样。

2.1.1 设备故障特征频率

本文自适应数据采集的研究对象是型号为ZMI480/02(A)的离心式输油泵。该离心泵的额定转速为2 980 r/min，滚动轴承为型号6313，叶片数目为4。其轴承故障频率根据文献[17]公式计算得其低频故障特征频率约20、50、100、150、200、250 Hz。

2.1.2 振动异常判定标准

时域中，同时采用绝对判定标准和相对判定标准来评定设备的运行状态。绝对判定标准通过计算信号有效值，并参考国家标准GB/T 29531—2013(泵的振动测量与评价方法)来设定时域振动报警阈值；而相对判定标准是对同一台设备的同一部位定期进行参数测定，并按时间先后进行比较，以正常状态下的有效值作为原始值进行判定的方法。本文利用突变检测策略对信号的相对变化进行判定，后文会详细介绍。

频域中，主要计算设备低频故障特征频率的值，亦采用相对判定标准来设定阈值，利用突变检测策略来判定特征值的变化。

2.2 突变检测策略

受干扰等因素的影响，当设备由正常至故障状态转变时，会出现实际计算的有效值或特征值在阈值的临界处上下波动的现象，该波动会导致采样率的频繁变化，不易于后续数据的重构与分析。而在非稳定、干扰的环境里检测数据的波动变化，一般采用数学统计方法。

针对上述问题，本文使用了一种基于累积和 (cumulative sum，CUSUM)思想的突变检测策略。其原理如图5所示，时域有效值或频域特征值超出振动初始值k时，此时并不能判定为设备异常，而是对超标量进行累计，当连续的累积值超出设定阈值h时才给出报警，并指导更改采样率。

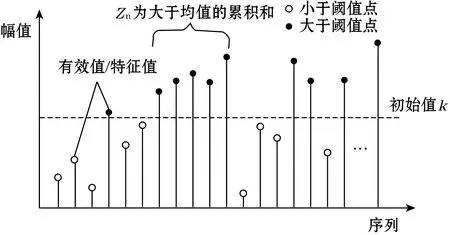
图5 CUSUM模型原理

以下是执行该异常事件检测策略的具体公式与步骤[18]：

给定检测时序x1,x2,…，xn，CUSUM突变检测模型如下：

Zn=(Zn-1+xn-k)+,Z0=0

(1)

式中：“()+”为当x>0时，x+=x，x<0时，x+=0；k为信号的初始值；Zn为xn-k的累积和正值。

若给定报警阈值为h，在时间n发生的变化检测对象异常函数可表示为

(2)

设置延迟时间为d，Zn>0时，说明信号序列发生改变，若Zn≤h，则说明前n-1个统计值没有发生异常，且d=d+1；Zn>h则说明信号在时域中发生改变，即一个突变事件被检测出来，且d=0。

2.3 自适应脉冲采样

2个脉冲采样之间的时间间隔被称为脉冲采样间隔Ta。为进一步强化变采样的“自适应”功能，脉冲采样间隔Ta应是一个可根据当前信号的波动程度而自适应调整的变量，即若当前设备运行平稳，则可适当增大脉冲采样间隔，以实现进一步减少数据的目的。反之，则需减小脉冲采样间隔。

本文基于加性增加乘性减小(AIMD)算法[19]的思想来调整Ta的值，AIMD算法数学公式如下：

I：Ta(n+1)←Ta(n)+α，α>0

(3)

D：Ta(n+1)←Ta(n)×β，1>β>0

(4)

式中：I式为在一个变采样周期内数据波动较小时Ta值的增加算法；α为加性增加的参数值；D式为采集系统遇到数据波动较大时Ta值的减小算法；β为乘性减小的参数值。

本文通过前节计算时域有效值的增量累积和Zn来判定数据的波动情况。设定波动阈值为λ(λλ则表明当前数据不稳定，波动较大，从而能指导系统自适应调整Ta的值。

2.4 信号重构

执行自适应变采样算法后，数据库中储存了高采样率与低采样率混合的同源异构数据，为了便于数据分析与设备故障诊断，需要对降采样的数据进行重构，在保证重构原始信息的情况下，使低采样后的数据量重建为高采样的数据量。

采用插值方法对数据进行恢复，插值是确定某个函数在2个采样值之间的数值时的计算过程。本文采用Sinc插值函数对降采样的数据进行恢复，Sinc插值方法是对己满足采样定理的数据作加密采样点处理，是一种确定性的插值方法。

设x(nΔt)为抽样后的值，x(mδt)为待恢复时刻的值，m为插值的序列标号，其中δt为原始信号的采样间隔，则可设Δt=Lδt，m=n0L+j(n0=0,1,…,L-1)，其中n0为原始数据的序列标号，且k=n0-n插值公式如下[20]：

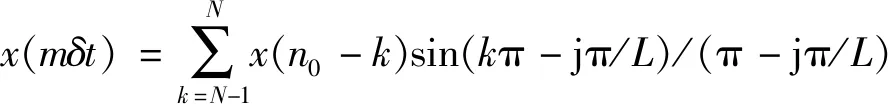
(5)

上式表明，利用抽样后的信号和sinc函数有限离散项可根据nΔt时刻的值恢复mδt时刻的值。

3 仿真设置与结果分析

本文基于MATlAB平台对所设计的自适应变采样算法进行了编程实现。以离心泵设备为研究对象，取某台离心泵在半年时间里从正常运转状态到发生故障的振动信号对该算法进行仿真实验验证。

3.1 参数设置

根据经典AIMD来设定加性因子α与乘性因子β的值，根据多次实验结果来调整波动阈值λ与报警阈值h，阈值优化问题不再详细介绍，具体如表1所示。

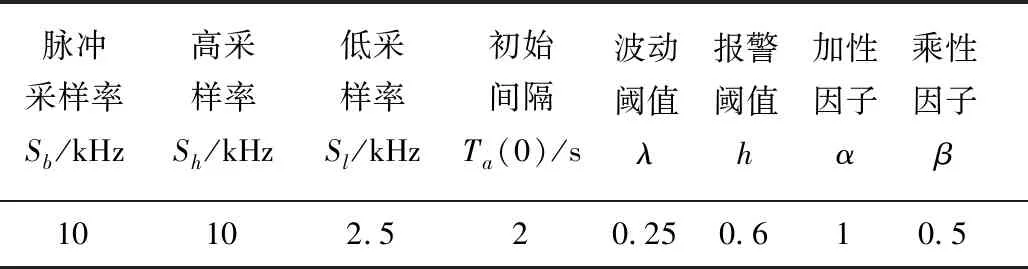
表1 参数设置

3.2 结果分析

3.2.1 自适应采集功能

为了验证该算法的自适应采集功能，现取离心泵正常与故障下的2组振动信号进行仿真实验，仿真结果如图6～图9所示。

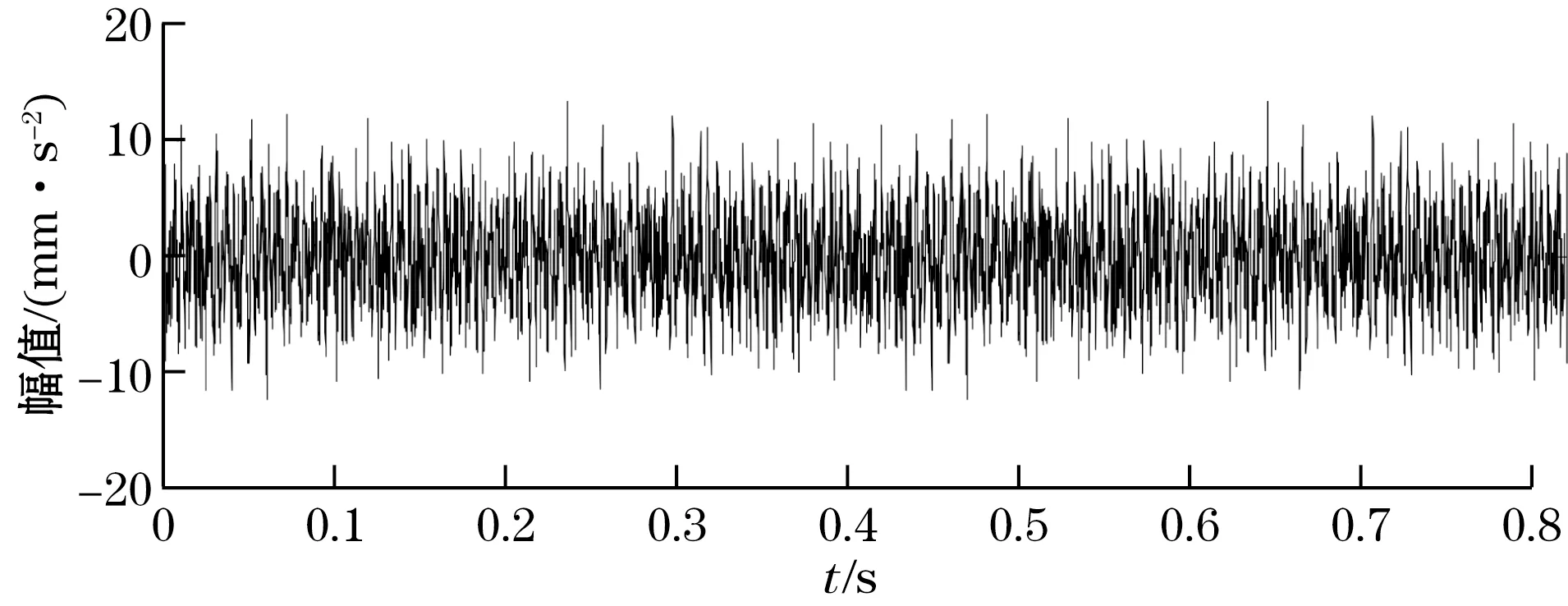
图6 原始正常信号

图7 抽样后的正常信号

图8 原始故障信号

图9 抽样后的故障信号

图6为原始正常信号的时域图，图7为抽样后信号的时域图，可以看出抽样后的波形图略微改变，数据密度减小，说明该算法对正常数据具有自适应降低采样率的功能。图8为原始故障信号的时域图，图9为抽样后故障信号的时域图，可以看出抽样后的波形与数据密度没有发生任何改变，说明当设备发生故障时，该算法自适应地设定了最大采样率。从而验证了该算法的自适应变采样功能。

另取4组离心泵正常状态下的信号，计算其降采样后的时域有效值，计算结果如图10所示，由图10数值比较可知，抽样后与原始信号的有效值基本相等，即抽样后的信号能表征设备运行状态，保留了有效信息。

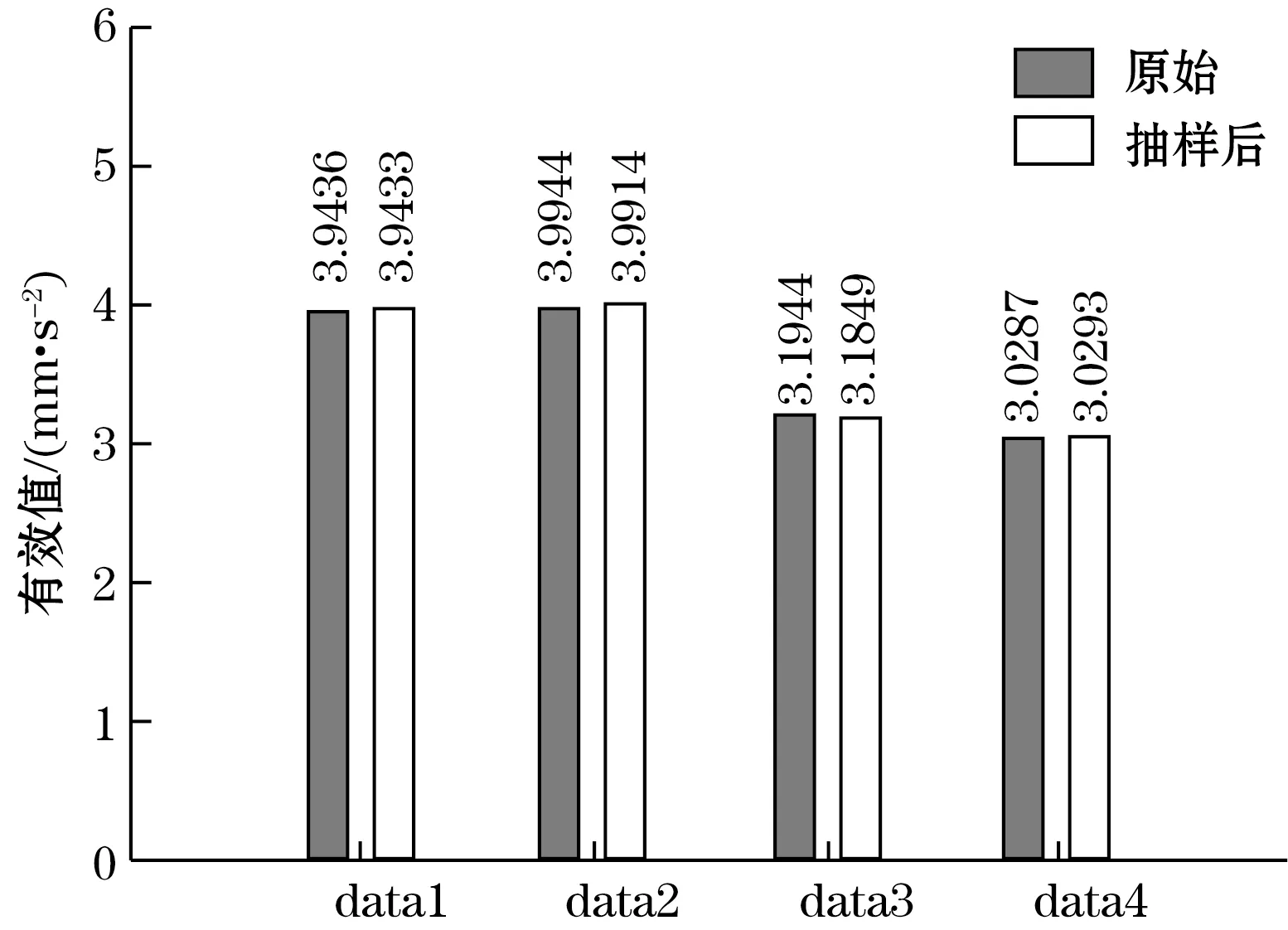
图10 抽样后的有效值

3.2.2 数据重构

为了验证数据重构的准确性，本文对4组离心泵正常状态下抽样后的信号进行了插值重构，其中1组重构与原始信号的时、频域图对比分别如图11与图12和图13与图14所示，从图11、图12可以看出，重构后波形图密度与原始信号密度相当，波形变化不大。从图13、图14可知，与原始信号相比，重构后的信号在低频带基本无损失，只是在高频带丢失信息。但在设备正常运转状态下，只需通过检测、计算低频的故障特征频率值来指导采样率，并不关心高频成分，即可以通过设置低采样率获取设备正常运行状态的信息。

图11 原始正常信号

图12 重构的正常信号

图13 原始正常信号

图14 重构的正常信号

计算4组重构信号1 kHz以内频带的通频值与原始信号对比如图15所示，由图中数值比较可知，重构后信号的低频通频值与原始信号相比差别很小，进一步定量地验证了低频信息无损的结论。

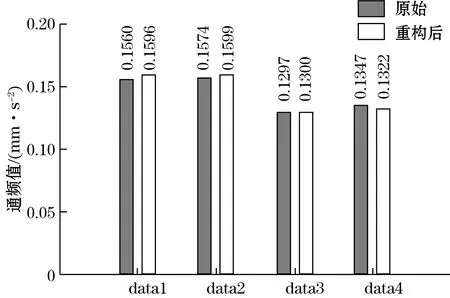
图15 重构后信号的通频值

4 结论

本文提出了机械设备振动信号监测的自适应变采样算法，具体成果与结论如下：

(1)基于累积和(CUSUM)思想设计了一种突变检测策略对振动信号的变化进行判定。

(2)基于加性增加乘性减小(AIMD)算法模型实现对脉冲采样间隔的自适应调整。

(3)实现了采集系统针对设备的运行状态而自适应调整采样率的功能。

本文设计的算法具有对故障信号敏感的优点，解决了数据量与数据有效性之间的矛盾，能极大减小数据冗余，对缓解存储资源压力、降低系统能耗具有重要意义。