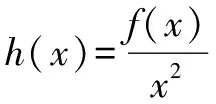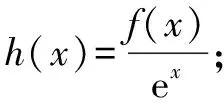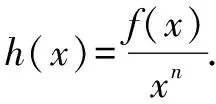不等式中见“真谛” 构造函数导航向
王兰灵
(广东省广州大学附属中学 510006)
在高考或各种模拟考试中,经常会出现关于抽象函数和其导函数的不等式,这类题目往往对学生造成困惑,很多学生遇到之后无从下手.其实,这类题目的条件或者问题中通常隐含着一些隐含的信息,给我们以推理的启示.我们可以顺着启示的方向大胆地猜想、构造辅助函数尝试寻求破解之法.牛顿曾经说过:“没有大胆的猜想,就作不出大胆的发现.”猜想是培养学生创造性思维的有效途径,我们在教学过程中应当注重鼓励学生积极地去观察,大胆地去猜想,引导他们亲身经历从观察、猜想到验证、结论的学习探究过程,由此培养学生的探究能力和逻辑推理能力,提升其数学核心素养.
一、逆用和差函数的导数运算法则构造函数
例1 设函数f(x)在R上存在导函数f′(x),∀x∈R,有f(x)+f(-x)=x2,在(0,+∞)上f′(x) 点评本题的精华是观察、猜想和尝试.只有认真地观察,大胆地猜想,努力地尝试才会发现惊喜. 例2设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有3f(x)+xf′(x)>0,则不等式(x+2015)3f(x+2015)+27f(-3)>0的解集是____. 分析本题有两个思路激发点.第一个激发点为:3f(x)+xf′(x)>0.看到条件“3f(x)+xf′(x)>0”,我们可以猜想构造函数h(x)=x3f(x).第二个激发点是:(x+2015)3f(x+2015)+27f(-3)>0,关注到式子中的(x+2015)3f(x+2015),我们也可以猜想构造函数h(x)=x3f(x),进而验证思路的正确性. 解析因为函数f(x)是定义在(-∞,0)上的可导函数,所以x+2015<0,x<-2015.由3f(x)+xf′(x)>0两边同时乘以x2得:x3f′(x)+3x2f(x)>0,构造h(x)=x3f(x),所以h′(x)=x3f′(x)+3x2f(x)>0,得h(x)在(-∞,0)上单调递增.(x+2015)3f(x+2015)+27f(-3)>0⟺(x+2015)3f(x+2015)>-27f(-3)⟺f(x+2015)>h(-3),故x+2015>-3,得x>-2018. 综上得解集是(-2018,-2015). 点评知识是思路的基础,猜想、尝试和推理是解题的方法.我们既要对导数的运算法则熟悉于心,对函数的构造形式理解掌握到位,又要敏锐观察,大胆猜想,勇于推理尝试,方可寻得解题思路.如本例中看到条件“3f(x)+xf′(x)>0”就猜想构造函数h(x)=x3f(x),或者发现了问题中的(x+2015)3f(x+2015),也尝试构造函数h(x)=x3f(x). 例3(黄冈市2016年高三3月质检)定义在区间(0,+∞)上的函数f(x)使不等式2f(x) 分析题目给的条件很少,由条件“2f(x) 在解有关原函数和导函数的抽象不等式时,学生不但要有发现“真谛”的眼光(具有构造函数的知识储备),更要具有利用函数的重要性质(单调性、奇偶性等)进行严谨推理的能力.在知识储备方面,学生需要对导函数的运算法则熟记于心,不但能正向记忆,更要会逆向运用.函数的构造,本质上是导数运算法则的逆用.因为导函数的运算法则主要涉及和差、积、商三类,所以常见的函数构造形式通常有以下三类. 1.逆用和、差函数的导数运算法则的构造 对于f′(x)±g′(x)>0或f′(x)±g′(x)<0,构造h(x)=f(x)±g(x). 2.逆用积函数的导数运算法则的构造(关系为“加”型) (1)对于f′(x)+f(x)>0,两边同乘ex得:exf′(x)+exf(x)>0,构造h(x)=exf(x); (2)对于xf′(x)+f(x)>0,构造h(x)=xf(x); (3)对于xf′(x)+nf(x)>0,若x≠0,则两边同时乘以xn-1得:xnf′(x)+nxn-1f(x)>0或者xnf′(x)+nxn-1f(x)<0,构造h(x)=xnf(x). 3.逆用商函数的导数运算法则的构造(关系为“减”型)
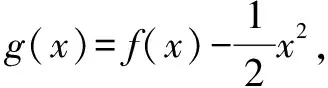
二、逆用积函数的导数运算法则构造函数
三、逆用商函数的导数运算法则构造函数