盾构土压平衡动态神经网络逆控制技术研究

邹今检

(中国铁建重工集团有限公司， 湖南 长沙 410100)

0 引言

土压平衡盾构作为一种专用设备广泛地应用于隧道施工建设。面对复杂多变的地质情况，盾构设备操作不当极易造成地表隆起或坍塌，轻则影响周围地质稳定性，重则造成建筑物的倾斜倒塌甚至人员伤亡。密封舱土压平衡是地表沉降控制的关键因素之一，实现密封舱土压的快速精确控制对盾构安全施工具有重要保障[1-2]。

针对密封舱土压产生的机制模型，胡国良等[3]采用比例压力流量与电反馈复合控制转速从而实现密封舱土压在设定范围内变化； YANG Huayong等[4]采用PID控制器控制密封舱土压变化，通过Matlab仿真与实验结果分析验证该控制方案能够保证密封舱土压在可接受精度下达到预期值； 王林涛等[5]在原有密封舱压力反馈基础上，在推进速度处添加前馈环节，使螺旋输送机马达转速响应时间由2.5 s降为0.5 s，土压控制最大相对误差由6.52%降为1.54%。由于施工中的不确定性以及各掘进参数之间的非线性耦合，密封舱土压难以用理想的土压产生机制表述,为此一些学者开展了土压平衡的非精确模型控制方法的研究。Yeh I. C.[6]采用BP神经网络对螺旋输送机的转速以及液压缸的推进速度进行最优求解，但建模时没有考虑地质条件的影响； Benardos A. G.等[7]采用人工神经网络，基于特定施工现场构建能够进行精确预估推进速度的控制模型； 施虎等[8]建立了以推力、土舱压力、推进速度为输入，以螺旋输送机转速为输出的自适应模糊神经网络土压平衡控制模型，结果表明此模型能够对掘进参数进行有效预测； 李守巨等[9]和上官子昌等[10]等建立了一种考虑盾体与土体耦合作用的密封舱压力控制模型，提出密封舱压力优化控制算法，并验证了该方法的有效性和精确性； 宋英莉等[11]采用IMNMSSPC算法实现密封舱多点土压平衡控制，通过多步预测优化求解螺旋输送机转速与推进速度。

尽管国内外学者对土压控制方法进行了广泛的研究，但现有控制模型多是基于理想土压产生机制亦或基于非线性的静态控制方法。由于盾构螺旋输送机转速控制属于大惯量控制系统，普通密封舱土压闭环PID螺旋输送机转速控制模型对掘进环境的变化难以及时应对。本文采用动态神经网络逆控制器作为螺旋输送机转速的前馈输入，利用现场掘进施工数据进行动态神经网络参数辨识，通过与现场数据的对比分析，验证该控制方法的有效性,以期为土压平衡盾构的土舱压力控制提供一些参考。

1 土压平衡原理及控制系统设计

1.1 盾构土压平衡原理

图1为土压平衡盾构的工作原理示意图。在盾构掘进过程中，刀盘旋转切削产生的土体填充密封舱并不断挤压产生了用以抵消开挖面处地下水压和土压的土浆压力，从而保持开挖面的稳定。由于密封舱内挤压的泥土不断通过螺旋输送机排出盾体，且刀盘转矩与液压缸推力和掘进速度等掘进参数随地质情况不断变化，造成密封舱内土体压力发生复杂变化。在实际盾构施工中，螺旋输送机转速的调节最容易实现，且其他掘进参数难以配合土压平衡随意调整； 因此，本文将刀盘转矩、转速、推进速度作为干扰量输入而不加以控制，将螺旋输送机转速作为输出量，实现掘进参数变化时，通过动态神经网络前馈自动调节螺旋输送机转速和密封舱土压。

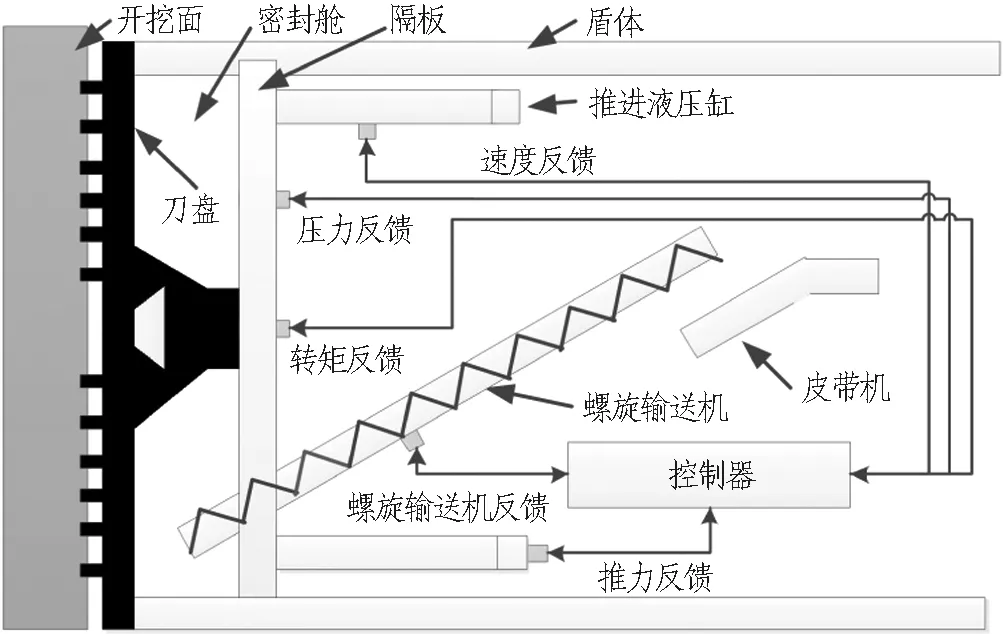
图1 土压平衡盾构工作原理示意图

1.2 土压平衡控制系统

根据上文中的土压平衡原理以及输出执行机构选择，采用如图2所示的螺旋输送机转速控制模型。

根据文献[5]，得到如式(1)所示的螺旋输送机转速调节液压系统的控制数学模型：

nm=Nm(iv,Tl,ps,pa)。

(1)

式中：iv为电磁阀的输入电流；Tl为螺旋输送机负载转矩；ps为螺旋输送机的供油压力；pa为变量泵压力。

螺旋输送机转速反馈系数Gb与控制系统反馈系数Ga分别如式(2)和式(3)所示。

Gb=imaxn/nmax；

(2)

Ga=imaxKpei/iemax。

(3)

式中：imax为电磁阀最大输入电流；nmax为螺旋输送机最大转速；iemax为土压传感器的最大输出电流；Kpei为土压传感器的压力-电流系数(使用过程中换算为压差下的反馈量)。

2 动态神经网络辨识

2.1 动态神经网络

为了减小训练复杂度，本文通过在神经网络中添加时延层方式增强神经网络的动态特性。图3为采用的动态神经网络结构示意图。网络的输入层由外部输入与神经网络的反馈输入2部分组成，输入信号经过时延后进入神经网络的隐藏层。

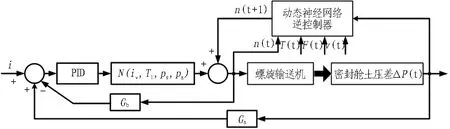
图2 盾构土压平衡动态神经网络逆控制模型

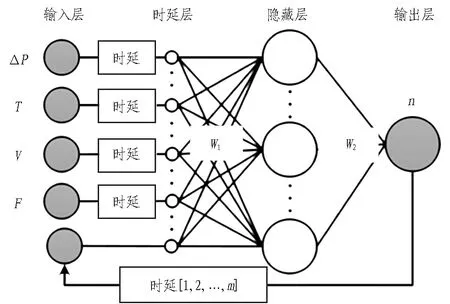
图3 动态神经网络结构示意图

神经网络的下一时刻前馈螺旋输送机转速输出n(t+1)由当前时刻刀盘转矩T(t)、推进速度v(t)、推力F(t)、压差ΔP(t)和转速序列n(t)…n(t-k)等变量的非线性差分方程(式(4))组成。其中ΔP(t)=P(t)-Pe，Pe为期望土舱压力。

根据神经网络前向传递过程，某时刻k下的第j个隐藏点输出Hj(k)如式(5)所示。式(6)为神经网络输出层的输出。

式(5)—(6)中：X=[F,T,v, ΔP]；W1为时延层与隐藏层之间的权值系数；b1为隐藏层的偏置系数；W2为隐藏层与输出层之间的权值系数；b2为输出层的偏置系数；f1、f2分别为隐藏层与输出层的激活函数，这里分别采用双正切函数与线性函数；n为隐藏层节点数目；nx为外部输入量的变量个数；ny为输出量的时延序列数。

当输出值不等于给定的实际值时，神经网络进入反向传播过程。反向传播过程中对各层之间的权值系数进行调整，如式(7)和式(8)所示。

式(7)—(8)中：E为误差目标函数；ns为训练数据的样本数；β为动量阻尼系数；α为学习系数。

本文使用L-M算法求解权值梯度，并采用带动量因子的优化学习算法对权值系数进行更新。

2.2 动态神经网络参数辨识

动态神经网络需要确定延时阶次、隐藏层层数与各层节点数。根据Kolmogorov稳定性，本文神经网络模型选择单层隐藏层。由于神经网络的延时阶次与隐藏层节点数目过少会造成模型精度不够，过大会造成过度拟合，需要根据模型的均方误差适当调整动态神经网络结构。图4示出了动态递归神经网络的参数辨识流程。

1)构建动态神经网络，初始隐藏层节点数；

2)样本数据预处理并归一化；

4)调整神经网络延时阶次，重复步骤3)，计算g=|e(j+1)-e(j)|，使g达到最小；

5)调整神经网络隐藏层节点数，重复步骤3)和步骤4)；

6)训练结束。

2.3 参数辨识结果与分析

根据2.1节中的网络模型，需要辨识的参数为W1(W1_ΔP,W1_F,W1_T,W1_v,W1_n分别表示神经网络输入变量对应的时延层与隐藏层之间的权值系数)，W2，b1和b2。本文采用上海地铁某段盾构施工现场掘进数据； 采用φ6 760 mm级土压平衡盾构，刀盘开口率为40%； 螺旋输送机采用轴式设计，内径为820 mm。隧道主要穿越淤泥质黏土、粉质黏土、中粗砂地层； 隧道埋深为4～40 m。掘进过程中推进速度v=0～65 mm/min，推力F=0～25 000 kN，刀盘转矩T=0～2 762 kN·m，螺旋输送机转速n=0～16 r/min。选择1 000组刀盘转速稳定状态下(1.2 r/min)的采集数据进行训练。训练过程中动态神经网络学习效率为0.1，训练步数为10 000步。

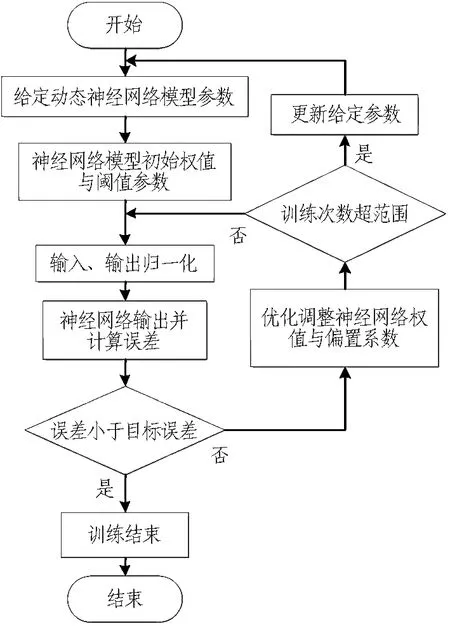
图4 神经网络参数辨识流程

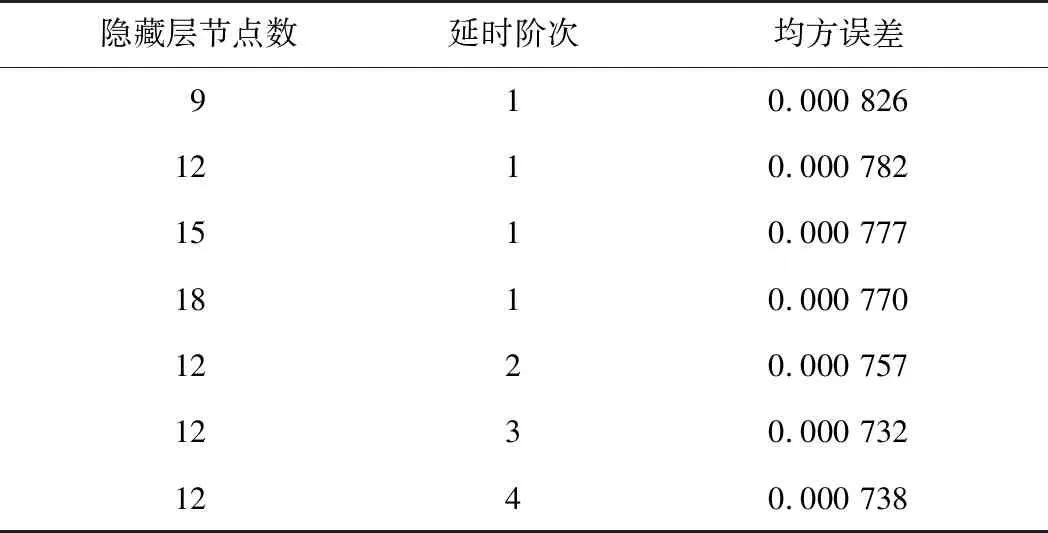
表1为不同隐藏层节点与延时阶次下的均方误差。可以看出： 在隐藏层节点数为9、延时阶次为1与2时，训练的均方误差的相对值(相对延时阶次为4)依次为5.9%和2.57%； 延时阶次为3和延时阶次为4时的误差相接近； 隐藏层节点数在9～18时，模型均方误差均小于0.000 1； 当隐藏层节点数由9增至15时，均方误差的相对误差分别为下降了7.2%、4.5%、2.4%，误差下降幅度不断减小。

表1不同隐藏层节点与延时阶次下的均方误差

Table 1 Mean square errors under different hidden layer nodes and delay orders

隐藏层节点数延时阶次均方误差910.000 8261210.000 7821510.000 7771810.000 7701220.000 7571230.000 7321240.000 738

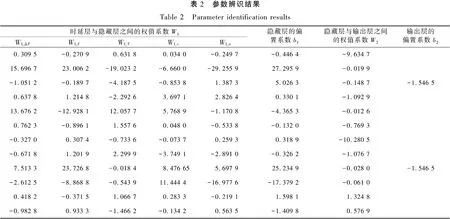
为了减少训练时间，采用延时阶次为1阶、隐藏层节点数为12的动态神经网络结构作为训练采用的网络模型。对现场样本进行训练后辨识得到的模型参数结果如表2所示。

为了验证动态神经网络模型的可靠性，另采用300组现场数据对训练后的动态神经网络模型进行验证，结果如图5所示。可以看出神经网络的预测输出值与实际值变化较为一致。对两者的误差进行统计分析，得到动态神经网络的预测值与实际结果之间的均方误差为0.16，误差的标准差为0.4，表明训练的模型能够较为准确地预测下一时刻的前馈螺旋输送机转速值。

3 动态神经网络逆控制性能分析

3.1 干扰变量斜坡激励

由于本文将土压平衡盾构的推力、推进速度、刀盘转矩等掘进参数视为干扰量，不进行调控。但这些掘进参数的变化将会造成土舱压力的改变，为此本部分初步探究动态神经网络模型对3种干扰变量的响应。

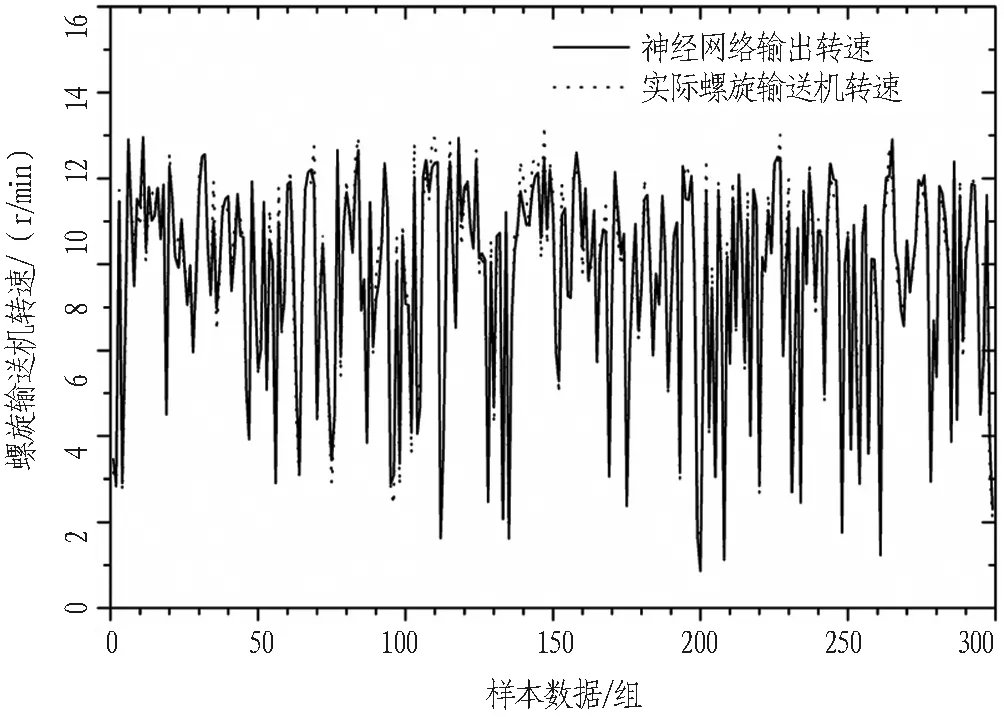
图5 神经网络输出值与实际值比较

Fig. 5 Comparison of output value between neural network and actual value

图6示出3种干扰量斜坡激励下螺旋输送机转速响应情况。激励输入的时间间隔与样本采集间隔相同，均为1 min。扰动变量初始值分别为F0=15 000 kN、T0=1 000 kN·m、v0=10 mm/min； 稳定值分别为Fb=22 000 kN、Tb=2 500 kN·m、vb=60 mm/min。可以看出，对于推进速度、刀盘转矩，在输入变量的斜坡激励下，神经网络的输出近似为相同类型的响应曲线； 但对于推力的斜坡激励，神经网络的输出变化差异不显著。表明动态神经网络对推力作为干扰量输入情况下的前馈效果并不明显； 而推进速度与刀盘转矩的变化将直接影响土舱压力的变化，对螺旋输送机转速调节起关键性的作用。

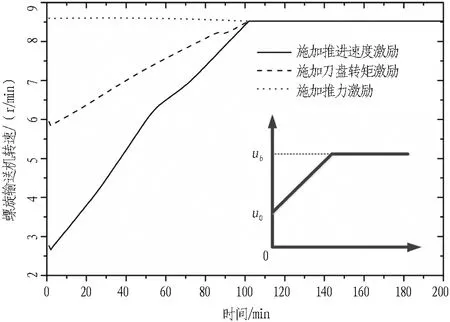
图6 干扰量斜坡激励下螺旋输送机转速响应情况

Fig. 6 Variation of speed of screw conveyor under slope excitation with disturbance variable

3.2 神经网络实际控制效果

为了验证动态神经网络逆控制器前馈作用下土压平衡控制效果，图7给出了刀盘转速在1.2 r/min左右下，动态神经网络逆控制器前馈作用与人工调节下的土舱压力变化情况。由图7可以看出，在运行过程中由于扰动的存在，土舱的压力处于波动状态，但动态神经网络逆控制器前馈作用下的土舱压力波动整体较小。就压力波动的误差大小，人工调节下的土舱压力最大波动误差为9.8%，动态神经网络逆控制器前馈作用下土舱压力的最大波动误差为5.3%，土舱压力的控制精度得到了提高。

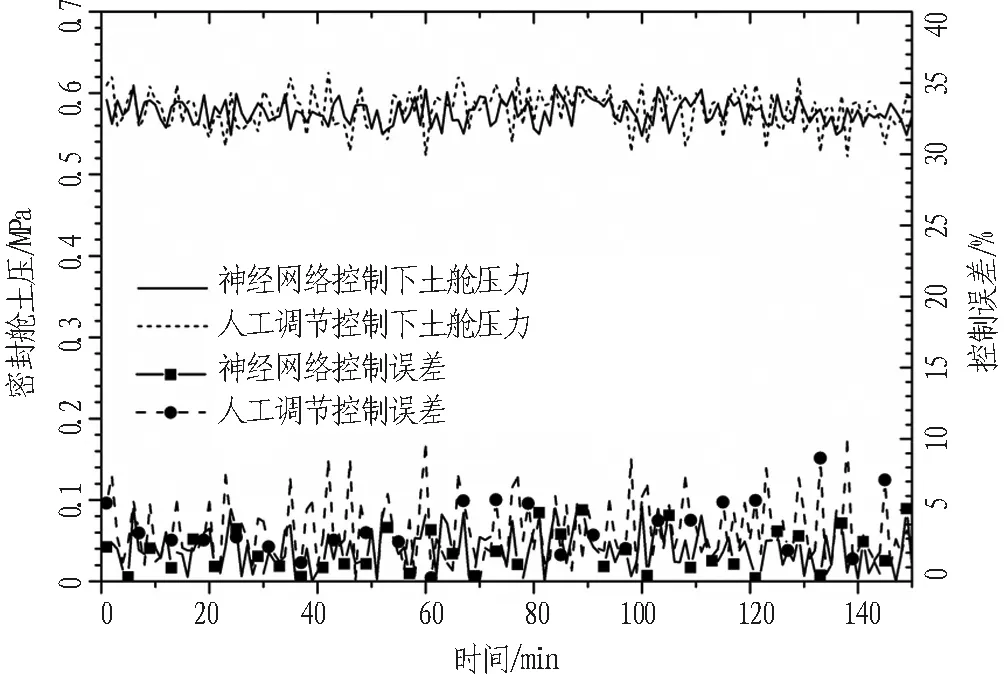
图7 土舱压力随输入信号实时变化情况

Fig. 7 Real-time variation of earth chamber pressure with input signal

4 结论与建议

本文依托上海地铁某段土压平衡盾构施工现场掘进数据，根据盾构施工中对影响密封舱内土压的掘进参数调控的难易程度，采用动态神经网络映射土压平衡中掘进参数之间的非线性耦合关系，根据动态神经网络前馈输出调节螺旋输送机转速以提高土舱压力控制精度，以期为盾构土压平衡螺旋输送机转速控制提供参考。

1)根据施工现场掘进数据训练得到的动态神经网络，可以在一定程度上映射出影响土舱压力的掘进参数之间的非线性关系。

2)通过对训练得到的动态神经网络逆控制器进行不同输入量的斜坡激励，螺旋输送机转速响应结果表明推进速度与刀盘转矩的变化造成的前馈作用显著，而推力变化导致的前馈作用较弱。

3)与现场土舱压力对比，盾构土压平衡动态神经网络逆控制前馈作用下的螺旋输送机转速控制方法能够减小土舱压力波动，密封舱土压波动由9.8%降为5.3%。

4)由于施工现场的复杂性与地质条件的不确定性，建议结合不同的工程实例，进一步完善盾构土压平衡动态神经网络逆控制调节螺旋输送机转速方法。