基于盾构掘进参数的孤石地层识别方法研究

刘建东, 郭京波， 王旭东

(石家庄铁道大学机械工程学院， 河北 石家庄 050043)

0 引言

盾构是集机、电、液、光及信息等多种要素于一体的高科技工程装备，在隧道建设中发挥重要作用。为指导盾构选型及施工，通常在隧道开挖前进行工程地质勘探，但考虑经济因素，无法精确勘测隧道各处的地层状态。在我国华南地区，特别是广州、深圳、珠海等地，盾构施工经常面临上软下硬、孤石等不良地层，依据地质勘探资料无法准确预知其位置、范围及强度。盾构在掘进过程中一旦遭遇孤石地层，常常伴随刀盘被卡、刀具受损、掘进困难及地表沉降等问题，轻则造成经济损失，重则发生人员伤亡，严重危害隧道施工安全。因此，在盾构掘进中准确识别刀盘前方的孤石地层十分必要。

目前，隧道超前地质识别技术，如地质调查、地质雷达、红外探水、超前钻探及加深炮孔等方法在适用范围、识别对象等方面存在差异，各有利弊，单一的超前地质识别方法难以保证精度[1]。

盾构掘进过程中，刀盘前方地质复杂多变。盾构掘进参数是地质情况的外在表现，研究掘进参数有助于准确识别孤石地层。盾构主掘进参数包括刀盘转速、刀盘转矩、总推力、土舱压力、推进速度及螺旋输送机转速等。李正[2]研究了掘进参数在复合地层条件下的变化规律，得到了掘进参数的合理控制范围。徐新等[3]对盾构在软硬不均地质中下穿有地下通道的掘进参数进行优化分析，发现土舱压力对地下通道沉降影响较大，对地表纵向沉降影响较小。邵成猛[4]研究了盾构掘进参数在不同地层条件下的变化规律，提出基于黏土地层的掘进参数神经网络识别方法。赵博剑等[5]采用数理统计分析了盾构主掘进参数与典型地层间的相关性。李俊逸[6]采用数理统计与理论分析的方法对盾构掘进参数进行研究，探明了不同地层下掘进参数的控制范围,得到了各参数间的内在关系。

国内外对盾构掘进地质识别的研究发展较为缓慢，且较多集中在均质地层方面。Laura等[7]基于盾构施工中地下水振动情况与掘进参数及地质特征的相关性，将盾构掘进模型作为描述地质特征的工具，研究了刀盘前方地层状态。Bouayad等[8]提出采用PCA和ANFIS相结合的方法来模拟土压平衡盾构掘进参数及地质情况与地表沉降之间的非线性关系。Hoffmann等[9]研制了一种嵌入式传感器，可准确探测掘进过程中的不明障碍物。文献[10-11]运用模糊识别理论，将比推力及比转矩分为3种状态，并对岩石可切割性进行等级划分，验证了岩石类别划分和可切割性模糊识别方法的可行性。文献[12-13]基于黏土、砂土及砂砾土3种地质的掘进数据，运用神经网络方法研究掘进数据与地质条件的非线性映射关系，实现地层在线识别。李明阳等[14]以Terzaghi松动土压力模型和CSM模型为基础，对土压平衡盾构的掘进表现进行模拟并分析研究了复合地层下盾构的受力情况，结果表明综合考虑软土与硬岩模拟分析结果的掘进参数模拟分析法具有一定有效性。

综上所述，国内外学者对孤石地层与盾构掘进参数间相关性的研究较少，基于从已知掘进参数到识别盾构施工孤石地层的反向思路展开的研究则更少，仅在黏土、砂土及砂砾土等均质地层识别有所关注，缺乏在上软下硬、孤石等地层识别方面的探索。

本文基于盾构掘进比能，结合主掘进参数，研究盾构施工孤石地层SM识别法及识别矩阵；运用BP神经网络技术建立孤石地层神经网络识别模型。利用珠海某盾构区间实测掘进数据进行工程验证，结果表明识别效果良好。结合2种方法进行双重预判，互相验证，对盾构施工中的孤石地层识别有一定指导意义。

1 工程概况

1.1 地质条件

为了研究盾构掘进过程中的孤石地层识别方法，选取珠海横琴隧道进口段——湾仔北站区间左线工程的典型数据进行分析。隧道全长1 237 m，线路左侧临海，地表有较多工厂。洞顶埋深为0～8 m，局部存在中砂、细砂地层；洞身位于粉质黏土层中，局部存在花岗岩；洞底为花岗岩全风化地层，局部存在弱风化花岗岩。区间存在300 m上软下硬、孤石等不良地质。掘进过程中已遭遇孤石，分布较广，无规律。该区段部分工程地质纵断面如图1所示。

图1 隧道左线工程地质纵断面(单位： m)

1.2 盾构主要技术参数

该施工区间采用海瑞克φ8 800 mm土压平衡盾构，刀盘驱动方式为变频电机驱动，主要技术参数如表1所示。

表1 主要技术参数

2 孤石地层修正比能识别方法

盾构在不同地质中施工，其外在表现为掘进参数不同。在施工过程中依据掘进参数变化趋势，反演出盾构掘进的地层情况，及时发现孤石地层，可防止盾构冒进，规避施工风险。由于盾构施工地质情况复杂多变，掘进参数种类繁多，若通过单一掘进参数直接判断前方地质状况，情况复杂，准确性较低，因此从能量法角度出发进行不良地质识别。

2.1 掘进比能

盾构掘进比能SE定义为刀盘完成的机械功除以开挖地层的单位体积材料：

SE=(Wt+Wn)/V=[(T,F),(ω,v)δt]/(πR2vδt)=

(1)

式中：Wt为转矩能，J；Wn为推力能，J；T为刀盘转矩，kN·m；F为总推力，kN；ω为刀盘转速，r/min；v为推进速度，m/s；R为开挖半径，m。当时间元素δt趋向于无穷小，位移线性近似为vδt。分母中，掘进体积被定义为底面半径为R，高度(推进距离)为vδt的圆柱体。

2.2 修正比能

基于掘进比能值，提出盾构修正比能值SM(modulated specific energy)。修正比能定义为土舱压力系数乘以掘进比能与推进速度逻辑函数l(vN)的乘积的自然对数：

SM=Kpln (w×l(vN))+C。

(2)

vN=αvN-1+(1-α)vN。

(4)

式中：SM单位为MPa；w是一个取决于掘进比能SE的中间变量；vN为掘进速度调节函数，N表示数据采集点号；常数C用于使SM曲线回归到某一特定位置，这个位置不是任意位置，而是使SM曲线中的最小值为零的位置；R为开挖半径；e、m均为常数；α为指数滤波系数，用于缓解vN中因盾构司机操作过快而产生的噪声，根据司机对掘进参数调节敏感度而设定；SM中自然对数有助于放大弱信号，从而提高不良地层的阶跃响应。Kp为基于孤石地层引起土舱压力p变化而设置的系数，土舱压力p为被动调节参数，取平均压力值，受地层影响较大，通过式(5)将p与孤石地层可能性关联起来：

Kp=kp+d。

(5)

式中: 参数k由进入孤石地层的土舱压力变化率确定; 参数d为土舱压力变化系数的基准值，MPa。根据已知孤石地层段的掘进数据，对由非孤石地层进入孤石地层的过渡数据进行线性回归分析，确定k值为-0.625，d值为2.1 MPa。

l(vN)是掘进比能SE的补充似然估计函数，代表推进速度检测效率。

参数a决定曲线的过渡宽度，该值的设定取决于孤石地层对掘进速度的宽容度，由于盾构在孤石中的掘进速度控制在20 mm/min以内，故取a值为0.45。参数b决定似然函数概率值分布，根据掘进速度统计直方图(见图2)可知，掘进速度位于3～10 mm/min的数据占总体样本的90%，b的取值应为似然函数与掘进速度小于10 mm/min时直方图交点所对应的横坐标，故b取值为9.7。参数c决定似然函数的基础点，为使掘进速度样本的检测效率大于1，这里取c值为1。

图2 掘进速度统计直方图与似然估计曲线

2.3 孤石地层识别矩阵

盾构施工中，SM值随掘进参数实时变化，而掘进参数反映了地层的变化。因此，SM值体现了盾构掘进过程中地层的变化情况。对于孤石地层，与SM变化曲线的波峰相关，其值大小与孤石体积及强度成正相关。而盾构在软土地层中掘进时，SM值较小，偏置为0。

建立SM值与孤石地层的识别矩阵R，当盾构遭遇孤石地层时值为1，否则值为0。

对盾构掘进过程中孤石地层的范围和强度进行等级划分：SM值越大，掘进难度越大。若SM值为0，表示盾构未遭遇孤石地层，掘进难易程度为容易；若SM值大于0且小于1，表示盾构遭遇孤石地层，但范围小、强度低，易被切削为岩石碎片随渣土排出，掘进难易程度为普通； 若SM值大于等于1且小于1.5，表示盾构遭遇孤石地质，范围较大、强度较高，掘进难易程度为中等； 当SM值大于等于1.5，表示遭遇孤石地质，且范围大、强度高，盾构刀盘直接切削岩石较为困难，掘进缓慢，若强行推进将严重磨损刀具，掘进难易程度为困难，需采取冲孔桩法、静态爆破法等措施对岩石进行破碎，保证施工安全。

3 孤石地层神经网络识别方法

3.1 基于MATLAB的BP神经网络识别模型

采用newff函数建立BP神经网络识别模型：

net = newff(P,Q,S,TF,BTF)。

(8)

式中：P为输入样本，Q为输出样本，S为隐含层神经元个数，TF为传递函数，BTF为训练函数。

选用双隐含层BP神经网络，隐含层节点数分别为9、2个。根据神经网络识别精度，选择层与层之间的传递函数为tansig和purelin。对比各个训练函数综合效果，选取trainbfg作为训练函数。此外，输入样本为6个主要掘进参数，分别为刀盘转矩T、刀盘转速ω、总推力F、土舱压力p、推进速度v、螺旋输送机转速n； 输出样本为修正比能SM值和孤石地层识别结果。设置网络内部参数学习速率为0.1，误差精度为0.001，训练步长为5 000，其余参数设置为缺省值。

3.2 识别模型训练

以107—114环间已探明孤石地层区域的掘进数据为训练样本进行训练。BP神经网络在建立模型时将训练样本分为3部分，训练集、测试集和验证集。若训练集达到精度要求则停止训练；若验证集在多次验证后梯度改变较小，也会终止训练；测试集体现了实际识别效果。如图3所示，利用MATLAB软件，经反复学习与训练，最终确定孤石地层神经网络识别模型。网络误差为9.8×10-4，满足精度要求。盾构在107—114环间的部分掘进数据如表2所示。

图3 神经网络训练过程

表2 107—114环部分掘进数据

如图4所示，将训练样本作为评价样本来分析BP神经网络模型可靠性，即把训练样本作为测试数据判别孤石地层。

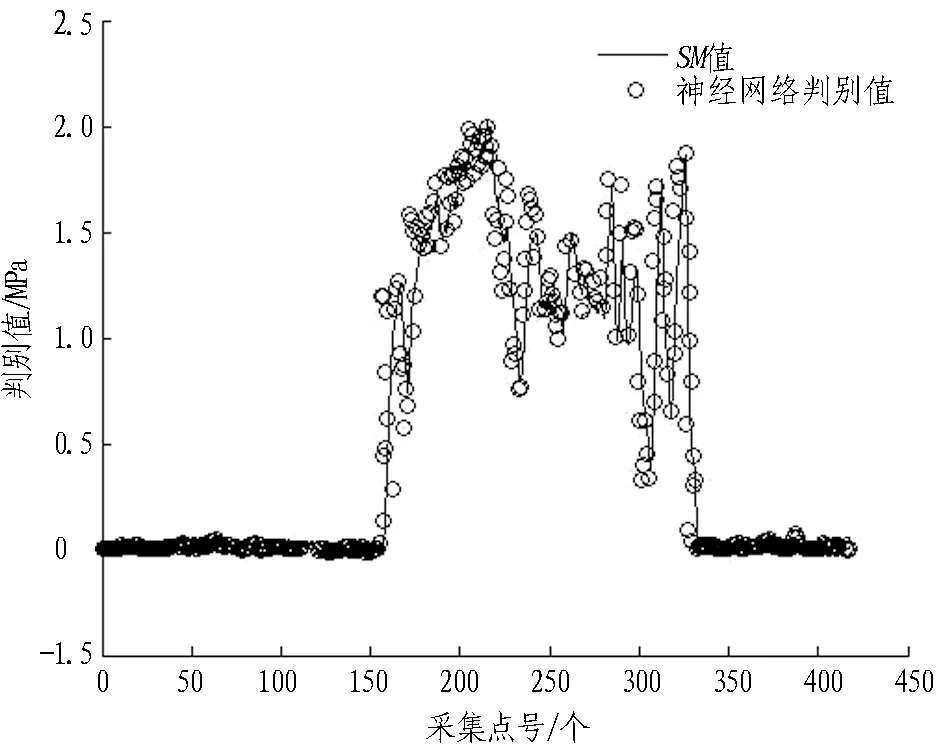
(a) 修正比能值对比

(b) 孤石地层识别对比

Fig. 4 Comparison between predicted results of training sample andSMmethod

结果显示，神经网络判别值与SM值基本吻合，仅存在个别差异点，但误差不大；将识别是否存在孤石地层结果与SM识别矩阵对比，基本相同，且精度非常高。表明该神经网络模型对自身样本的识别精度很高，满足设计要求。

4 实例验证与分析讨论

4.1 孤石地层修正比能识别法

选取该盾构施工区间的3组实测数据对用SM值识别孤石地层法进行实例验证。第1组为107—114环掘进数据，第2组为149—155环掘进数据，第3组为225—231环掘进数据，共计22环数据，采集间隔为60 s。根据详细地勘图，已知第1组地质中111—112环为孤石地层，第2组与第3组为未探明孤石地层数据。

首先，分析已探明孤石地层数据。除去第1组数据中因盾构故障或拼装管片时的停机数据，将其带入识别模型得到SM值曲线，如图5所示。从图5中可以看出，当盾构掘进至157点时，SM值明显上涨，逐渐达到1.56，随着盾构的推进，SM值不断增加，峰值为2.32，后续有所减小但仍持续波动，直至333点时，SM值降低为0。持续观察该区间螺旋机出渣情况，有明显石块夹杂其中的情况，石块直径大小不一，且有石块与螺旋机撞击的声音。

图5 107—114环SM曲线

结合已知地质勘探图与该区间段的SM值，建立107—114环孤石地层的识别矩阵，部分数据如表3所示。综上分析，该区间段内，识别模型效果明显，与地勘图所述孤石位置相符。

表3107—114环孤石地层识别矩阵部分数据

Table 3 Partial data of identification matrix of boulder geology from ring 107 to 114

环号SM值/MPa是否为孤石地层10700108001090011000110001110.4101111.1311111.4211122.3211121.7911120.671

其次，分析未探明孤石地层数据。将第2组数据与第3组数据去除因盾构故障或拼装管片的停机数据，带入识别模型得到SM曲线，如图6所示。

图6 修正比能值变化

如图7所示，149—155环间，盾构推进速度波动较大。当继续掘进至204点，SM值突变，最大值为1.39，持续时间为31 min，判断此区间存在较大范围孤石地质，掘进难易程度为中等。此段推进速度平均值为4.36 mm/min，土舱压力降低至1 MPa。如图8所示，在螺旋输送机口明显观察到岩石碎片，据此判断该位置SM值突变与遭遇孤石地层有关。该区间孤石地层识别效果明显，仅出现几个偏差数据点，在后续掘进过程中得到及时纠正，SM模型具有良好的稳定性和容错能力。

图7 149—155环掘进参数变化

如图9所示，225—231环间，掘进参数整体较为平稳，推进速度无较大波动。225环开始，推进速度逐渐减小，土舱压力逐渐降低，掘进至66点时，SM值逐渐增大，最大为1.27。调整掘进参数继续推进，SM值逐渐下降后又上升至0.95，之后无突变。据此判断该时段存在孤石地层，范围较小，正常掘进即可顺利切削岩石。区间内推进速度平均值为11.16 mm/min，土舱压力降低至1.57 MPa。后续观察螺旋输送机出渣情况，渣土中混有小直径岩石碎片，表明识别效果良好，SM值与孤石地层中的岩石直径及强度相关。

图8 岩石碎片

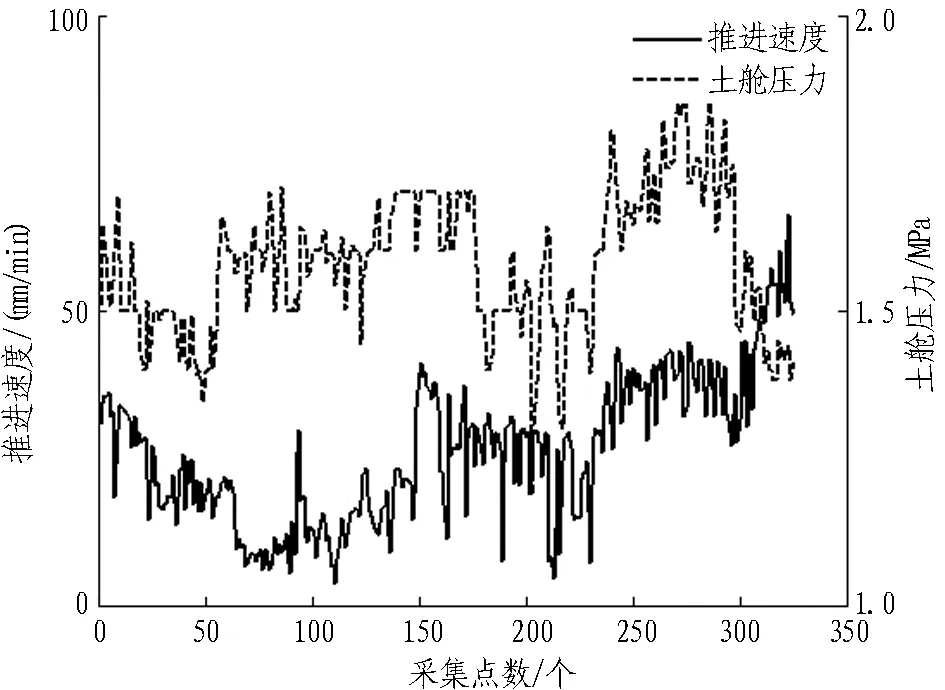
图9 225—231环掘进参数变化

4.2 掘进比能与修正比能识别效果对比

已探明111—112环间存在孤石地层。采集107—114环盾构掘进数据，去除盾构故障及拼装管片的停机数据。采集间隔为60 s。分别用掘进比能法和修正比能法识别孤石地层，结果如图10所示。

图10 掘进比能法与修正比能法对比

分析可知，孤石地层下的掘进比能值明显大于非孤石地层，掘进比能与地层状态有较强相关性；掘进比能特异性较低。如图11所示，在120～130点，由于盾构司机操作引起推进速度变化剧烈，该时段掘进比能同样存在较大波动。此外，掘进比能变化曲线的基线不为0。因此，通过掘进比能无法准确识别孤石地层所在的区域。SM模型的识别效果良好，SM值直接反映了地质状态，结合孤石地层识别矩阵，可判明孤石地层的范围与强度，可为盾构司机调整掘进参数提供一定参考，有一定的合理性与适用性。

4.3 孤石地层神经网络判别法

以149—155环、225—231环掘进数据为神经网络模型的测试样本，用sim函数调用保存过的识别模型，将识别结果与SM值及识别矩阵作对比，输出结果如图12所示。

图11推进速度

Fig. 11 Advancing speed

(a) 149—155环修正比能值对比

(b) 149—155环孤石地层识别对比

(c) 225—231环修正比能值对比

(d) 225—231环孤石地层识别对比

图12神经网络法与修正比能法对比

Fig. 12 Comparison between neural network method andSMmethod

神经网络法对SM值的判别效果良好，其判别值与SM计算值基本相同，变化趋势一致。149—155环的孤石地层判定结果与SM识别矩阵对比，存在5个偏差点，吻合率为98.3%； 225—231环有1个误判点，3个偏差点，正确率为98.8%，满足精度要求。神经网络模型对盾构掘进数据有很强的泛化能力，利用神经网络法识别刀盘前方孤石地层的方法可行。

5 结论与建议

基于盾构主掘进参数，结合掘进比能，提出盾构修正比能，建立孤石地质识别模型及识别矩阵，同时运用BP神经网络技术，以施工实测数据为训练样本建立神经网络识别模型，通过工程验证，得到主要结论如下：

1)修正比能法具有很好的容错性、稳定性及特异性，结合孤石地质识别矩阵，可判明孤石地质的范围与强度，相对于之前的掘进比能法识别效果更佳；神经网络判别法对孤石地质的判定结果与识别矩阵基本相同，2组实测数据下的吻合率为98.3%和98.8%，精度较高。

2)基于盾构主掘进参数的修正比能法，结合神经网络法进行参考验证，切实可行，为盾构司机调整掘进参数提供参考，尽量避免施工事故，具有较好的工程实际意义。

3)本文提出的孤石地层识别方法，仅对珠海横琴隧道进口段——湾仔北站区间所用φ8 800 mm土压平衡盾构进行验证。后续研究应针对不同刀具布置形式、刀具类型及开挖直径进一步验证其准确性与可靠性，从而形成更为有效的识别方法。