高压除湿转轮系统性能模拟与分析

严豪，葛天舒，代彦军，王如竹

（上海交通大学制冷与低温工程研究所，上海 200240）

0 引言

近年来，转轮除湿凭借其结构简单紧凑、运行效率高、除湿量大等优势，逐步成为研究焦点，广泛应用于生活和生产中。硅胶作为固体吸附材料具有无毒[1]、相对湿度适用范围广且吸附能力强[2]等特性，市场上的转轮多以其为吸附材料进行制备[3]。

国内外关于除湿转轮的数学模型研究较早。MACLAINE-CROSS等[4]使用比拟法分析了除湿转轮的传热和传质过程，利用对传热过程的求解来分 析预测传质过程。BARBY等[5-6]将硅胶流床的传热系数和传质系数实验关联式应用在HOUGEN等[7]提出的数学模型中，并通过实验的方法研究了硅胶除湿转轮的传热传质过程。ZHENG等[8]使用隐式的有限差分法对转轮的一维传热传质过程进行模拟，并在此基础上进行性能优化。DAI等[9]通过数值计算用参数分析法对除湿转轮的性能进行了详细地分析和讨论。张学军[10]通过对一个一维数学模型的数值计算，分析讨论了运行参数、结构参数对转轮除湿器性能的影响。NIU等[11]通过对一个二维数学模型的数值求解，讨论了干燥剂厚度对除湿转轮传热传质的影响，指出在某一转速下有一定厚度的活性层对于干燥剂而言是参加传热传质活动的必要条件。MIHAJLO等[12]导出了分别适用于非冷凝条件和冷凝条件下的两组控制方程。钟金华[13]模拟研究了高压下不同形状因子对干燥剂吸附性能以及再生区冷凝情况的影响。

采用新型复合材料或者加大系统的工作压力都是提高转轮除湿效率的有效方法[14-15]，本文主要针对后者进行研究。除湿转轮应用于压缩空气干燥时，运行工况由大气压力变为高压，固体干燥剂的吸附和解吸能力将发生改变，在高压工作环境下，转轮的吸附能力得到提升，但同时，再生区域有可能发生凝结现象，降低干燥剂的解吸能力，使除湿效果变差。本文对高压工作环境下转轮的传热传质过程建立了控制方程，并利用数值方法进行模拟分析，讨论了工作压力下各参数对转轮干燥效率（以除湿量和压力下露点为考察标准）的影响，为除湿转轮在压缩空气领域的应用提供理论基础。

1 空压机深度除湿循环

图1所示为高压除湿转轮系统循环。整个转轮处在高压环境下，从空压机出来的气体分离成两股：其中15%的压缩气体作为再生热空气，进入转鼓干燥机再生区，然后通过冷却器；剩余的85%压缩空气经过冷却降温后，与解吸后的再生空气汇总，随后进入转鼓干燥机进行吸附处理，最终排出，以达到整个装置零气耗的效果。

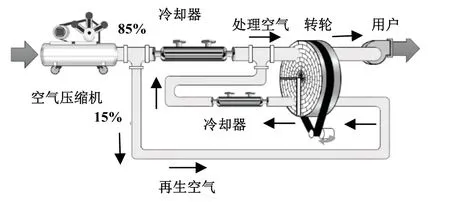
图1 高压除湿转轮系统循环

图2所示为转轮系统。除湿转轮是整个系统的核心，一般由涂有吸附材料（硅胶、分子筛等）的基材料（纸基或陶瓷基）组成，负责对高压空气的除湿处理。转轮两侧由特殊的密封装置分成两个区域：处理区域和再生区域。处理区域中，干燥材料吸附气体中的水分进行除湿；再生区域中，高温空气带走干燥材料中水分对其进行再生。转轮不断转动，以保证除湿系统持续稳定的除湿状态。

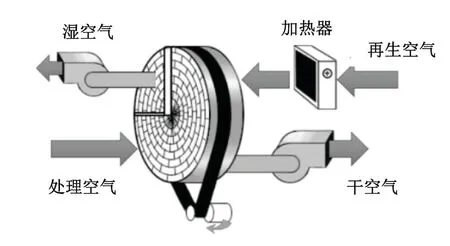
图2 转轮系统

2 系统模型构建

由于本文所研究的是承压工况下的转轮除湿性能，在高压条件下，再生区域的干燥材料可能出现不能完全解吸的情况，此时再生区域会发生冷凝。本文将根据是否发生冷凝来建立模型并进行调节。

2.1 没有冷凝发生时的系统模型

当没有冷凝发生时，系统的控制方程与常压下的相似[16]，对常压下的转轮系统进行模拟。将除湿转轮按照31∶的比例划分为处理区和再生区，并以转轮截面中心为起点，螺旋向外做波纹形通道[17-20]，如图3所示。选取除湿转轮中的某一个气流通道，建立拉格朗日坐标系，在dz内可以采用集总参数法，建立一维传热传质数学模型进行数值求解，如图4所示。

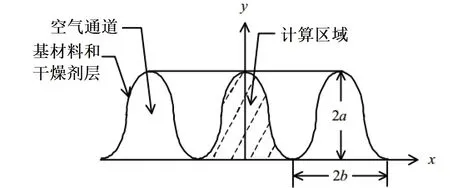
图3 波纹型通道

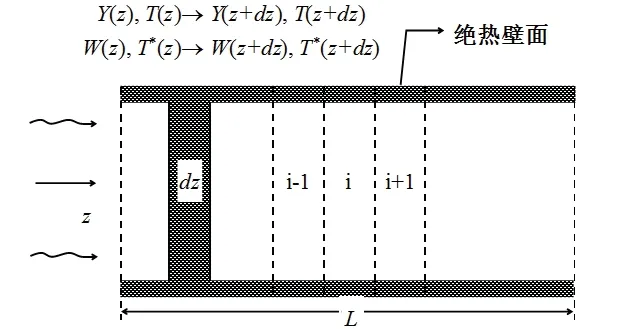
图4 波纹形空气通道内部微元体

没有冷凝发生时，根据质量和能量守恒定律，建立控制方程，并写成时间导数和空间导数向后差分的隐式迎风差分方程[10]，对上述方程采用全主元高斯-约当消元法，通过计算机编程求解[21]。

2.2 冷凝发生时的判定条件与模型调整

采用安东尼饱和水蒸汽压方程判断是否发生冷凝[22]。

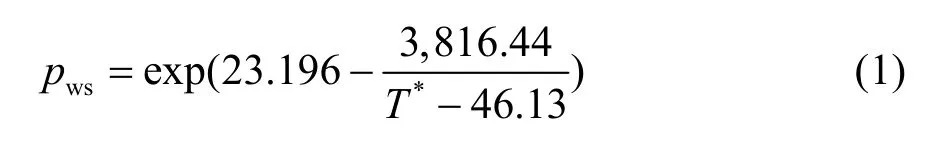
式中：

T*——干燥剂温度，℃；

pw——水蒸气分压力，MPa。

当pw＞pws时，冷凝发生。冷凝发生时，控制方程将进行转变[13]。

2.3 模拟所用的初始工况

假设承压状态下硅胶的吸附率提升30%，模拟计算所采用的参考工况参数条件如表1所示。

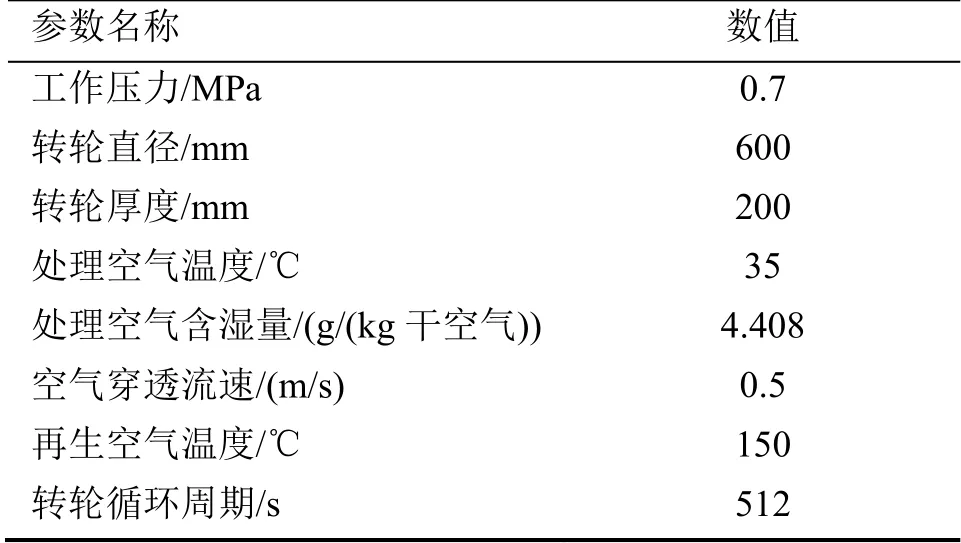
表1 数值计算所采用参数

2.4 承压下空气参数的变化

与常压对比，在承压状态下，空气侧的物性参数将发生变化。查询0.7 MPa压力下空气侧发生变化的参数，如表2所示。

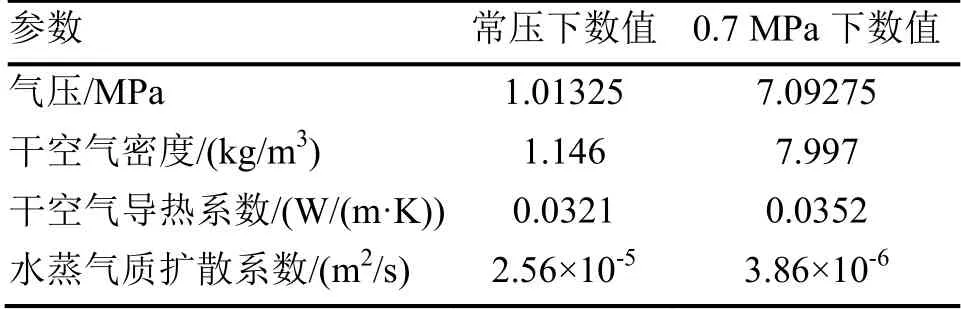
表2 0.7 MPa压力下相对常压的变化参数

3 模拟结果分析

本文采用除湿量D来描述转轮的除湿性能：

式中：

Yp1、Yp2——处理空气的进出口含湿量， g/(kg干空气)。

除湿量D体现了处理空气经过转轮之后，绝对含湿量的变化。D越大，说明转轮的除湿能力越强。

根据建立的数学模型，通过控制变量法改变参数，模拟计算出转轮的除湿量D及0.7 MPa压力下出口处露点温度，并据此评判转轮系统的除湿性能。

3.1 再生温度对系统除湿性能的影响

图5给出了其他参数不变时，再生温度从120 ℃到180 ℃，对转轮系统除湿性能的影响。从模拟结果可以看出，随着再生温度的提高，转轮的除湿量D上升，出口处的空气露点温度逐渐降低，降低幅度呈减缓趋势。再生温度越高，除湿转轮的解吸速率就越快，因此系统的除湿量上升。

图5 再生温度对系统除湿性能的影响

3.2 停留时间对系统除湿性能的影响

停留时间的定义如式（3）所示：

式中：

L——转轮轴向厚度，m；

v——空气流速，m/s。

固定轴向空气流速为0.5 m/s不变，通过改变转轮厚度来控制空气在转轮内部停留的时间长短。图6所示为停留时间对系统除湿性能的影响，空气在转轮内停留时间越长，吸附越充分，露点温度越低，但当厚度到达到一定值时，由于空气干燥得足够充分，继续加厚所带来的除湿量提升逐渐趋于零。

固定转轮厚度为200 mm不变，改变轴向空气穿透速度，并分析其对转轮系统的除湿性能的影响。如图7所示，随着穿透速度的不断提高，处理气体在转轮中停留的时间越来越短，除湿效果越来越弱。但是，降低流速到达一定程度后，对除湿效果的提升不明显，并且过低的流速可能导致转轮系统不满足流量的要求，因此适当降低流速可以提高转轮的除湿性能。

图6 固定流速时停留时间对系统除湿性能的影响

图7 固定厚度时停留时间对系统除湿性能的影响

3.3 吸附时间对系统除湿性能的影响

吸附时间是指转轮吸附区初始的一个微元转过整个吸附区所需的时间，占转轮转动周期的四分之三，与转速有直接关系。

改变吸附时间对系统除湿性能的影响如图8所示，图中给出了出口端空气的露点温度与吸附时间的关系。可以发现，除湿转轮存在一个最优转速使系统能获得最大的除湿量。露点温度随着吸附时间的升高呈先下降后上升的趋势，在150 s左右存在一个最优值使除湿量最大，表明在此条件下的最优周期为200 s，即18 r/h的转速有利于提高转轮的吸附性。

3.4 转轮直径对系统除湿性能的影响

转轮直径也是系统除湿效率的因素之一。提升转轮的直径可以让入口空气的接触面积增大，使除湿效果更好，但同时要考虑经济和空间的限制。图9所示为转轮直径对系统除湿性能的影响，随着转轮直径的增加，按比例提高单位长度基材料和干燥剂的质量。可以看出，随着转轮直径的增加，系统除湿量D逐渐上升，出口气体的露点温度呈现下降趋势，并且这种趋势在800 mm之后有所减缓。

图8 吸附时间对系统除湿性能的影响

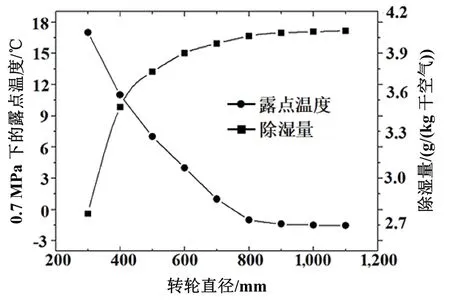
图9 转轮直径对系统除湿性能的影响

3.5 优化参数选取

通过上述比较分析，对转轮参数的优化选取如表3所示。

表3 转轮优化参数选择

4 结论

本文建立了高压下转轮除湿系统的数学模型，并通过模型模拟计算，分析了各种参数对转轮系统除湿性能的影响，得出如下结论：

1）适当提高再生温度能够提升转轮的除湿性能；

2）加大空气在转轮中的停留时间有利于提高系统除湿性能；

3）存在最优转速，使转轮的除湿效果最好；

4）在空间和经济条件允许下，适当加大转轮截面积也能提升转轮的干燥性能；

5）以表3所示参数进行模拟，最终出口处可以达到0.7 MPa压力下露点温度为-5 ℃。

本文模拟分析了各参数对承压状态下转轮除湿性能的影响，并对参数进行优化选取，为今后承压除湿转轮实验台的建立以及除湿转轮在压缩空气领域的应用提供了初步的理论基础。