解释水平对小学生数感发展的影响

洪超 孔冬梅

摘 要：近年来，数学课程改革将发展数感列为重要议题。对于数感的培养，众多学者认为，要让学生掌握数学问题的本质，对抽象的数学知识具体化、形象化。解释水平反映了个体对事物抽象表征水平的倾向，对需要掌握抽象的数学知识的本质这种数感能力可能产生影响。因此，本研究采用解释水平问卷和小学生数感问卷对涪陵城区第十三小学4-6年级260名学生进行调查研究。结果显示：1.小学生的解释水平存在明显差异，女生的解释水平比男生高。2.解释水平显著影响小学生的数感水平，其26.9%的变化都是由解释水平所引起的。

关键词：数感;解释水平;教学;小学生

The Influence of Constual Level on the Development of Primary School Students' Number Sense

Chao Hong1，Dongmei Kong2

（1.South Sichuan Preschool Education College，Longchang 642150，China;

2.Nan'an Jiangnan Shui'an Primary School of Chongqing 401336，China）

Abstract：In recent years，the mathematics curriculum reform has listed the development of the number sense as an important issue.For the cultivation of the number sense，many scholars believe that it is necessary to let students grasp the essence of mathematical problems and to make concrete and visualized the abstract mathematical knowledge.The constual level reflects the individual's tendency to abstract the level of representation of things，and may have an impact on the ability to grasp the essence of abstract mathematical knowledge.Therefore，this study used the constual level questionnaire and the Primary School Number Sense Questionnaire to investigate  260 students in grades 4-6 of the 13th Primary School in Fuling City.The results show that：1.There is a significant difference in the constual level of primary school students.The constual level of girls is higher than that of male students.2.Constual level significantly affects the number sense of primary school students，and the 26.9% change in the number sense is caused by constual level.

Key words：Number sense;Constual level;Teaching;Primary school students

1 問题提出

数感是对数字关系和数字模式的意识，以及运用这种意识灵活解决数学问题的能力，是个体认知数学对象进而成为数学气质的心智技能。数感是个体对数学知识在头脑中的认知图式（潘星宇，俞清怡，苏彦捷，2009），数感的发展不仅受内在生理和认知水平发展的影响，而且还受到社会环境的影响。因此，对于数感的培养，众多学者认为，要让学生掌握数学问题的本质，教学过程中，要结合学生的生活实际、关心的事物，要提供给学生丰富而具体的支持环境/事物（夏云川和曹晓君，2017;侯丽娟，2014;占艳萍，2015;陈万勤，2017;王治，2015）。以上都是通过拉近了学生与数感的心理距离，将抽象的数学知识转化为具体形象的生活化问题。而所有的这些努力，最终想要的目的是对学生理解、掌握和运用抽象的数学知识进行引导。解释水平是指人们对于事物表征的不同抽象水平（黄俊等，2015），是一种社会认知理论。部分学者认为，解释水平也可以是一种人格变量（黄俊等，2015;黄俊等，2016），反应一个人的认知加工是倾向于抽象还是具体。在解决数学问题时，往往需要学生抽象出问题最本质的关系，在生活中对事物具有不同抽象表征的学生，其解释水平是否有助于他们发展出更好的数感，解决数学问题呢？因此，本研究试图探索解释水平对小学生的数感的影响。

1.1 数感

“数感”来源于英文文献中的“Number Sense”。在“美国数学课程标准”表述中，“Number Sense”是伴随着学生对数、数的表示方式、数与数之间的关系、数系统的理解以及数运算、运算律等的理解和运用而逐步发展的。“Number Sense”不仅限于感知的范围，而且含有思想的成分。

虽然许多学者和数学教育工作者就数感的重要性达成共识，但目前仍无一个定义可以被广为接受。Gersten等指出：没有任何两个研究者以完全相同的方式定义数感。而认知科学家和数学教育工作者以不同的方式定义数感，使得问题变得更加复杂。虽然数感的定义难以明确界定，但我们可以从下列学者对数感的诠释发现一些特点（乔福强，2010;王本法，乔福强，2012）。

Sowder认为，数感是一个使人连接数字与运算的组织良好的概念网，可用于辨别数字相对和绝对大小、对数字作质和量的判断、识别计算不合理的结果、以及用非算则形式进行心算。

Howden认为，数感是一种对数字的特殊感觉，是人们对数与数或数与现实世界的直觉。

Trafton认为，数感比较像是把数当做量来处理，而不是把数当做抽象的、正式的东西来觉察。

Hope认为，数感可以是一种对数字及其多样化使用与解释的“感觉”，计算时对正确程度的“了解”及使用数字支持和论证“常识”也可以是产生合理估计、侦测算数错误、选择有效的计算程序及辨识数字组型的“能力”。

Carpenter认为，数感最重要的是弹性的操作数字。

综上，研究者们对数感定义有三个主要方向：数感是一种直觉，这种直觉在对数的解释时会出现;数感是一种连接，能够迅速组织数与数、数与情景，构成一个概念网;数感是一种策略，能灵活弹性的处理各种关于数的问题。因此，本研究认为数感是对数（量）和运算在其产生的现实情境中灵活甚至创造性应用的心理倾向。

1.2 解释水平理论

解释水平理论是一种“认知理论”。解释水平是指人们对于事物表征的不同抽象水平。从1998年Liberman与Trope发表了关于时间解释的理论至今，总体来讲解释水平理论研究向深度和广度两个方向发展。深度即解释水平理论底层心理机制的研究，即探讨心理距离的四个维度（时间距离、空间距离、社会距离、可能性或者概率）对于解释水平变化的影响;广度即探讨解释水平理论在选举、说服、谈判、消费者行为等领域的应用。根据对事物的抽象程度的高低，解释水平分为高解释水平和低解释水平。高解释水平是抽象的、簡单的、结构化及连贯的、去背景化的、首要的及核心的、本质的、上位的、与目标相关的，例如把钱表征为文字;而低解释水平是具体的、复杂的、无组织及不连贯的、背景化的、次要的及表面的、下位的、与目标无关的，例如把钱表征为图片（孙晓玲等，2007;黄俊等，2015）。目前对于解释水平的研究除了综述性文章外，其他的研究大致有以下几个特点：

1、研究者主要将解释水平当成是自变量，研究解释水平对因变量的影响。或者将解释水平当成是一个自变量和一个因变量之间的调节变量或中介变量。当解释水平为中介变量时，根据中介变量定义，自变量X会影响中介变量M，进而影响因变量Y。我们可得到将解释水平当成因变量的研究方法：只看X→M的回归分析，解释水平就变成了因变量。

2、从解释水平的的视角来解释某个现象，如米雪（2012）《解释水平理论在学习中的应用》。

3、解释水平与另一个变量的关系研究。

综上，本研究利用Vallacher与Wegner的BIF问卷对个人的解释水平进行测量，进而探索解释水平与小学生数感的关系。

2 研究方法

2.1 研究对象

在涪陵城区十三小学四到六年级学生发放问卷260份，获得有效问卷254份，有效回收率为97.7%。其中，男性116人（44.6%），女性138人（55.4%）;四年级90人（35.4%），五年级84人（33.1%），六年级80人（31.5%）。

2.2 研究工具

解释水平问卷采用Vallacher与Wegner于1989年编制的BIF问卷，即行为鉴别项目测试（Behavior Identification Form，BIF）。量表共25题，每题描述了两种行为：高解释水平行为和低解释水平行为。其中，反向计分题为1、3、4、5、7、8、10、13、14、16、20、23、24。量表最终得分为所有题目得分之和，得分越高表示解释水平越高。该问卷内部一致性系数ɑ为0.85，重测效度为0.92。

小学生数感问卷采用自编的小学生数感问卷，问卷共11题，包含4-6年级学生对相应的数与运算的一般理解。量表最终得分为所有题目得分之和。测量结果与数学成绩排名显著相关r = 0.174，p <0.01，这表明小学生数感问卷有效反应了学生数感水平。

2.3 实施程序

由于小学四、五、六年级学生，理解力还没有完全成熟，因此答题时，调查人员可为学生现场口头解释不理解的问题，但对答案的选择不做倾向性引导。主试说完指导语后发放问卷，学生回答完毕后当场收回问卷。随后，分别收集每班的数学教师根据印象评价的每位同学数学在班级中的排名情况。

2.4 统计处理

采用Excel对数据进行整理，用SPSS 22.0 进行统计分析。采用的统计方法包括独立样本t检验，相关分析和回归分析，检验水准 ɑ = 0.05。

3 研究结果

3.1 解释水平、数感在性别上的差异

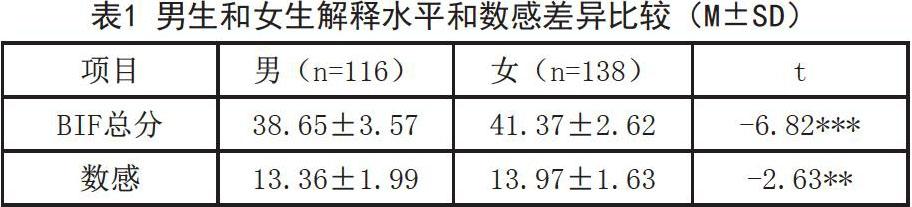
表1结果显示，男生和女生在解释水平和数感上的差异均极其显著。女生的解释水平显著高于男生，女生的数感也显著高于男生。

3.2 解释水平、数感的相关与回归分析

相关分析发现，性别（r（254）=0.167，p<0.001）、解释水平（r（254）=0.542，p<0.001）与数感显著相关。因此，进一步进行回归分析。

以解释水平为自变量，数感为因变量，进行分层回归分析。表2结果表明：解释水平对数感具有显著的正预测作用（β解释水平 = 0.567，p < 0.001），且能解释总变异的26.9%。人口统计学变量性别解释了总变异的2.4%。

4 讨论

4.1 解释水平、数感在性别上的差异讨论

基于对解释水平对小学生数感的影响研究得出：小学生的解释水平存在明显差异，女生的解释水平比男生要高。这与小学阶段女生普遍比男生发育成熟快的规律一致（林崇德，2018）。这说明我们在进行数学教学时，要关注小学阶段男女发展的差异。

4.2 解释水平、数感的相关与回归分析讨论

本研究发现，解释水平这种对事物的表征的抽象水平和数感非常相关。解释水平显著影响数感，解释水平能够解释小学生数感26.9%的变化。解释水平越高的学生就越能够抽象出问题最本质的关系，对于理解掌握数学知识，提高数学成绩，提高学习数学的信心，以及运用数学知识解决生活中的实际问题大有好处。这提醒我们在教学过程中，要结合学生的认知情况分类教学。此外，根据解释水平理论的观点，培养意识上，需要教师有培养具有不同解释水平的学生抽象表征水平能力的意识，对事物有具体表征水平的学生，引导和训练其抽象表征的倾向，并反复训练，渐渐培养其抽象表征能力;具体教学方法上，需要教师通过数学知识与生活具体情境的联系，将抽象枯燥乏味的知识形象化表达给学生，让学生深刻理解和运用数学知识;教授知识时，要求教师尽可能传达知识的本质，让学生理解知识的核心关系，从而提高学生的迁移和应用能力。此外，根据人的成长规律，孩子从小发展更多的是对事物具体表征的能力，教师要有长远眼光、关注核心，关注本质，引导学生形成对事物抽象表征的能力，最后让学生达到在高低解释水平（抽象具體表征）间自由转换的能力，虽然人格变量改变起来相对缓慢，但这种能力培养出来对学生的发展非常有益。

5 结论与展望

综上所述，本研究结论如下：在性别上，解释水平和数感存在显著差异，小学女生解释水平和数感均显著高于男生。解释水平和小学生数感显著相关，解释水平对小学生数感的解释率为26.9%，即小学生数感的变化的26.9%可由解释水平来解释。

本研究首次将解释水平理论与小学生数感结合进行研究。未来的研究，在研究对象选取上，可以更加进行全面扩展;研究方式上，本研究采用的是问卷调查的方式，未来结合实验和追踪研究更能说明解释水平对学生数感发展的影响。此外，言传身教的重要性是有共识的。父母和教师的解释水平倾向对学生潜移默化的影响大也有研究之处。

参考文献

[1]刘兼，孙晓天.数学课程标准解谈[M].北京：北京师范大学出版社，2005.

[2]潘星宇，俞清怡，苏彦捷.从数感看儿童数表征的发展[J].华 东 师 范 大 学 学 报（教 育 科学 版）.2009（4）：30-41.

[3]夏云川，曹晓君.儿童早期数感发展的影响因素及教育建议[J].教育导刊（下半月），2017（8）：36-39.

[4]侯丽娟.浅谈小学生数感的培养[J].吉林教育，2014（11）：84-84.

[5]占艳萍.浅谈小学生数感的培养[J].教育界：综合教育研究，2015（1）：137-137.

[6]陈万勤.小学生数感的培养[J].学周刊，2017，4（4）：65-66.

[7]王治.浅谈小学生数感的培养[J].才智，2015（7）.

[8]黄俊，李晔，张宏伟.解释水平理论的应用及发展[J].心理科学进展，2015，23（1）：110-119.

[9]黄俊，李晔，张宏伟.解释水平理论完善过程中的四个问题[J].心理科学，2016，（4）：887-892.

[10]乔福强.数感、数学效能感与数学成绩的关系[D].济南大学，2010.

[11]王本法，乔福强.数感、数学效能感与数学成绩的关系研究[J].国特殊教育，2012（6）：87-91.

[12]孙晓玲，张云，吴明证.解释水平理论的研究现状与展望[J].应用心理学.2007，13（2）：181-186.

[13]米雪.解释水平理论在学习中的应用[J].考试周刊，2012，（51）：165-167.

[14]林崇德.发展心理学（第三版）[M].人民教育出版社，2018.