Thickness Effect of Nanocrystalline Layer on the Deformation Mechanism of Amorphous/Crystalline Multilayered Structure

Wen-Jay Lee ,Yu-Chien Lo,Anchen Yang,Kuanpeng Chen and Nan-Yow Chen

1 National Center for High-Performance Computing,No.22,Keyuan Rd.,Central Taiwan Science Park,Taichung City 40763,Taiwan.

2 Department of Materials Science and Engineering,National Chiao Tung University,No.1001 University Rd.,Hsinchu 30010,Taiwan.

3 National Center for High-Performance Computing,No.7,R&D 6th Rd.,Hsinchu Science Park,Hsinchu City 30076,Taiwan.

Abstract:Different thickness of amorphous/nanocrystalline multi-layered structure can be used to modulate the strength and ductility of the composite materials.In this work,molecular dynamics simulations were conducted to study the thickness effect of nanocrystalline layer on mechanical properties and deformation behavior of the Cu64Zr36/Cu multi-layer structure.The stress-strain relationship,local stress,local strain,and deformation mechanism are investigated.The results reveal that the change of thickness of the crystalline layer significantly affects the mechanical properties and deformation behavior.As the strain at the elastic region,the amorphous Cu64Zr36 layer dominates the mechanical behavior,leading the fact that Young’s modulus,first yielding stress,and first yielding strain are close to that of Cu64Zr36 BMG.As the strain at the plastic region,the contribution of the crystalline layer on the mechanical behavior becomes more and more significant with increasing the thickness of the crystalline layer.For the thickness ratio (amorphous/crystalline) of 4,the shear band deformation of amorphous layer dominates the mechanical properties.For the thickness ratio is 1,the glide dislocation of the crystalline layer dominates the stress-strain behavior.

Keywords:Molecular dynamics,Cu64Zr36 bulk metallic glass,Cu64Zr36/Cu,layered structure,shear band,mechanical property,deformation.

1 Introduction

To improve and understand the mechanical properties,there have been more research carried out form the beginning of the metallic glass.Due to promising behavior of metallic glass that it has been showing high strength,high hardness and likewise extensive investigations were applied for industrial use [Nishiyama,Amiya and Inoue (2007)].Metallic glass dominant mechanical properties are suitable for applications [Nishiyama,Amiya and Inoue (2007)],but there is still need of more development for better applications due to their mechanical deformation behavior [Jiang and Atzmon (2006)].Mechanical deformation behavior of metallic glass is not clearly understandable.Therefore,several studies have been proposed to understand the mechanically deformation of metallic glass.Shear band is the main cause of mechanical deformation in metallic [Feng,Wang,Pan et al.(2015);Zhang,Li and Li (2017);Cui,Abad,Wang et al.(2016)].

Plastic deformation is produced by shear band propagation and initiation in ductile manner metallic glass [Feng,Wang,Pan et al.(2015);Zhang,Li and Li (2017);Cui,Abad,Wang et al.(2016)].Shear bands caused inhomogeneous deformation behavior in amorphous alloys.Quantitatively understanding of shear bands mechanism has been stated [Gao (2006);Shen and Zhemg (2010);Shi and Falk (2008);Sun,Pauly,Tan et al.(2012)].Criteria to define the shear bands initiation and propagation is reported by Zhang et al.[Zhang,Li and Li (2017)].Molecular dynamics simulation increases the understandability of atomic structure explaining shear bands in metallic glass as compared to the other studies have been carried out for shear bands formability [Greer,Cheng and Ma (2013)].The interaction phases of shear bands propagation strongly depend on the mechanical properties.Greater young’s modulus and smaller Poisson ratio will greatly contribute in interaction of shear band phases [Yang,Sun,Chen et al.(2017)].Deformation physicality of metallic glass comparably explained by strain localization,which could occur at low temperature and slow strain rates and it could be affected by the external size of the sample.Many strategies are discussed to increase/improve the mechanical properties of bulk metallic glass [Inoue,Wada and Louzguine-Luzgin (2007);Kumar,Ohkubo and Hono (2009);Lee,Huh and Fleury (2006)].

Amorphous alloys plasticity can be increased by changing the size of specimens and for better understanding of fundamental mechanical deformation structure [Guo,Yan,Wang et al.(2007)].Size of the particles can significantly effect the shear band propagation as small size particles will show strong restrained as compared to particles with big size [Park,Kim,Stoica et al.(2011)].By changing the layer thickness ductility can be increased and introducing nano-crystalline phase which would restrained the shear band [Wang,Yang,Jiang et al.(2014);Hufnagel,Fan,Ott et al.(2002)].Multilayers approaches have been defined to understand the exact phenomena which can excites the main cause of plastic deformation [Cui,Abad,Wang et al.(2016)].

ZrCu bulk metallic glass (BMG) been extensively studied.Because a specific composition ratio of Cu64Zr36presents a glass forming ability (GFA),it is easier to obtain a larger size specimen from experiment and has relatively high yield strength,modulus,hardness,along with the lowest plasticity,compared to the CuxZr100-x with different compositional ratio.The results originate from the densely packed nature associated with the enrichment of the pentagonal clusters or icosahedron [Park,Jang,Wakeda et al.(2007)].The main deformation mechanism of BMG,named shear band,is a narrow zone of intense shearing strain.However,the passed work has found that the formation of shear band is strongly related to the thickness of the examined sample.As the thickness of the amorphous layer ＞100 nm,shear band is allowed to produce when a loading impose on the specimen.While the thickness of the amorphous layer ＜100 nm,the formation of shear band is restrained.The amorphous region could allow a greater strain.Cu64Zr36(amorphous layer)/Cu(crystalline layer) multi-layered structure possesses a higher strength and strain than the pure Cu crystalline.In addition,one can vary the material properties by changing the thickness of either the crystalline or amorphous layers.In order to obtain a clear understandable view of plasticity of metallic glass multilayered structure.Molecular dynamic simulation was employed to study the mechanical deformation and properties of Cu64Zr36(amorphous)/Cu(crystal) multi-layered structure in this work.Thicknesses effect of crystalline layer on the mechanical and deformation mechanism are discussed.

2 Methodology

2.1 molecular dynamics

Large-scale Atomic Molecular Massively Parallel Simulator (LAMMPS) [Plimpton (1995)] as a molecular dynamics simulator was employed to study the mechanical properties of the Cu64Zr36metallic compound.All atomic interactions are modelled by the many-body,embedding atom method (EAM) potential [Cleri and Rosato (1993)].In this work,MD simulations were performed in both isothermal-isobaric ensemble (NPT) and canonical ensemble (NVT) systems for different purposes of simulations.Isothermalisobaric ensemble is a statistical mechanical ensemble that maintains constant temperature and constant pressure applied,whereas the canonical ensemble represents the mechanical system in thermal equilibrium with a heat bath at a desired temperature.Nosé-Hoover thermostat [Nosé (1984);Hoover (1985)] andParinello-Rahmanbarostat [Parrinell and Rahman (1981)] and Parinello-Rahman barostat [Parrinell and Rahman (1981)] were used to maintain the target temperature and pressure.The velocities of the atoms were randomly assigned according to a Maxwell distribution.The time integration of the Newtonian equations of motion was performed by using Velocity Verlet algorithm [Swope,Andersen,Berens et al.(1982)] to obtain the new velocities and positions of each atom.The integration time step was set 1 fs.All MD simulations were recorded every 1 ps for recoding the trajectory frame and analyzing properties.A pre-equilibrium process of 2 ns was performed at 500 K temperature and 1 atm pressure before the quench process for the relaxation of initial structure.

2.2 Model of Cu64Zr36 bulk metal glass

In this work,the mechanical and deformation behavior of Cu64Zr36/Cu multi-layered structures with different thickness of Cu crystalline are discussed for understanding the layered structure effect on the shear band formation and translation.The results will compare with those of Cu64Zr36BMG.As a result,four slab samples are created,which include the three multi-layered model and a Cu64Zr36BMG model.For the Cu64Zr36BMG,the slab sample with dimensions of 55 nm(X)×27 nm(Y)×5 nm(Z) contained 230,400 atoms,which was produced by quenching it from the melt.Periodic boundary conditions (PBCs) were initially applied in three directions.The system was fully equilibrated at 2000 K and zero external pressure for 2 ns in a NPT ensemble using a Nose-Hoover thermostat to ensure chemical homogeneity.Then the samples were cooled to 50 K at a rate of 1010 K·s-1in order to form MGs.Fig.1 shows the system volume as a function of temperature.It is observed a transition point that greatly changes the slop at 720 K,which is the Glass transition temperature (Tg) that defines the temperature at which the amorphous system transforms from glassy state (low temperature domain) to a rubbery state (high temperature domain).The result of 720 K is corresponded to that observed by experiment of 745 K.

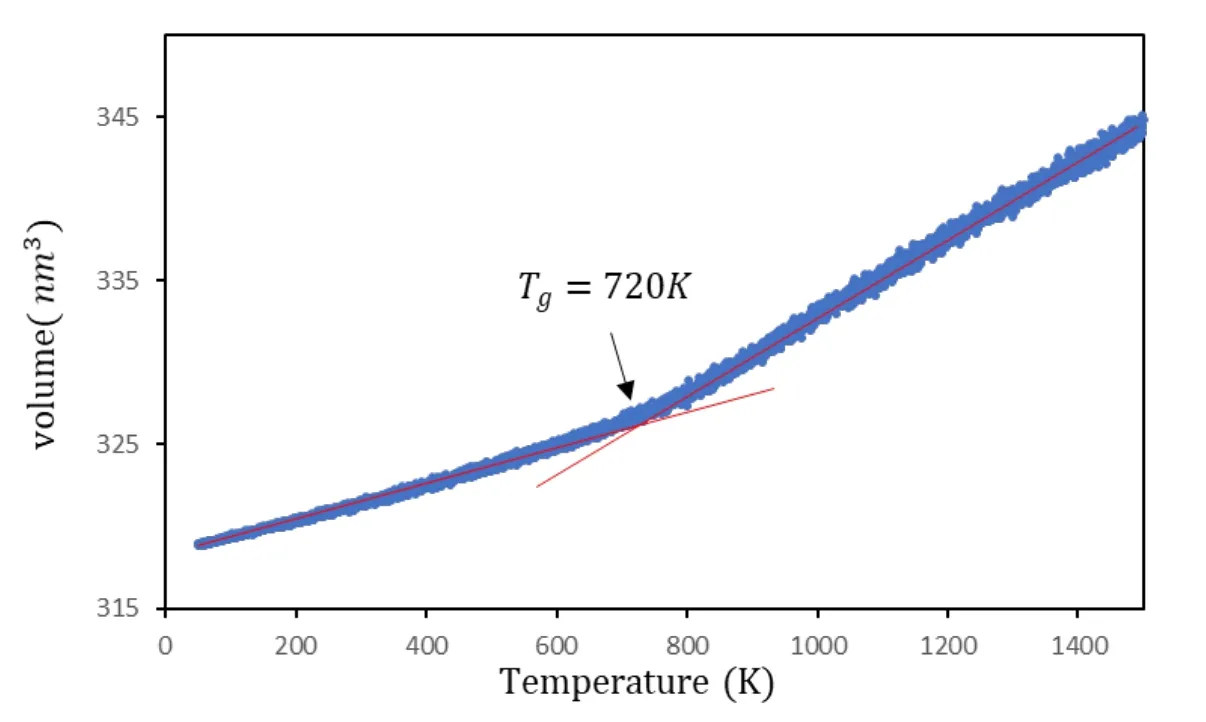
Figure 1:System volume as a function of temperature for Cu64Zr36 model

2.3 Model of Amorphous Cu64Zr36/ crystalline Cu multi-layered structure

In order to discuss the thickness ratio effect on the mechanical properties for amorphous/ crystalline(A/C) multi-layered structure,three thickness ratios of A/C with fixed thickness of amorphous layer are considered.The amorphous layer is considered to be the same as the equilibrium structure of Cu64Zr36BMG mentioned in Section 2.2,while the crystal layers of 55 nm,27 nm,and 13.5 nm in thickness were considered.The crystal structures were first equilibrium and then stack on the amorphous layer with a gap of 0.2 nm.The combination would roughly result in the thickness ratio of A/C=1(55 nm:55 nm),2(55 nm:27 nm),and 4(55 nm:13.5 nm).PBCs were applied in all three directions.To generate the relaxation interface of Cu64Zr36/Cu,the system was firstly fully equilibrated at 750 K (＞Tg) and zero external pressure for 400 ps in NVT ensemble.Then,the system was cooled to 300 K.The systems were equilibrium in NVT for 100 ps,and then switched to NPT for relaxing the volume constrained.The corresponding process is shown in Fig.2.Here,it points out that the equilibrium structure (after 100 ps NPT equilibrium at 300K) obtained from the initial annealing temperature of 1000 K is also examined.Fig.3 demonstrated that the interfacial structure in the case of 1000 K is correspond to that of 750 K.Finally,the samples were cooled to 50 K and equilibrium for 100 ps again to ensure the structure relaxation at the interface.

Figure 2： Annealing process for binding the amorphous Cu64Zr36 and crystalline Cu

Figure 3： Radius distribution function of the interfacial layer of Cu64Zr36/Cu with different cooling conditions

Figure 4： Illustration of simulation model for multilayered Cu64Zr36/Cu with thickness ratio A/C=2

Afterward,PBCs were only imposed in the Y and Z directions.Fig.4 illustrates the equilibrium model of the Cu64Zr36/Cu multilayer structure with the thickness ratio A/C=2 for Cu64Zr36and Cu.Due to the PBCs in the system,the model can be considered as a multilayer structure.All samples were deformed by applying a constant strain rate of 108s-1(quasi-static compression) in X direction at a constant temperature of 50 K.The Y and Z directions were kept at zero external pressure during compression.

3 Result and discussion

Fig.5 shows the stress-strain relationship of Cu64Zr36/Cu and Cu64Zr36BMG under uniaxial compression.For the BMG system,it is observed that the stress increased linearly with strain until ＜3% in the initial elastic deformation stage;after which,the curve deviated from the initial linearity.Young’s modulus E is the slope of the linear portion of the stress-strain curve.The calculated value is around 70.44 GPa.The yielding stress σyis 3.35 GPa at the yielding strain εyof 6.4%,which is the stress required to initiate apparent plastic flow.Structure disordering became significant when the amorphous solid began to flow,causing the material in the deformed regions to soften and achieve a steady-state flow in the BMG.As the strain is higher than the yielding strain,the alloys exhibited an abrupt decrease in strength,corresponding to spontaneous shear localization into a narrow band [Cao,Cheng and Ma (2009)].It is note that the yielding stress,Young’s modulus,and yielding strain for Cu64Zr36BMG are all corresponding to those observed by theoretical studies [Zhang,Li and Li (2017);Lee,Park,Kim et al.(2007)].In addition,the yielding strain and yielding stress are both much higher than those of poly grain Cu (εy＜5%) [Xiang,Cui and Tian (2013)].As the strain is higher than the yielding strain,the stress decreases until ε=10.5%.The decrease of the stress can be attributed to the accumulation of shear localization,which finally leads to the formation of the shear band in the BMG system.In the following,the stress remains at 2.2 GPa with increasing strain,which can be regarded as the flow strength of the glass or the strength of a propagating shear band.In the experiment,the rapid drop usually leads to fractures,or end of plastic deformation.Due to the high strain rate limitation of MD simulation,fracture cannot be fully captured.Instead,the drop of the maximum stress in the stress-strain curve can be a useful indicator for plasticity.

Figure 5:Stress-strain relationship for the Cu64Zr36 and Cu64Zr36/Cu multi-layer structures with different thickness ratios

The stress-strain behaviors for Cu64Zr36/Cu multilayer systems are different than that of Cu64Zr36BMG,which reflects the different deformation mechanism.Note that the multilayer system with different ratio cases possesses two yielding stress (σy,1and σy,2),where first yielding takes place at the same yielding strain (ɛy,1) of BMG system.Tab.I summarized the mechanical properties for both the multilayer and BMG systems.It is found that the Young’s modulus for multilayer system are slightly lower than that of the of BMG system,and the value slightly decreases with increasing the thickness of crystalline layer.After the first yielding strain,the stress-strain curves for multilayer structures do not decent directly,but first go through a short plastic strain (6.35 %＜ε＜8.90%) attributed by the crystalline layer prior to shear banding of Cu64Zr36layer and suddenly drop after the second yielding strain(ɛy,2).With increasing the fraction of Cu thickness,the slop gradually changes from negative to positive at the short plastic region,indicating the deformation behavior depends on the thickness of crystalline layer.

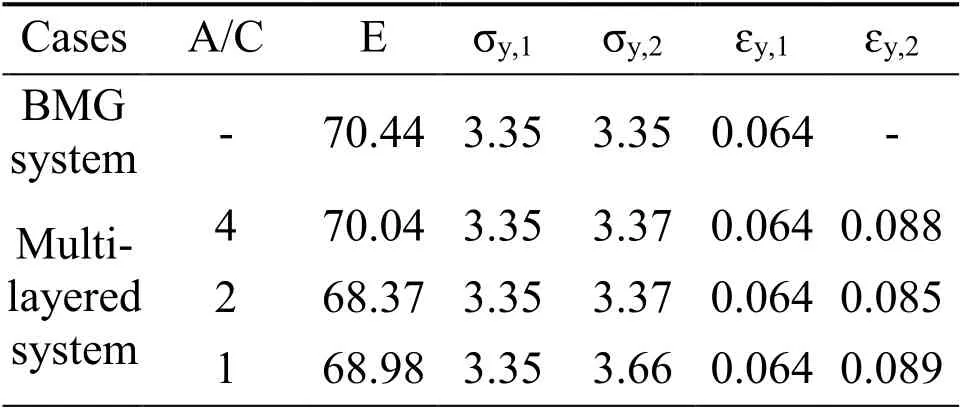
Table 1:Mechanical properties of Cu64Zr36 and Cu64Zr36/Cu multi-layer structures.E,σy,1,σy,2,ɛy,1,and ɛy,2 indicate the Young’s modulus (GPa),first yielding stress (GPa),second yielding stress (GPa),first yielding strain,second yielding strain,respectively

Figs.6-7 show the atomic strain distribution of the multilayer structures with thickness ratio A/C=4 and 1,respectively.As the strain lower than the first yielding strain,the imposed strain is accommodated inhomogeneously in the local region of amorphous layer and homogeneously in crystalline layer as shown in Figs.6(a) and 7(a).As the strain higher than the second yielding strain,the shear band propagation in the amorphous layer induces the slip deformation in the crystalline layer,resulting a sudden descent of stress.Figs.8(a)-8(d) illustrate the corresponding deformation process for the case with thickness ratio A/C=4,where the arrows indicate the slip direction that initiated by the propagation of shear band.When crossing the Cu layer to the Cu64Zr36/Cu interfaces,the dislocations will drag Cu atoms into the opposite Cu64Zr36layer leading to chemical mixing and even local amorphization of the crystalline layer (Figs.6(d)-6(f)) at the interface.As the strain is higher than the 2ndyielding strain,the stress exhibit an obvious zig-zag fluctuation.A thicker the thickness of Cu layer is,a stronger the fluctuation will be,which reveals that the mechanical behavior is gradually dominated by the crystalline layer with increasing the thicker cases,as can be seen in Figs.6(h) and 7(h).The crossslip deformations become more and more significant with increasing the thickness of crystal,which leads the work hardening and dominate the mechanical behavior of the multi-layered system.However,both the amorphous and crystalline layer play important role in the deformation for thickness ratio A/C=4.The amorphous solid becomes easy to flow,which causes the material in the deformed regions to soften and achieve a steadystate flow rather than work-hardening with strain increasing.As a result,the stress for the thicker case has a higher rising amplitude than that for thinner one.It is summarized that a multilayer structure of amorphous phase and crystalline phase might suppress shear bands and have certain plastic co-deformation.

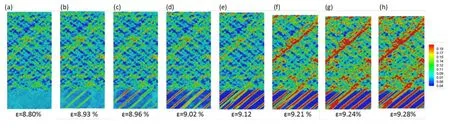
Figure 6:Distribution of von Mises shear strain for the Cu64Zr36/Cu multi-layer with thickness ratio A/C=4

Figure 7:Distribution of von Mises shear strain for the Cu64Zr36/Cu multi-layer with thickness ration A/C=1

Figure 8:Illustrations of the glide dislocation initiated by the amorphous layer.Note that the atomic strain＜0.14 are eliminated in order to clearly display the deformation process

Figs.9-10 show the local stress distribution for the Cu64Zr36/Cu multi-layer structure with thickness ratio A/C=4 and 1 before and after the second yielding strain.It is observed that the amorphous layer possesses higher stress than the crystalline layer in Figs.9(a) and 10(a),indicating the fact that the amorphous layer plays the main role to dominate the stress-strain behavior.As a result,the fact also explains why the Young’s modulus of the Cu64Zr36/Cu multi-layer structure for different thickness are close to that of the Cu64Zr36BMG system.For the case of thickness ratio A/C=4,the amorphous possess a high compression stress and the crystalline layer possess a low tensile stress as the strain approaches the second yielding strain.The tensile stress is due to the thin thickness of crystalline layer that limits the degree of freedom of atomic motion in the normal direction and causes a strong lateral tension.In addition,the inhomogeneous strain localization of amorphous layer that occupies the most fraction of the system disperses the imposed normal strain in Fig.6(a).and results in work soften.Therefore,the case with thickness of 13.5 nm of Cu layer (thickness ratio A/C=4) cannot easily prevent the cross-phase propagation of shear strain.For the case of thickness ratio A/C=1 (55 nm in thickness for Cu layer),it is found that the stress homogeneously distributes on the crystalline layer as can be seen in Fig.10(a).Compared to the work soften of thinner case,a thicker thickness of crystalline layer provides a higher degree of freedom to accumulate the compression stress in Cu layer with elastic deformation.Consequently,both amorphous and crystalline layers play the roles to bear the compression strain,resulting in the increase of stress-strain curve after the first yielding.

As the strain passed the yielding strain,the stress significantly drop,as was observed in stress-strain diagram of Fig.5 and the corresponding stress distributions of Figs.9(a)-9(h) and 10(a)-10(g).The compression stress in the amorphous layer significantly decreases and switches to the tensile stress in amorphous layer.With decreasing the thickness ratio A/C (increasing the thickness of crystalline layer),the region with tensile stress increase.Consequently,the value of the drop stress for the case with ratio thickness ratio A/C=1 is much lower than that with thickness ratio A/C=4 as shown in Fig.5.The compression stresses are mainly concentrated in the strain localization regions indicated by red circle in both Figs.8 and 9,and the tensile stress is localized around them.

Figure 9:Von Mises stress distribution for the Cu64Zr36/Cu multi-layer with thickness ratio A/C=4.The range of strain localization is marked in circles in red

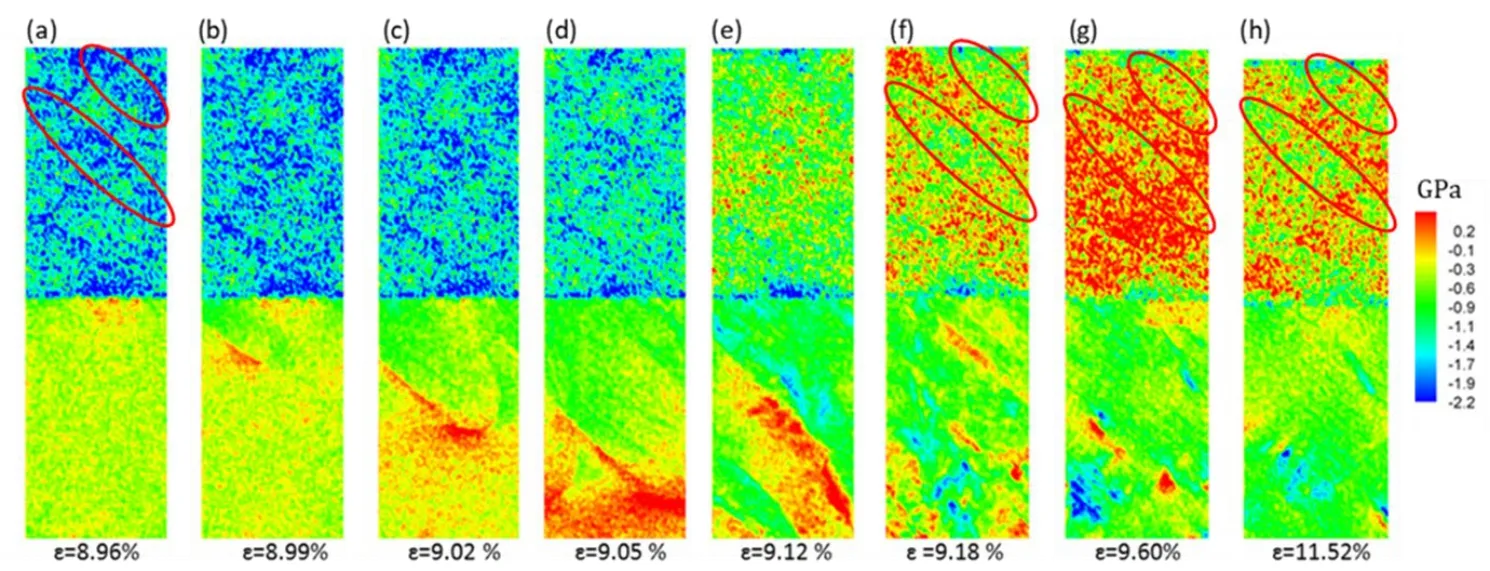
Figure 10:Von Mises stress distribution for the Cu64Zr36/Cu multi-layer with thickness ratio A/C=1.The range of strain localization is marked in circles in red

4 Conclusion

In this work,molecular dynamics simulations have been conducted to investigate the thickness of crystalline layer effect on mechanical properties and deformation behavior of the Cu64Zr36/Cu multi-layer structure.In the elastic deformation state,the stress is accumulated in the amorphous layer as the external strain is imposed.The stress-strain behavior is dominated by the amorphous layer.Young’s modulus decreases with increasing the A/C ratio for the Cu64Zr36/Cu multi-layer structure.In the plastic state,the stress of the multi-layer system would go through two yields before the first drop.The first yielding is due to the strain localization on the amorphous layer,while the second yielding (drop of stress) is attributed to the glide dislocation from the crystalline layer.As the stress passes the first yielding strain to second yielding strain,the strain localization would lead the work soften for a thinner thickness of crystalline layer.However,the case with a thinker the thickness of crystalline layer leads the increase of stress.After the drop of stress,the thicker crystalline layer might suppress the formation of shear band.The glide dislocation of crystalline layer will dominate the stress-strain and deformation behavior of Cu64Zr36/Cu multi-layer structure.

Acknowledgement:The authors would like to thank the Ministry of Science and Technology of Taiwan for financially supporting this research under Contract Nos.MOST 107-2218-E-007-012- and 107-2221-E-492-011-MY3.Support of significant computing resources from the NCHC in is also acknowledged.