NdMnO3亚微米团簇磁热效应的研究

陈建宝,洪 波

(中国计量大学 材料科学与工程学院, 浙江 杭州 310018)

近些年来,钙钛矿型锰氧化物REMnO3(RE一般为3价稀土元素)由于其独特的电性能和磁性能引起了人们大量的关注和研究[1],又由于钙钛矿结构组成的灵活性,大家对其的研究又任重而道远。其中在磁性能方面,钙钛矿型锰氧化物在发生铁磁到顺磁的相变时存在着显著的巨磁阻效应(CMR)[2]和磁热效应(MCE)[3]。接着又有人通过姜-泰勒效应和双交换理论模型来解释钙钛矿型锰氧化物的这些性质[4-5]。而磁致冷技术正是运用了磁热效应而诞生的一种具备环保、节能、静音优势的新技术,从而具有广阔的应用前景。对于磁热效应,除了高磁熵变外,相对制冷能力(RCP)更适合用来反映一种磁致冷材料的能力[6],其定义为

RCP(S)=|ΔSM|max×δTFWHM。

(1)

式(1)中,(ΔSM)max为最大磁熵变,δTFWHM为最大磁熵的半高温宽。

随后由于纳米材料的兴起,钙钛矿型锰氧化物的纳米材料也受到了广泛的关注。与一般的块体材料相比而言,纳米材料随着其粒子尺寸的减小,表面和界面作用的增强,从而对其性能引起了不小的变化[7]。对磁热效应而言,由于纳米材料表面一系列缺陷的增多,使其不饱和磁矩增多,进而使其饱和磁化强度减小,从而又使磁熵变减小。但是，又由于相变温度宽化,使其高熵变温区宽化,相较RCP还是未知数。纳米结构的磁致冷材料成为了一个研究热点[8-11]，但对于亚微米级的材料来说,结构在块体与纳米材料之间,如果性能既有块体材料的高熵变,又有纳米材料的宽熵变温区的话,这将会是一个不错的选择。

综上所述,本实验打算选择用溶胶凝胶(sol-gel)法来制备亚微米团簇NdMnO3,并且探究其磁热效应,为磁致冷材料的选择更进一步。

1 实验过程

1.1 制备过程

本文运用了溶胶凝胶(sol-gel)的方法[12]来制备NdMnO3钙钛矿粉末样品。首先,按2.5 mmol的Nd(NO3)3·6H2O,5 mmol的50 wt% Mn(NO3)2溶液和5 mmol的柠檬酸的比例一起均匀溶解在40 mL去离子水中。搅拌30 min后,在加入几滴乙二醇后再搅拌3 h。之后,将溶液置于80℃恒温油浴锅持续搅拌直至形成干燥褐色凝胶。然后,将凝胶置于马弗炉以1℃/min的速率升至200 ℃预烧2 h,之后将样品研磨至均匀粉末。最后,将样品粉末置于高温马弗炉以1 ℃/min的速率升至1 000 ℃烧结6 h后得到最终样品。

1.2 表征方法

通过X射线衍射分析仪来分析产物的晶体结构特征(XRD,丹东浩元仪器有限公司,DX-2700,辐射源为Cu靶Kα射线,波长为0.154 nm,管电压为40 kV,管电流为40 mA,步进角度为0.02°),颗粒尺寸和形貌用透射电子显微镜(TEM,JEM-1010, JEOL)来分析。磁性能是由Quantum Design的综合物性测试系统测试完成。

2 结果和讨论

2.1 结构分析

样品的XRD峰图如图1,我们发现该方法制备的样品NdMnO3并不是通常结构为Pbnm或者Pnma空间群的NdMnO3,而是由Dyakonov等人[13]首先报道的P21/c空间群的,即其准确的实际结构为NdMnO3.03,这也和制备方法所参照论文的结论所一致。接着,样品NdMnO3的形貌特征由TEM表征,如图2。我们可以形象地看出样品为100 nm至300 nm的亚微米级团簇,也正好符合我们的预期。

图1 样品NdMnO3的XRD图Figure 1 XRD patterns of NdMnO3 sample

图2 样品NdMnO3的TEM照片Figure 2 TEM image of NdMnO3 sample

2.2 磁性分析

为了研究该样品的磁性性能,我们首先测试了磁化强度和温度的关系曲线图(如图3)。其中,ZFC曲线是在无外加磁场下由常温降到50 K,然后加100 Oe的磁场后开始升温测量,而FC曲线是在100 Oe的磁场下由常温降到50 K,然后开始升温测量,两者都在50～150 K的温区下测量而得。

在FC曲线中,我们观察到磁化强度的剧烈下降,这里可能存在着一个磁相变点,类似与方菲等人[14]研究的LaMnO3纳米线。而在ZFC曲线中,刚开始由于磁矩的混乱而在低温阶段电子热运动很弱导致弱磁场无法改变其磁矩,从而表现出一开始磁化强度随着温度上升而增加。然而温度到一定程度后,该曲线如FC曲线一般,也出现了磁化强度的剧烈下降,所以我们认为该材料在这里有着明显的铁磁-顺磁转变的特性。它的居里温度由ZFC曲线的一阶导数曲线可以粗略的确定为68 K。

为了进一步确定其居里温度,我们下面运用了两种方法。第一种利用居里-外斯定律,其公式为χ=C/(T-TC),式中,χ为磁化率(χ=M/H),C为物质的居里常数,T为绝对温度,TC为居里温度。将其变形为

M-1=(T-TC)/(H·C)。

(2)

所以式(2)中,M-1与T的函数关系应该是斜率为正的一条直线,当M-1为0时,T=TC。如图4,红线为该样品数据的拟合直线,表示出该物质的居里温度为(78.4±2.8)K。但是,图中的拟合程度有所欠缺,这与XU等人文中[15]出现的现象非常相似。其中合理的解释是在该材料中由于小尺寸效应也出现了一定的Griffiths相,从而导致居里-外斯定律得到的居里温度有所偏差。

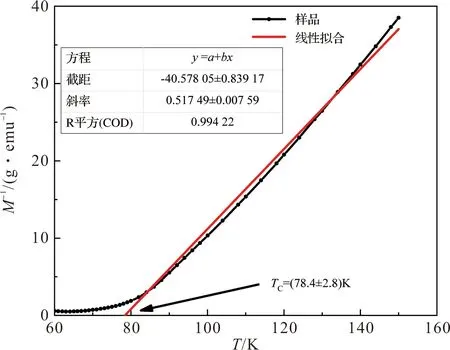
图4 样品NdMnO3的M-1-T的线性拟合图Figure 4 Linear fitting of M-1-T in NdMnO3 sample

第二种方法为绘制出样品NdMnO3的Arrott曲线图,其中选取平均场理论模型((β=0.5,γ=1)较为合适[16],即以H/M为x轴以M2为y轴。我们选取了靠近居里温度的一系列等温磁化曲线(从54 K到76 K以每2 K为间隔),从而绘制出图5。

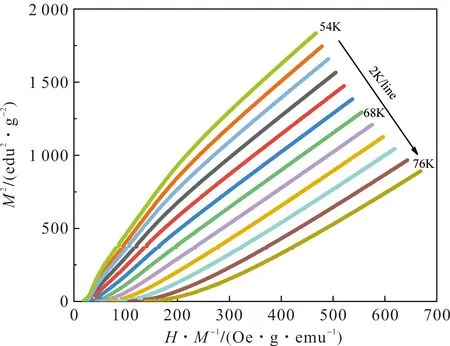
图5 样品NdMnO3的Arrott图Figure 5 Arrott graph of NdMnO3 sample

在图5中,皆为一系列斜率为正的类直线,说明了该相变的本质其实为二级相变。根据该理论模型,在相变温度附近,这些曲线应该为一系列平行直线,且在相变温度时应该为经过原点的直线。从图中可以看出,在68 K附近最为接近该理论模型的论述。然后结合上面两个结果,证实居里-外斯定律并不适用于该材料(存在着较大的误差),而样品NdMnO3的居里温度实际应该在68 K附近。

最后,为了证明其磁热效应同时也可以求证居里温度的所在范围,还需求出该样品在相变温度附近的磁熵变化,一般最大磁熵就在居里温度附近的温区。其中求磁熵的方法由下面给出,在等温过程的磁熵变(ΔSM)由经典热力学[17-18]得出

根据麦克斯韦关系式

最后得到

(3)

式(3)中,H为磁场强度,T为温度,M为磁化强度。而在实验中,我们选择测量一系列连续温度的M-H曲线,在温度和磁场的变化都不大的情况下,可以将ΔSM近似成

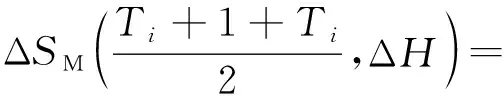
(4)

式(4)中,Mi+1和Mi是在磁场H下Ti+1和Ti温度下的磁化强度。如图6,我们测量了在2T磁场下温度范围为30～118 K的一系列M-H曲线,其中在靠近居里温度的温度间隔为2 K每条线。

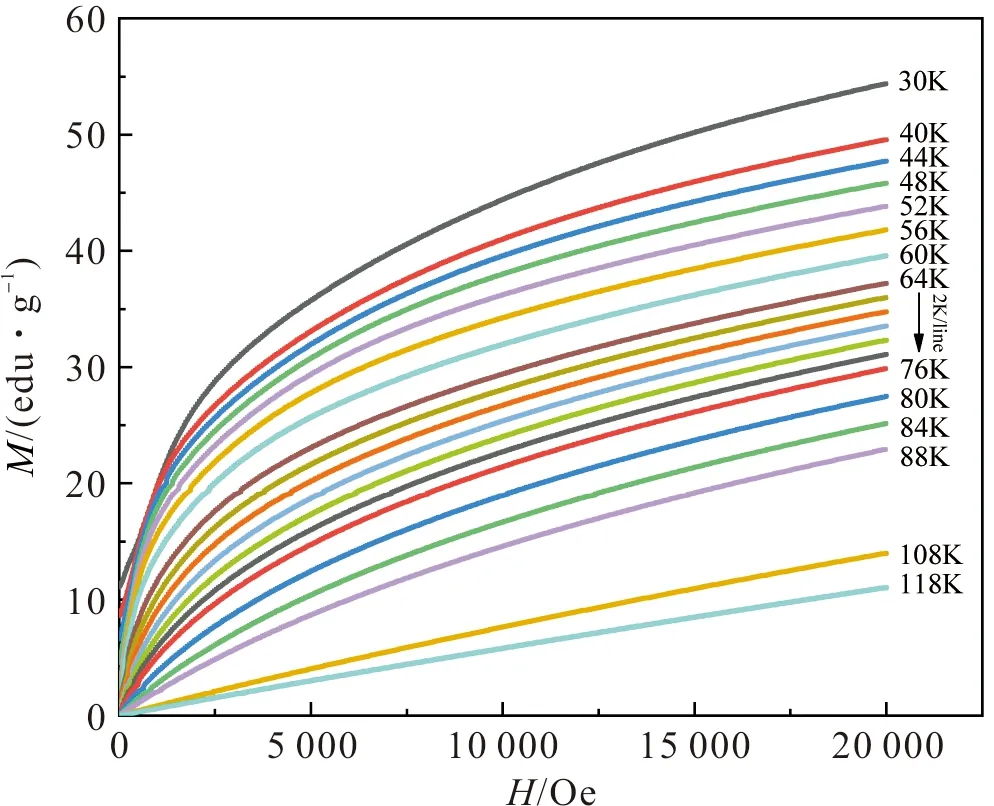
图6 样品NdMnO3的M-H曲线图Figure 6 M-H curves of NdMnO3 sample

根据上述公式和一系列等温M-H曲线,我们可以求出不同温度下的磁熵变化,如图7。从图7中,我们可以得到样品NdMnO3在T=68 K,ΔH=0.5 T、1.0 T、2.0 T时最大磁熵变分别为0.34 J/kg·K、0.69 J/kg·K、1.32 J/kg·K。并且我们还可以确定该样品存在磁热效应,即在相变温度附近有个磁熵增大的峰,且证明该样品的居里温度确实在68 K附近。为了比较不同磁制冷材料的性能,我们还计算了该材料在ΔH=2.0 T的RCP值,为85.8 J/kg。

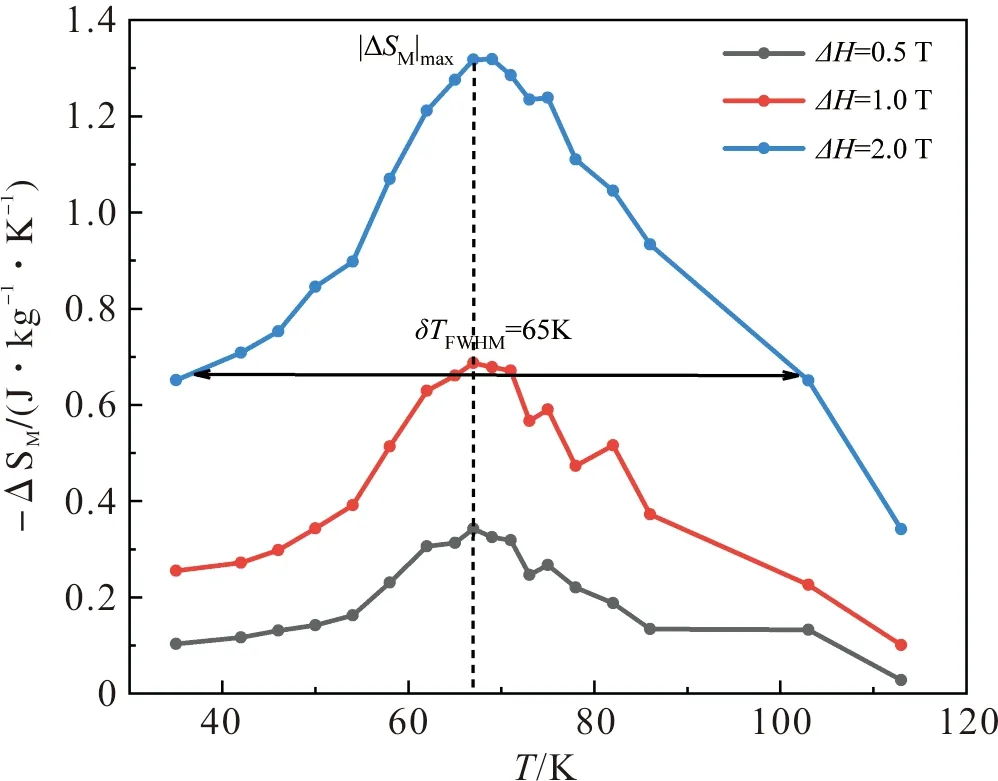
图7 样品NdMnO3的磁熵变化图Figure 7 Magnetic entropy change graph of NdMnO3 sample

3 结 论

本实验运用溶胶凝胶法成功制备了颗粒尺寸为亚微米级的团簇NdMnO3。同时,在ZFC-FC曲线中观察到样品的相变,并且计算出了该样品的居里温度在68 K附近。之后又运用了居里-外斯定律和Arrott图这两种方法去验证该居里温度。最后,我们证明了该样品的磁热效应,并得到它在T=68 K,ΔH=0.5 T、1.0 T、2.0 T时最大磁熵变分别为0.34 J/kg·K、0.69 J/kg·K、1.32 J/kg·K,并且求出它在ΔH=2.0 T的RCP值为 85.8 J/kg,这个值在同类中较为不错。这就表明了亚微米尺度下的此类化合物具有较好的磁热效应,这一发现为后续研发低磁场下高磁制冷的材料奠定了一定的基础。