基于注意力机制的深度协同过滤模型
谢恩宁,何灵敏,王修晖
(中国计量大学 信息工程学院,浙江 杭州 310018)
随着科技的迅猛发展,人们生活中所接触到的信息规模也呈现井喷式增长。为了缓解海量数据检索给人们日常生活带来的不便,推荐系统应运而生。推荐系统一般被定义为:能够通过分析用户行为,对用户兴趣进行建模,从而达到预测用户兴趣并给用户做推荐的目的。推荐系统是帮助用户发现内容,克服信息过载的重要工具。
对于推荐系统领域中传统的推荐算法而言,应用最广泛的是协同过滤算法(Collaborative filtering,CF)[1-2]。目前众多杰出的推荐算法都是基于协同过滤算法,其主要思想是利用用户和项目之间的历史交互信息,对用户和其感兴趣的项目进行建模,从而给出最后的推荐[3-4]。纵观不同类型的协同过滤算法,矩阵分解算法(Matrix factorization,MF)是其中最为流行的推荐算法之一[2,5]。基于矩阵分解的协同过滤算法同样对用户和项目之间产生的历史交互信息进行建模,区别在于该方法分别用一个隐式向量代表用户和项目,而用户和项目之间产生的交互则用隐式向量间的内积来表示。此前大量研究人员致力于使用传统方法增强基于矩阵分解的协同过滤算法,例如,拓展矩阵分解算法到因式分解机[6]、将包含项目内容的主题模型结合到矩阵分解算法[7],以及与最近邻模型相整合[2]。尽管,上述研究提出的方法能够提升推荐系统的推荐效果。但是,基于矩阵分解的协同过滤算法提供的推荐性能还是会受到隐式向量间内积操作的限制[5]。由于隐式向量间内积操作,只是简单地向量间的线性乘法,不足以提取用户和项目之间复杂的历史交互特征。
深度神经网络(Deep neural networks,DNN)作为深度学习技术的基础组件,已经在语音识别、计算机视觉、自然语言处理等领域发挥越来越大的作用[8-10]。DNN对于复杂的抽象特征的提取能力也慢慢展现在我们眼前。将深度学习技术应用于推荐系统中用户和项目之间历史交互信息的特征提取已经迫在眉睫。最近的一些研究中,有将DNN用于推荐系统中辅助信息(项目的文字描述、图片信息等)的特征提取,但没有涉及对基于协同过滤的推荐算法核心问题的改进[7,11]。何等人提出了神经矩阵分解模型(Neural matrix factorization,NeuMF),首次将DNN用于改进基于矩阵分解的协同过滤算法[12]。该模型为集成模型,采用广义矩阵分解模型(Generalized matrix factorization,GMF)提取用户和项目间历史交互数据中的线性交互特征,其中的非线性交互特征由多层感知机模型(Multi-layer perceptron,MLP)来提取,最后结合两部分特征给出推荐。由于NeuMF模型的非线性特征提取部分只是用到了最普通的多层感知机模型,故不能很好的提取用户和项目之间非线性的交互特征。
深度学习技术中的注意力机制,一定程度上模拟了人类视觉中的注意力机制。类比人类视觉中注意力机制能够通过扫描全局图像获取重点关注的目标区域,深度学习中的注意力机制能够帮助普通的多层感知机模型从原始数据中提取出对当前任务更为关键的特征信息。为了更好地利用深度学习技术提取用户和项目之间复杂的非线性交互特征,以便为用户做出更好的推荐,故我们提出了基于注意力机制的深度协同过滤模型(Deep collaborative filtering model based on attention mechanism,DeepCF-A)。我们工作的目标是最终提升推荐系统在隐式反馈数据下的推荐效果。
1 相关理论
1.1 从隐式反馈数据中学习
与显式反馈不同,隐式反馈记录了用户的行为数据(购买历史、点击量、关注量等),并间接反映了用户对项目的偏好。从隐式反馈数据中学习是很有价值的。因为相较于显式反馈数据获取成本高、数据量小的特点,隐式反馈数据往往很容易从内容提供商处获取,并且数据量足够大,能够满足一般深度学习模型训练所需。我们提出的模型要解决的问题是,如何从现有收集到的隐式反馈数据中学习到经验,用于评估用户u对项目i是否感兴趣。我们可以将上述目标抽象成以下公式,即
(1)
接下来用M和N分别表示用户和项目的数量,用户和项目之间的交互矩阵我们用Y∈oM×N来表示,矩阵中的隐式反馈数据定义如下:
(2)
式(2)中,y+表示交互矩阵中的正样本集合(用户和项目之间有交互),y-表示交互矩阵中的负样本集合(用户和项目之间没有交互)。由于我们提出的模型面向的是隐式反馈数据,所以处理数据集合的时候,对于用户u和项目i之间存在历史交互的数据,我们将yui值设为1,在某种程度上表明用户u对项目i感兴趣;反之,对于用户u和项目i之间无历史交互的数据,我们将yui值设为0,表示用户u对项目i不感兴趣。
从上述介绍的隐式反馈数据中学习出有用的经验,无疑是非常具有挑战性的。传统的方法是基于矩阵分解的协同过滤算法,该种方法还是受限于其中向量间的内积操作只能提取复杂历史交互中的线性特征信息。而我们提出的DeepCF-A是集成模型,线性特征提取部分延用了生成式矩阵分解模型;非线性特征提取部分采用了基于注意力机制的多层感知机模型(Multi-layer perceptron based on attention mechanism,MLP-A)。我们的模型能够有效地从隐式反馈数据中学习到有用的经验,从而帮助推荐系统提升推荐效果。
1.2 基于注意力机制的多层感知机模型
首先,我们提出的DeepCF-A模型的非线性特征提取模型,即基于注意力机制的多层感知机模型结构如图1。
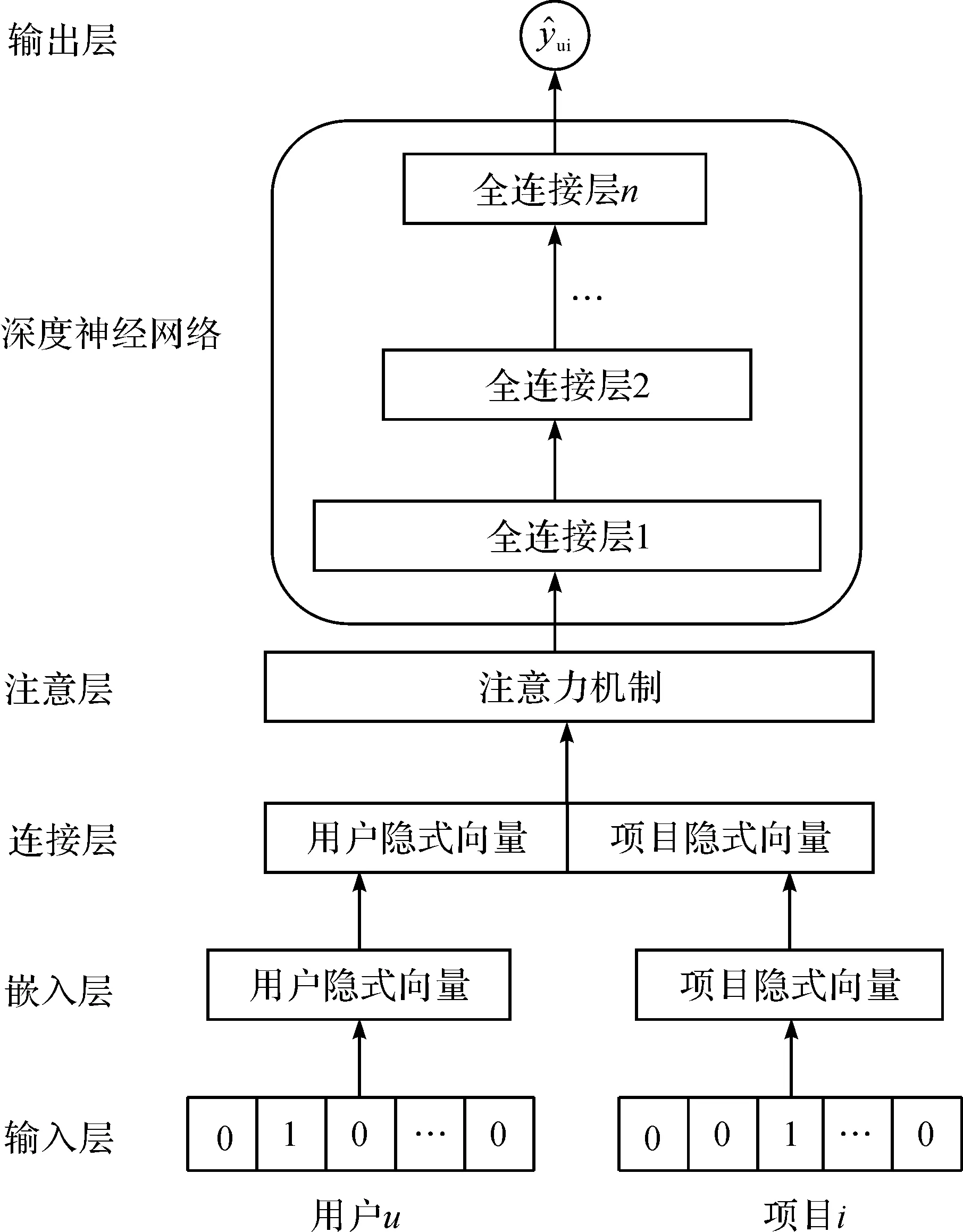
图1 基于注意力机制的多层感知机模型结构Figure 1 Multi-layer perceptron model structure based on attention mechanism
我们用vu和vi分别代表用户u和项目i的特征向量。输入层中,vu和vi均是one-hot的编码形式。这在一般的机器学习模型中也是比较常见的操作手段,利用one-hot编码对离散特征进行向量化的优点是让特征间的距离计算更加合理,也就是方便后续模型对数据进行特征提取。但是,当类别数量很多时,通过one-hot编码生成的特征空间会变得非常大,容易造成维度灾难。所以,我们引入了自然语言处理领域中处理词向量的word2vec方法,在输入层之上引入了嵌入层,成功地将输入层中稀疏的特征向量转换为稠密型的特征向量,从而有效缩减了特征空间的维度,更利于特征提取。连接层将嵌入层输出的用户隐式向量、项目隐式向量进行连接,并向注意层输出联合特征向量。
注意层利用注意力机制提取联合向量特征中对当前任务最为关键的特征信息,输出给深度神经网络。该层试图捕获特征向量中各维度特征之间的内在关系,每一维度特征对整个任务的影响程度都可能受到其他维度特征的影响。因此,对某些维度特征的过分关注可能会分散注意力,于是注意力机制就起到了至关重要的作用。注意力机制主要分为两步,第一步获取每个维度特征所对应的关注度。
An=Softmax(Xn)。
(3)
式(3)中,Xn表示输入注意层的n维特征向量,Softmax()函数可以通过归一化获取符合概率分布取值区间的注意力分配概率数值,An表示n个维度特征所对应的关注度。第二步,注意层将获取到的每个维度的关注度与特征向量对应维度相乘获得注意层的输出Aout:
Aout=An⊙Xn。
(4)
式(4)中,⊙为元素积操作,Aout用于输入深度神经网络中进行进一步的特征提取。

1.3 模型集成
上文中介绍了基于注意力机制的多层感知机模型,注重于提取用户和项目间历史交互数据中非线性交互特征。对于其中的线性交互特征的提取,我们用到了生成式矩阵分解模型。简单来说,生成式矩阵分解模型其实就是一般矩阵分解模型的泛化版本,其主要思想还是协同过滤。
综合生成式矩阵分解模型及基于注意力机制的多层感知机模型,我们提出了基于注意力机制的深度协同过滤模型。该模型的结构如图2。

图2 基于注意力机制的深度协同过滤模型结构Figure 2 Deep collaborative filtering model structure based on attention mechanism
整个模型的输入层将用户u和项目i的特征向量分别用one-hot编码表示。由于我们提出的模型是集成模型,所以嵌入层将one-hot编码表示的用户u特征向量分别映射为输入GMF模型的用户隐式向量及输入MLP-A模型的用户隐式向量。对于项目i同样如此操作。这样做的目的是,考虑到不同模型所需的特征空间大小不一,区分不同输入特征空间的做法更有意义。MLP-A模型已经详细介绍过,现在简单介绍一下GMF模型。
对于GMF模型部分,负责提取用户和项目间复杂历史交互数据中的线性特征。其中的关键操作就是将嵌入层输出的用户隐式向量和项目隐式向量做了一个十分简单的元素积操作,用于模拟基于矩阵分解的协同过滤算法,数学表达式可描述为
(5)

对于MLP-A模型部分,负责提取用户和项目间复杂历史交互数据中的非线性特征。其数学表达式如下:

(6)
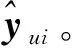
(7)
式(7)中,σ表示sigmoid函数。
我们提出的DeepCF-A模型的训练阶段选取的损失函数为交叉熵函数,其数学表达式如式(8):
(8)
训练阶段的目标是通过类似随机梯度下降方法,最小化损失函数,从而达到提升隐式反馈数据下推荐效果的目的。由于推荐系统领域内的用户-项目交互矩阵往往都是十分稀疏的,对于我们的目标来说,负样本的数量要远远大于正样本。所以,为了让模型的训练能够快速地收敛,我们采用了负采样的手段,即对负样本预先进行采样再用于模型的训练,这样做能够在不影响模型的性能前提下大大缩减模型训练时间。
2 对比实验
2.1 实验所用数据集合及评价标准
本文中实验所用数据集合均为公开数据集合,分别为Movielens和Pinterest。Movielens数据集是专门用来收集电影评分的,根据数据规模的不同,该数据集有很多版本。我们在这里选用的是Movielens-1M,所选用的数据集内包含有一百万例用户为电影评分的数据,其中评分数据均采用5分制,而且该数据集合保证每位用户至少参与20部电影的评分。Pinterest数据集是被用作图片推荐的,保留有用户对图片的评分数据。由于原始的Pinterest数据集中包含的数据过于稀疏,于是参考Movielens数据集,我们只保留了至少有20个历史评分的用户的数据。最终,实验所用的数据集合相关统计信息参考表1。
表1 实验所用数据集合相关统计信息
Table 1 Statistics related to the data set used in the experiment

数据集合交互数用户数项目数密度/%Movielens-1M1 000 2093 7066 0404.47Pinterest1 500 8099 91655 1870.27
由于我们提出的模型目标是提升隐式反馈数据下推荐系统的推荐性能,所以我们将数据集中的评分数据进行处理,将用户对项目有评分的交互数据标记为1,用户对项目未评分的交互数据标记为0。
模型训练过程中,我们从用户与项目历史交互数据中保留一项正样本留作模型评价,其他正样本连同负采样得到的负样本一同进行模型训练。在模型的评价阶段,我们随机抽取了99项负样本连同训练过程中保留的一项正样本构成集合,参与模型的评价。评价指标选用了HR@K(Hit ratio at rank k)和NDCG@K(Normalized discounted cumulative gain at rank k),均是评价隐式反馈数据下推荐算法性能的常用评价标准[13]。以上两种评价标准,HR@K表示只要有正样本出现在推荐算法推荐列表的前K位,就会给出得分。而NDCG@K则更加严格,会根据正样本出现在推荐列表的位置高低给出相应的得分,即排名越前得分越高。
2.2 模型参数设置
我们提出的DeepCF-A集成模型,其中MLP-A模型中的深度神经网络采用三隐藏层的结构,各层隐藏层节点个数设置遵循:前一层节点数为后一层节点数的2倍;嵌入层节点数为模型预测因子的2倍;除输出层激活函数使用sigmoid函数外,其他各层激活函数均使用ReLU函数。模型训练阶段,训练集构造依据:对于每1例正样本,通过负采样得到4例负样本一同参与模型训练;优化函数采用Adam函数,学习率设为0.001;训练迭代次数为40次。GMF模型部分嵌入层的特征空间大小设为8。
2.3 对比算法
为了验证我们提出的基于注意力机制的深度协同过滤模型在不同评价标准下的表现。我们同多种推荐算法进行对比,其中不仅包括了传统的推荐算法,同时也包括了基于深度学习的推荐算法。
ItemPop 该算法不属于个性化的推荐算法,仅仅基于项目的流行度(项目与用户历史交互的次数)来做推荐。
ItemKNN 该算法是标准的基于项目的协同过滤算法。对比实验过程中,我们测试了不同的参数值,最后取得最优的结果。
BPR 该算法是普通矩阵分解算法的优化版本,有着比普通矩阵分解算法更优的推荐性能,一般常用作基于隐式反馈数据的推荐算法的基准算法。
eALS 该算法是矩阵分解类算法的最优算法之一。
MLP 该算法利用了多层感知机取代矩阵分解类算法中的内积操作,提取用户和项目间复杂历史交互模式,用来做推荐。
MLP-A 该算法是我们提出的DeepCF-A模型中的,非线性特征提取模型,结合了深度学习中的注意力机制来做推荐。
NeuMF 基于深度学习的推荐算法,同样也是集成模型,推荐性能上较传统算法有很大提升。
2.4 实验结果分析
我们将DeepCF-A模型同上述提到的多种推荐算法在Movielens-1M和Pinterest数据集上进行了大量的对比实验。为了公平起见,对于有涉及模型预测因子的算法(BPR,eALS,MLP,MLP-A,NeuMF),我们将模型预测因子统一设为16。为了降低模型评价的时间复杂度,对于评价标准HR@K、NDCG@K中的K值,我们统一设为10。
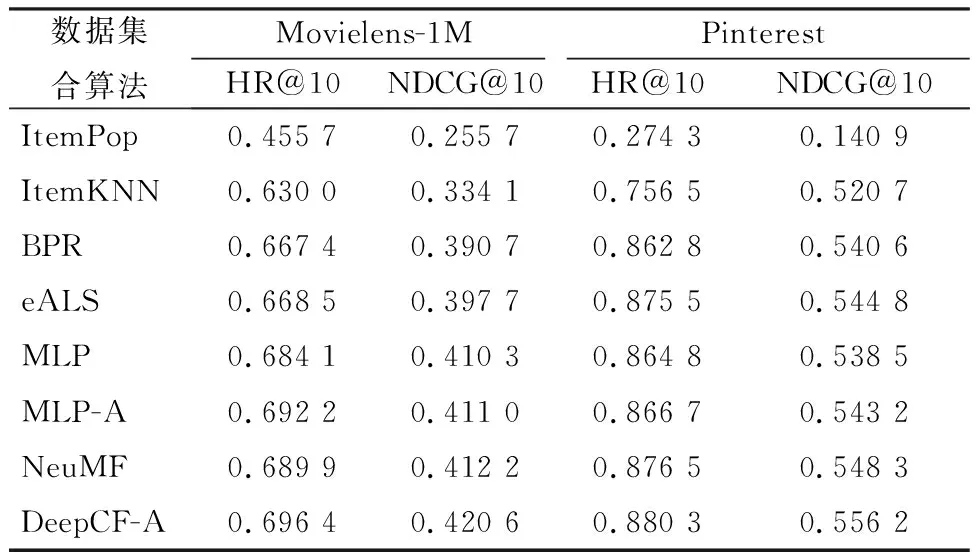
实验的结果由表2给出,图3图4向我们展示了不同算法在Movielens-1M数据集与Pinterest数据集上的表现。首先,从实验结果中我们可以直观地看到,不论是Movielens-1M数据集或是Pinterest数据集,我们提出的基于注意力机制的深度协同过滤模型在HR@10、NDCG@10评价标准下均表现最优。
表2 不同算法在Movielens-1M数据集和Pinterest数据集下的实验结果
Table 2 Experimental results of different algorithms in the Movielens-1M dataset and Pinterest dataset
数据集合算法Movielens-1MPinterestHR@10NDCG@10HR@10NDCG@10ItemPop0.455 70.255 70.274 30.140 9ItemKNN0.630 00.334 10.756 50.520 7BPR0.667 40.390 70.862 80.540 6eALS0.668 50.397 70.875 50.544 8MLP0.684 10.410 30.864 80.538 5MLP-A0.692 20.411 00.866 70.543 2NeuMF0.689 90.412 20.876 50.548 3DeepCF-A0.696 40.420 60.880 30.556 2
与传统的推荐算法(ItemKNN,BPR,eALS)进行比较,我们提出的DeepCF-A模型在Movielens-1M数据集下的HR@10指标上要高出它们3~6个百分点,同样在NDCG@10指标上要高出3~8个百分点。也就是说,我们提出的模型在隐式反馈数据下的推荐性能明显优于传统的协同过滤算法模型。
由于MLP模型与MLP-A模型的区别在于,MLP-A模型结合了注意力机制。从实验结果上来看,MLP-A模型较MLP模型在两个数据集上的HR@10与NDCG@10均有所提升。故注意力机制确实能帮助一般的深度神经网络更好地提取复杂的数据中更为关键的特征信息。
与DeepCF-A模型一样,NeuMF模型也是集成模型。从实验结果上分析,集成模型确实较单个模型表现更优。与NeuMF模型相比,在Movielens-1M数据集下我们提出的模型在HR@10与NDCG@10指标上分别高出一个百分点,在Pinterest数据集上的表现同样类似。
3 结 论
本文中,我们将深度学习技术用于增强传统推荐系统领域中协同过滤算法的性能,提出了基于注意力机制的深度协同过滤模型。该模型是集成模型,具备深度提取用户和项目间复杂历史交互数据中线性、非线性的特征的能力,能够有效在隐式反馈数据下给出高质量的推荐内容。我们在Movielens-1M和Pinterest数据集下进行了大量的实验,实验结果充分证明我们所做的工作是十分有效的,我们提出的模型无论较传统的协同过滤模型,还是当前推荐系统领域基于深度学习的推荐模型,在推荐性能上均有显著提升。

图3 各个算法在Movielens-1M数据集和Pinterest数据集下的表现Figure 3 Performance of each algorithm in the Movielens-1M dataset and Pinterest dataset

