圆柱齿轮分扭传动系统的均载特性及试验研究

靳广虎，龙珊珊，高鹏，潘磊，朱如鹏

(南京航空航天大学直升机传动技术重点实验室，江苏南京，210016)

开展新型传动构型研究、提高功重比和功率密度是直升机主减速器传动系统的重要研究热点之一。20世纪70年代，WHITE[1-3]针对圆柱齿轮分扭传动系统开展了一系列研究，发现与行星齿轮传动系统相比，采用圆柱齿轮分扭传动系统具有最后一级减速比大、传动级数少、质量小、支承简单、传动效率和可靠性高等优点。对分扭传动构型来说，2个分支传递的载荷要相等，否则将发生偏载，承载过大的分支甚至会发生断齿，影响传动系统的安全和使用寿命。可见，传动系统的均载性能是分扭传动构型的重要研究内容之一。为提高传动系统的均载和动力学性能，国内外学者开展了广泛研究。KISH[4]提出采用含弹性材料的齿轮腹板结构，通过弹性材料的较大阻尼来提高传动系统的动力学特性及均载性能。但是，受传动系统引起的温度影响，该方法有较大局限性。MAJID[5-6]等提出采用平衡梁法实现均载。但是采用平衡梁法并不是一个有效的措施，除非其摩擦因数小于0.003。为此，KRANTZ等[7-10]提出采用同步角的设计方法来实现均载，其主要思想是：通过精确的理论计算和分析，获得实现2个分支均载要求的轮系偏转角，然后采用预制轮系间的安装角度差来实现载荷均等。该设计方法不仅对传动系统的制造和安装误差要求很高，而且需精确计算出传动系统的零部件变形。为进一步提高分扭传动系统的工程应用可行性，WHITE等[11-12]提出采用柔性轴套的方法，运用柔性轴产生的大变形来协调2个分支间的载荷，从而优化传动系统的均载特性。目前，采用弾性轴实现均载的设计方法已应用于CH53E 重型直升机主减速，并通过耐久性试验验证。鉴于圆柱齿轮分扭传动系统在直升机主减速器传动系统中的广阔应用前景，杨振等[13-19]等对圆柱齿轮分扭传动系统的动力学、配齿及均载性能的敏感性影响参数等进行了研究，并取得一定的研究成果。针对圆柱齿轮分扭传动系统，圆柱齿轮分扭传动的均载性能试验研究还鲜见报道。为此，本文以单输入圆柱齿轮分扭传动系统为对象，建立含齿面摩擦的传动系统动力学模型和动力学方程；根据理论分析，重点研究和分析扭转刚度的变化对传动系统均载性能的影响，并开展理论与试验对比分析。

1 动力学模型

图1所示为单输入圆柱齿轮分扭传动系统的结构示意图。其工作原理为：系统的输入功率由输入齿轮Zp分2 路传递至分扭级齿轮ZLs和ZRs，再经左右分支并车级齿轮ZLh和ZRh将功率汇流传递至输出大齿轮ZB。图中，字母L和R分别表示左、右分支零部件。

图2所示为单输入圆柱齿轮分扭传动系统的动力学模型。各构件的刚度、阻尼和传递误差分别用字母K，c和e并配合相应的下标表示。单输入圆柱齿轮分扭传动系统的自由度共16个，可用矢量Y表示为：

图1 单输入圆柱齿轮分扭传动系统示意图Fig.1 Diagram of single input gear split torque transmission

式中：φD和φp分别为输入构件和输入齿轮的扭转微位移；φRs，φLs，φRh和φLh分别为分扭级和功率汇流级齿轮的扭转微位移；φB和φo分别为输出齿轮和输出构件的扭转微位移；Xp和Yp分别为输入轴的横向和纵向微位移；XR和YR分别为右双联轴的横向和纵向微位移；XL和YL分别为左双联轴的横向和纵向微位移；XB和YB分别输出轴的横向微位移和纵向微位移。

由于传动系统存在多对齿轮副同时啮合，为便于推导传动系统的动力学方程以及开展动力学特性的分析，引入2种坐标来描述，即广义坐标系和局部坐标系。图3所示为传动系统的局部坐标和广义坐标关系图。图3中上标带*号的表示局部坐标；坐标系中的Y和Y*方向沿各齿轮副的啮合线方向；坐标原点为相应齿轮的转动中心。广义坐标和局部坐标间的关系可表示为[20]

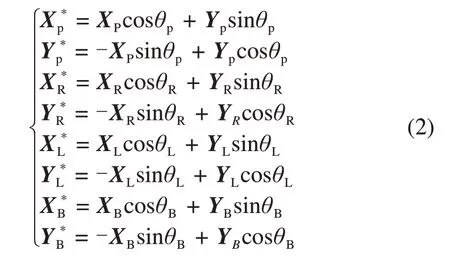
式中：θp，θR，θL和θB分别为Yp与Y*p，YR与Y*R，YL与Y*L以及YB与Y*B之间的夹角。

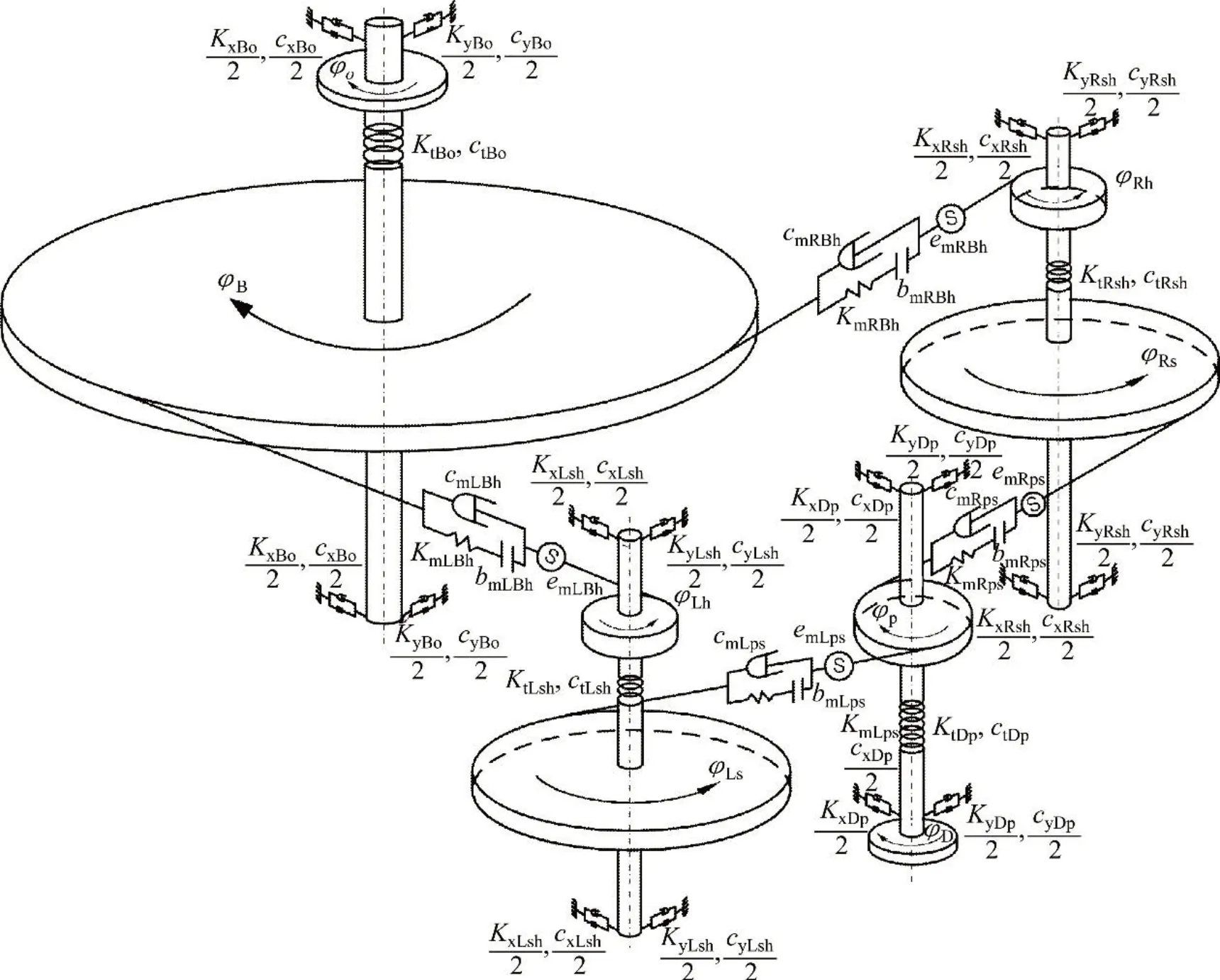
图2 单输入圆柱齿轮分扭传动系统的动力学模型Fig.2 Dynamic model of single input gear split torque transmission

图3 局部和广义坐标关系图Fig.3 Relation between local and generalized coordinate system

2 动力学微分方程

2.1 角位移与线位移之间的关系

由图3可知：传动系统中齿轮副啮合线方向的综合位移表达式为

式中：YmRps，YmLps，YmRBh和YmLBh分别为齿轮Zp与齿轮ZRs，齿轮Zp与齿轮ZLs，齿轮ZRh与齿轮ZB以及齿轮ZLh与齿轮ZB沿啮合线方向的综合位移；rbp，rbRs，rbLs，rbRh，rbLh和rbB分别为齿轮Zp，ZRs，ZRh，ZLs，ZLh和ZB的基圆半径；emRps和emLps分别为Zp与ZRs和Zp与ZLs相应啮合齿轮副间的传递误差；emRBh和emLBh分别为ZB与ZRh和ZB与ZLh啮合齿轮副间的传递误差。

式(1)中同时存在线位移和角位移，为便于方程的求解，将角位移转化为线位移，则得

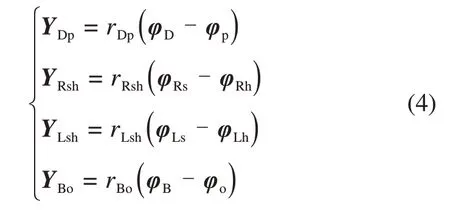
式中：YDp，YRsh，YLsh和YBo分别为输入轴、右分支双联轴、左分支双联轴和输出轴的扭转线位移；rDp，rRsh，rLsh和rBo分别为各传动轴的等效半径。

2.2 传动系统受力分析

传动系统中的人字齿轮采用双斜齿表示，则圆柱齿轮分扭传动系统齿轮副间的啮合力可表示为

式中：FmLps，FmLBh，FmRps和FmRBh分别为齿轮ZLs与Zp，ZLh与ZB，ZRs与Zp和ZRh与ZB之间的动态啮合力。K和c配合下标分别表示相应齿轮副间的啮合刚度和阻尼。各传动轴沿X和Y方向上所受的合力为：

式中：Fxp与Fyp分别为输入轴沿相应的广义坐标X和Y方向所受的合力；FxR与FyR分别为右分支双联轴沿相应的广义坐标X和Y方向所受的合力；FxL与FyL分别为左分支双联轴沿相应的广义坐标X和Y方向所受的合力；FxB与FyB分别为输出轴沿相应的广义坐标X和Y方向所受的合力。传动系统中，啮合齿面间会产生齿面摩擦力，各级齿轮齿面间的摩擦力可表示为

式中：fmRps，fmRBh，fmLps和fmLBh分别为齿轮Zp与ZRs，齿轮ZRh与ZB，齿轮Zp与ZLs以及齿轮ZLh与ZB间的齿面摩擦力；umRps，umRBh，umLps和umLBh分别为相应啮合齿轮副之间的时变摩擦因数。时变摩擦因数μ为[21]：

式中：Ph为最大赫兹应力；ν0为润滑油动力学黏度；S为表面粗糙度均方根；ve为接触齿面的卷吸速度；R为接触齿面的综合曲率半径；b1，b1，…，b9为计算参数[22]。则传动轴上沿广义坐标X和Y方向上所受摩擦力的合力为：

式中：fxp与fyp输入轴沿相应广义坐标X和Y方向所受的摩擦力合力；fxR与fyR分别为右分支双联轴沿相应广义坐标X和Y方向所受的摩擦力合力；fxL与fyL分别为左分支双联轴沿相应广义坐标X和Y方向所受的摩擦力合力；fxB与fyB分别为输出轴沿相应广义坐标X和Y方向所受的摩擦力合力。

2.3 动力学平衡方程

根据以上的理论分析，图2所示的传动系统动力学微分方程可表示为：

式中：mD和mO分别为输入端和输出端的质量；mp，mRs，mRh，mLs，mLh和mB分别为Zp，ZRs，ZRh，ZLs，ZLh和ZB的质量；ID和IO分别为输入端和输出端的转动惯量；Ip，IRs，IRh，ILs，ILh和IB分别为输入端；Zp，ZRs，ZRh，ZLs，ZLh和ZB和输出端的转动惯量；rrRp和rrRs分别为fmRps对齿轮Zp和ZRs的摩擦力臂；rrLp和rrLs分别为fmLps对齿轮Zp和ZLs的摩擦力臂；rrRh和rrRB分别为fmRBh对齿轮ZRh和ZB的摩擦力臂；rrLh和rrLB分别为fmLBh对齿轮ZLh和ZB的摩擦力臂。

2.4 均载系数的计算

传动系统的动力学微分方程采用Runge-Kutta法求解。通过求解方程，获得传动系统各个自由度的振动响应。在分流级齿轮传动的每个周期内，左、右分支双联轴上的动态扭矩TLsh，TRsh定义为

式中：KtLsh和KtRsh分别为左、右双联轴的扭转刚度；ΔφLsh和ΔφRsh分别为左、右双联轴的扭转角位移。则左右分支任意时刻的均载系数bLsh(t)和bRsh(t)可表示为

令ΩLsh和ΩRsh分别为左右分支动态均载系数的最大值，则圆柱齿轮分扭传动系统的均载系数Ωsh定义为

3 动力学均载特性

3.1 均载系数

图4所示为分扭传动系统左右分支均载系数的时域变化图。由图4可知，右分支均载系数小于左分支均载系数。研究结果表明：尽管传动系统具有几何对称性，但是齿轮承受的载荷并不对称，从而导致两分支齿轮副间的中心距出现差异，使得齿轮转角位移不同，因此，右分支的均载系数较小。

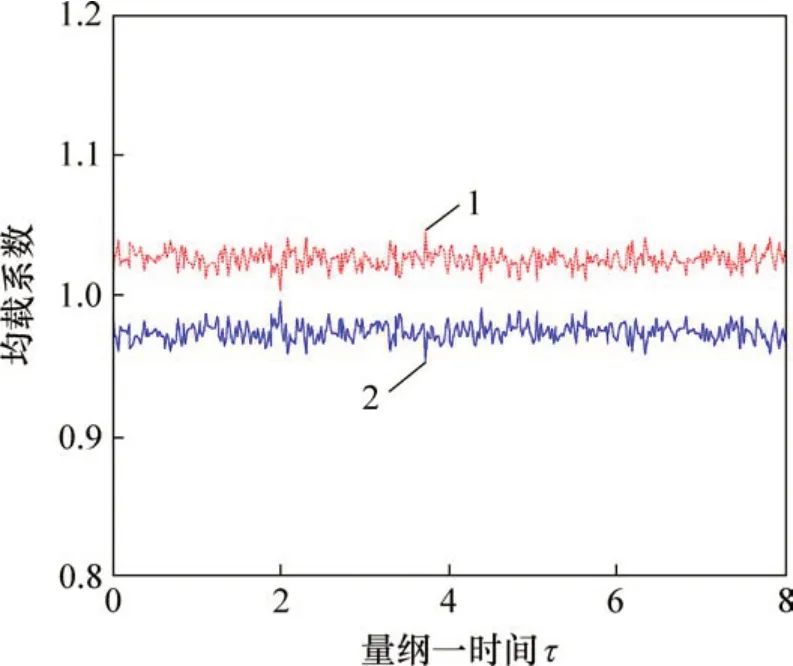
图4 均载系数的时域变化图Fig.4 Time domain diagram of load sharing coefficient

3.2 扭转刚度对均载系数的影响

图5所示为双联轴扭转刚度对均载系数的影响。由图5可知：增大双联轴扭转刚度，动态均载性能变差。主要原因为：当双联轴扭转刚度增大时，其在整个系统中的变形量比重减小，从而降低补偿齿轮副中心距位移、齿轮侧隙等引起的系统偏转角的能力，导致均载系数增大。因此，要提高传动系统的均载性能，在满足传动轴强度的条件下，可采用柔性轴的设计方法。

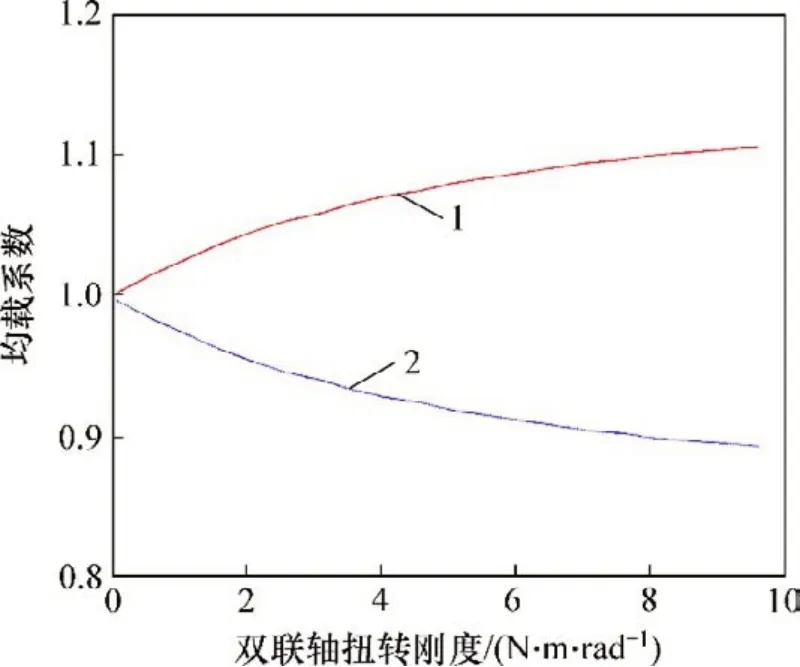
图5 双联轴扭转刚度对均载系数的影响Fig.5 Influence of torsional stiffness of duplicate shaft on load sharing coefficient

图6所示为输入、输出轴扭转刚度对均载系数的影响。研究结果表明：影响均载性能的主要因素为啮合齿轮副中心距变化的微位移以及齿侧间隙，而输入轴和输出轴扭转刚度变化所引起的扭转变形对齿轮副中心距变化的微位移影响很小。因此，传动系统的均载系数基本没变化。

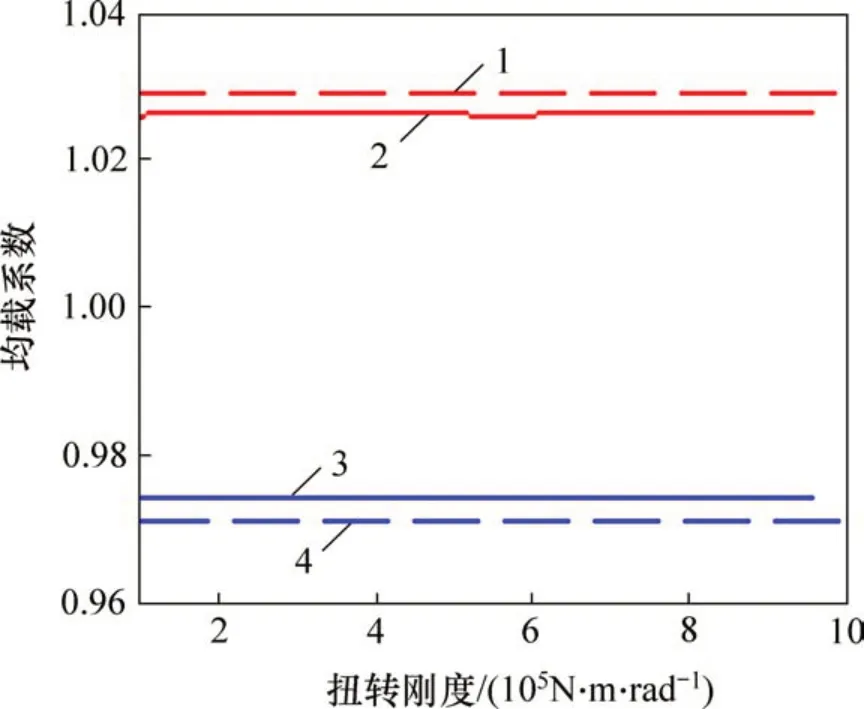
图6 输入、输出轴扭转刚度对均载系数的影响Fig.6 Influence of torsional stiffness of input and output shaft on load sharing coefficient

4 动力学均载性能试验验证

为验证理论分析的正确性，以体积最小为优化目标，开展圆柱齿轮分扭传动系统的参数优化设计，研制分扭传动试验台，并开展传动系统的动力学均载性能试验验证。根据理论分析，重点研究双联轴的柔性对传动系统均载性能的影响，并开展均载系数的试验值和理论值的对比分析。优化后的传动系统基本参数如表1所示。

表1 单输入圆柱齿轮分扭传动系统的主要参数Table 1 Main parameters of single input gear split torque transmission

传动系统中的齿轮副满足同步啮合条件，因此相应齿轮副之间的啮合刚度同步变化。分扭级齿轮副的平均啮合刚度为6.08×108N/m，并车级齿轮副的平均啮合刚度为1.24×109N/m；轮齿啮合的阻尼比取0.13，其计算方法参考文献[23]。输入轴沿X和Y方向的支撑刚度为4.27×108N/m，分扭传动轴沿X和Y方向的支撑刚度为8.45×108N/m，输出轴沿X和Y方向的支撑刚度为1.38×109N/m。分扭级齿轮副中心线之间的安装角θp=160°，并车级齿轮副中心线之间的安装角θR=60°。分流级齿轮副的齿侧间隙为250um，并车级齿轮副的齿侧间隙为300μm。

4.1 试验装置与方案

图7所示为单输入圆柱齿轮分扭传动系统试验台实物图，图8所示为2组双联轴的结构图。通过双联轴内部嵌套柔性轴的设计方法，提高整个轴的柔性。其中，第2 组双联轴扭转刚度小于第1 组扭转刚度。通过应变传感器及其遥测系统，应用江苏东华测试技术股份有限公司DH5922动态信号测试分析系统进行数据的采集与后处理，在该试验台上开展了2组3个工况下的试验测试，获得传动系统的均载系数。3种工况试验参数如表2所示。

4.2 双联轴扭矩的标定

图7 单输入圆柱齿轮分扭传动系统试验台实物图Fig.7 Tester for single input gear split torque drive system

图8 双联轴的结构示意图Fig.8 Diagrams of duplicate shaft

表2 3种工况的试验参数Table 2 Test parameters for three operating conditions

图9 双联轴扭矩标定实物图Fig.9 Torque calibrations of duplicate shaft

为获得双联轴的扭矩便于开展传动系统的均载系数试验验证，需确定双联轴的实际扭矩和应变片所测量的实测扭矩之间的关系，因此，需要标定双联轴。图9所示为双联轴扭矩标定实物图。本试验应用电阻应变片、采用全桥测量法获得双联轴的扭矩。按照贴片要求，在双联轴外表面黏贴电阻应变片，导线从中空的轴中引出，实物如图9(a)所示。标定的原理为：固定双联轴的一端，在双联轴的另一端通过加载装置(加载实物如图9(b)所示)施加扭矩。施加的实际扭矩可通过计算获得，双联轴的实测扭矩由应变片测量获得。通过对实际扭矩和实测扭矩进行处理从而得到两者之间的关系。

标定的主要过程为：1)标定前，敲击各传动轴，使齿轮脱离接触；2)将砝码按顺序依次放置于砝码盘上，并保持15 min。每加1 次砝码，记录1 次角度仪与砝码数据，进而获得实际扭矩；同时，记录采集装置采集到的应变片实测扭矩；3)采用最小二乘法对实际扭矩和实测扭矩进行二次曲线拟合，获得实际扭矩和实测扭矩之间的关系。根据上述原理与方法，获得实测扭矩和实际扭矩关系曲线。2组实测扭矩和实际扭矩的关系曲线如图10所示。

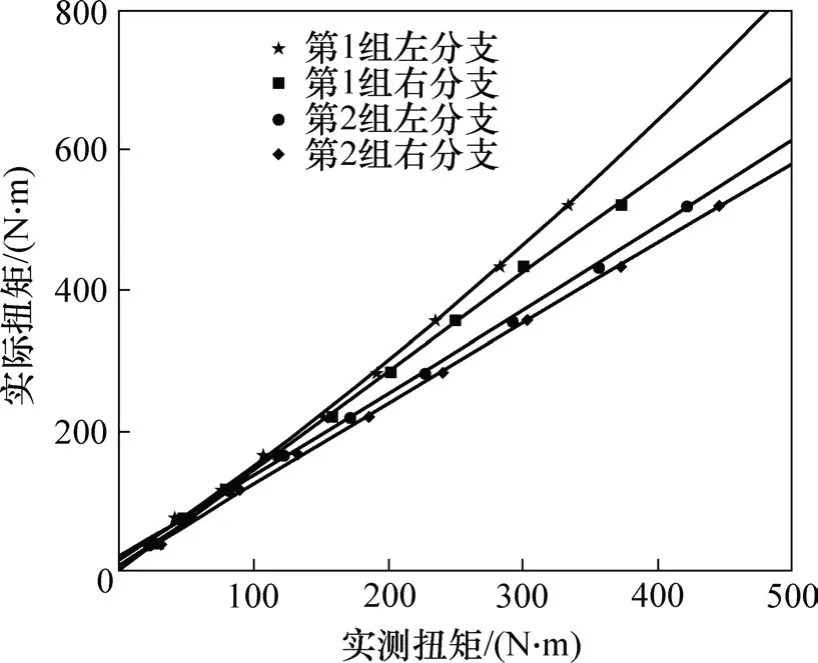
图10 双联轴的实测扭矩和实际扭矩曲线图Fig.10 Curve of measured torque and actual torque of the duplicate gear shaft

4.3 试验结果分析

第1 组试验测得3 种工况下左、右分支双联轴的扭矩如图11所示。根据获得的实测扭矩和实际扭矩的拟合曲线，将图11的数据转化为双联轴上的实际扭矩，再根据均载系数的计算方法，可获得3种工况下左右分支的均载系数。第1组3种工况下获得的均载系数试验值与理论值的对比如表3所示。由表3可知：在3种工况下，均载系数的试验值与理论值的相对误差均小于10%。第1 组双联轴在3 种工况下获得的均载系数试验值和理论值如图12所示。

第2 组双联轴在3 种工况下获得的均载系数试验值和理论值如图13所示；均载系数的试验值和理论值的对比分析如表4所示。由表4可知：在3 种工况下，均载系数试验值和理论值的误差均小于10%。2组均载系数试验值与理论值之间的相对误差表明，传动系统的动力学分析模型具有可靠性。

图11 第1组左右分支双联轴实测扭矩Fig.11 Measured torque of the left and right branch of duplicate shaft of first set

表3 第1组均载系数理论与试验值对比Table 3 Comparison of theoretical and experimental load sharing coefficient of the first set of tests

图12 第1组传动系统均载系数Fig.12 Load sharing coefficient of the first set under three operating conditions

表4 第2组均载系数理论与试验值对比Table 4 Comparison of theoretical and experimental load sharing coefficien of the second set of tests

表5所示为2 组均载系数的试验结果对比。由表5可知：在相同工况下，双联轴扭转刚度的减小，增大传动轴的柔性，其补偿传动系统的变形能力增大，因此，传动系统左右分支的均载性能提高。就每组试验的结果来看，均载系数的变化规律也趋于一致。其中，第2 组工况2 下的均载性能最好。研究结果表明：在分扭传动系统中，不仅要注重双联轴扭转刚度的参数匹配设计，还要优化设计齿轮副间的齿侧间隙，从而降低传动系统的振动，获得较好的均载性能。

图13 第2组的传动系统均载系数Fig.13 Load sharing coefficient of the second set

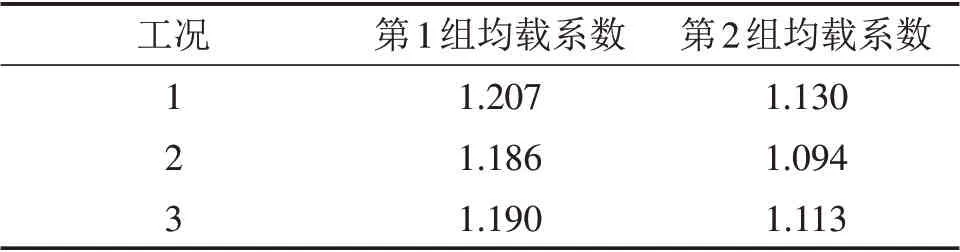
表5 均载系数的试验结果对比Table 5 Comparison of experimental data of load sharing coefficient between two sets

5 结论

1) 减小双联轴扭转刚度，可有效补偿齿轮副中心距变化的微位移、齿轮侧隙等引起的系统偏转角，改善传动系统的均载性能；输入轴和输出轴扭转刚度的变化对左右分支齿轮副中心距变化的微位移补偿无实质性影响。

2)2组参数获得的均载系数试验值和理论值之间的相对误差均小于10%。在相同工况下，第2组均载系数的试验值比优于第1组的低，该试验结果验证了理论研究模型和分析方法的有效性。

3) 为降低圆柱齿轮分扭传动系统的均载系数，在满足双联轴的强度前提下，可采用较大的柔度。