考虑弹簧应力松弛的高压断路器运动特性

黎小峰，巫世晶，李小勇,2，赵灯，李巧全，李星

(1.武汉大学水射流理论与新技术湖北省重点实验室，湖北武汉，430072；2.武汉大学苏州研究院，江苏苏州，215123；3.烽火通信科技股份有限公司，湖北武汉，430205)

高压断路器是高压电力输送体系中重要的控制和保护设备，其主要功能是在收到控制信号时及时可靠地分合闸动作，完成电路的切断和接通，其运行状态直接影响整个电力系统的稳定性和可靠性[1]。高压断路器在分合高压线路时，动静触头间会产生高温高压电弧。如果分合闸时间长于断路器分合闸安全操作技术标准，或在规定时间内动、静触头分合不彻底，会造成触头熔焊，线路烧毁等故障。高压断路器分合闸动作由内部的操动机构驱动，按照动力源的不同可分为电磁操动机构、弹簧操动机构、气动操动机构及液压操动机构等。其中弹簧操动机构因其操作灵活，不存在漏油和漏气等优点，在10～35 kV 电压等级的高压断路器中被广泛采用[2]。作为弹簧操动机构核心部件的分合闸弹簧为断路器的分合闸运动提供驱动力，其性能关系到断路器分合闸动作可靠性[3-4]。高压断路器一般只在线路故障以及检修时才进行分合闸动作，其操动机构动作不频繁甚至常年不动。分合闸弹簧长期处于静止的伸长状态，会发生过程缓慢且难以被直观监测的应力松弛现象，致使弹簧操动机构驱动力不足，最终导致断路器无法正常分合闸动作，严重影响电力系统的安全运行。高压断路器分合闸的灭弧过程对动触头速度要求极高，而应力松弛将导致弹簧弹性消退，降低分合闸操动功，给分合闸运动带来不利影响[5]。国内外学者通过对比合金试件在蠕变前后的微观金相组织结构以及金属微观组织在蠕变过程中的演变规律，对蠕变和应力松弛的机理展开了深入研究[6-9]。根据以往的研究，蠕变是材料内部位错运动及重新排列，使得组织趋向于均匀化、稳定化的过程，且呈现三阶段特征[10-12]。封先河[13]将蠕变过程中的可动位错视为获得足够能量的活化粒子，从能量的角度推导了弹簧的蠕变动力学方程，并对所研究弹簧寿命进行了评估。所推导的弹簧蠕变动力学方程中的未知参数较多，需要通过多组不同温度下的弹簧蠕变试验才能最终确定，限制了其使用。应力松弛机理与蠕变微观机理相同，但表现形式不同，应力松弛是固定形变条件下应力降低，蠕变是高应力条件下部分弹性应变转变为不可恢复变形的形变过程，二者数值可以相互转换，亦有学者深入研究了应力松弛和蠕变之间的数值转换关系，指出了通过短期应力松弛试验数据获得弹簧蠕变本构模型中未知参数的方法[14-17]。国外有学者建立了弹簧的应力松弛有限元模型，并对影响应力松弛速率的温度、载荷、材料等因素展开了进一步研究[18-19]。以上研究者多采用试验研究手段，对应力松弛与蠕变的发生机理、影响因素以及二者之间的数值转换进行了研究，而关于弹簧应力松弛对高压断路器分合闸运动的影响研究较少。有研究者通过仿真研究指出，分合闸弹簧是高压断路器机械故障的敏感因素，弹簧应力松弛对高压断路器分合闸运动特性的影响不可忽略[20]。本文作者选用Norton蠕变本构模型研究ZN12型高压断路器分合闸弹簧的应力松弛问题。该本构模型忽略温度对蠕变速率的影响，未知参数较少，适合于户内高压断路器分合闸弹簧的研究。通过短期应力松弛试验获得本构模型中的未知参数，并求解弹簧服役后期的应力松弛结果。最后采用机械动力学仿真软件ADAMS研究分合闸弹簧应力松弛对该型断路器分合闸运动特性的影响。

1 断路器操动机构简介

ZN12 型高压真空断路器为三相交流50 Hz 的户内高压开关，具有开断能力强和操作功能齐全等优点，在电力系统中应用广泛。图1所示为该型高压断路器的某一相弹簧操动机构结构示意图，该弹簧操动机构由一组多连杆机构和分合闸弹簧组成，连杆之间通过铰接副连接(图1中A，B，C，D，E，F和G处)。传动机构内安装有3种不同尺寸圆柱螺旋弹簧，分别为合闸弹簧、分闸弹簧和触头弹簧，弹簧材料均为60Si2Mn。其中触头弹簧为压缩弹簧，仅起到缓冲作用，不作为本文的研究重点。本文所研究的分合闸弹簧均为拉伸弹簧，弹簧参数如表1所示。

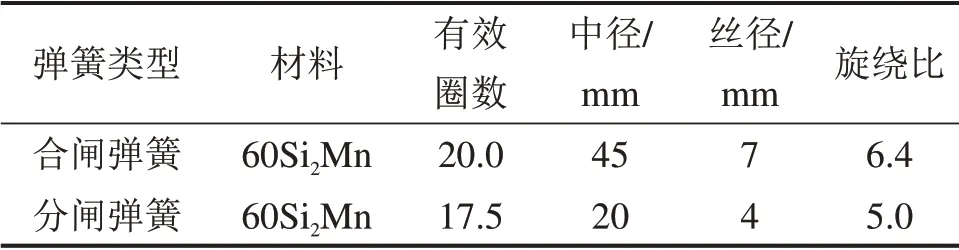
表1 ZN12高压断路器弹簧基本参数Table 1 Basic parameters of spring for ZN12 high voltage circuit breaker

高压断路器在收到合闸信号时，处于伸长状态的合闸弹簧10释放并带动凸轮1顺时针旋转。凸轮撞击连杆2；连杆2 在受拉凸轮1 的作用下，通过连杆机构的传动，驱动动触头向上运动，最终与静触头9抱合完成合闸动作。同理，高压断路器在收到分闸信号时，伸长状态的分闸弹簧11 释放，驱动下拐臂顺时针旋转；动触头8 向下运动促使动触头8 和静触头9分离完成分闸动作。

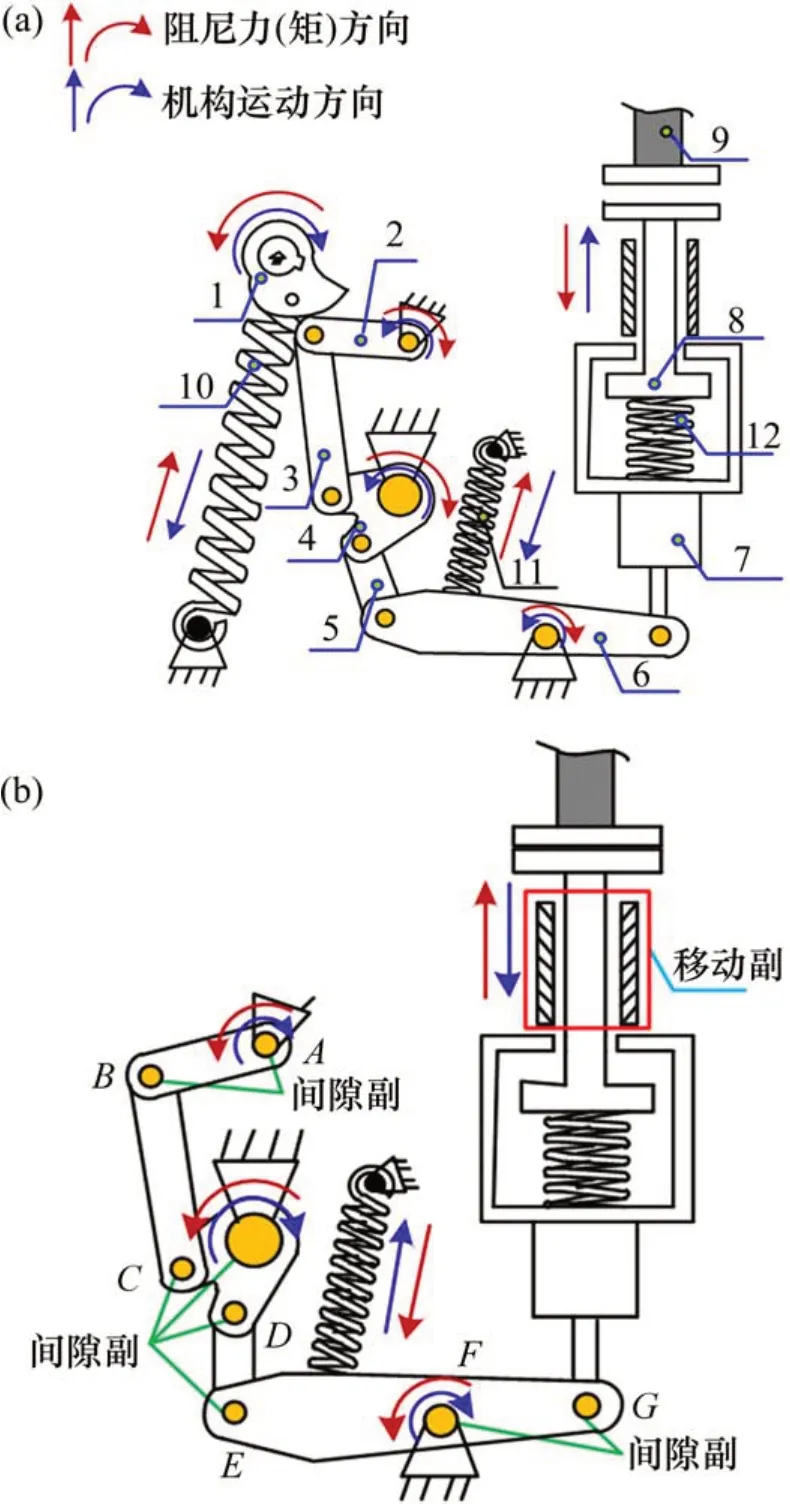
图1 ZN12型高压断路器弹簧操动机构原理图Fig.1 Schematic diagram of spring operating mechanism ofhigh voltage circuit breaker

2 断路器仿真模型建立与验证

2.1 仿真模型建立

对于简单机构如四连杆机构和曲柄滑块机构，基于牛顿定理和拉格朗日方程，通过建立机构的动力学微分方程组进行求解，能够得到机构的动力学输出特性[21-22]。然而，高压断路器系统结构复杂，直接建立动力学方程组并进行数值求解其动触头的时间-位移曲线较困难，且难以同时考虑运动副的接触，导致计算结果误差较大[23]。机械动力学仿真软件ADAMS基于拉格朗日方程和虚功原理，能够准确建立断路器的实体模型并分析断路器动力学状态。本文以ZN12型高压断路器为研究对象，在ADAMS下建立该型高压断路器的动力学仿真模型，研究弹簧应力松弛对高压断路器分合闸运动特性的影响，建模过程如图2所示。

主要建模过程如下。

1) 设置工作环境和材料属性。在ADAMS/View中导入操动机构三维模型后，调整工作网格、重力加速度方向以及坐标轴等工作环境，同时把相互之间没有相对运动的构件耦合固定联接，以减少模型构件数目，并对简化后模型的构件重命名及定义其材料属性。

2) 添加约束副。为构件定义材料属性后，再定义各构件之间的相对位置和相对运动方式，即对模型添加约束，将各构件联接，使其组成一个机械系统，模拟机械的实际运行状况。将高压断路器存在碰撞的构件之间采用接触进行联接，其余构件均采用ADAMS提供的约束副联接。

3) 施加力与载荷。根据前述机构的工作原理可知，操动机构的动力元件为弹簧，因此，在模型中施加的力主要为弹簧力，包括压缩弹簧、拉伸弹簧，其中，分合闸弹簧为拉簧，触头弹簧为压簧。通过以上步骤即完成操动机构动力学仿真模型的前处理工作，所建立的弹簧操动机构分合闸仿真模型如图3所示。

4) 设置求解器。高压断路器仿真模型中包含力与碰撞等动力学问题，因此，选择动力学求解器，其积分器为常用的GSTIFF积分器、积分格式选择求解精度较高的SI2积分格式、积分误差降低至系统默认误差的下一数量级即10-4。取合闸仿真时间为0.04 s，步数为600 步；分闸仿真时间为0.03 s，步数为500步。

2.2 试验验证

高压断路器分合闸过程中，动触头时间、位移是最重要的参数，是弹簧操动机构作用下的最终输出性能指标，是决定动触头和静触头能否可靠开断、关合的关键。只有在规定的时间内完成充分的分合闸运动，才能实现可靠的灭弧，实现高压输电线路的开断与关合。本试验测量该型断路器操动机构的输出端动触头时间、位移，并与仿真结果进行对比验证，所搭建的试验测试系统如图4所示。仿真模型对高压断路器本体进行了一定简化，且设置的仿真参数与真实断路器工况存在一定误差，所建立的仿真模型需要通过分合闸试验进行进一步验证。

图2 高压断路器仿真建模流程图Fig.2 Flow chart of simulation modeling for high voltage circuit breaker

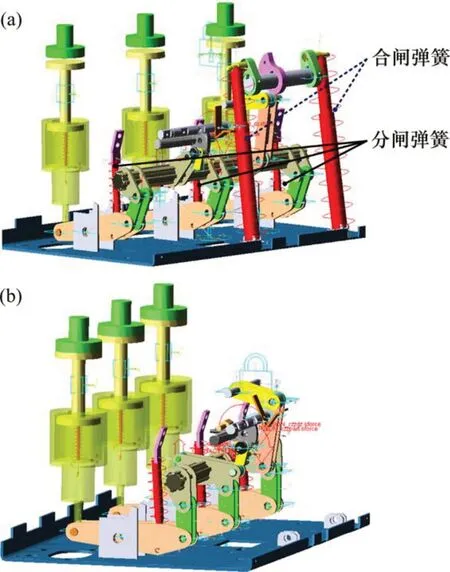
图3 ZN12高压断路器仿真模型Fig.3 Simulation models of ZN12 high voltage circuit breaker

在该分合闸试验中，首先通过固定支架将高压断路器支起在断路器底部，将位移、速度传感器固定安装于辅助支撑上，该辅助支撑与支架固定。在断路器机架底部上开孔并通过连接套筒，将传感器的测量头与高压断路器操动机构的动触头相连，实现对动触头的位移测量。所得输出端的分合闸位移曲线如图5所示。

从图5可以看出：高压断路器仿真位移曲线与试验测试位移曲线趋势基本一致，但因仿真模型存在一定简化，所以，无法完全准确模拟机构运动过程中的摩擦力等阻力，导致合闸运动后期的仿真曲线的上升趋势略快于试验曲线的上升趋势。从图5还可以看出：试验所得位移曲线波动较大，这是试验误差和机构本身性能退化所导致。合闸位移曲线在t=0.023 s发生最大偏离，仿真结果与试验结果的相对误差为5.7%，分闸位移曲线在t=0.009 s 发生最大偏离，仿真结果与试验结果的相对误差为6.4%，仿真和试验所得位移曲线的相对误差均控制在10%以内。当分合闸运动完成时，合闸仿真与试验位移终点分别为12.1 mm 和12.0 mm，完成时间均为23.5 ms；分闸仿真与试验位移终点分别为12 mm，完成时间均为21 ms，仿真结果与试验结果总体吻合程度较高，且运动行程和时间均符合该型高压断路器的技术标准。由此可知：在ADAMS中所建立的高压断路器仿真模型具有较高的准确度，能够真实模拟实际机构的运动过程。

图4 断路器分合闸试验系统Fig.4 Operation experiments for circuit breaker

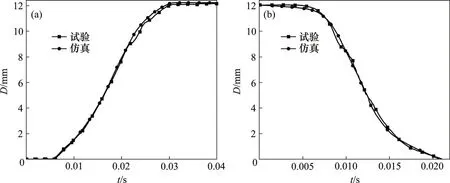
图5 动触头位移曲线Fig.5 Displacement curves of moving contact

通常高压断路器产品在设计、制造、装配完成后，弹簧操动机构动触头时间、位移也是确定的。然而，在断路器服役过程中，分合闸弹簧不可避免地会发生应力松弛，使得分合闸过程中的动触头的时间-位移曲线受到影响。当合闸完成时间超过规定的临界阈值的下限时，合闸运动会出现慢合故障，即在要求合闸时间阈值区间范围不能实现电路电流的接通，从而增加合闸过程的预击穿时间，有可能导致触头熔焊现象。而当分闸速度超过临界阈值的下限时，分闸运动会出现慢分故障，短路电流导致燃弧时间的增加造成触头烧毁。为此，深入研究高压断路器分合闸应力松弛问题可以提高断路器产品可靠性，以便对断路器操动机构的设计和产品检修提供理论指导。

3 分合闸弹簧应力松弛参数研究

3.1 弹簧蠕变本构模型

弹簧蠕变过程中，温度是影响弹簧蠕变的重要因素，蠕应变速率与弹簧所处温度及应力正相关[24]。考虑本文研究的ZN12高压断路器为变电站户内高压断路器，其分合闸弹簧服役环境温度为室温，温度变化较小，故本文将温度看作常数，采用下式所示Norton蠕变本构模型研究弹簧应力松弛现象：

式中：为蠕应变速率；A为与材料和微结构相关的常量；σ(t)为材料当前应力；N为蠕变应力指数。该蠕变本构模型中的未知参数A和N可以通过应力松弛试验确定。蠕变过程缓慢，可以根据静力状态下弹簧拉力计算簧丝轴截面上的当前应力σ(t)：

式中：σ(t)为弹簧轴截面当前应力；F(t)为试验所得当前弹簧拉力；d为弹簧簧丝直径；C为弹簧旋绕比。

在确定弹簧的蠕变本构模型参数后，根据胡克定理得

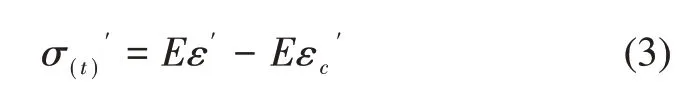
式中：σ(t)′为应力对时间的变化率：E为弹性模量；ε′为总应变对时间的变化率；εc′为蠕应变对于时间的变化率。应力松弛过程中，弹簧保持总应变不变，构件内应力随时间的推移而下降，因此，Eε′=0。将式(1)代入式(3)得

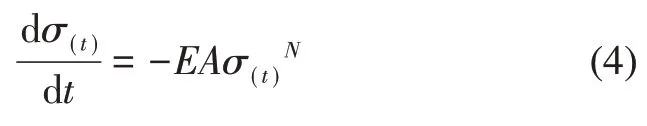
进一步对式(4)进行积分可以得到弹簧内应力与时间的关系表达式：

关于蠕变过程的应变数据与应力松弛过程的应力数据的转换已经得到充分研究，闫五柱等[17]提出通过应力松弛试验获得材料的蠕变参数，该方法中应力松弛比定义如下：

式中：σ(t0)为初始应力。弹簧当前蠕变量与当前应力之间的关系可以表示为

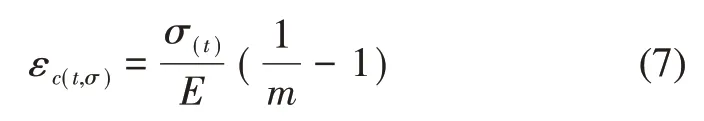
式中：εc(t,σ)为弹簧当前蠕变变形量。

3.2 应力松弛试验

ZN12 型高压断路器弹簧操动机构结构紧凑，分合闸弹簧安装空间狭小，难以直接在断路器上开展相关实验。因此，本文将分合闸弹簧从高压断路器本体拆离，然后进行应力松弛试验。搭建的试验台如图6所示。考虑到该型高压断路器分合闸弹簧长期处于静置的储能状态，本文设计的试验台将分合闸弹簧拉长至实际工况下的伸长位移后保持弹簧的伸长量不变，研究该型高压断路器分合闸弹簧在实际工况位移载荷作用下的应力松弛规律。本文设计的试验台在待测弹簧上布置了多个拉力传感器用于检测弹簧拉力，弹簧移动端是一套丝杆螺母机构，整个移动端组件通过联轴器与减速器连接。减速器侧输入轴转动，通过丝杆螺母机构传动将弹簧拉长实现加载，同时可以微调单根弹簧的拉伸长度，保证多根试验弹簧所受的拉力一致。该试验台可以同时对多根弹簧进行应力松弛试验，且在试验过程中不需要重复取下试验弹簧进行测量，避免弹簧重复装夹与加载产生较大试验误差。

试验台信号采集系统包括高精度拉压力传感器、电压信号放大器、多线路采集板卡和功能主机等。力传感器实时检测弹簧拉力的变化，并将各组弹簧力的变化转换成可测量的电压信号，通过放大器将传感器检测到的信号放大后，采集板卡对多路信号进行采样并将信号传输至功能主机中进行分析处理。

图6 弹簧应力松弛试验台Fig.6 Spring stress relaxation experiment

3.3 试验结果分析

该信号采集系统每间隔1 h 自动采集左端拉力传感器测得的弹簧载荷数据，将1 d所取得的24个拉力数据取平均值作为该弹簧当天应力松弛后的拉力，获得ZN12高压断路器分合闸弹簧在实际工况位移载荷作用下的1月的拉力结果如图7所示。

从应力松弛试验结果可知：虽然弹簧伸长量保持不变，在应力松弛作用下分合闸弹簧拉力均呈现缓慢减小趋势，且在初期下降速率比后期要快，变化规律符合应力松弛的阶段性特征[9]。将应力松弛试验过程中采集到的拉力结果代入式(2)得到弹簧的当前应力，进一步通过式(6)和(7)得到弹簧的应力和蠕变量，将蠕变量对时间求导得到短期蠕变速率与当前应力曲线并绘制在双对数坐标中。由式(1)可知：双对数坐标下的线性拟合斜率即为材料的蠕变应力指数N，所得截距表示常数A。根据计算结果，合闸弹簧材料的常数A为1.65×10-20，应力指数N为3.1，分闸弹簧材料的常数A为2.45×10-20，应力指数N为3.1。根据式(5)计算得到分合闸弹簧服役12，24和48月后应力松弛量，如表2所示。

图7 分合闸弹簧短期应力松弛结果Fig.7 Results of short-term stress relaxation of switching springs

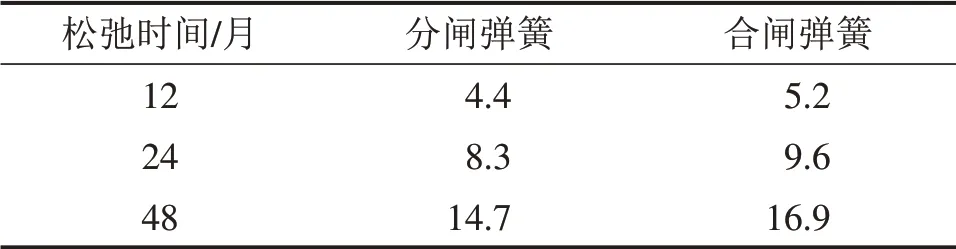
表2 弹簧后期应力松弛结果Table 2 Later stress relaxation result of spring %

4 分合闸弹簧应力松弛对操动机构运动特性影响

将分合闸弹簧未发生应力松弛时以及表2中12，24 和48月的应力松弛结果加载至所建立的高压断路器分合闸仿真模型上，利用ADAMS软件输出操动机构动触头的时间-位移曲线，研究分合闸弹簧应力松弛对断路器分合闸运动的影响结果如图8所示。

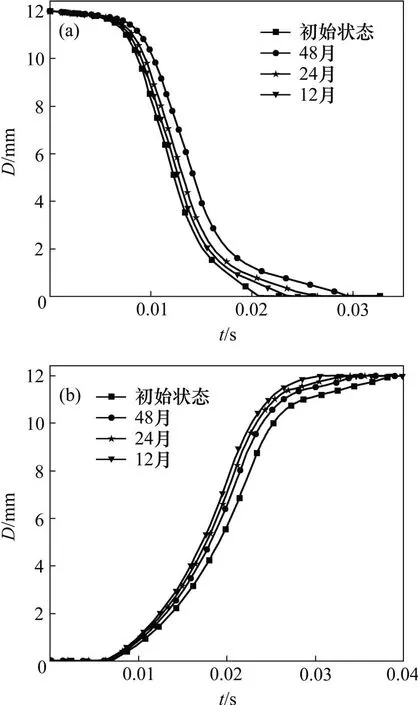
图8 不同应力松弛量下动触头位移特性Fig.8 Dynamic contact displacement characteristics under different stress relaxations

由图8可知：合闸弹簧应力松弛前后，高压断路器分合闸过程中的动触头最终位移均为12 mm，这一现象说明应力松弛对断路器分合闸过程中动触头的最终行程影响较小，但弹簧应力松弛以后的高压断路器分合闸完成时间将出现明显延迟。初始状态的分闸完成时间为21 ms，在应力松弛12，24 和48月后，分闸完成时间依次为23.4，25.7 和30.1 ms，呈现逐步递增的趋势。对于合闸运动，在应力松弛12，24 和48月后，合闸完成时间依次为24.8，26.4和30.8 ms。

以上研究表明：分合闸弹簧应力松弛对断路器动触头的行程影响较小，但会使机构的运动产生延时效应。延时虽然只有几毫秒，但考虑到断路器分合闸动作过程是瞬时动作，本身动作时间很短，其可靠的分合闸动作对时间要求严格。不同应力松弛量所导致的合闸延迟占总合闸时间的比例依次为5.5%，12.3%和26.8%，分闸延迟占总分闸时间的比例依次为11.4%，22.3%和42.4%。由仿真结果可知：应力松弛对分闸过程的影响比合闸的大，这是因为在合闸运动过程中，分闸弹簧被拉长，储存部分合闸弹簧的弹性势能阻碍合闸过程。弹簧应力松弛以后，分闸弹簧消耗的合闸操动功减少；相比于未发生应力松弛的情况，合闸完成时间将缩短，抵消了部分合闸弹簧应力松弛产生的延时效应。总体而言，应力松弛导致延时效应会影响断路器的正常分合闸运动，给线路的可靠运行带来不利影响。

5 结论

1)介绍了ZN12型高压断路器的结构特点，建立了该断路器的动力学仿真模型，并通过分合闸试验验证了仿真模型的准确性。

2) 通过弹簧短期应力松弛试验研究，得到该断路器分合闸弹簧在实际位移载荷工况下的Norton 蠕变本构模型中未知参数，进一步对所得蠕变本构模型进行求解分析，得到了分合闸弹簧后期的应力松弛情况。

3) 利用所建立的断路器仿真模型和应力松弛求解结果，得到不同应力松弛量对分合闸运动的影响。分合闸弹簧应力松弛对断路器操动机构的分合闸动作产生延时效应，且应力松弛对分闸过程影响更大。所导致的延时占总动作时间比例大，给高压断路器的分合闸动作带来不利影响。