基于相似日和分位数回归森林的光伏发电功率概率密度预测

何 锋，章义军，章建华，丁海华

基于相似日和分位数回归森林的光伏发电功率概率密度预测

何 锋，章义军，章建华，丁海华

（国网浙江安吉县供电有限公司，浙江 湖州 313300）

为提高光伏发电功率预测精度及可靠性，提出一种基于相似日和分位数回归森林（QRF）的光伏发电功率概率密度预测模型。选取某光伏电站实测数据为研究对象，在将光伏发电功率原始数据按不同天气类型进行分类的基础上，通过温度和风速2个特征向量选取相似日，并对相似日历史数据建立BP神经网络（BPNN）、支持向量机（SVM）和QRF预测模型。结果表明：晴天时，不同模型预测值均能较好跟踪真实值变化趋势，在13:00—16:00光伏发电功率下降时间段，QRF模型更接近真实值；多云或阴天时，在9:00—12:00，3种模型预测误差均较大；雨天时，在14:00—16:00光伏发电功率突变时间段，BPNN模型预测误差最大，SVM预测值相对于QRF模型更接近真实值，而在10:00—12:00，SVM模型预测误差增大。对不同模型不同天气类型下的预测误差，QRF模型预测性能更佳。

光伏发电功率；概率密度预测；相似日；分位数回归森林；核密度估计

受太阳辐射强度、风速、温湿度等气象因素的影响，光伏发电具有显著的波动性与随机性，大规模光伏系统并网将严重威胁电力系统稳定运行[1-2]。准确把握光伏发电功率变化特征并进行精确预测能够为电力系统调度、自动发电控制提供科学决策信息，从而有效降低光伏发电对电网造成的不利影响，提高资源利用率[3]。

目前，光伏发电功率预测按原理不同分为物理方法和统计预测方法。物理方法根据光伏电站地理位置、气象和太阳辐射等信息，通过太阳辐射传递方程、光伏组件运行方程进行预测[4]。统计预测方法将太阳辐射强度、风速、温湿度、气压等因素作为输入变量，通过线性回归、BP神经网络（back propagation neural network，BPNN）、支持向量机（support vector machines，SVM）等技术挖掘输入变量与光伏发电功率间的隐含关系，并结合天气预报数据进行预测[5-7]。文献[8]在分析光伏发电特性和季节特性的基础上，采用K均值算法对训练样本集进行聚类处理，并根据聚类结果分别建立SVM预测模型。文献[9]考虑季节类型、天气类型和气象因素对光伏发电功率的影响，选取相似日，建立最小二乘支持向量机预测模型。为进一步提高预测精度，相关学者提出了组合预测思路。文献[10-11]充分发挥不同预测模型优势，并按权重将各模型预测结果进行整合。文献[12-14]采用信号分解算法对光伏发电功率原始数据进行解耦，将其分解成若干特征互异的模态分量，然后对各分量建立预测模型，取得了较好预测结果。

上述模型主要集中于确定性的点预测，难以完全描述光伏发电功率波动范围及不确定性。为此，相关学者提出了光伏发电功率概率预测方法，如分位数回归、区间预测、密度预测等[15-17]。概率预测能够更好地描述光伏发电功率未来变化趋势、波动范围、不确定性及面临的风险，因此更有研究价值。

分位数回归森林（quantile regression forests，QRF）融合分位数回归和随机森林（random forest，RF）2种算法，能够获取不同分位点回归预测结果。作为一种非参数集成机器学习算法，QRF延续了RF算法运算速度快、模型性能受参数影响小、容噪性强等优点。因此，本文建立QRF预测模型，并采用核密度估计算法获得任意时刻光伏发电功率概率密度预测结果。

太阳辐射强度与太阳入射角、日照时长、光照强弱等因素密切相关，而太阳入射角等变量随季节更替周期性地变化也导致太阳辐射强度具有季节性、周期性的特点，这使得光伏发电功率在不同季节表现出较大差异。同一季节类型时，晴天、多云及雨天不同的天气状况也使得太阳辐射强度差异明显，导致光伏发电功率具有不同变化特征。因此，在建立预测模型前，有必要将光伏发电功率原始数据按季节类型、天气类型进行分类处理。此外，依据气象数据选取有效的相似日能更好利用历史数据进行预测，从而提高预测精度。

综上，本文建立基于相似日和QRF的光伏发电功率概率密度预测模型。首先，将光伏发电功率原始数据按天气类型进行分类，并通过温度、风速组成的特征向量选取相似日。其次，对相似日历史数据建立QRF预测模型并获得不同分位点回归预测值。最后，采用核密度估计算法获得任意时刻光伏发电功率概率密度预测结果。

1 相似日选取

1.2 光伏发电功率特性

光伏发电输出功率可按式(1)进行计算[18]：

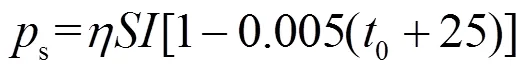
式中：为光伏电池转换效率，%；为光伏阵列面积，m2；为太阳辐射强度，kW/m2；0为工作环境温度，℃。

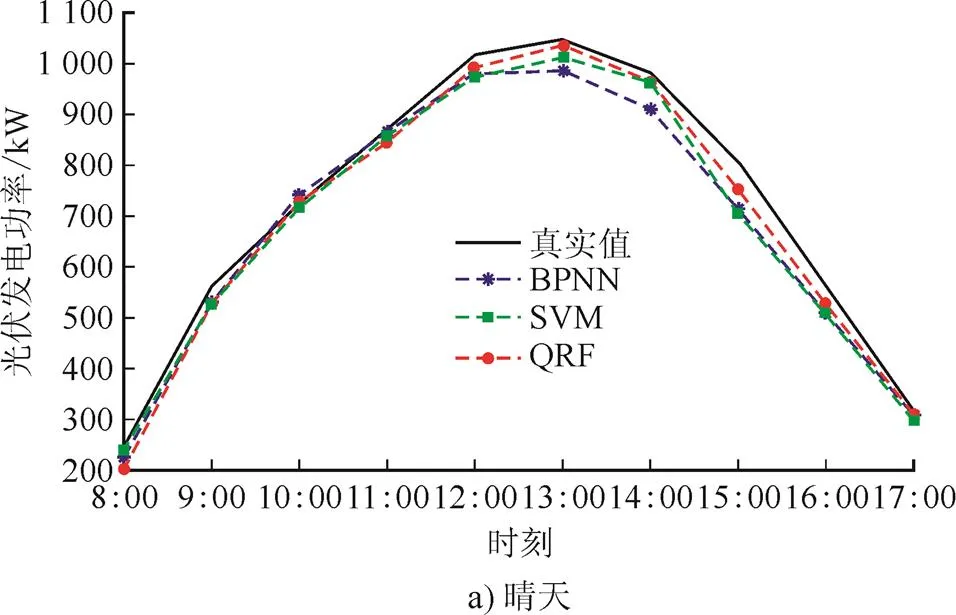
光伏电池转换效率和光伏阵列面积在光伏发电系统短时间运行期间基本保持不变，因此太阳辐射强度和温度是影响光伏发电功率的主要因素。然而，受晴天、多云及雨天等不同天气类型变化的影响，太阳辐射强度和环境温度表现出不同变化特征，导致光伏发电功率曲线差异较大。图1为不同天气类型时光伏发电功率变化曲线。

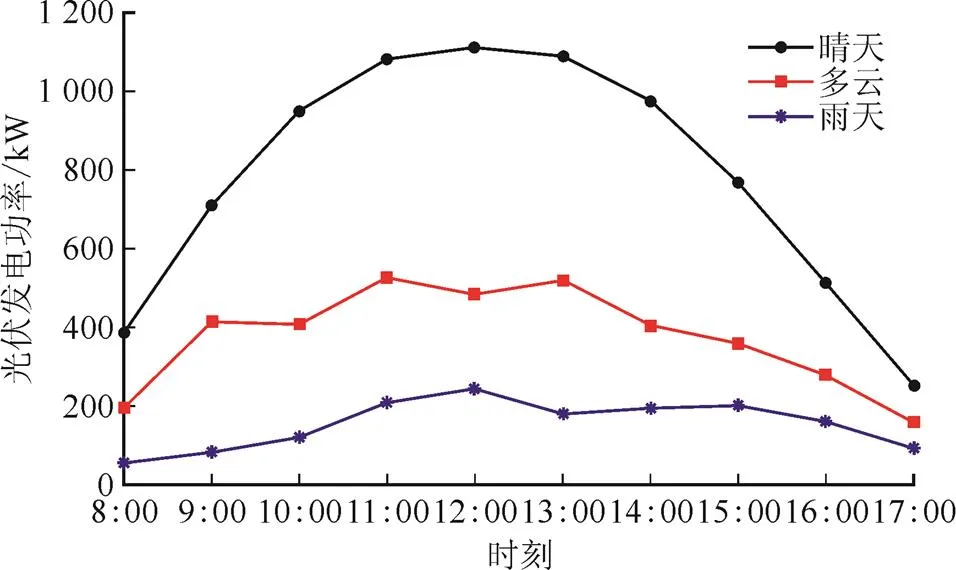
图1 不同天气类型光伏发电功率曲线

由图1可以看出：晴天时云量较少且温度较高，使得光伏发电功率维持在较高水平，光伏发电功率随着太阳辐射强度的变化表现出先上升后下降的变化趋势，并在12:00达到峰值，规律性较强；多云或阴天时辐射强度相对减弱，功率曲线波动较大；雨天时，光伏发电功率显著降低，曲线无明显的规律。因此，建立预测模型前，有必要按天气类型对光伏发电功率原始数据进行分类处理，以便更好地利用相似日历史数据，从而有效提高预测精度。

1.2 相似日特征向量

在将光伏发电功率原始数据按晴天、多云、雨天不同天气类型进行分类的基础上，本文利用相似日原理选取与待预测日气象特征相近的历史日。光伏发电功率受太阳辐射强度和温度的影响，理论上选取相似日的特征向量应为太阳辐射强度和温度。由于太阳辐射强度与季节类型、天气类型和云量等因素相关，在进行原始数据分类时已经考虑季节类型和天气类型的影响，因此在构建相似日特征向量时主要考虑云量对太阳辐射强度的影响。然而，云量预测较难实现，因此本文选取风速作为太阳辐射强度的影响因素。最终，本文选取相似日的特征向量为温度和风速2个变量。

光伏发电有效输出集中于白天太阳辐射较强的时间段，选取每天08:00—17:00时间段内的10个整点时刻作为基准点并进行预测。由前述分析可得，待预测日气象特征向量0可表示为

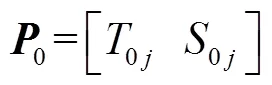
式中0j、0j分别为待预测日基准点的温度和风速。

历史第日气象特征向量可表示为

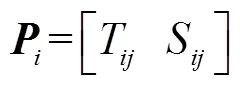
式中T、S分别为历史第日基准点温度和风速。

1.3 相似度计算

本文采用灰色关联分析法度量历史日气象特征向量与待预测日气象特征向量间的相似程度，从而选取有效相似日。0与两向量间相关性记为关联度r，其计算公式为[19]

式中：为气象特征向量维数，本文取=20；ε()为待预测日和第个历史日第个气象特征分量的关联系数，按式(5)进行计算。

式中：'()、x'()分别为归一化后的待预测日和第个历史日第个气象特征分量；为分辨系数，本文取=0.5。

r越接近于1，则说明该日与待预测日气象特征更相近，光伏发电功率变化特征与规律也越相似；r接近于0，则说明该日与待预测日气象特征差异较大，不能选作相似日。

2 基于QRF的概率密度预测

2.1 分位数回归森林基本原理

QRF融合分位数回归和RF算法，可看作是适应性近邻分类与回归过程。对任意=，可以得到原始个观察值一个权重集合w()，=1,2,3。QRF将所有因变量观测值的加权和作为因变量条件均值(|=)的估计[20]。

QRF定义(1{Y≤}|=)的估计为观测值1{Y≤}的加权平均，即

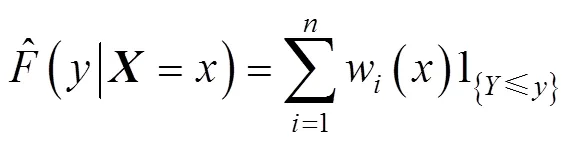
QRF算法具体步骤为：1）生成棵决策树(θ)，=1,2,…1。对每棵决策树每个叶节点，考察该叶节点所有观测值；2）给定=，遍历所有决策树。计算每棵决策树观测值的权重w(,θ)，∈{1,2,…,}。通过对决策树权重w(,θ)，=1,2,…,取平均得到每个观测值∈{1,2,…,}的权重w()；3）对所有∈，利用步骤2)得出的权重，通过式(6)计算分布函数的估计。

2.2 核密度估计

QRF模型可以获得不同分位点条件下的光伏发电功率预测值，进而采用核密度估计获得任意时刻光伏发电功率概率密度预测结果。

核密度估计通过同一未知分布函数的随机变量来估计其密度函数。设1,2, …,X是取自一元连续总体的样本，在任意点处的总体密度函数()的核密度估计定义为[21]

3 算例分析

选取某光伏电站实测数据为研究对象，在将光伏发电功率原始数据按晴天、多云和雨天等不同天气类型进行分类的基础上，通过温度和风速2个特征向量选取相似日，并对相似日历史数据建立BPNN、SVM和QRF预测模型，以实现光伏发电功率提前1 h的超短期预测。图2为BPNN、SVM和QRF对该光伏电站晴天、多云和雨天提前1 h的预测结果。其中：BPNN学习率设置为0.001，学习目标为0.01，迭代5 000次；SVM模型的惩罚因子和核参数2个变量通过网格搜索选取，参数范围设置为[−8,8]，迭代步长为1；QRF模型取0.5分位点条件下的预测值，决策树数目设置为1 000，节点最小尺寸为10，每棵决策树从输入变量集合中随机选取try=/3个变量进行权重学习，为输入变量数目。为获得条件分布，设置分位点范围为0.01~0.99，步长为0.01，对每个预测点即可获得99个预测结果。

由图2a)可见：晴天时光伏发电功率变化平缓，具有较强的规律性；不同模型预测值均能较好跟踪真实值变化趋势，具有较好预测结果；在13:00—16:00光伏发电功率下降时间段，QRF模型更接近真实值，有效降低了预测误差。

多云或阴天时，由于云的遮挡，光伏阵列单位面积太阳辐射强度降低，使得光伏发电功率降低的同时具有较强的波动性与随机性。由图2b)可见，9:00—12:00时间段，3种模型均有较大预测误差。

由图2c)可见：雨天光伏发电功率相对于晴天和多云天气显著降低，且其变化曲线规律性较差，增大了预测难度；在14:00—16:00光伏发电功率突变时间段，BPNN模型预测误差最大；SVM相对于QRF模型，其预测值更接近真实值；在10:00—12:00时间段，由于气象因素的突变导致输出功率降低，此时SVM模型预测值无法正确反映功率变化趋势，导致预测误差增大。

为定量评价不同模型预测性能，采用平均绝对百分比误差（mean absolute percentage error，MAPE）和均方根误差（root mean square error，RMSE）2种评价指标统计预测误差，计算公式分别为：

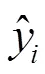
表1为不同模型、不同天气类型下光伏发电功率预测误差。可以看出，QRF模型预测性能更佳。

表1 不同模型预测误差统计

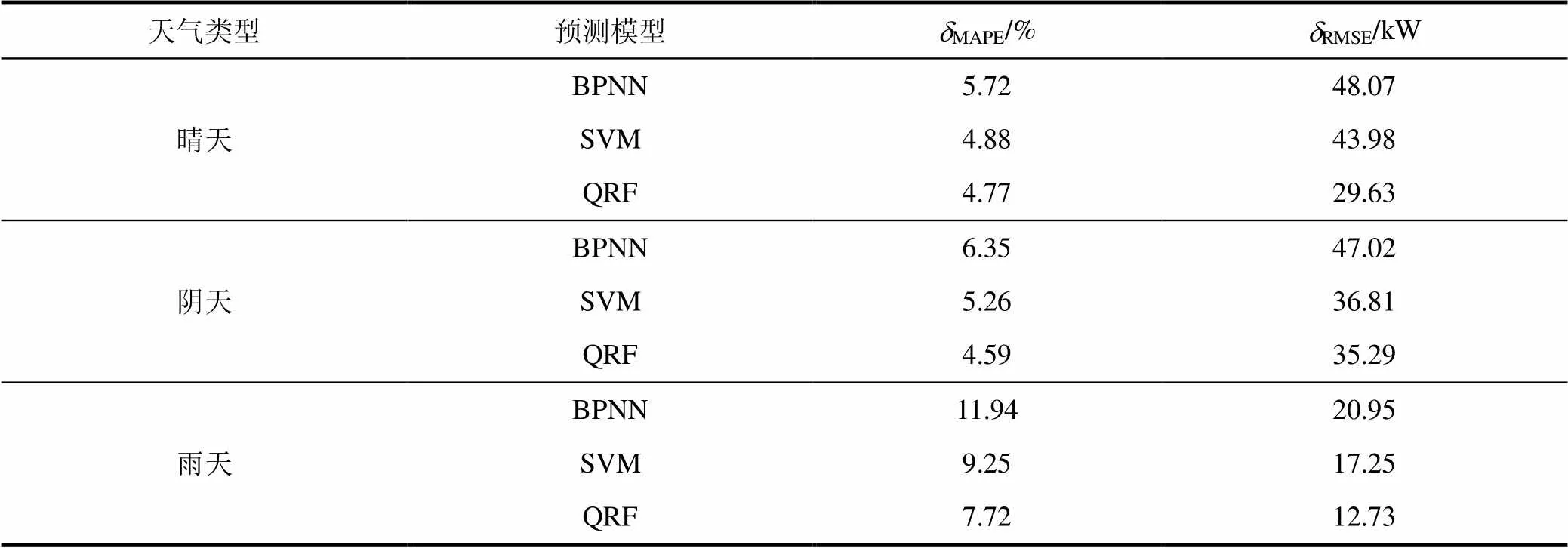
Tab.1 Statistics of the forecasting errors of different models

对每个基准点，QRF模型能够得到99个分位点条件下的预测结果，进而采用核密度估计算法获得任意时刻光伏发电功率概率密度预测值。图3为雨天时不同分位点光伏发电功率预测结果。由图3可见，在11:00—13:00时间段内，QRF光伏发电功率预测模型预测值波动范围更大，这也间接反映此时间段内光伏发电功率真实值波动性与随机性较强，其变化特征与规律较难把握。

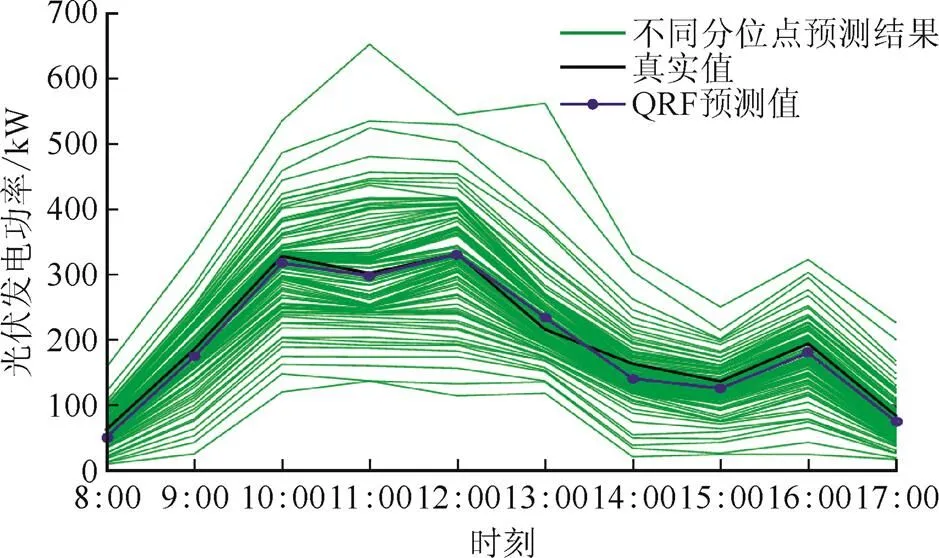
图3 不同分位点光伏发电功率预测曲线（雨天）

图4为雨天时不同时刻光伏发电功率概率密度预测结果。雨天光伏发电功率具有较强的波动性与随机性，而概率密度预测结果能够更好地描述光伏发电功率波动范围及不确定性，从而更有利于指导电力调度部门做出科学合理的决策。由图4可见，不同时刻光伏发电功率真实值与预测值均出现在概率密度曲线峰值附近，说明预测值以较大概率接近真实值，验证了QRF预测模型有效性。

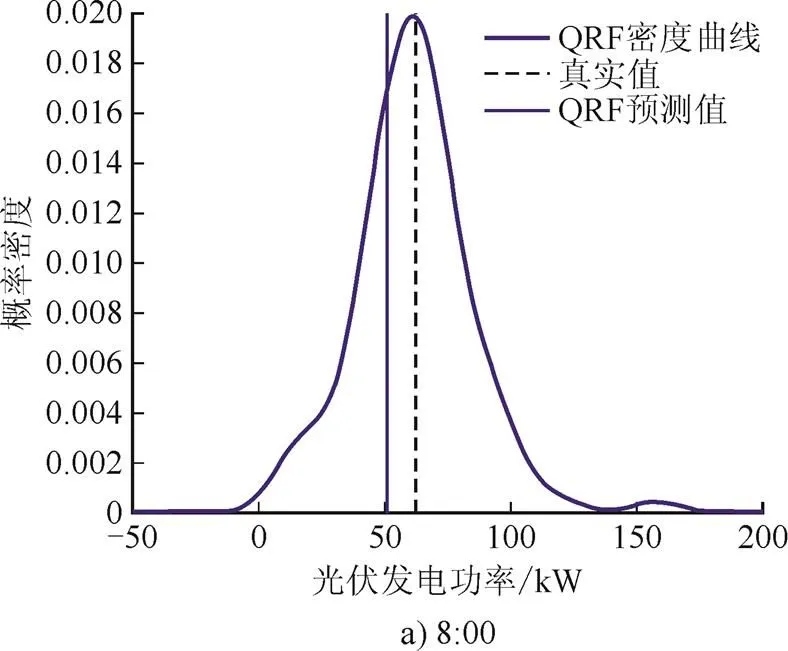
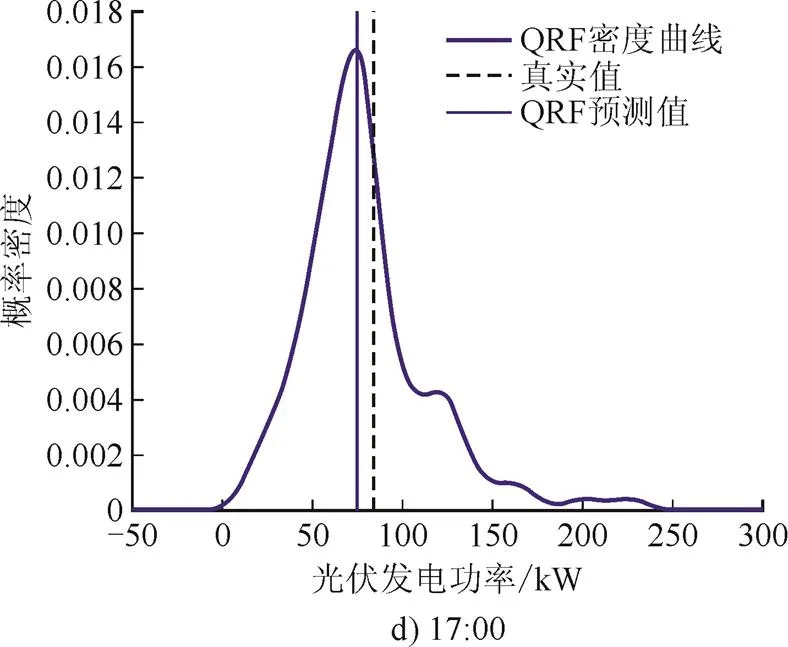
图4 不同时刻光伏发电功率概率密度预测（雨天）

4 结 语

本文在对光伏发电功率原始数据按天气类型进行分类的基础上，确定温度和风速为特征向量并采用灰色关联度分析法选取相似日；建立了光伏发电功率分位数回归森林预测模型，进而采用核密度估计算法获得任意时刻概率密度预测结果，通过实际算例验证了模型有效性。

［1］ PIERRO M, BUCCI F, DE FELICE M, et al. Multi-model ensemble for day ahead prediction of photovoltaic power generation[J]. Solar Energy, 2016, 134: 132-146.

［2］ 刘琳. 光伏电站有功功率优化分配[J]. 热力发电, 2015, 44(11): 104-108. LIU Lin. Active power control in photovoltaic power plants[J]. Thermal Power Generation, 2015, 44(11): 104-108.

［3］ 成珂, 郭黎明, 王亚昆. 聚类分析在光伏发电量预测中的应用研究[J]. 可再生能源, 2017, 35(5): 68-73. CHENG Ke, GUO Liming, WANG Yakun. Application of cluster analysis in forecasting photovoltaic power generation[J]. Renewable Energy Resources, 2017, 35(5): 68-73.

［4］ 张玉, 黄睿, 张振涛, 等. 基于克里格模型的光伏发电量预测[J]. 热力发电, 2017, 46(4): 27-32. ZHANG Yu, HUANG Rui, ZHANG Zhentao, et al. Photovoltaic power generation prediction based on Krige model[J]. Thermal Power Generation, 2017, 46(4): 27-32.

［5］ GUO H P, WU S H, WANG Z Q, et al. Linear regression for forecasting photovoltaic power generation[J]. Applied Mechanics & Materials, 2014, 494: 1771-1774.

［6］ 李芬, 宋启军, 蔡涛, 等. 基于PCA-BPNN的并网光伏电站发电量预测模型研究[J]. 可再生能源, 2017, 35(5): 61-67. LI Fen, SONG Qijun, CAI Tao, et al. Based on principal component analysis and the BP neural network in the application of grid-connected photovoltaic power energy prediction[J]. Renewable Energy Resources, 2017, 35(5): 61-67.

［7］ 张玉, 莫寒, 张烈平. 基于模糊支持向量机的光伏发电量预测[J]. 热力发电, 2017, 46(1): 116-120. ZHANG Yu, MO Han, ZHANG Lieping. Photovoltaic power prediction based on fuzzy support vector machine[J]. Thermal Power Generation, 2017, 46(1): 116-120.

［8］ 张雨金, 杨凌帆, 葛双冶, 等. 基于Kmeans-SVM的短期光伏发电功率预测[J]. 电力系统保护与控制, 2018, 46(21): 118-124. ZHANG Yujin, YANG Lingfan, GE Shuangye, et al. Short-term photovoltaic power forecasting based on Kmeans algorithm and support vector machine[J]. Power System Protection and Control, 2018, 46(21): 118-124.

［9］ 傅美平, 马红伟, 毛建容. 基于相似日和最小二乘支持向量机的光伏发电短期预测[J]. 电力系统保护与控制, 2012, 40(16): 65-69. FU Meiping, MA Hongwei, MAO Jianrong. Short-term photovoltaic power forecasting based on similar days and least square support vector machine[J]. Power System Protection and Control, 2012, 40(16): 65-69.

［10］ 单英浩, 付青, 耿炫, 等. 基于改进BP-SVM-ELM与粒子化SOM-LSF的微电网光伏发电组合预测方法[J]. 中国电机工程学报, 2016, 36(12): 3334-3342. SHAN Yinghao, FU Qing, GENG Xuan, et al. Combined forecasting of photovoltaic power generation in microgrid based on the improved BP-SVM-ELM and SOM-LSF with particlization[J]. Proceedings of the CSEE, 2016, 36(12): 3334-3342.

［11］ YANG X, JIE R, HONG Y. Photovoltaic power forecasting with a rough set combination method[C]// 2016 UKACC 11th International Conference on Control (CONTROL), Belfast, 2016: 1-6.

［12］ LI Q, SUN Y, YU Y, et al. Short-term photovoltaic power forecasting for photovoltaic power station based on EWT-KMPMR[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(20): 265-273.

［13］ 李多, 董海鹰, 杨立霞. 基于EMD与ELM的光伏电站短期功率预测[J]. 可再生能源, 2016, 34(2): 173-177. LI Duo, DONG Haiying, YANG Lixia. The short-term power forecasting of photovoltaic plant based on EMD-ELM[J]. Renewable Energy Resources, 2016, 34(2): 173-177.

［14］ 张立影, 刘智昱, 孟令甲, 等. 基于小波变换和神经网络的光伏功率预测[J]. 可再生能源, 2015, 33(2): 171-176. ZHANG Liying, LIU Zhiyu, MENG Lingjia, et al. Photovoltaic output power prediction approach based on wavelet transform and neural network[J]. Renewable Energy Resources, 2015, 33(2): 171-176.

［15］ 路志英, 任一墨, 葛路琨. 基于样条估计分位数回归的光伏功率回归模型[J]. 湖南大学学报(自然科学版), 2017, 44(10): 96-103. LU Zhiying, REN Yimo, GE Lukun. Photovoltaic power regression model based on spline estimation and quantile regression[J]. Journal of Hunan University (Natural Sciences), 2017, 44(10): 96-103.

［16］ 陈云龙, 殷豪, 孟安波, 等. 基于模糊信息粒化的光伏出力区间预测[J]. 电测与仪表, 2018, 55(14): 63-68. CHEN Yunlong, YIN Hao, MENG Anbo, et al. PV power interval prediction based on fuzzy information granulation[J]. Electrical Measurement & Instrumentation, 2018, 55(14): 63-68.

［17］ 程泽, 刘冲, 刘力. 基于相似时刻的光伏出力概率分布估计方法[J]. 电网技术, 2017, 41(2): 117-124. CHENG Ze, LIU Chong, LIU Li. A method of probabilistic distribution estimation of PV generation based on similar time of day[J]. Power System Technology, 2017, 41(2): 117-124.

［18］ 杨锡运, 刘欢, 张彬, 等. 组合权重相似日选取方法及光伏输出功率预测[J]. 电力自动化设备, 2014, 34(9): 118-122.YANG Xiyun, LIU Huan, ZHANG Bin, et al. Similar day selection based on combined weight and photovoltaic power output forecasting[J]. Electric Power Automation Equipment, 2014, 34(9): 118-122.

［19］ 李芬, 李春阳, 糜强, 等. 基于GRA-BPNN时变权重的光伏短期出力组合预测[J]. 可再生能源, 2018, 36(11): 1605-1611. LI Fen, LI Chunyang, MI Qiang, et al. The time-varying weight ensemble forecasting of short-term photovoltaic power based on GRA-BPNN[J]. Renewable Energy Resources, 2018, 36(11): 1605-1611.

［20］ NICOLAI M. Quantile regression forests[J]. Journal of Machine Learning Research, 2006, 7(2): 983-999.

［21］ TRAPERO J R . Calculation of solar irradiation prediction intervals combining volatility and kernel density estimates[J]. Energy, 2016, 114: 266-274.

Forecasting of photovoltaic power generation probability density based on similar day and quantile regression forests

HE Feng, ZHANG Yijun, ZHANG Jianhua, DING Haihua

(State Grid Zhejiang Anji County Power Supply Co., Ltd., Huzhou 313300, China)

In order to improve the forecasting accuracy and reliability of photovoltaic power generation, a photovoltaic power generation probability density forecasting model based on similar day and quantile regression forests (QRF) is proposed. The measured data of a photovoltaic power station are selected as the research object. On the basis of classifying the original data of the photovoltaic power generation according to different weather types, similar days are selected by two eigenvectors (temperature and wind speed). Moreover, the BP neural network (BPNN) model, support vector machine (SVM) model and QRF forecasting model are established for the historical data of similar days. The results show that, on sunny days, the forecasting results of different models can better track the change trend of true values, and the QRF model’s result is closer to the true value during the period of photovoltaic power reduction from 13:00 to 16:00. On cloudy days, the forecasting errors of the above three models are relatively large from 9:00 to 12:00. In rainy days, during the sudden change of photovoltaic power generation from 14:00 to 16:00, the BPNN model has the largest forecasting error, and the SVM model’s forecasting result is closer to the true value than the QRF model, but the forecasting error of the SVM model increases from 10:00 to 12:00. The QRF model has better prediction performance for different weather types among different models.

power of photovoltaic power generation, probability density forecasting, similar day, quantile regression forests, kernel density estimation

TM914

A

10.19666/j.rlfd.201902031

何锋, 章义军, 章建华, 等. 基于相似日和分位数回归森林的光伏发电功率概率密度预测[J]. 热力发电, 2019, 48(7): 64-69. HE Feng, ZHANG Yijun, ZHANG Jianhua, et al. Forecasting of photovoltaic power generation probability density based on similar day and quantile regression forests[J]. Thermal Power Generation, 2019, 48(7): 64-69.

2019-02-25

何锋(1987—)，男，工程师，主要研究方向为电气工程及其自动化，hefeng302@163.com。

（责任编辑 刘永强）