间接式超临界二氧化碳塔式太阳能热发电系统仿真优化

何欣欣，薛志恒，陈会勇，王伟锋

间接式超临界二氧化碳塔式太阳能热发电系统仿真优化

何欣欣，薛志恒，陈会勇，王伟锋

（西安热工研究院有限公司，陕西 西安 710054）

本文建立了间接式超临界二氧化碳塔式太阳能热发电系统数学模型，对该系统在不同的透平入口温度、主压缩机出口压力以及循环压比下进行仿真，分析了全厂热效率的变化规律。结果表明：随着透平入口温度的升高，全厂热效率出现先增大后减小的规律，在750 ℃附近存在最佳透平入口温度；随着循环压比的增大，全厂热效率出现先增大后减小的规律，对于不同的主压缩机出口压力和透平出口温度均存在最佳循环压比。最后提出了该系统的2种参数优化方案，并给出主压缩机入口压力20~35 MPa、透平入口温度500~850 ℃范围内的参数优化值。

超临界；二氧化碳；塔式；太阳能热发电；腔式吸热器；参数优化

近年来，太阳能热发电作为一种太阳能大功率集中利用的发电方式受到广泛研究及推广应用。许多国家建立了各种规模的以朗肯循环为动力循环的示范性光热电站[1]。动力循环的高参数化是提高太阳能热发电效率的重要途径之一，以超临界二氧化碳为工质的布雷顿循环在透平入口温度为500~800 ℃时，与同等运行参数下的朗肯循环相比，具有效率高、结构紧凑等特征和优势，与太阳能热发电的运行特性相匹配[2-3]。因此，将布雷顿循环与太阳能热发电相结合可以进一步提升太阳能热发电系统的效率。

Iverson等人[4]的实验研究表明：将透平入口工质温度提高至600 ℃以上对超临界二氧化碳布雷顿光热发电的全厂热效率提高有显著作用。Milani等人[5]比较了直接式和间接式2种不同的吸热方式在光热发电系统中的特性及其适用性。何雅玲等[6]对采用直接式吸热的超临界二氧化碳塔式光热发电系统进行研究并得出光热电站的全厂热效率随循环参数的变化规律。

目前，国内外的研究主要侧重超临界二氧化碳塔式光热发电系统的热力学分析以及动力循环结构的比较和优化，并得出规律性定性结论，较少涉及系统的定量优化，尤其对采用间接式吸热的塔式光热发电系统的定量优化。

本文首先建立了采用间接式吸热的超临界二氧化碳塔式热发电系统的仿真模型，然后研究了动力循环中透平入口温度、主压缩机出口压力以及循环压比3个重要运行参数对全厂热效率的影响，给出了2种针对该系统的优化设计方案及其参数优化结果。

1 热力学模型

间接式超临界二氧化碳塔式太阳能热发电系统由4个部分组成，分别为定日镜场子系统、腔式吸热器子系统、中间换热器子系统和超临界二氧化碳动力循环子系统。对动力循环子系统而言，本文以典型再压缩循环为例进行分析，在此基础上可以衍生出多种循环结构[7]。间接式超临界二氧化碳塔式太阳能热发电系统仿真模型如图1所示。

图1 间接式超临界二氧化碳塔式太阳能热发电系统模型

本文研究该系统在某一时刻的稳态运行过程，不考虑系统随季节或一天时间的变化关系，且研究侧重吸热器子系统和动力循环子系统参数和性能的变化。对该间接式超临界二氧化碳塔式太阳能热发电系统热力学模型作如下假设：

1）单一时刻的太阳辐射为定值；

2）系统在稳定状态下运行；

3）各个设备的压损、散热损失、机械损失、电气损失等可忽略。

1.1 定日镜场子系统

定日镜场子系统存在关系：

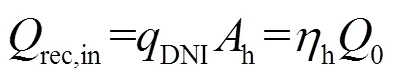
式中，rec,in为吸热器表面吸收的能量，DNI和0分别为入射至定日镜场的法向辐射强度和辐射能量，h和h分别为定日镜场的面积和总体效率。参考前人对稳态运行系统的处理方法，假设定日镜场子系统的总体效率为定值[6,8]。

1.2 腔式吸热器子系统

与直接式太阳能热发电吸热系统中常用的圆柱形吸热器不同，间接式吸热系统中一般采用以熔融盐作为传热介质的腔式吸热器，熔融盐从定日镜场子系统吸收热量并通过中间换热器传递给动力循环子系统。间接式吸热系统凭借熔融盐蒸气气压低、比热容高等特点，与直接式吸热系统相比，在同样的结构参数下可以获得更大的辐射通量，并且可以直接兼容外置的熔融盐储能装置[9]，将新能源的利用与储存较好地结合在一起，因而在电网深度调峰时具有一定的优势。

熔融盐的工作温度存在一个范围，超过最高工作温度时熔融盐可能会发生分解或者反应，低于最低工作温度时熔融盐可能会产生析出或者结晶等现象。在超临界二氧化碳动力循环中，透平入口的最佳工作温度为500~850 ℃，而朗肯循环光热电站普遍使用质量分数分别为60%的NaNO3和40%的KNO3混合而成的熔融盐，该熔融盐在600 ℃左右会发生分解，对于透平入口温度超过600 ℃时已不再适用。

本文间接式吸热系统熔融盐的最高和最低工作温度需满足图1中动力循环子系统的状态点5（透平入口温度）以及状态点4（高温回热器至中间换热器温度）。通过综合比较多种熔融盐的传热性能和适用范围，选择LiCl-KCl（质量分数分别为45%和55%）混合盐作为本文间接式吸热器的工质，该熔融盐工作温度范围为355~1 100 ℃[10]，满足动力循环子系统的要求，LiCl-KCl混合盐的物性参数参考文献[10]。

对于腔式吸热器而言，存在如下关系：

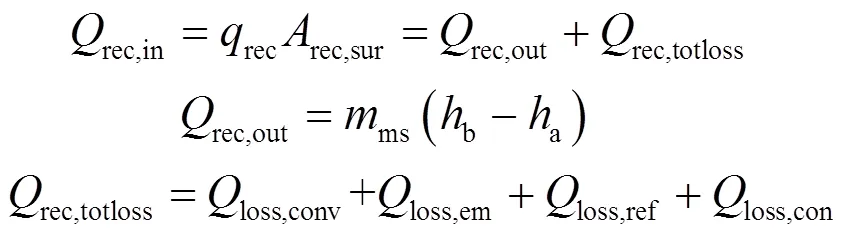
式中，rec和rec分别为吸热器表面的热流密度和表面积，rec,out和ms分别为熔融盐吸收的热量和质量流量，a和b分别为通过吸热器进出口a、b熔融盐的焓值，rec,totloss为熔融盐吸收的热量，loss,conv、loss,em、loss,ref和loss,con分别为吸热器的对流、辐射、反射和导热损失。

辐射损失在系统热损失中占比较大且随着温度升高占比会增大，计算公式为

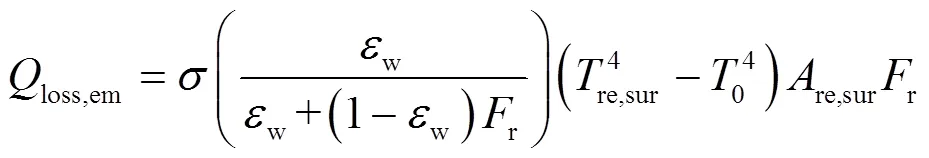
式中，为斯忒藩-玻尔兹曼常数，re,sur为吸热器的表面温度，w为表面辐射率，r为视角系数，0为环境温度。

对流损失包含强制对流和自然对流2种，计算公式为

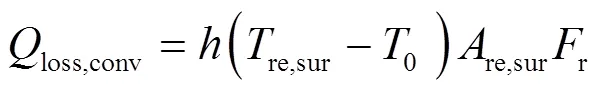
式中，为自然或强制对流换热系数，根据努塞尔数计算，具体计算方法参见文献[11]。

反射损失的计算公式为

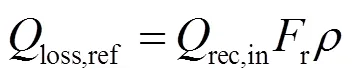
式中为吸热器的表面反射率。

导热损失所占比例对于保温效果良好的吸热器一般可以忽略。吸热器子系统具体的能量关系参考文献[11]，最终的热力学平衡状态采用迭代方法进行计算，吸热器热效率rec的定义为熔融盐吸收的热量rec,out与吸热器表面吸收的能量rec,in之比

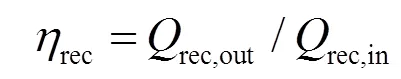
1.3 中间换热器子系统

中间换热器子系统的作用是连接吸热器子系统和动力循环子系统，利用熔融盐将吸热器子系统所吸收的热量传递给动力循环子系统中的二氧化碳工质。由于假设各个组件的散热损失忽略不计，因此该换热器中存在关系

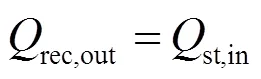
式中st,in为动力循环子系统中二氧化碳吸收的 热量。

中间换热器子系统的熔融盐出口温度b通过动力循环中透平入口温度5和中间换热器的热端端差Δ计算。

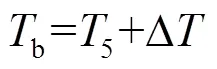
熔融盐入口温度a通过假设中间换热器两端的熵增保持不变计算[12]。

1.4 动力循环子系统

进入超临界二氧化碳动力循环的能量与二氧化碳工质的质量流量之间的关系为

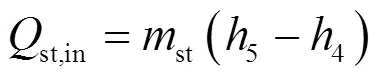
式中，st为二氧化碳的质量流量，5和4分别为二氧化碳的焓值。

采用回热器回热效能对超临界二氧化碳动力循环子系统进行热力学建模。高温回热器的回热效能为

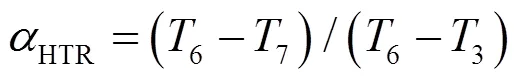
式中T为图1中各点处温度。

对于低温回热器而言，如果高压侧流体的比热容大于低压侧流体比热容，其回热效能采用式(11)计算，否则采用式(12)：

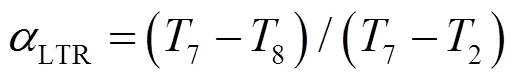
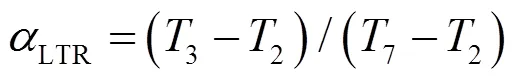
动力循环的热效率st定义为动力循环子系统的净输出功率与其工质吸收的热量之比

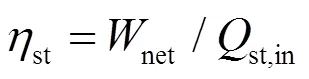
式中net为动力循环子系统的输出功率。动力循环子系统具体的能量关系参考文献[13]。

全厂的热效率verall的计算公式为

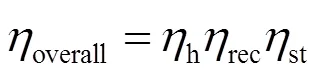
2 仿真结果及分析

基于MATLAB平台建立了50 MW间接式超临界二氧化碳塔式太阳能热发电系统的数学模型。该模型太阳能热发电系统设计参数见表1，二氧化碳的物性参数根据NIST提供的REFPROP 9.1程序包计算得出[14]。

透平入口温度5、主压缩机出口压力2以及循环压比c是超临界二氧化碳动力循环中的重要运行参数，共同影响动力循环子系统以及吸热器子系统的热效率，进而影响全厂的热效率。因此，本文针对该系统在不同的透平入口温度、主压缩机出口压力以及循环压比下进行仿真，分析全厂热效率随3个参数的变化规律，并根据该变化规律提出2种参数优化方案。

表1 太阳能热发电系统设计参数

Tab.1 Design parameters of the solar tower power plant

2.1 模型验证

选用文献[15]的参数对腔式吸热器进行仿真，文献[15]中使用的是水蒸气动力循环，对应的熔融盐为60%NaNO3-40%KNO3，吸热器参数及仿真结果见表2，其余参数与本文一致。由表2可见，2种模型的相对偏差为0.40%。

表2 熔融盐腔式吸热器参数及仿真结果

Tab.2 Parameters and simulation results of the molten salt cavity receiver

图2为500~850 ℃时超临界二氧化碳再压缩循环模型的仿真结果，并与NREL和Dostal等人的研究结果[16]进行对比。由图2可见，本文与NREL和Dostal等人的循环热效率曲线基本吻合，模型的最大相对误差为1.71%，平均相对误差为0.35%，证明本文超临界二氧化碳动力循环模型可靠有效。

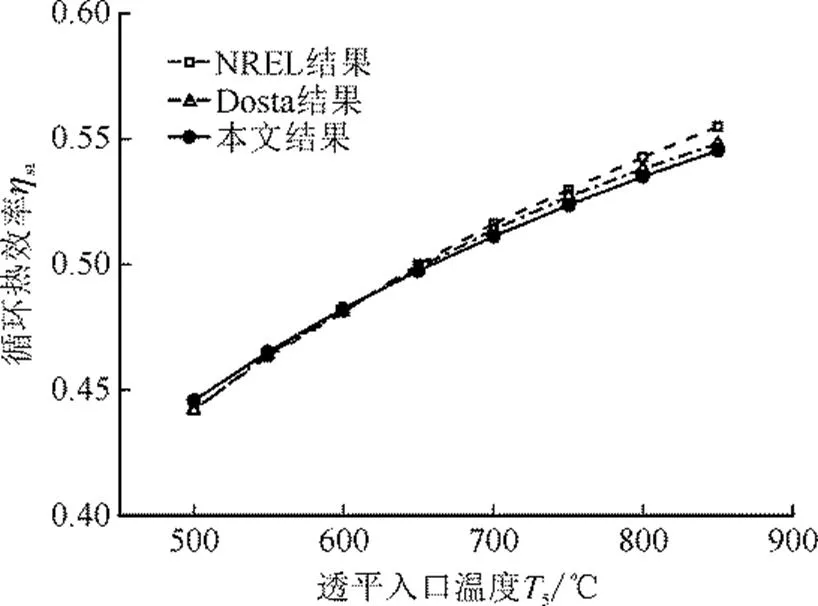
图2 超临界二氧化碳再压缩循环模型仿真结果

2.2 主压缩机出口压力和循环压比对热效率的影响

在典型的再压缩布雷顿循环中，循环压比c定义为主压缩机出口压力2和入口压力1的比

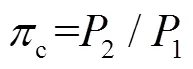
当透平入口温度一定（以T5=750 ℃为例）时，不同主压缩机出口压力下全厂热效率随循环压比的变化如图3所示。由图3可见：随着循环压比的增大，全厂的热效率随循环压比的变化趋势会出现一个最大值；对于不同的主压缩机出口压力，都存在相应的最佳循环压比，且随着主压缩机出口压力升高，最佳循环压比逐渐增大。此外，根据图3可知，主压缩机出口压力每提升5 MPa，最佳全厂热效率可以提升约0.5~1.0个百分点。

2.3 透平入口温度对热效率的影响

图4为不同主压缩机出口压力下全厂热效率随透平入口温度的变化。由图4可见，当主压缩机出口压力一定时，随透平入口温度的升高，全厂热效率出现先增大后减小的变化规律，在透平入口温度为750 ℃附近全厂热效率出现最大值，且随着主压缩机出口压力的升高，全场热效率最高时的透平入口温度增大。这与燃煤超临界二氧化碳动力循环中热效率随透平入口温度升高而增大的规律不同[17]。

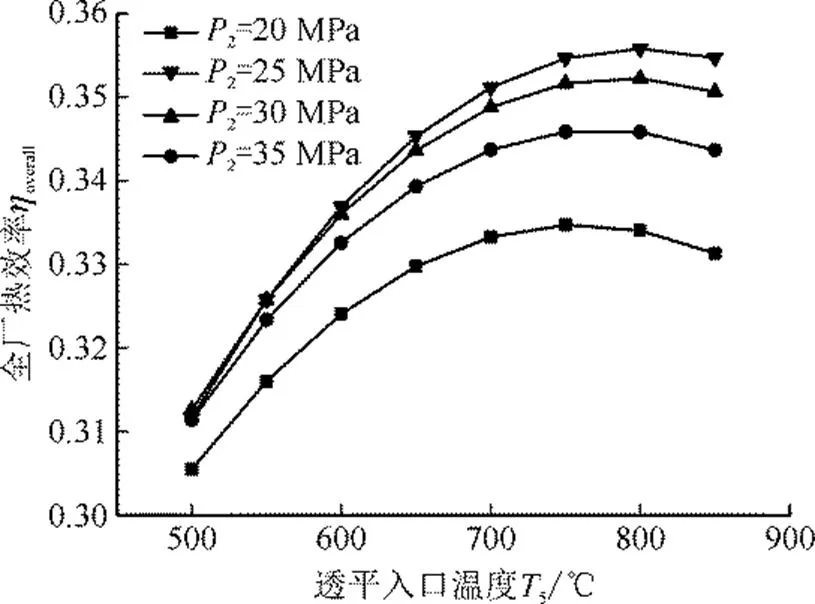
图4 不同主压缩机出口压力P2下全厂热效率随透平入口温度的变化

在太阳能热发电系统中，吸热器的表面温度会随着透平入口温度的升高而升高。图5为吸热器子系统能量损失随透平入口温度的变化。由图5可见，吸热器子系统的辐射损失和对流损失随透平入口温度的升高增大，反射损失逐渐减小，导热损失所占比例很小且基本不变。

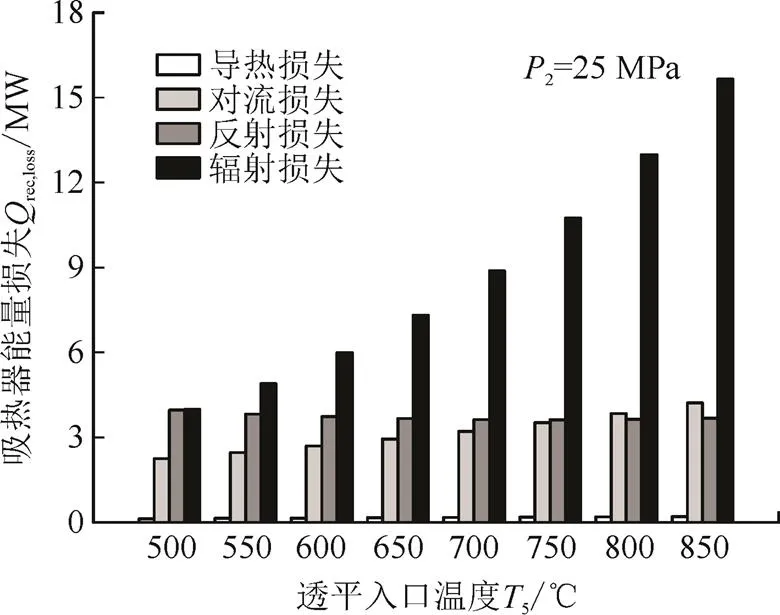
图5 吸热器子系统能量损失随透平入口温度的变化

根据式(3)，吸热器的辐射损失与吸热器表面温度呈四次方的关系，因此辐射损失会随着吸热器表面温度的升高而迅速增大，各个能量损失叠加的结果导致吸热器的热效率迅速减小。图6为热效率随透平入口温度的变化。由图6可见，动力循环子系统的循环热效率随透平入口温度升高而平稳增大。因此，当吸热器子系统热效率的下降速率大于动力循环子系统热效率的增大速率时，全厂热效率出现最大值。

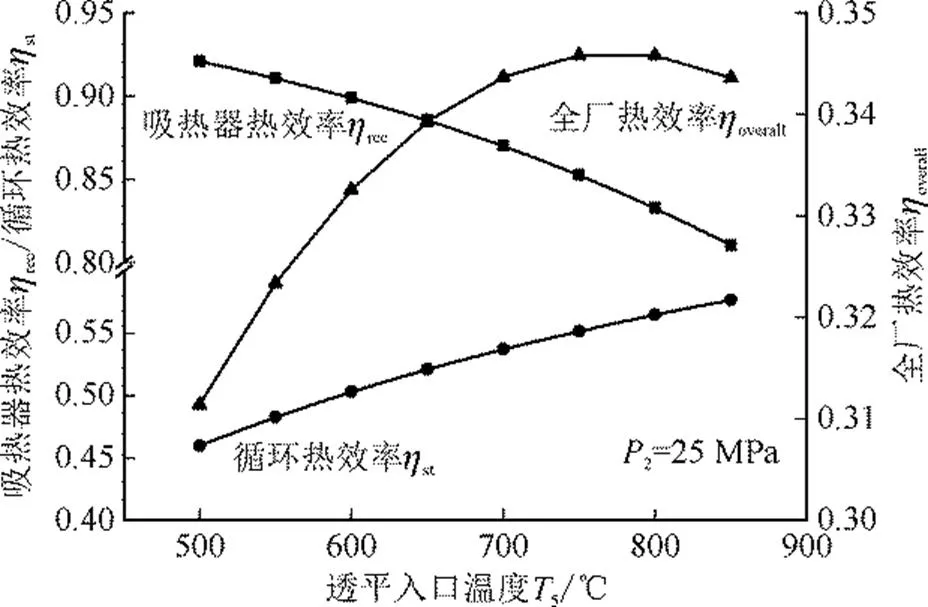
图6 热效率随透平入口温度的变化

2.4 全厂热效率优化

1）参数2、5确定

根据上述讨论，每组主压缩机出口压力2和透平入口温度5都会对应一个最佳循环压比c,opt。当参数2和5确定时，利用步进法可直接计算c,opt。本文通过正交试验法，计算了主压缩机出口压力20~35 MPa、透平入口温度500~850 ℃范围内最佳循环压比c,opt，图7为循环压比优化结果。

图7 循环压比优化结果

为了更好地显示循环压比变化规律，将其转化为对应的最佳主压缩机入口压力1,opt，在此温度和压力范围内，最佳主压缩机入口压力可以根据插值进行工程计算。

2）参数2确定

不同的主压缩机出口压力2对应一组最佳循环压比c,opt和最佳透平入口温度5,opt，使得全厂热效率达到最大。当2确定时，利用优化算法可以计算c,opt和5,opt。本文采用遗传算法工具包以全厂热效率最大为优化目标，对透平入口温度和循环压比进行优化计算，结果见表3。

表3 透平入口温度和循环压比优化结果

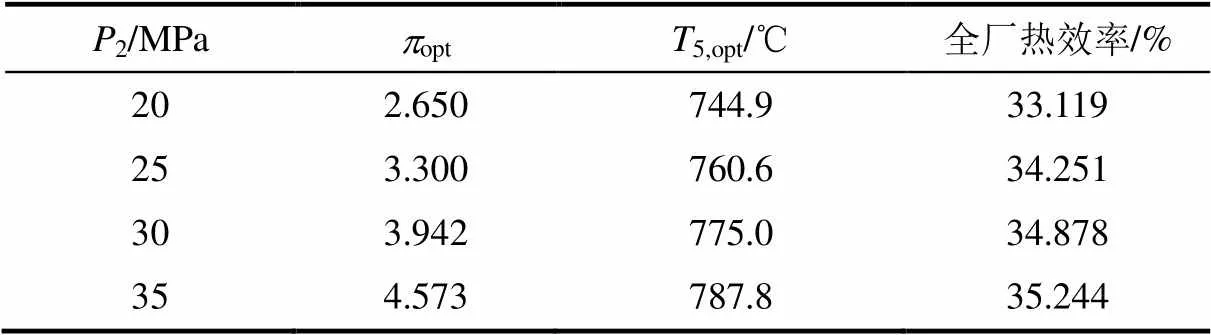
Tab.3 The optimization results for turbine inlet temperature and pressure ratio

3 结 论

1）随着循环压比的增大，全厂热效率的变化趋势会出现一个最大值，最佳循环压比随着主压缩机出口压力的升高而增大，主压缩机出口压力每提升5 MPa，全厂最佳热效率可以提升约0.5~1.0个百分点。

2）随着透平入口温度的升高，动力循环热效率增大，吸热器热效率减小，全厂热效率出现先增大后减小的变化规律，且在透平入口温度750 ℃附近存在最大值。

3）提出2种针对超临界二氧化碳塔式太阳能热发电系统的优化设计方案，并给出了在其他参数一定时，主压缩机入口压力20~35 MPa，透平入口温度500~850 ℃范围内，循环压比和透平入口温度的优化值。

［1］ 杜尔顺, 张宁, 康重庆, 等. 太阳能光热发电并网运行及优化规划研究综述与展望[J]. 中国电机工程学报, 2016, 36(21): 5765-5775.DU Ershun, ZHANG Ning, KANG Chongqing, et al. Reviews and prospects of the operation and planning optimization for grid integrated concentration solar power[J]. Proceedings of the CSEE, 2016, 36(21): 5765-5775.

［2］ 周昊, 裘闰超, 李亚威. 基于超临界CO2布雷顿再压缩循环的塔式太阳能光热系统关键参数的研究[J]. 中国电机工程学报, 2018, 38(15): 4451-4458. ZHOU Hao, QIU Runchao, LI Yawei. Parameter analysis of solar power tower system driven by a recompression supercritical CO2Brayton cycle[J]. Proceedings of the CSEE, 2018, 38(15): 4451-4458.

［3］ TURCHI C S, MA Z W, NEISES T, et al. Thermodynamic study of advanced supercritical carbon dioxide power cycles for high performance concentrating solar power systems[C]//Proceedings of the ASME 6th International Conference on Energy Sustainability Collocated with the ASME 10th International Conference on Fuel Cell Science, Engineering and Technology. San Diego, California, USA: ASME, 2012: 75-383.

［4］ IVERSON B D, CONBOY T M, PASCH J J. Supercritical CO2Brayton cycles for solar-thermal energy[J]. Applied Energy, 2013, 111(4): 957-970.

［5］ MILANI D, LUU M T, MCNAUGHTON R, et al. A comparative study of solar heliostat assisted supercritical CO2recompression Brayton cycles: dynamic modeling and control strategies[J]. The Journal of Supercritical Fluids, 2017, 120: 113-124.

［6］ 朱含慧, 王坤, 何雅玲. 直接式S-CO2塔式太阳能热发电系统光-热-功—体化热力学分析[J]. 工程热物理学报, 2017, 38(10): 2045-2053. ZHU Hanhui, WANG Kun, HE Yaling. Thermodynamics analysis of solar thermal power tower systems integrated with the direct-heated supercritical CO2Brayton cycles[J]. Journal of Engineering Thermophysics, 2017, 38(10): 2045-2053.

［7］ 陈渝楠, 张一帆, 刘文娟, 等. 超临界二氧化碳火力发电系统模拟研究[J]. 热力发电, 2017, 46(2): 22-27. CHEN Yunan, ZHANG Yifan, LIU Wenjuan, et al. Simulation study on supercritical carbon dioxide thermal power system[J]. Thermal Power Generation, 2017, 46(2): 22-27.

［8］ 吴毅, 王佳莹, 王明坤, 等. 基于超临界CO2布雷顿循环的塔式太阳能集热发电系统[J]. 西安交通大学学报, 2016, 50(5): 108-113.WU Yi, WANG Jiaying, WANG Mingkun, et al. A towered solar thermal power plant based on supercritical CO2Brayton cycle[J]. Journal of Xi’an Jiaotong University, 2016, 50(5): 108-113.

［9］ ZHU G D, LIBBY C. Review and future perspective of central receiver design and performance[C]//Solarpaces: International Conference on Concentrating Solar Power & Chemical Energy Systems. AIP Publishing LLC, 2017.

［10］ WILLIAMS D F. Assessment of candidate molten salt coolants for the NGNP/NHI heat-transfer loop[R]. Oak Ridge: Oak Ridge National Laboratory, 2006: 13-16.

［11］ XIN L, WEIQIANG K, ZHIFENG W, et al. Thermal model and thermodynamic performance of molten salt cavity receiver[J]. Renewable Energy, 2010, 35: 981-988.

［12］ GARG P, KUMAR P, SRINIVASAN K. Supercritical carbon dioxide Brayton cycle for concentrated solar power[J]. The Journal of Supercritical Fluids, 2013, 76: 54-60.

［13］ SARKAR J, BHATTACHARYYA S. Optimization of recompression S-CO2power cycle with reheating[J]. Energy Convers Manage, 2009, 50(8): 1939-1945.

［14］ PADILLA R V, TOO Y C S, BENITO R, et al. Exergetic analysis of supercritical CO2Brayton cycles integrated with solar central receivers[J]. Applied Energy, 2015, 148: 348-365.

［15］ XU C, WANG Z F, LI X, et al. Energy and exergy analysis of solar power tower plants[J]. Applied Thermal Engineering, 2011, 31(17/18): 3904-3913.

［16］ MARK O M, ERIC W L, MARCIA L H. The Refprop database for the thermophysical properties of refrigerants[C]. 2003 International Congress of Refrigeration. Washington D.C.: NIST, 2003.

［17］ 吴闯, 王顺森, 王兵兵, 等. 超临界二氧化碳布雷顿循环燃煤发电系统仿真研究[J]. 中国电机工程学报, 2018, 38(21): 6360-6366. WU Chuang, WANG Shunsen, WANG Bingbing, et al. Simulation research on coal-fired power generation system using a supercritical carbon dioxide Brayton cycle[J].Proceedings of the CSEE, 2018, 38(21): 6360-6366.

Simulation and optimization of solar thermal tower power system with indirect-heated supercritical CO2 Brayton cycles

HE Xinxin, XUE Zhiheng, CHEN Huiyong, WANG Weifeng

(Xi’an Thermal Power Research Institute Co., Ltd., Xi’an 710054, China)

The mathematic model for tower type solar thermal power generation system with indirect-heated supercritical CO2 Brayton cycles was established. The system is simulated under conditions with different turbine inlet temperatures, main compressor outlet pressures and pressure ratios, and the variation law of thermal efficiency of the whole plant was analyzed. The results show that, along with the rising of the turbine inlet temperature, the thermal efficiency of the whole plant first increases and then decreases, and it would reach the maximum in the vicinity of 750 ℃. With an increase in the circulating pressure ratio, the thermal efficiency of the whole plant increases firstly and then decreases. There exists the optimal pressure ratio for different outlet pressures of the main compressor and different outlet temperatures of the turbine. Furthermore, two optimization proposals of the system were proposed, and the optimized parameter values are given: the main compressor inlet pressure of 20~35 MPa, and the turbine inlet temperature of 500~850 ℃.

supercritical, carbon dioxide, tower type, solar energy thermal power generation, cavity receiver, parameter optimization

TM615.1

A

10.19666/j.rlfd.201902014

何欣欣, 薛志恒, 陈会勇, 等. 间接式超临界二氧化碳塔式太阳能热发电系统仿真优化[J]. 热力发电, 2019, 48(7): 53-58. HE Xinxin, XUE Zhiheng, CHEN Huiyong, et al. Simulation and optimization of solar thermal tower power system with indirect-heated supercritical CO2Brayton cycles[J]. Thermal Power Generation, 2019, 48(7): 53-58.

2019-02-19

何欣欣(1992—)，男，硕士，工程师，主要研究方向为热力系统及汽轮机性能，hexinxin@tpri.com.cn。

（责任编辑 杜亚勤）