理想弹塑性悬臂梁双重非线性问题的优化算法

林祖宏，尤 超，谭启明

与纯弯曲悬臂梁的不同，理想弹塑性悬臂梁在横向载荷作用下，悬臂梁横截面上的剪力不再为零，所以要考虑剪切变形的影响[1]，这也是比纯弯曲悬臂梁更为复杂之处。对于双重非线性问题，常用的求解方法是有限元方法，即从初始位置开始，逐步递增荷载的方式，并在每个荷载步段通过牛顿-拉斐尔法逼近平衡状态[2-3]。而本文的做法是取结构变形后的平衡状态为研究对象，应力-应变关系采用理想弹塑性模型，并考虑剪切变形的影响，最后确定理想弹塑性悬臂梁双重非线性分析的优化问题[4-9]，编制相应优化程序求解转角和变形，并结合典型案例与有限元法计算结果进行比较[10-12]，验证本文提出的优化算法的正确性和有效性。

1 建立理想弹塑性悬臂梁力学模型

悬臂梁的横截面为矩形，梁长L，宽b，高2h，刚度EI，屈服强度Y，受集中力Px、Py作用，其受力图如图1所示。

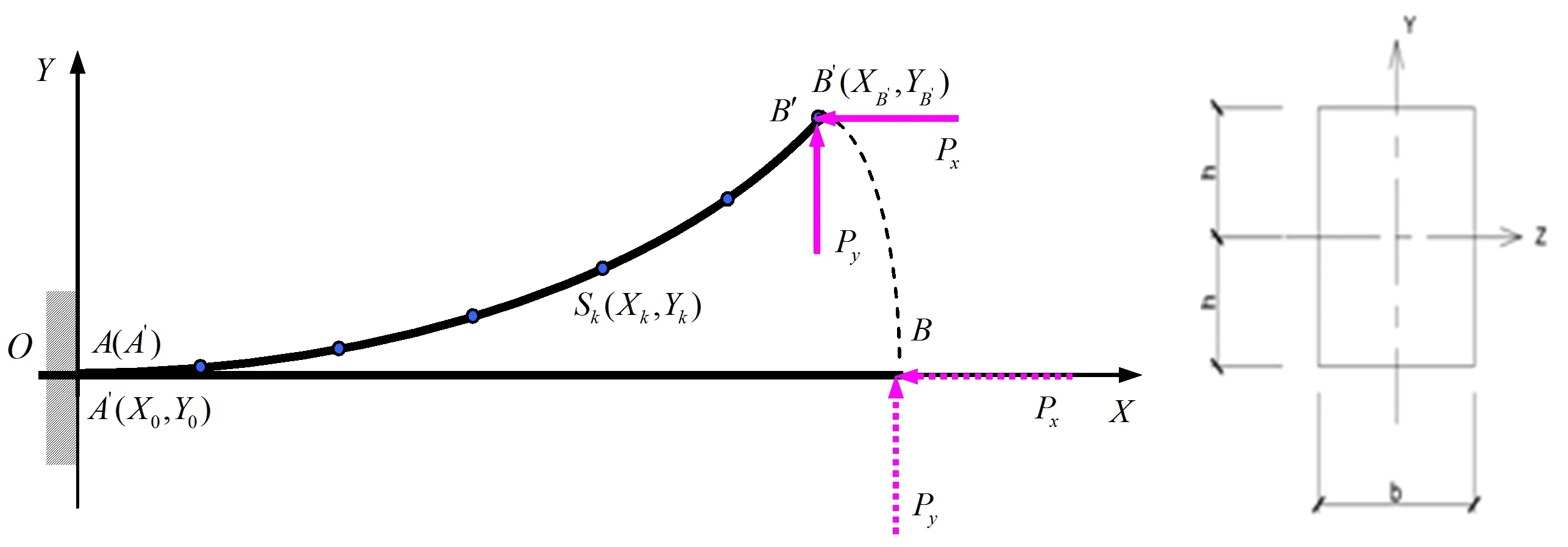
图1 理想弹塑性悬臂梁变形前后的平衡状态图

变形前，理想弹塑性悬臂梁固定端的受力为：

(1)

变形后，理想弹塑性固定端的受力为：

(2)

发生弹塑性变形后，变形如图2所示，阴影部分为弹塑性变形区，其他部分为弹性变形区，圣维南定力依然成立，应力-应变关系采用理想弹塑性结构模型，其本构方程为：

(3)

式中：ε为应变，σ为应力，E为弹性模量，λ是一个非负的参数。

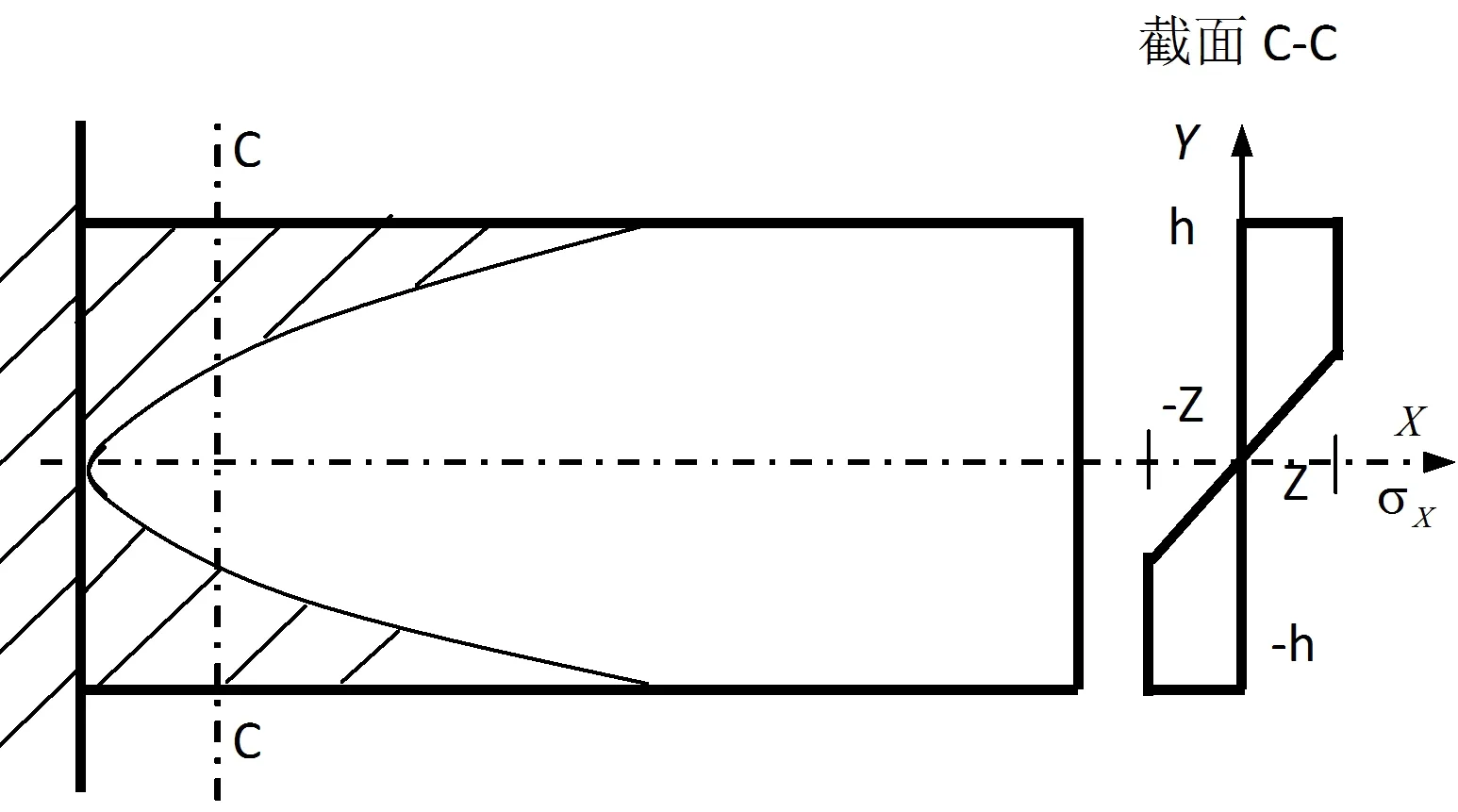
图2 理想弹塑性悬臂梁的弹塑性变形分布图

2 各微段在局部坐标系下受力分析

理想弹塑性悬臂梁发生弹塑性变形后，见图1，端点坐标分别是A′(0,0)、B′(XB′,YB′)，将悬臂梁分为n个微段，每个微段的长度是Δl=L/n，设整体坐标系为OXY，则微段端点在整体坐标系下的坐标是Sk(Xk,Yk),k=0,1,2,…,n。

图3 第k个微段变形后的平衡状态图

对变形后第k个微段进行内力分析，见图3，左端点坐标是Sk-1(Xk-1,Yk-1)，右端点坐标是Sk(Xk,Yk)，以微段左端点坐标的切线和法线为xk轴和yk轴，建立局部坐标系xkoyk，每个微段的变形符合胡克定律，由材料力学[13]可知：

(4)

第k个微段的内力为：

(5)

理想弹塑性悬臂梁在横向载荷作用下，横截面上的剪力Qk不再为零，此时要将剪切变形的影响考虑进来，剪切变形可由下式求得。

(6)

式中：K为与横截面形状有关的剪力修正系数。

发生弹塑性变形后中心轴线处的曲率，由本构方程，屈服强度Y，εY=Y/E和kY=εY/h得出：

MY=kYEI=YI/h

(7)

式中：kY为达到屈服条件时中心轴线处的曲率。

可得理想弹塑性材料悬臂梁第k个微段的曲率为：

(8)

则第k个微段的变形关系式为：

(9)

3整体坐标系下递推关系式的建立

在整体坐标系下，Sk点的变形与转角由Sk-1点和第k个微段的变形与转角共同决定，若第k个微段的转角与变形分别为Δθk、Δxk、Δyk，则Sk点的变形由下面递推关系式得到：

(10)

3 计算优化问题与目标函数

(11)

构建以自由端B′点未知坐标为设计变量的目标函数：

(12)

4 算例分析

理想弹塑性悬臂梁结构参数如下：横截面为矩形，高h=0.01m，宽b=0.05m，梁长L=1m，弹性模量E=100.0MPa，泊松比μ=0.3，屈服强度Y=1.0MPa，剪切模量G=1.0MPa，惯性矩IZ=[0.05×0.023]/12=3.33×10-8。采用本文优化算法和有限元方法分别对典型算例进行计算，并对计算结果进行数值模拟分析。

算例1竖向荷载Py作用在悬臂梁自由端，用本文优化算法和有限元软件分别计算Py的八种荷载情况，并将两种方法的计算结果列于表1中。

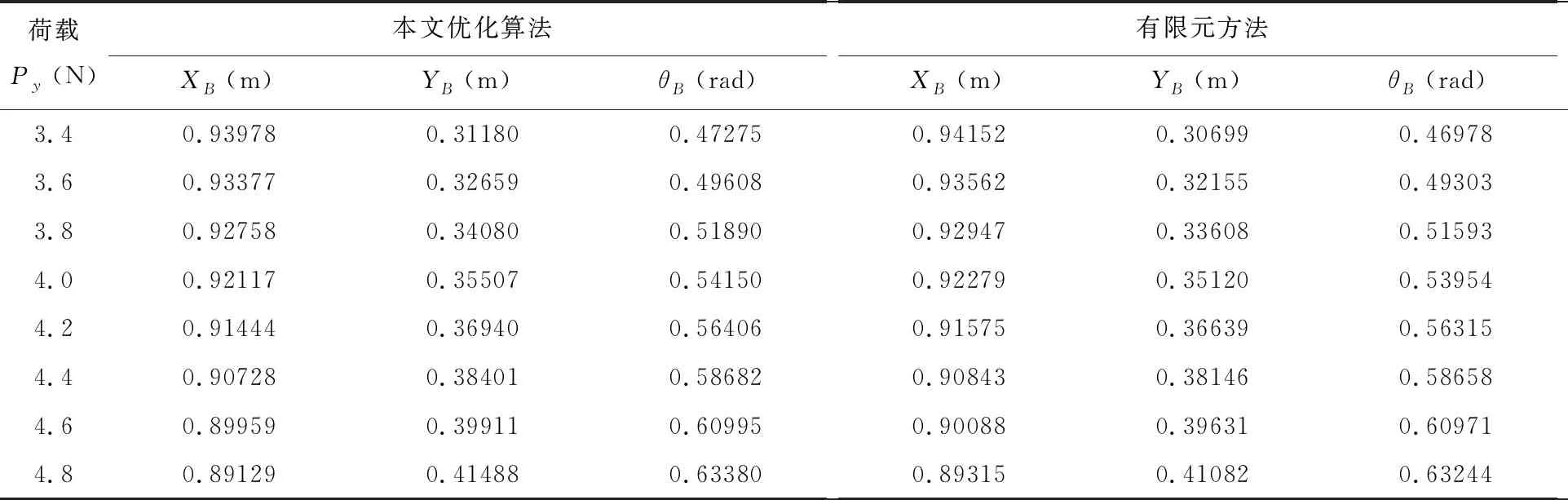
表1 Py作用下理想弹塑性悬臂梁变形结果

图4为在不同竖向荷载作用时，本文优化算法得到的变形后理想弹塑性悬臂梁的平衡状态图。

图4 在不同Py作用下，本文算法得到的理想弹塑性悬臂梁变形图

图5为竖向荷载为Py=4.8N时，分别采用本文优化算法和有限元方法得到的转角和挠度变形曲线图。

图5 Py=4.8N时，本文算法和有限元方法得到的理想弹塑性悬臂梁变形图

算例2荷载Px、Py分别作用在悬臂梁自由端，用本文优化算法和有限元软件分别计算Py=Px的八种荷载情况，并将两种方法计算出的变形和转角列于表2中。

图6为在不同Px、Py作用时，本文优化算法得到的变形后理想弹塑性悬臂梁的平衡状态图。

图7为Px=Py=4.8N时，分别采用本文优化算法和有限元方法得到的转角和挠度变形曲线图。

从图5和图7的转角和挠度曲线图可以看到，采用本文优化算法和有限元方法的计算结果具有很好的一致性，进而说明本文提出的优化算法在求解理想弹塑性悬臂梁双重非线性问题具有有效性和正确性。

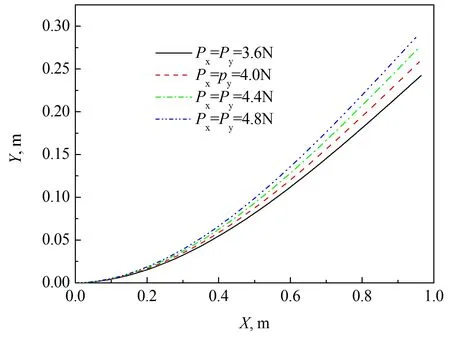
图6 在不同Px、Py作用下，本文算法得到的理想弹塑性悬臂梁变形图

5 结束语

本文研究了理想弹塑性悬臂梁双重非线性的问题，对结构变形前后的平衡状态，进行受力分析，建立理想弹塑性悬臂梁力学模型，构建端点未知的目标好函数，确定结构变形的优化问题。通过计算典型实例，从转角和变形对比图可以看到，采用本文优化算法和有限元方法的计算结果具有很好的一致性，进而验证了本文优化算法在求解理想弹塑性悬臂梁双重非线性问题上的有效性和正确性，具有一定的推广前景。

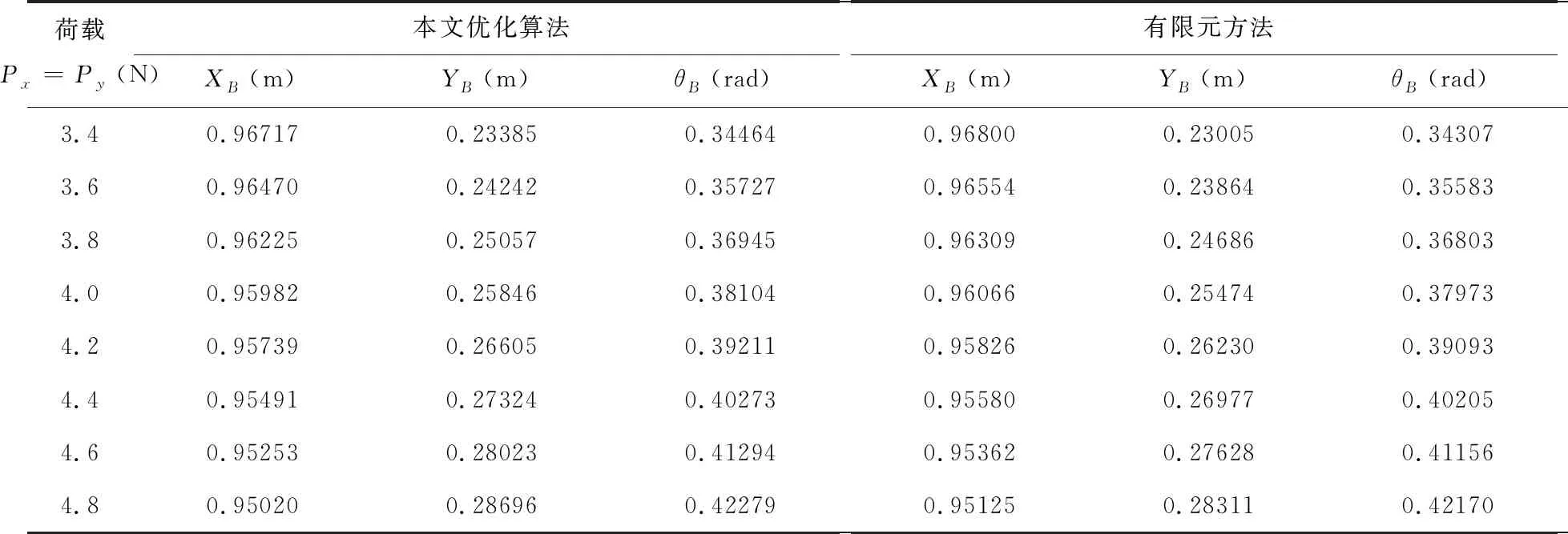
表2 Px=Py作用的理想弹塑性悬臂梁变形结果

图7 Px=Py=4.8N时，本文算法和有限元方法得到的理想弹塑性悬臂梁变形图