外磁场作用下双粒子体系的能级研究①

裴魏魏， 张海丰, 刘明达， 韩海生*

(佳木斯大学a.理学院，b.附属第二医院，黑龙江 佳木斯 154002)

0 引 言

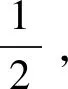
1 不加外磁场时体系的能级和本征态讨论

为讨论问题方便，取ћ=1，并取磁场方向为z轴，则体系的能量算符为

H=As1·s2+Bμs1Z

(1)

当B=0时，H=As1·s2，而

(2)

能量本征态可以取为(S2,SZ)的共同本征态，记为|SSz〉。如以(S1z,S2z)的共同本征态|S1z,S2z〉作为基矢，则

(3)

其中〈S1zS2z|SSZ〉之值可利用CG系数表而写出，结果为

(4a)

(4b)

(4c)

(4d)

(4e)

(4f)

其中等号左侧为(SSZ)表象，右侧为(S1zS2z)表象。

2 忽略自旋相互作用时强磁场中体系的能级

磁场很强时，粒子间相互作用As1·s2可以略去

H≈Bμs1z=Bμ，0，-Bμ

(5)

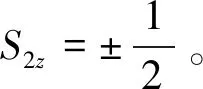
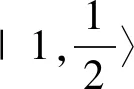
3 体系能级的精确解微扰论结果比较分析

下面将求体系能级的精确解，并分别就强磁场和弱磁场两种条件给出能级的近似公式，最后同微扰论的结果进行比较。

以|S1z,S2z〉作为基矢，计算As1·s2的矩阵元时利用了(4)式，例如

(6a)

(6b)

所以

(7)

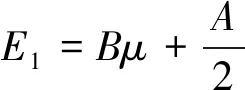
将矩阵对角化可得到其他四条能级。

(8)

(9)

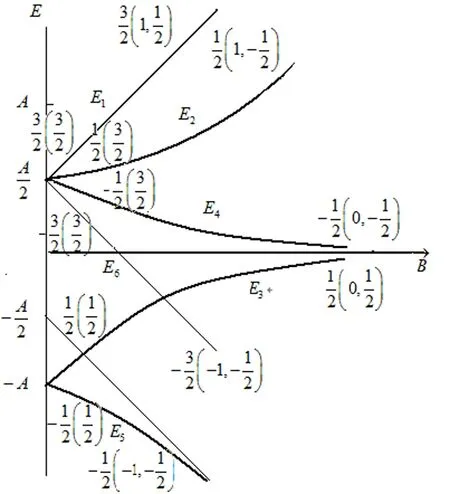
图1 能级随磁场B变化的示意图

3.1 强磁场

在强磁场中Bμ≫A，式(8)、(9)作近似展开后，得到

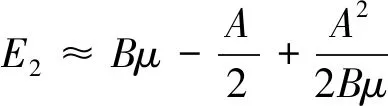
(10)

这些结果与按照二级微扰理论公式所得结果一致。

3.2 弱磁场

在弱磁场中Bμ≪A，式(8)、(9)作近似展开后，得到

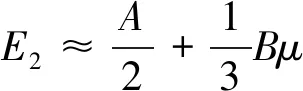
(11)

这些结果相当于简并态微扰论一级近似。

4 能级随磁场B变化的示意图

设μ,A>0，能级随磁场B变化的示意图如图1所示。

5 结 论