水利工程监理评价与预警研究

余明国，钟慧敏

(上饶市水利水电工程建设监理中心，江西 上饶 333300)

监理单位作为水利工程中不可或缺的一部分，是重点的监管对象之一，有效准确开展对监理管理工作的监督，成为建立监管部门最重要的任务之一，关系着工程本身的质量和安全[1]。

近年来，水利工程管理中暴露的问题逐渐突出，各单位之间的管理水平参差不齐，导致工程进度、质量、安全进展低效[2- 4]。为发挥监理在水利工程建设中应有的控制性作用，必须努力提升其整体行业的管理水平并建立一套行之有效的评价机制[5]；同时，需要监理单位内部加强管理，形成长效的内部评审及约束机制，才能杜绝或者减少在工作过程中的某些错误行为[6]；庹朝洪[7]，高翔[8]，王巧丽[9]等针对不同的工作内容，对监理的管理理念、措施和手段进行了详细分析；赵培等则针对目前水利工程建设施工监理工作的现状，基于AHP方法，建立起评价指标体系和评价阈值，对水利工程建设监理合同管理进行了探讨[10]。

本文立足于当前水利工程建设监理管理中的主要工作模式[11]，基于模糊理论和遗传BP神经网络方法，建立起监理工作的综合评价和预警模型，可为监理单位自查、监管单位监督提供一定的理论和实践作用。

1 监理单位概况

江西某水利监理公司成立于2000年，是一个自负盈亏的股份制企业，经水利部批准2001年7月颁发丙级资格水利工程建设监理单位，2004年10月经水利部批准核定为乙级资格工程建设监理单位，2007年9月经水利部批准核定为甲级资格工程建设监理单位，可承担各等级水利工程施工监理业务，现有注册监理工程师及监理员共200余人。公司成立以来，截止2018年底，已签定监理合同实施和正在实施的水利工程1000余项，其中中型水库除险加固工程30余座、大型灌区5座、城市防洪工程30余项、大中型水闸、抬水坝等，在各项水利工程监理方面积累了较为丰富的经验，产生了较好的经济效益。

2 模型建立

2.1 模糊评价模型

根据国家相关法律法规，同时参考监理相关规范，确定了以资质支撑材料、公司管理、建立业务、信息管理、项目监理机构应备文件、现场监理机构以及监理工作等7个指标为一级指标，涵盖包括财务、人员、合同、设备等42项因子的二级指标，建立起相应的综合评价模型，见表1。

根据模糊评价理论，其主要的计算过程概述为：

(1)确定指标权重，即通过分析赋权，获得一级指标权重W(1)=(w1，w2，…，w7)和二级指标权重=(w11，w12，…，w713)；

(2)确定评价矩阵，实现管理水平从定性到定量的描述，即有：

(1)

式中，i—一级指标；m—二级指标对应一级指标项数。

(3)综合评价：通过指标权重和评价矩阵，最终可以得到监理单位管理水平的模糊综合评价值：

M=Q·W1

(2)

再通过矩阵转化，最终得到模糊综合评价量化值：

E=M·TT

(3)

式中，E—综合评价值；T—评语集矩阵，且T=[9，7，5，3，1]

表1 综合评价指标体系的建立

2.2 BP预警模型

首先，以42个二级指标因子为输入变量建立三层BP神经网络，并通过经验公式：

(4)

式中，N—隐含层节点数；m、l—分别表示输入和输出节点数)计算得到隐含层的节点数为12。

最终建立40- 12- 1的三层BP神经网络，如图1所示；其次，对输入指标进行标准化处理，使其量化值处于[0，1]之间，并选择Log-Sigmoid函数

f(x)=1/(1+e-1)

(5)

作为预警模型的激励函数；经过网络初始化，对隐含层和输出层进行计算，并基于动量改进算法对权重值和阈值进行不断的更新；当网络输出函数与目标函数值相差在一定精度范围内时，计算终止，得到最终的目标函数E:

(6)

式中，E—目标函数；y—期望输出；t—输出层输出值。

图1 三层BP神经网络

将目标函数作为预测模型函数，同时对模糊理论评价值的时间序列进行滚动预测，建立相应的预警图，如图2所示。预警图根据评价值的大小，分为五个等级，即：优秀级、良好级、过渡级、低警戒级以及警戒级，可以通过走势图对监理单位的管理水平进行直观了解和预测，可以起到工程建设过程中的事前预防控制，为决策者提供分析依据，并提醒其及时采取相应的措施，尽量避免和减少管理异常的情况发生，减少发生在工程中的事故和错误。

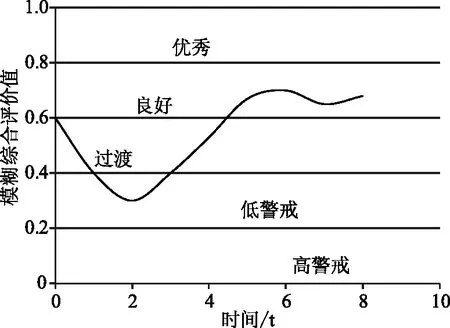
图2 预警评价分区图

3 结果分析

3.1 模糊评价情况

通过双随机抽取检查，对该监理单位进行打分，然后进行权重组合，分别得到：二级指标权重向量为：W(2)=(0.005，0.010，0.015，0.020，0.028，0.014，0.025，0.022，0.020，0.030，0.017，0.024，0.028，0.025，0.019，0.036，0.021，0.040，0.028，0.022，0.024，0.020，0.014，0.090，0.054，0.036，0.008，0.013，0.012，0.012，0.012，0.033，0.036，0.039，0.045，0.024，0.030，0.015，0.021)，一级指标额权重值为：W(1)=(0.05，0.14，0.15，0.10，0.08，0.18，0.30)。

构建各一级指标的评价矩阵：

(5)

(6)

(7)

(8)

(9)

(10)

(11)

将权重值w和评价矩阵Q代入公式(2)，得到M=(0.0，62，0.229，0.353，0.241，0.116)，最大值为0.353，介于0.2～0.4之间，故该单位2018年的整体管理水平为一般，且模糊综合评价的量化值为：

E=M·TT=4.76

(12)

3.2 预警情况

基于上述模糊理论评价方法，对该监理单位的2011—2018年的管理水平E依次进行计算，并进行归一化处理，得到该监理单位管理水平评价值的时间序列情况，见表2。

表2 管理水平模糊评价值时间序列表

将2011—2016年数据作为训练值，2017—2018数据作为检测值，并设定学习速率为0.2，动量因子为0.2，目标函数误差值为0.01，最大训练步数为10000，运用MATLAB数值分析工具，对该监理单位的管理水平进行BP神经网络计算，得到模型输出值与评价值之间的相关关系，如图3所示。从图中可以看到：基于BP神经网络模型的计算结果与评价结果基本保持一致，平均误差仅为0.0041，小于0.01，表明该模型可以很好地预测建立单位的管理水平；同时，从图中反馈的信息还可以看到，2011—2015年，该监理单位的管理水平整体处于良好状态，而2016—2017年，则处于过渡状态，这对该单位的长远发展的影响敲响了警钟，预示着该单位需要通过不断改革、不断创新来努力摆脱这一局面，2018年，在经过不断的产业调整、人员调整和体制改革后，该监理单位管理水平有所提高重新回到良好管理水平状态；通过数据分析，忽略外部其它环境因素的影响，对2019—2020年的管理水平进行预测，分别达到0.8和0.85，可见，该监理单位的管理水平将逐渐步入优秀级，可以预见该单位未来几年将进入持续良好的黄金发展期。

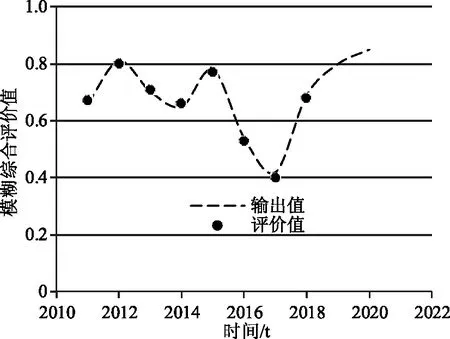
图3 输出值与评估值对比

4 结论

以江西某监理单位为例，采用文中建立的模糊综合评价模型，对该单位近年管理水平进行综合评价和预警分析，结果显示：综合评价模型的输出结果与评价结果平均误差小于0.01，模型计算结果具有可行性和合理性，该单位目前正处于黄金发展期；研究成果对监理单位自查、监管单位监督提供了可靠的决策手段；限于统计数据有限，本案例仅对该监理单位近10年的管理水平进行了评估和预测，若能增加训练和检测值数目，可使研究结果更加贴近实际，可在以后工作中逐步开展和完善。