深矿井锚网支护方案优化分析
何 光
(陕西麟北煤业开发有限责任公司园子沟煤矿,陕西 宝鸡 721505)
0 引言
目前我国开采深度超过1 000 m的生产(在建)矿井达到47处[1]。在高地应力情况下,煤岩体发生了显著的变化,从脆性变为弹性,岩体内显现出明显的流变、蠕变和膨胀特征[2-3]。高地应力和煤岩体特征决定了深部开采矿井将会遇到一些动力灾害,这些灾害主要发生在巷道附近。因此,深部开采的关键和主要问题就是巷道支护。
锚杆支护技术在中国主要矿区的大面积传播和应用,产生了巨大的技术和经济效益。目前,国内外锚杆支护设计方法可分为3类,即:工程类比法、计算方法和数值模拟方法[4]。工程类比法有很大的随意性,不能解决复杂的边界问题,因此,它的应用有限[5]。将计算方法和数值模拟方法相结合,采用计算方法,确定数种支护方案,然后采用数值模拟方法确定深矿井煤巷最优的锚杆支护方案,在严格遵守所提出的施工管理措施的基础上,巷道断面变形将得到有效控制。
1 回采巷道锚杆阻力和巷道表面位移监测
1.1 矿井回采巷道锚杆阻力和表面位移监测
矿井位于吉林省西部,产量3.0 Mt/a,地表标高为+521.0 m,三水平标高为-700 m,目前开采深度已经超过1 000 m。-650区段回风平巷采用锚网支护方式,锚杆长度为2.5 m,直径为20 mm,锚杆间排距为0.8 m×0.8 m。锚索采用螺纹钢,直径为15.4 mm,长度为6.0 m,间排距为2.4 m。在巷道掘进过程中,发现巷道表面变形情况严重,巷道四周向内侧臌包严重。因此,有必要对巷道表面位移和锚杆阻力进行测试,以便于判断围岩的稳定性。
在-650 m回风平巷内设置1号和2号两个测量断面,距离为20 m左右[6]。1号测量断面靠近掘进面,距离为12 m左右。每个测量断面布置5个锚杆测力计,锚杆阻力可以直接从锚杆测力计读出。测量结果表明,巷道右帮和右顶角锚杆的阻力增加量远比其他部位大,其原因可能是岩体应力大部分被回采巷道右侧的煤壁承担所致。据此可推断,巷道左侧煤壁已经压裂,浅部离层已经出现。
巷道表面位移测量结果表明,巷道顶底板距离和巷道宽度在12 d后倾向于稳定。断面顶底帮移近量均为50 mm。1号断面和2号断面顶底板移近距离分别为140 mm和65 mm。巷道表面变形如此大,因而应该采取措施控制变形量。
通过以上分析,再结合现场实际观察和测量,可以得出结论,-650 m回风平巷锚网支护参数应该进行优化,以便于更好地适应深部开采的需要。
1.2 巷道围岩松动圈测量
实践已经证明,松动圈对巷道的稳定性和巷道支护程度具有密切的联系[7]。松动圈的测量对于选择合理的支护方法和支护参数,减少巷道维护成本具有重要的作用。实践中采用BA-Ⅱ型松动圈测试仪测定松动圈。首先,在测点巷道左帮、右帮和顶板钻3个测量孔,注水后放入仪器进行测量,钻孔布置如图1所示,测量结果如图2所示。结果表明,巷道左帮、右帮和顶板的松动圈分别为1.6 m、1.8 m和1.5 m。按照围岩分类标准,巷道所处围岩属于大松动圈围岩[8]。松动圈测量结果如图2所示,由于围岩中总存在硬的夹层,或者是弱面、裂隙带等,这将会造成得到的“孔深-速度”曲线带有向上或者向下的尖点,判断松动圈时,要剔除这些异常点,从总曲线的总体趋势上判断。
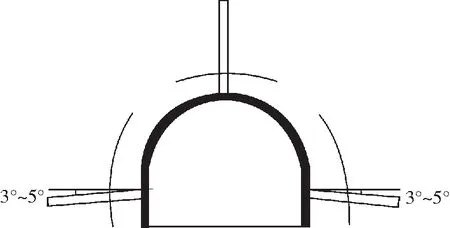
图1 松动圈测试时的钻孔布置

图2 炮孔深度和波速曲线
2 锚杆和锚索支护参数设计
由于巷道的松动圈范围为1.5~1.8 m,所以锚杆和锚索支护参数应该按照组合拱理论进行设计[9]。
2.1 锚杆支护参数确定
根据相关文献,可用下式计算锚杆参数[10-11]
L=L1+L2+L3
(1)
式中:L—锚杆长度,m;L1—锚杆的外露长度,m;L2—锚杆的有效长度,m;L3—锚杆的锚固段长度,m。
通常L1=0.1 m,L2应大于等于松动圈尺寸,L3=0.3~0.4 m。
m≤0.5L
(2)
m≤1.1
(3)
L2=b+m
(4)
式中:m—锚杆间排距,m;b—组合拱厚度,m。b根据经验取值,对于Ⅳ类围岩,b=0.9;对于V类围岩,b=1.1;对于Ⅳ类围岩,b=1.4,此处b=0.9。
(5)
式中:d—锚杆间排距,mm。按照上面的公式,经过计算,确定锚杆各参数为:L=2.2 m(目前采用2.5 m),d=22 mm(现在采用20 mm),m=0.8 m,b=1.0 m。
2.2 锚索参数确定
X=X1+X2+X3
(6)
式中:X—锚索长度,m;X1—锚索外露长度,m;X2—锚索锚固长度,m;X3—潜在不稳定岩层高度,m。通常X1=0.2 m;X2等于巷道宽度。
s=3σ/(4B2γ)×k
(7)
式中:s—锚索排距,m;σ—每根锚索最低破断载荷,kN;γ—煤岩体积力,kN/m3;B—巷道宽度h,m;k—安全系数。此处σ=260 kN,γ=14.4 kN/m3,k=0.5。
m=0.85B/n
(8)
式中:m—锚索间距,m;n—排数。据以上公式,确定锚索参数:X=6.0 m,s=1.54 m,m=1.2 m。
3 不同支护方案的数值优化
按照以上计算,再结合目前掘进巷道所采用的支护方式,提出了3种可行的锚杆锚索支护方案,见表1。

表1 不同的支护方案
采用数值模拟软件FLAC3D,建立了锚杆锚索支护模型。模型的长、宽、高分别为45 m、20 m、50 m,总共分为301 995单元,55 063节点。

图3 垂直应力分布(方案1)
图3、图4和图5是各方案的垂直应力分布,从以上3图中可以看出,最大应力分别为24.4 MPa、27 MPa和27.9 MPa。显然第一种方案应力集中程度最低,巷道围岩应力状态较好。图6、图7和图8是水平位移分布,可看出最大的水平位移分别为204 mm、260 mm、280 mm。图9、图10和图11是垂直位移分布,可看出,顶板下沉量分别为173 mm、212 mm、243 mm。底板臌起量分别为318 mm、343 mm、381 mm。总体来说,方案1应力相对较小,变形量较小,是最佳的支护方案。
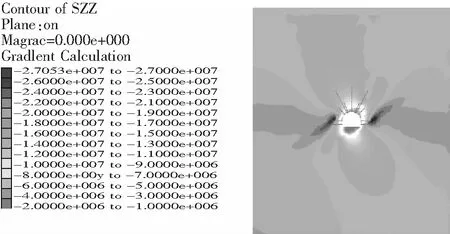
图4 垂直用力分布(方案2)

图5 垂直应力分布(方案3)

图6 水平位移分布图(方案1)

图7 水平位移分布图(方案2)

图10 垂直位移分布图(方案2)

图11 垂直位移分布图(方案3)

a-参数优化前巷道支护效果;b-参数优化后巷道支护效果图12 巷道支护效果前后对比图
采用方案1的支护参数1个月后,对巷道的变形情况进行了复查,掘进面后方12 m处巷道形状如图12中(b)所示,可见,改变了参数后,与原支护参数下巷道断面(a)比较,巷道断面变形得到了控制,扩大了巷道的有效断面。巷道表面位移监测数据表明,掘进前期巷道变两帮及顶底板变形量相对较快,后期处于缓慢变形阶段,最终达到相对稳定的状态。1号断面和2号断面顶底帮移近量均为35 mm,1号断面和2号断面顶底板移近距离分别为55 mm和35 mm。与原有方案对比,巷道表面变形明显收窄。
4 结论
(1)通过监测巷道表面位移和锚杆支护阻力,发现-650回风平巷巷道表面位移量很大,巷道围岩出现离层,支护方式需要改进。
(2)巷道左帮、右帮和顶板的围岩松动圈值测定结果表明,巷道围岩属于大松动圈围岩,在此基础上,采用组合拱理论设计了锚杆和锚索支护参数。
(3)在锚杆锚索支护理论计算和现场经验的基础上,提出了3种支护方案。采用FLAC3D数值模拟软件,对3种支护方案进行了数值模拟,提出了最优支护方案。实践表明,优化支护参数后,巷道断面变形得到了有效控制。

