四边形上一种线性双有理映射构造方法
吴 梦,陈 冲,王旭辉,钱毅加
四边形上一种线性双有理映射构造方法
吴 梦,陈 冲,王旭辉,钱毅加
(合肥工业大学数学学院,安徽 合肥 230009)
作为一种特殊的有理映射,双有理映射可应用于图像变形、等几何分析中区域参数化中。针对文献[1]通过几何方法构造四边形上的双有理映射,需要先确定权值再构造的问题,提出一种基于动直线的方法,可直接构造四边形上的双有理映射。此外,通过选择不同的参数,可以得到四边形上不同的双有理映射。验证可知,该方法满足文献[1]提出的权值比例关系,并通过实例说明了其有效性。
双有理映射;动直线;权值
双有理映射是一种特殊的有理映射,其映射与逆映射均为有理的。具体到二元有理映射情形,给定二元有理映射(,),若其满足:
双有理映射具有形式简单便于计算等特性,且在计算机图形学和几何设计中发挥着重要的作用[2],同时也在图像变形和图像修复上有着广泛的应用[3],HUDSON[4]基于Cremona变换讨论了二维有理映射的数学理论,但具体应用时需要考虑双有理映射的构造问题,这也是十分新颖的问题。近年来,文献[1]针对四边形情形,通过事先对四边形的顶点赋予适当的权值,提出了一种四边形上的双有理映射的构造方法,同时FLOATER[5]又从重心的角度出发,重新解释了在四边形上的双有理映射,并且给出了其逆映射的一般形式。文献[6]通过建立凸六面体的重心坐标,找到了满足特殊条件的权值的构造方法,给出了在凸六面体上的三线性映射为双有理映射。
动直线是由COX等[7]提出的,是一种解决曲面表示与计算的代数工具,在曲线曲面隐式化、坐标参数化以及奇点计算等方面有着广泛的应用[8]。
本文从动直线出发,不需要事先通过对顶点赋权值来构造四边形上的双有理映射,从而直接给出四边形上的一种双有理映射。
1 四边形上的双有理映射
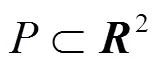
则定义在该四边形上的双线性映射为
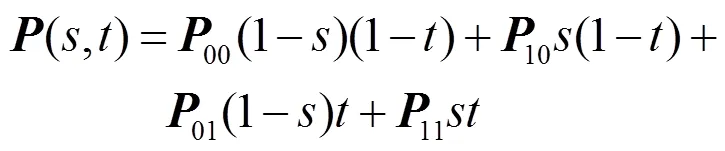
一般情况下,该映射不是双有理映射。然而,文献[1]将顶点赋上适当的权值w,通过计算,发现了权值需要满足的关系式,即当权值满足比例关系


