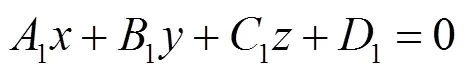一种基于RANSAC的点云柱状化轴线特征表示法

高春艳，申紫铭，张明路，田 颖

一种基于RANSAC的点云柱状化轴线特征表示法

高春艳，申紫铭，张明路，田 颖

(河北工业大学机械工程学院，天津 300130)

现有的三维地图构建算法多强调对地图构建的精确性，导致成图效率低、成本高。为了提高建立地图的效率，提出了一种对地标性物体进行圆柱体识别与提取并以其轴线特征作为地标构建简化地图的改进算法。基于随机采样一致算法（RANSAC）对点云模型中的待提取主体模型生成待估计圆柱模型并进行匹配，通过对单应性矩阵及其误差函数的计算得到迭代过程中的最佳阈值，以得到最佳匹配圆柱模型并提高提取效率，然后用所提取的圆柱轴线描述地标的空间位置，圆柱半径描述地标的空间几何信息。通过与传统RANSAC方法的仿真实验对比，证明该方法可以有效的精简地图，为后续识别地标路径规划奠定基础。

点云；三维地图；特征提取；RANSAC

目前三维点云地图常采用改进的ICP算法进行创建[1]，生成的三维地图精度较高，对环境的细节描述精细，所以存在着成本高、效率低、实时性差等问题。但在多路径规划与导航设计时并不要求地图过度精确，而是追求地图的实用性和快速响应，因此，需要对地图进行尽可能的简化，简化的三维地图构建的基础通常是点云特征提取的结果[2]。空间特征提取算法主要分为2大类[3]：①基于边界的算法，主要通过计算获得点云表面的法矢、曲率等微分几何变量的突变特性来提取特征，缺点是对噪声较为敏感，鲁棒性较低。②基于面域的算法，通过提取点云数据中具有共同属性的点集构造出稳定的生长区域进行生长，然后实现特征提取，主要有随机采样一致算法(random sample consensus，RANSAC)、最小中值算法和霍夫变换等[4]，虽然该类方法在提取特征时可以有效避免噪声的影响，但其实时性较差。平面特征提取的方法还有最小二乘法、特征值法等[5-8]，但其不能有效抵御异常值的影响且只能拟合平面，对空间形状的拟合效果较差。

为解决三维地图构建过程中实时性差，效率低等问题，本文提出了一种地标物体柱状化的方法，针对圆柱特征的提取在RANSAC算法[9]的基础上进行了改进，首先基于RANSAC算法在点云中随机生成一个圆，然后将圆形拉伸形成圆柱与点云模型进行匹配，当点云数据中的点到轴线的距离与半径符合条件的数量达到所设定的阈值时得到最终的匹配圆柱模型，为了减少匹配过程中的迭代计算次数，通过实验筛选出最佳阈值检测去除异常值并限定搜索区域。

1 基于RANSAC的物体柱状化轴线提取

1.1 基于RANSAC的物体柱状化处理

RANSAC算法是从一组数据集中通过迭代的方式匹配已给出的数学模型参数，最后通过估计局内点与模型的错误率来评估模型的精度[10]，因此传统的RANSAC算法具有一定的不确定性，其有一定的概率得到一个高精度的估计模型，但为了提高概率又必须提高迭代次数，影响计算效率，而迭代次数过低又很可能会因抽样不充分导出错误的估计模型[11]。

本文采用限制迭代次数上限的方法对圆柱体进行识别匹配。即先基于RANSAC给出匹配圆柱模型，通过阈值检测去除异常值以及限定搜索区域减小迭代次数，提高模型的精度。设为最少必要模型点个数，个点为局内点的概率为，点集的总数为，所有局外点数为N，随机选取一个点为局外点的概率为，则=N/。个点全部为局内点的概率为(1–), 1–(1–)表示个点中至少有一个为局外点的概率，则(1–(1–))表示个点恒不可能全部为局内点的概率，其应与1–相等[12-14]，即1–(1–(1–))，等式两边取对数得

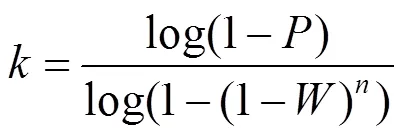
其中，k为算法的迭代次数(抽样次数)，迭代时n取大于k的值。k与N的关系如图1所示。

由图1可看出，在与确定的情况下，局外点率越大，迭代次数也就越大，为减少迭代次数，提高算法效率，在点的选取时应进行对搜索区域限定的自适应调整，降低局外点所占的比例。

改进的RANSAC算法提取圆柱的步骤如下：

步骤1.给定搜索区域，在该区域内选定一组待处理的点云集{1,2,···,P}，不共线的3个点确定一个圆，设圆所在平面为，随机选取其中的3个点{P,P,P|,,[1，]且≠≠}，如图2所示。

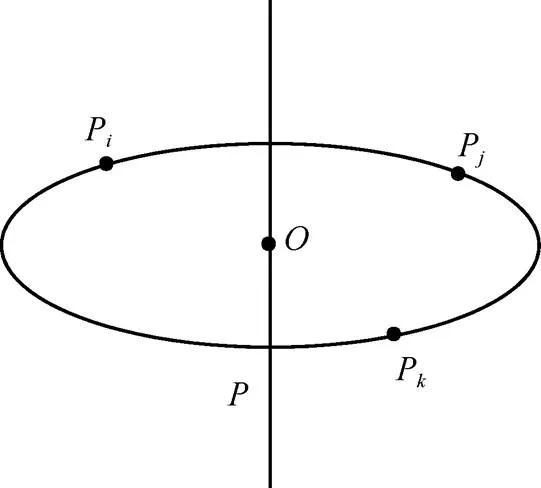
图2 圆与轴线的选择原理图

步骤2.计算3个点构成的圆的圆心坐标及半径(0，0，)，如图3所示，在圆心坐标处建立与圆所在平面垂直的轴线，生成与圆半径相等的圆柱体，计算点云集中的各点到轴线的距离l。

步骤3.设置符合条件的点的阈值，记录满足l∈[–,+]的点云集{1,2,···,Q}，当=/≥时，停止迭代。

步骤4.检验所得模型是否达到预期要求，若是，则进入下一步，否则回到步骤1。

步骤5.将得到的若干组数据进行比较，选出最符合预期要求的模型。

流程图如图4所示。

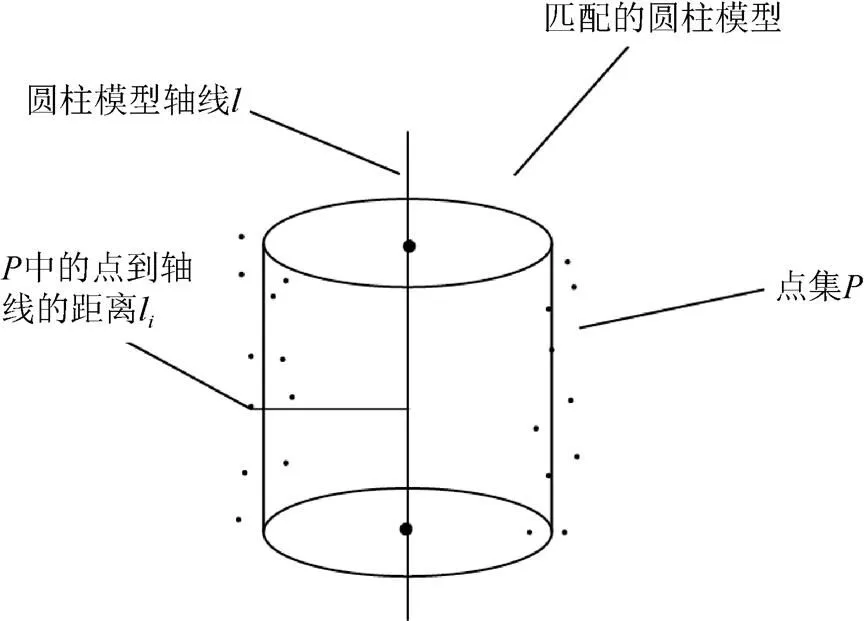
图3 点到轴线距离原理图

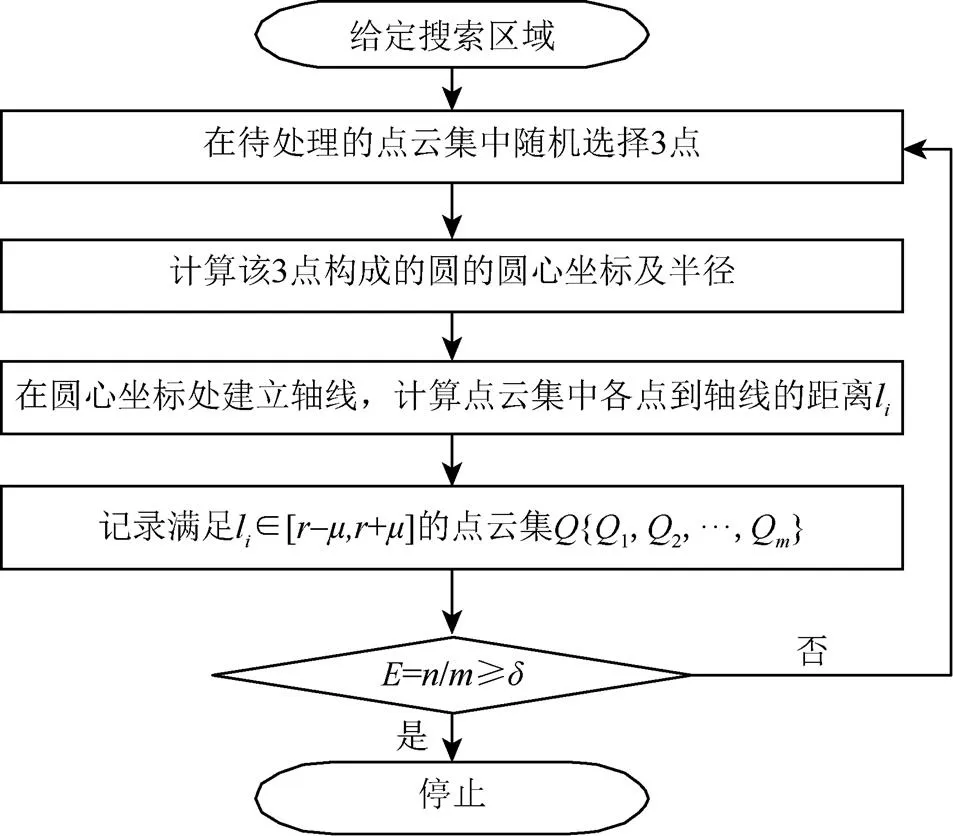
图4 圆柱模型提取流程图

1.2 柱状化轴线的提取

设在平面得到的3个点的空间坐标为1(1,1,1),2(2,2,2),3(3,3,3),圆心坐标为(0,0,0)，半径为。若得到轴线方程，需先求3个点所确定的空间圆的圆心坐标和半径，分析可得约束条件：

(1)1,2,3∈；

(2) |1|=|2|=|3|。

可得空间3点确定的平面方程为

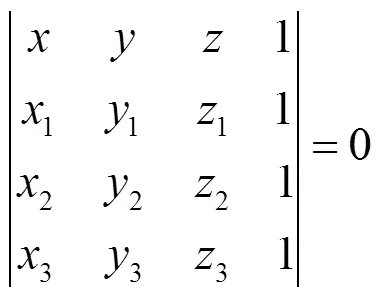
求解行列式得