血液静电泵的碟型阀门设计

孙冰 刘丽 张妍 田丰 齐景爱

1.天津市计量技术研究院，天津300192；2.河北工业大学，天津300401

一、引言

进入21世纪，科技突飞猛进，人工智能、5G芯片通讯、航天、基因细胞学、癌症治疗、克隆技术取得很大进步，但工程与医学由于知识鸿沟大，很少二者联合攻关。用静电泵可以实现与心脏节率一致的供血，这比恒压输血更适合人体血管。为此，利用作者工程学知识，再掌握粗淺的心脏供血数据，尝试制备救治心脏病人的装置做一点努力。因为心脏病是仅次于癌症影响人类生命的第二杀手。这是本文写作的初衷。

我们在文献[1-5]中完成了心脏手术时代用静电泵的设计，并讨论了微小型静电泵及其球型阀门设计。本文着重于血液静电泵碟型阀门设计。

静电泵碟型阀门与球型和锥塞型阀门不同，由于阀门打开时，会发生球、锥塞与丝网的碰撞，使血液血小板等破坏，造成血液质量严重恶化的后果，所以血液静电泵碟型阀门中放弃采用丝网结构，而采用图1所示的碟型阀门结构，其打开与闭合自动完成，本文讨论此中结构的合理性并作强度检验。

二、研究重点

根据文献[1]，心脏搏动时每次泵血量为70cm3～78cm3，血液静电泵实际由10个独立的微型血液静电泵组成，假设心率为60次/分，则可将每个静电泵流量设计为7.8cm3/s。阀门打开时，血流应全部流出。阀门打开与闭合由血液静电泵的激励电压控制，激励电压最小时，阀门自动打开，激励电压最大时，阀门自动关闭。血液静电泵的阀门管道为横向单向进、出口阀，其直径不能超过血液静电泵的下腔高度。血液静电泵的设计中，下腔压力与输入、输出动、静脉压力相等，也就是说，其间压力差几乎为零[1]。

现将这些要点应用于其碟型阀门设计中。碟型阀门可保证流量随开角增大能迅速达到最大7.8cm3/s。此外，动、静脉压力又不能变，而阀门开启后需有要压力差来推动血液运行。为使下腔压力变化小，而使血液静电泵的设计改动尽可能小，其间压力差选择为0.005N/cm2～0.03N/cm2，小于主静脉压力 0.053N/cm2[1]，这是对本设计的要求。

因为流量系数α和雷诺系数密切相关，需要由碟阀不同角度开启后计算其中流速，再计算出雷诺系数，去核对相关的流量系数，以证明所选的流量系数的合理性，这能保证碟阀门管道血流畅通无阻，最终得到合适的碟阀半径r0是本文碟型阀门的设计目的所在。

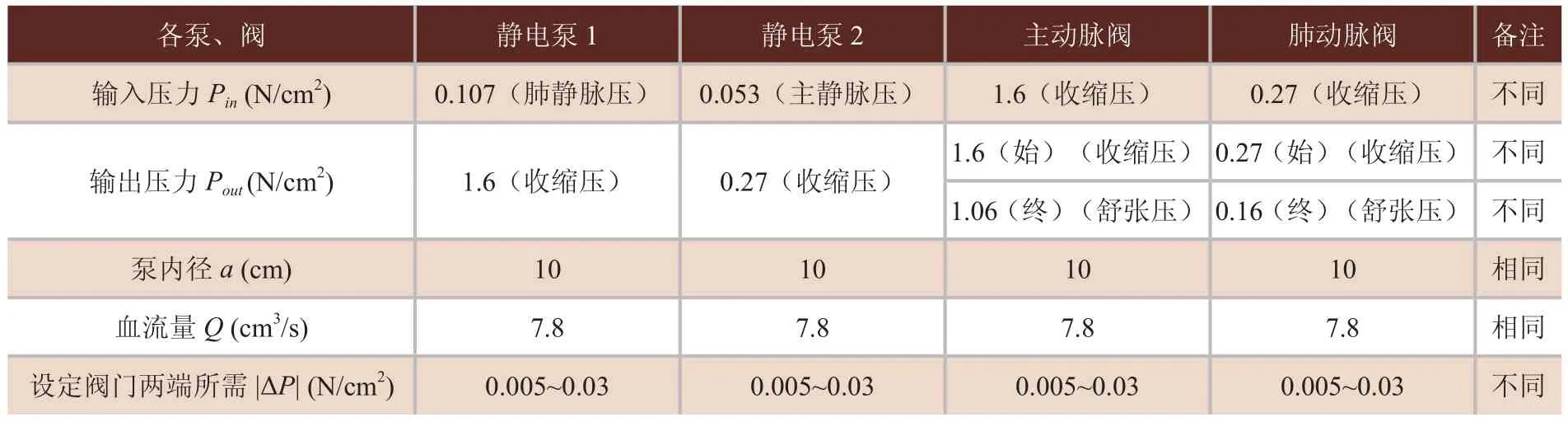
表1 主动脉和肺动脉静电泵、阀的各参量值[1]

此外，本文还研究了因阀门的快启导致血流冲击碟阀上所产生的撞击力，又进行了碟阀及其把柄的强度核验。

三、碟阀型阀门工作原理及设计

1、基本要求

本文是为血液静电泵的阀门设计的。入出血液碟型阀门设计的基本要求和球型阀门设计相同，详细内容可参考文献[2-5]。

由于出入管与主动脉和肺动脉相联接，因此，其输入PBin、输出PBout是人体固定压力[1]不可改变，如表1所示。可以更改的是出、入血状态时的血液静电泵下腔压力PBchu和Pru。但是，血液静电泵是已设计完毕的，而且按照输入时Pru=PBin和输出时PBchu=PBout设计的[1]，如果PBchuBB、Pru变动太大，则血液静电泵的静电激励电压和上腔压力变动太大。为此，ΔPB=Pru-PBinB和ΔP=PBchuB-PBoutB尽量减小，比如ΔP=0.005N/cm2～0.03N/cm2。

因为各血液静电泵、阀的流量Q全相同，为7.8cm3/s不能改变，因此，输出阀和输入阀的设计就在于保证所规定的流量Q和压力损失ΔP的条件下，选择碟阀合适的开角和阀套大小，并小于静电泵下腔高度，以减小纵向高度。从下文的结果来看（图4），r0＞0.2cm～0.35cm能保证血流畅通无阻。

2、流体力学关系

图1所示为入出血液碟型阀门结构示意图。

对于任何流通面积为A的管道，考虑到流体受到碟阀的阻力（图1），实际的流量为[6]：

其中，Q —体积流量；

A —碟型阀门套流通面积；

ΔP —碟型阀门前、后一定距离处的流体的压力差，也称为压头损失，对于阀门套管道，流量是指流入和流出的正向，故下文ΔP中就只取其绝对值进行讨论；

ρ—流体的密度，当流体为血液时，ρ=1.05g/cm[7]；

α —流量系数，它与碟阀的开口角度、壁面光洁度、血的粘度、雷诺系数有关，α＜1。一般来说，雷诺系数超过一定大小后，流量系数不再增加，达到最大值 αmax=0.7。

考虑量纲的变换，则由式（1）可得流量与压力及阀门套半径r0的关系为：

其中，压力ΔP单位为N/cm2，流量Q单位为cm3/s，r0单位为cm。

3、碟阀中流量计算常用方法

根据文献[6]，碟型阀门流量Q与碟阀开角θ的相对关系为指数关系，即：

其中，Q —阀门流量；

θ —碟阀开角；

R —相对流量，为最大流量与最小流量之比，R=Qmax/Qmin。

由于碟阀上无控制机构，所以碟阀不能随意停止在某一开角上，阀门流量与碟阀开角的相对关系仅有理论价值[1]。

对于碟型阀门来说，阀门处于最大可开启角时有最大流量，关闭时最小流量为零。当Qmax=7.8cm3/s，碟阀关闭 θ=0时，如选 R=10，Qmin≈ 0.78cm3/s，又选R=200，Qmin≈ 0.034cm3/s，再选 R=2000，Qmin= Qmax=0.0039cm3/s ≈ 0，可见R=2000，θ=0时，Q几乎为零，碟阀就关闭严密。如果选R=10，碟阀关闭不严。

对于本设计的碟阀来说，取R=2000，由式（4）有：

碟阀全开启时，θ=θmax=7π/16（由于阀把柄的转角可能达不到π/2），各血液静电泵、阀的阀门流量全部为Qmax=7.8cm3/s，由式（4）得到如图2所示Q与θ、R的关系。

4、碟阀中流量系数α与开角θ的关系

从式（2）可看出，流量Q与流量系数α成正比。对于碟阀来说，流量Q与其开角θ成指数关系，如式（4）。因此，α与θ也应严格成指数关系。

利用式（2）、式（4），在R=2000压力差、阀门管道面积不变的条件下，可以建立流量系数与开角的指数关系为：

其中，α —流量系数。

由式（4）、式（6）可以得到阀门实际流量与碟阀开角、压力差、阀门管道面积的关系，并设计出碟阀阀套的恰当的最小半径。式（4）、式（6）两种指数关系形状一致，差别仅在于标度不同，这是本文的特色。

当 θ=θmax≈7π/16，αmax=0.7，由式（6）有：

这就是α与碟阀的开角θ的关系，如图3所示。

当 θ=0 时，则由式（7）有：αmin=0.7×2000-1≈ 0

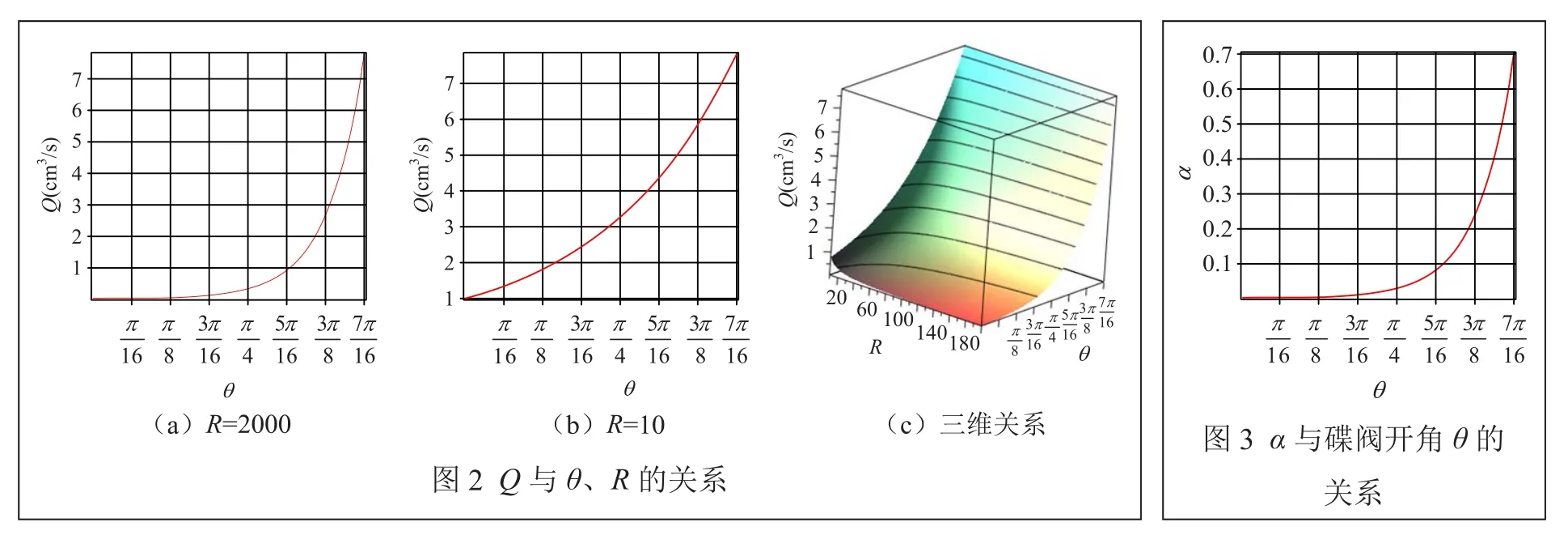
图2和图3曲线都是指数曲线，差别在于纵坐标标度不同。这一曲线的适用条件是θmax≈7π/16时，Q=Qmax，又αmax=0.7。对于其它开角θ，式（7）也成立。

5、碟阀中Q与r0、ΔP、θ确切关系

因为式（5）是碟阀开角不同θ时的相对流量，看不出与r0、ΔP的直接关系。但真正的实际流量还与管道条件r0、ΔP、α有关，即与θ、r0、ΔP有关。由式（2）、式（5）、式（7）可得阀套管道的半径公式为：

图4示出r0与ΔP、θ的关系。Qmax=7.8cm3/s是碟阀开口最大θmax=7π/16时的最大流量，因此，图中θ在7π/16附近时，即为Qmax=7.8cm3/s时最小r0与ΔP的关系。其中横坐标ΔP=0.005N/cm3～0.03N/cm3，取值小的原因是为使各泵基本已设计好的下腔压力不改动太大。r0min=0.22cm～0.34cm，是所有泵、阀应选择的一致最小半径，可大不能小。选择所有泵、阀的一致最小半径的合理性还要视下节雷诺系数和流量系数的核对结果。

6、雷诺系数和流量系数的核对

流体流动状态由流速、管道半径、粘滞性所决定，这几个因素综合在一起得出[5][7]：

其中，Re —雷诺系数；

ρ —流体的密度；

v —流体的流速；

l —流体流过的管道特征线度；

η —流体的黏度系数。

当流体流过圆形管道时，l为管道半径r0，v=QV/A，血液的 ρ=1.05g/cm3[9]，η=5～10×10-2g/cm·s（1 0 ℃）[10-11]。

雷诺系数可取下式：

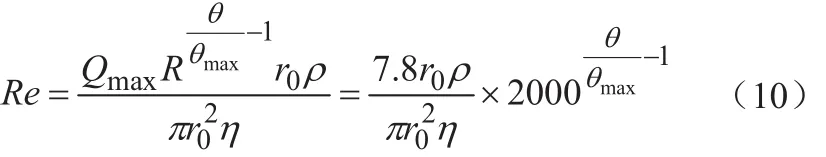
图5示出Re与r0、θ的关系。由图5可见，r0一定时，θ越小，雷诺系数Re越小。θ = θmax= 7π/16时，雷诺系数Re最大。阀套管道的半径r0越小，流速越大反而雷诺系数Re越大。因为本文讨论血液静电泵的阀门设计，阀门只有完全关闭θ=0和完全开启θ=θmax=7π/16状态。雷诺系数Re与开角θ关系只有理论讨论意义，所以图5只需示出θ=θmax=7π/16时，雷诺系数Re与阀套管道的半径r0的关系。对于各种管道来说，αmax代表最小阻力，一定ΔP下此时流量最大，也就是说雷诺系数尽可能大为好。但是阀套管道的半径r0过小，一定ΔP下达不到阀门能控制的最大流量，相当于增加了阻力，使流量系数α减小。

由图6可见，阀套管道的半径r0宜取0.2cm～0.5cm为佳。此时雷诺系数Re为120～50，由下文可见，流量系数可达到α=0.7，而且与ΔP无关。r0=0.2cm～0.5cm时，由图4可见，ΔP=0.03N/cm2～0.005N/cm2，满足尽可能小的压力差的要求。

根据苏锋等[8]对浮子流量计 研 究，α≈0.26～0.7， 取 值大小与雷诺系数有关。对水来说，ρ=1g/cm3，η=1.3×10-2g/cm·s（10℃），雷诺系数从1.1到16增大10倍多，而α从0.26按根号式增大趋近于常值0.7。血液的粘度 为 η=10×10-2g/cm·s[10-11]， 那 么Re＞＞2后，α增大趋近于常值0.7。也就是说，阀套管道的半径r0=0.2cm～0.5cm时，雷诺系数Re＞＞2，流量系数可达到α=0.7，而且与ΔP无关。

四、碟阀受力计算

1、冲击力与流量关系

全面积A冲击力作用于碟阀中心上，表达式为：

其中，Q —全面积流量，单位：cm3/s；

Ft—作用于碟阀中心上的力，单位：Dyn，除以105后为N；

ρ —血液的密度，单位：g/cm3；

A —阀门套管道的面积，单位：cm2。

对于独立血液静电泵已将最大流量定为7.8cm3/s，阀门打开时，血流应全部流出。这是指每秒一次心博的泵血量。实际仅在心肌收缩，即血液静电泵的激励由最大变最小时才泵血，这一时间仅为一个心动周期约1/5s[1]，因此，阀门套管道中最大流量为Qmax=39cm3/s，持续1/5s，但这不影响前面的讨论。

2、在碟阀打开θ角时的冲击力

当碟阀开角θ=θmax时，阀门套管道中流量Qmax=39cm3/s，全面积冲击力作用于碟阀中心上，沿管道π/2方向，已知血液ρ=1.05g/cm3，则由式（11）得：

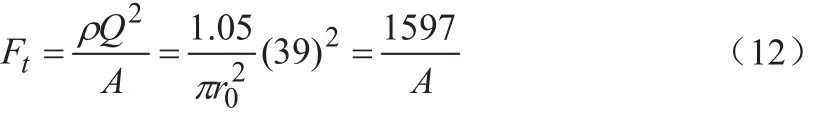
当碟阀打开角为θ时，如图7所示，阀门套管道的全面积冲击力作用于碟阀中心，沿管道π/2方向，表达式为：

F1分解为碟阀的垂向力F2和沿碟阀的平行力F3：

F2在碟阀上产生转矩（r0+0.2cm为F2离轴心距离0.2cm，取值考虑把柄长≈r0，太短，胶块离阀心也短，阀门开不大，血流受阻）与碟阀把柄上的反转矩相平衡（如图7所示），表达式为：

反转矩由胶块的沿碟面的垂向反弹力F4所产生，设胶块离轴心0.1cm（0.1cm取值比柄长小，太长胶块离阀心短，阀门开不大，血流受阻，而且柄糟太深）则有：

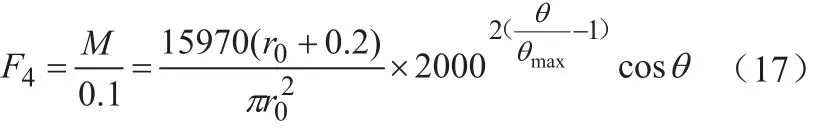
将胶块设为支点，支点上的弯矩为：

其中，(r0+0.1)为F2离开支点的距离（M1未在图7中示出）。可见F4较大，需要由F2和轴心上的沿碟面的垂向力F5来平衡：

图7中的F6用来平衡F3，大小相等，方向相反：

由于有胶块的沿碟面的垂向反弹力F4存在，它能托住碟阀，则F2在碟阀上可产生压力：

图8示出碟阀圆面上F1、F2、F3、F4、M1、ΔP（图中的纵坐标）与r0、θ的关系，其中，已将所有力单位Dyn转化为N。在相同θ下，F5是F4的0.9倍，M是M1的倍，不再示出。由图8(e)可知，碟阀把柄支点上弯矩M1与其半径和开角θ有关，θmax时最大。

3、应力分析

（1）碟阀打开θmax角时圆形碟阀把柄的截面上平行向应力

设碟阀把柄的高度为圆形碟阀厚度的一半，h=0.1cm，宽度W=0.1cm，圆形碟阀把柄支点上的弯矩为M1。圆形碟阀把柄的支点上截面上垂向应力为σ⊥。σ⊥与 M1有关[12]：

其中，x —轴套上所考虑点离开把柄中线的坐标±距离。当x=h=0.1cm、W=0.1cm时，有：σ⊥=12000M1(N/cm2)

把柄的截面上沿碟阀面均匀应力为：

当h=0.1cm，W=0.1cm时， 有：σ∥=100F3(N/cm2)

图9示出了圆形碟阀把柄的截面上平行向应力σ⊥和σ∥与r0及θ的关系。

图9（a）示出把柄支点的截面上下外表面垂向应力σ⊥与圆形碟阀半径r0及开角θ的关系。可见，θmax= 7π/16，r0=0.2cm 时，σ⊥=90N/cm2。

图9（b）示出把柄的截面上沿碟阀面均匀应力σ∥与圆形碟阀半径r0及开角θ的关系。在r0=0.2cm时，把柄的截面上外表面两应力叠加结果可达102N/cm2。所以这里是薄弱处，但是，仍远未达到钛的屈服极限。

（2）碟阀打开θmax角时圆形碟阀面上的径向应力

由图8（f）可知，碟阀上压力ΔP与r0和θ有关，θmax时最大。设碟阀厚为h，圆形碟阀边缘的最大径向应力的理论公式为[12]：其中，ΔP分别对应图8（f）中r0=0.2cm时的ΔP=0.19 N/cm2，r0=0.5cm 时的 ΔP=0.005N/cm2。

图10示出了圆形碟阀边缘的最大径向应力σrr与圆形碟阀半径r0及厚度h的关系。当圆形碟阀厚度h=0.2cm时，圆形碟阀边缘的最大径向应力σrr分别为0.14N/cm2和 0.025N/cm2。

（3）在碟阀关闭时的应力分析

在碟阀关闭时的压力为ΔP=0.005N/cm2～0.03N/cm2，碟阀厚为h=0.2cm，圆形碟阀边缘的最大径向应力的理论公式如式（24）[12]。

图11示出了圆形碟阀边缘的最大径向应力σrr与圆形碟阀半径r0及压力ΔP的关系。对应r0=0.2cm、0.5cm。圆形碟阀厚度h=0.2cm时，圆形碟阀边缘的最大径向应力分别为σrr=0.025N/cm2、0.14N/cm2。

（4）应力分析总结

碟阀把柄的截面上应力σ⊥与沿碟阀面均匀应力σ∥的叠加结果，以及圆形碟阀边缘的最大径向应力σrr均未达到钛的屈服极限8.272×107N/cm2[13]。

五、小结

1、因为本文为血液静电泵的阀门设计，它由10个独立静电泵并联而成，每一个流量Q=7.8cm3/s。血液静电泵已设计完毕，为使血液静电泵的静电激励电压变动不大，为此，设ΔP=0.005N/cm2～0.03N/cm2。血液静电泵只有开和关两态，由静电激励自动控制，阀门的碟阀随之动作，故碟阀的转轴只能设计在一侧。

3、一定ΔP下为达到阀门能控制的最大流量，阀套管道的半径r0宜取0.2cm～0.5cm为佳。此时雷诺系数 Re＞＞2，流量系数可达到 α=0.7，ΔP=0.03N/cm2～0.005N/cm2，满足尽可能小的压力差的要求。

4、实际仅在心肌收缩，即血液静电泵的激励由最大变最小时才泵血，相当于管道中最大流量为Qmax=7.8×5=39cm3/s，持续1/5s。当碟阀打开角为θ时，阀门套管道的全面积冲击力为，可达0.02N～0.12N，与碟阀半径r0有关。由该力可计算出在碟阀的垂直和碟面的平行分量及弯矩。再计算各力引起的诸应力，可达0.02N/cm2～21N/cm2。这与碟阀r0、厚度、把柄的长度和截面尺寸、胶块支点位置有关。碟阀把柄的截面上平行向应力σ⊥和σ∥叠加结果可达102N/cm2。圆形碟阀边缘的最大径向应力与厚度及半径有关，h=0.2cm时，圆形碟阀边缘的最大径向应力＜1N/cm2。