荧光衰减型光纤测温
杨和平 朱杨凯 周正超 谢志迅 谢志行
1. 南京大学,江苏南京 210023;
2. 南京力通达电气技术有限公司,江苏南京 210000;
3.南京大学金陵学院,江苏南京 210089
一、引言
当今世界,对于机器自动探测的研究已经处于较为深入的状态,并开始对探测数据的精确度和抗干扰能力,以及对环境的自适应性能力进行探索。其中,光电信号的充分运用对工业生产和日常生活中的技术和速度提升有较大的影响,光纤传感技术对于当今时代十分的适用,信息传感技术的发展也将会是现在以及未来的一种趋势。在21世纪,光纤传感技术更是传感领域中研究与开发最为活跃的技术,由于光纤的许多自身的物理性优点,因此,在高直流电场、高频领域、微波场等极端的环境中的应用十分普遍[1]。
现有的荧光光纤测温系统的光学组件部分相对复杂,而且集成不高,这增加了相应的体积和成本,同时光路的抖动也会影响测温的准确性。光纤一端与光路耦合的部分大都采用直接对光,这样耦合效率较低,而且光纤很难固定,并且荧光端在进行封装的时候,一般只是在端部包裹一层保护套,这种方式使得测温探头无法很好的与被测物体对接,不利于进行热传递,使得光纤温度传感器的测量效果较差,因此,本文通过实验数据采集和数据分析进行一种工业上简易适用的荧光传感探头,并提出一种拟合算法对该荧光温度传感器进行测试,通过示波器对荧光粉的温度差异性进行测试,从而选出作为传感器荧光物质材料的最佳材料。本文的主要工作有:
(1)在理论研究方面,通过查阅文献对荧光光纤传感技术的理论和应用问题进行了较为全面而系统的阐述,提出了基于荧光强度信号测量的荧光光纤温度计的研究目标与实施方案,并分析了温度计的光路结构,对荧光光纤温度计的光纤传感探头进行了工业化的设计;
(2)进行了紫外光源与荧光传感材料的一致性实验;
(3)优化了测温探头,并提出对光电模块的改进方案;
(4)在嵌入式平台中实现最小二乘的拟合法,提高拟合曲线的精确度,实现算法计算参数。
二、基本测量原理
荧光发光原理是荧光衰减型测温系统实现的根本理论基础,这是一种光致发光的现象,其重要的理论支撑为:当荧光材料在可以激发它产生荧光的特定光谱波段的光照射后,会产生超出热辐射的发光现象,而对于这种激发不光是光激发,也可以是某种形式的电磁辐射的影响,然后在这种激发的激励停止之后,荧光受激发的这种发光现象将会持续一段时间才会消失,并且根据这种持续的时间,我们可以根据时间的长度分为长衰减型和短周期型,也称为磷光和荧光的区别[2]。
荧光的产生在材料学中原理是电子在不同能级之间的跃迁产生的持续发光现象,具体原理如下:电子在高能级被激发后向低能级跃迁发出能量,这种能量以特定的形式向外发散,如光、热等,而荧光衰减现象则是由于这种跃迁的持续能力。通常荧光材料的电子跃迁时间量级在ms级。一般来说,我们将这种能够发出持续衰减的荧光的物质成为荧光材料。
与普朗克定律相一致的是,当一种物质在进行能级跃迁之后,波长为r的光波会在这一过程中发射出,在激发光消失之后,激发态的荧光寿命会决定这种荧光衰减的持续时间,这种持续时间也被称为是荧光受激发之后的衰减寿命[3]。对于荧光的衰减来说,大量的科学实验发现,衰减的光强随时间的变化曲线型类似于指数型的函数。在大量的数据采集和描绘曲线后,衰减时间和光强之间确实存在一种指数函数的关系。针对这种函数关系,我们可以计算和拟合出对应的曲线函数和特征参数,其中,特征参数也被称为衰减曲线的衰减特征值。根据理论上来讲,一般满足温度的正相关关系,在所有荧光物质发光的过程中,由于辐射或者是非辐射竞争的存在会产生一些延迟效应,这种外在因素会导致激发态寿命的缩短,因而,我们在针对不同的应用时要关注不同的温度需求,并对应的采取不同的荧光材料和相应的保护措施。
荧光测温就是根据这种温度相关性来进行的,针对这种温度相关能力,通过对荧光信号的转换检测转化的电信号,描绘出荧光衰减的指数型衰减曲线与温度之间进行匹配拟合。
本论文中采用的是荧光寿命衰减型,即通过对荧光返回的衰减的曲线与温度之间的关系测量温度。用窄带脉冲激发光对荧光材料进行激发,荧光材料发光,并形成激发态荧光体,这种形态的光强会随着时间产生衰减,其衰变率为:

其中,N0—荧光光强的峰值常量;
t —时间系数;
τ —对应荧光材料的衰减系数。对于以指数形式衰变的荧光物质,其发射强度F(t)和激发态分子的数量N(t)成正比,即:

其中,F0—ϑ N0之后的常数值;
t —时间系数;
τ —对应荧光材料的衰减系数。
对这两个参数函数应对时间作图,可得如图1所示曲线[4]。荧光寿命也就是从最高峰值的光强衰减到0时的时间参数,lgF(t)对时间t的曲线斜率为荧光寿命倒数的负值τ-1。而事实上,在荧光物质受到激发之后,一些受激发的分子会立即返回原来的基态,有一些甚至会5倍的延迟后,荧光寿命结束返回基态,这就会导致实验确定的荧光强度的衰减曲线。

在实验表明下,不同环境温度荧光寿命不同,荧光衰减曲线的参数可以与温度呈现一定的关系:

其中,RE、Rf、ΔE、k —常数;
T —绝对温度。

表1 待测荧光粉测试数据
因此,通过这种方法可以测量环境温度,且对光强进行精确测量,荧光材料的选择以及光源波段的选择显得尤为重要,温度的参数变量仅由“荧光寿命”的特征参数决定,该特征参数不会受到光源的波动影响,降低了对控制光源稳定的严格要求。对比其他的荧光温度传感器简化了结构,降低了成本,提高了性能,同时可以通过算法的方式对结果进行进一步提高精度。
三、探头制备及实验采集
首先,光纤探头是实现光纤测温的基础,为了在采样过程中减小误差,则由光电探测器转换的荧光衰减电信号要满足以下几个条件:幅度上易于区分、衰减时间大于1ms(芯片采样可以达到1μs一次)、荧光的中心波长与光源有区分(利于二相分色镜的分光)。因此,我们选取了几种较为典型的荧光粉进行测试,并选取对可以激发荧光且中心波长在406.5nm的紫色光源。通过Morpho光谱仪进行分析荧光光谱的特性,实验数据如表1所示[5]。
由实验数据选取了效果较好的3、4两种荧光粉进一步测试,发现在镀上光纤端头之后满足技术要求,图2为光谱仪测试3、4两种激发后的效果。
制作光纤端头时,将选定的红色波长的荧光粉溶于特定浓度比的透明环氧树脂溶剂中,充分搅拌并在显微镜下观察分布是否均匀,取少许粘在切割好的断面处,保持光纤竖直让荧光粉完整覆盖在端面上,形成半弧面的形状,然后等待环氧树脂凝固(选取的为单向凝固的环氧树脂),等完全凝固后可以对端头进行二次操作,安装相应的热传导能力强的保护层,保护层要注意运用导热性较好的材料,具体的安装要看端头测量的环境,应该相应的安装保护层[7]。具体的效果如图3。


对于测温系统的整体搭建图如图4所示[6]。先通过示波器手动测量数据,用软件进行曲线拟合,计算出各种温度下的衰减参数,再进行数据分析。
另外,本论文中对传感器探测的光电模块中包括光源发射器、耦合器、1mm塑料光纤、光电转换器、荧光探头以及光电探测回路。紫色LED光源通过分光镜经过耦合器进入光纤,在耦合器端口要注意光纤的ST头与117A模块的耦合度,光源通过光纤打到荧光传感端头上面,荧光信号通过光纤返回到模块中,经过分光镜,从另一路照在光电探测器上,从而将衰减的荧光光信号转换为电信号,通过模块的芯片多次在不同的时刻采样,分光结构如图,具体光路系统如图5所示。
四、算法拟合实现
最小二乘法(也称为最小平方法)是一种数学优化数据的计算方法,采取寻找最小化的平方和获取数据的最有函数匹配的数学方法。最小二乘法相当于一次插值计算,可以寻找到未知数据,并使得最小化所获得的数据和实际数据之间的误差平方和,进一步模拟出拟合多项式的系数参数,生成对应的数据集合,数据点集合{(Xi,yi)}(i=0, 1, 2,…, m),在取定的函数类φ中,求p(X)∈φ,使误差的平方和E2最小:
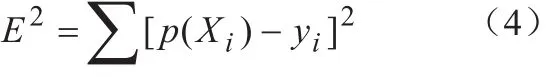
从几何的角度来讲,要找到寻求与给定点集{(Xi, yi)}(i=0, 1, 2,…, m)的距离平方和为最小的曲线y=p(x)。函数p(x)称为拟合函数或最小二乘解结果,求拟合函数p(x)的方法称为曲线拟合的最小二乘法[7]。
原理:根据MATLAB中的polyfit(x, y, n)函数执行多项式曲线拟合的方式,其中,n为拟合的多项式次数,设拟合多项式为:y=a0+a1x+…+akxk,各点到这条曲线的距离和,也就是偏差平方和如下:

为了求得符合条件的a值,对等式右边求偏导数,故而我们得到:


由式(6)化简得到:通过以矩阵的形式表示这些方程,就可以得到下面的矩阵:

将这个范德蒙矩阵化简后可得到:

也就是说X*A=Y,那么A=(X'*X)-1*X'*Y,通过矩阵计算便得到了系数矩阵A,同时,我们也就得到了拟合曲线的相关具体参数。
五、数据采集及分析
为了对衰减曲线与温度之间的关系进行研究,对光电传感和输出衰减信号,用示波器进行人工数据测量,并计算对应的曲线衰减参数。
具体的操作如下:用驱动电路对模块进行驱动,用分频设计确定好激励脉冲的频率和脉宽,使紫色LED发出脉冲光,对荧光材料进行激发,再由示波器测量光电探测器的输出的衰减电信号的曲线。对于上文中效果较好的荧光粉材料对与不同温度下的衰减曲线进行取点测试,固定的横坐标分别为5.0, 7.5, 10,12.5, 15, 22.4(ms),测量数据如表2、3、4所示,由于示波器测量的精度不高,无法满足实验的0.1%的要求,因此在多次测量后,选取660nm长衰减型荧光粉对不同温度下的测试数据进行曲线拟合,并通过取对数运算得到曲线的衰减系数,在MATLAB中对温度与衰减系数进行线性匹配。

表2 660nm红色荧光粉温度测试

表3 650nm红色荧光粉温度测试
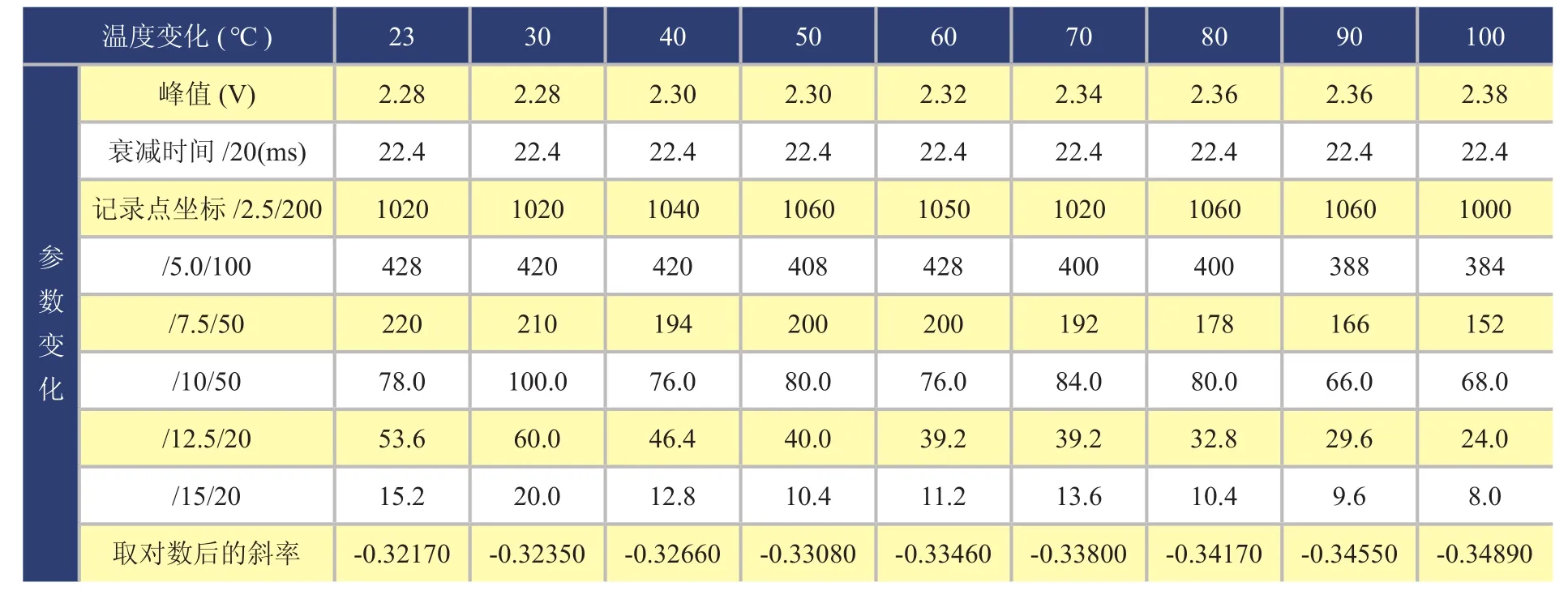
表4 660nm长衰减型荧光粉温度测试
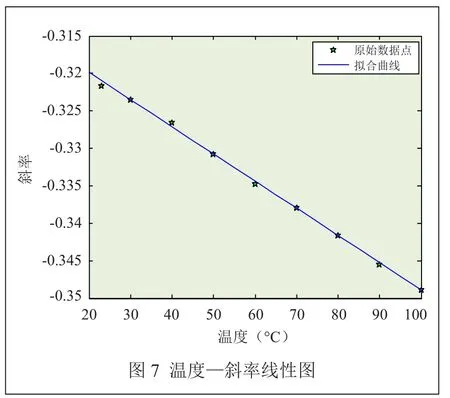
经过多次示波器手动测量数据,对数据进行处理得到衰减的参数——对数斜率,根据已知原理,观察是否具有线性特征,用MATLAB进行处理数据,将拟合曲线与采样点在一张图中展现,如图6所示。观察曲线拟合的优劣,在通过两边同时取对数,使变成线性,再通过最小二乘法算法拟合出最佳线性,得到斜率,并通过图像来展示(图7),由于手动操作示波器的误差较大,以及采样的温度点太少,线性效果与预想相差较大,在通过基于STM32F407多次延时采样得到数值,再经过以上一系列操作后发现线性效果明显。另外,猜想是由于模块本身具有基态不稳定的噪声信号,需要对基态信号的一些数据进行滤除。

六、总结
通过实验表明:荧光衰减型光纤测温对于温度变化具有良好的应变性,且精度较高,在工业电力设备中运用相比较于其他设备,结构更加简单,成本更低,性能及抗干扰能力更强,最重要在于精度较高[8]。相对于目前较为成熟的测温系统如膨胀式测温系统和红外热成像系统,它们的测量误差大,并且红外热成像只能测量表面温度。故而,这种荧光衰减型光纤测温体系从传感探头的简易度和执行性,到拟合算法的效率相较于现在市场上的测温方式更加优越。荧光衰减型光纤测温系统的实现,在与传统的测温方式的对比之下显得尤为适合时下日益发展的电力行业的监测需求,它具有抗电磁干扰、精确度高等十分显著的特质,而且其成本和低维护的商业价值也有重要的推广价值。