基于最小二乘法的雷暴天气下飞行改航决策研究
何光勤,鲁 力,胡敬玉,马 昕
(中国民用航空飞行学院空中交通管理学院,四川 广汉 618300)
飞机在雷暴天气中飞行是十分危险的,不仅会产生严重颠簸影响旅客的舒适度,还有可能受到雷击以及积冰和冰雹的影响,对飞机电子设备和结构安全造成巨大的威胁[1]。1994年2月4日,美国一家航空公司的DC-9-31飞机在飞行中进入雷暴区时,两台发动机吸入大量水和冰雹,发动机压缩器损伤导致失速坠毁。因此,预测雷暴的位置,有效避免飞机飞行中受到雷暴天气的影响有着重要意义。早在1842年,奥地利物理学家J.Doppler从运动声源受到启发得出多普勒效应,根据此效应研发的多普勒气象雷达对民航业的运行安全发挥了重要作用,它通过发射高频脉冲电磁波信号探测搜索范围内的气象情况,比如湍流、雷暴等天气,再根据反射信号的频差、相位差、衰减等特性分析前方是何种天气状况,并用不同的颜色反映到雷达回波图上[2]。近些年,国内很多学者根据气象雷达回波图,采用最小二乘法进行了雷暴走势预测,如陈岚峰等[3]采用Matlab软件对曲线进行了最小二乘法拟合仿真研究;梁平等[4]运用最小二乘法和地理加权模型对汉江流域土地利用类型与水质关系进行了评估;肖云等[5]利用空域最小二乘法分析了重力卫星误差;陈晓倩等[6]采用最小二乘法预测了无人机路径。对于航空器碰撞风险,国内一些学者对此也做了一些研究,如吕宗平等[7]采用CREAM和IDAC模型对航空器碰撞风险进行了评估;薛宇敬阳等[8]采用飞行路径算法预测判断了飞机碰撞风险。另外,还有一些学者采用各种算法模型对民航事故征候进行了分析和预测[9-14]。
基于上述研究,本文基于气象雷达回波图分析,采用最小二乘法进行了雷暴走势预测,并判断飞机正常飞行是否会受到雷暴天气的影响,若受影响飞机则需要改变原飞行航迹,以避免穿越雷暴区而引发的严重事故。
1 理论与算法
本文利用两运动物体相撞模型,判断飞机沿预计飞行航迹运动是否会在未来某时刻受雷暴天气的影响。对于飞机的运动,知道运动速度和航向,可计算飞机运动的轨迹方程。但对于雷暴的运动,运动方向和速度在不断的变化,需借助软件找到雷暴运动的轨迹方程。
1. 1 飞机运动的轨迹方程
物体运动轨迹在二维坐标系中可分解到x轴和y轴上,用x(t)和y(t)表示物体相对两坐标轴关于时间t的运动方程。飞机沿预计飞行航迹的运动速度和航向是已知的,可找到飞机运动的轨迹方程,记为x0(t)和y0(t)。
1. 2 采用最小二乘法拟合雷暴运动的轨迹方程
在气象雷达回波图中,雷暴颜色越浓(见图1),雷暴等级越大。CAD软件具有分析图像以及准确、方便地找出坐标数据的功能。因此,利用气象雷达回波图得到的某时刻雷暴的坐标数据[15-16],并采用最小二乘法可拟合得到雷暴运动的轨迹方程x′(t)和y′(t)。

图1 气象雷达回波图Fig.1 Meteorological radar echo map

(1)
其中,x′(ti)可以是ti的一次、二次或三次方程,由Q对参数求导等于0即可得到Q的最小值,则x′(ti)则可由参数a、b、c表达。
本文选取多个方程,但找出最符合雷暴运动的轨迹方程则需要进行方差分析。假设在未来t时刻已知雷暴的坐标数据为(x0,y0),再利用Matlab软件拟合得到的雷暴运动轨迹方程计算在t时刻雷暴的坐标x′(t)和y′(t),其方差计算公式如下:
D=(x′(t)-x0)2+(y′(t)-y0)2
(2)
找出方差最小的方程即为最匹配雷暴运动的轨迹方程。
1. 3 两运动物体相撞判断
将飞机和雷暴当成两运动物体,由于两物体的运动轨迹均可视为沿x、y轴运动相对于时间t的函数方程,则两运动物体之间的距离可写成关于时间t的函数,即:
(3)
S对t求导可得极值,由此可得出在未来何时两物体间的距离最小,并将其最小距离与飞机运行标准相比,若该最小距离小于飞机运行标准的要求,则飞机需要提前改变飞行航迹以避免飞机与雷暴相遇。
2 方法与验证
2. 1 方法分析过程
本文以2018年6月9日首都航空JD5690次航班经由宜昌三峡机场飞往杭州萧山机场的飞行过程为例,根据气象雷达回波图可知当日在此航班飞行航路上有雷暴天气,利用两物体运动相撞模型,评估飞机在终端区若沿预计飞行航迹运动是否会受雷暴天气的影响。本文基于气象雷达回波图分析,并采用最小二乘法进行雷暴走势预测,该方法的具体分析过程如下:
第一步:找出飞机运动的轨迹方程。
首先,根据飞机的运动速度和航向,以及气象雷达回波图并结合Auto CAD软件,可获取JD5690次航班不同时刻在气象雷达回波图上的坐标位置,见图2。
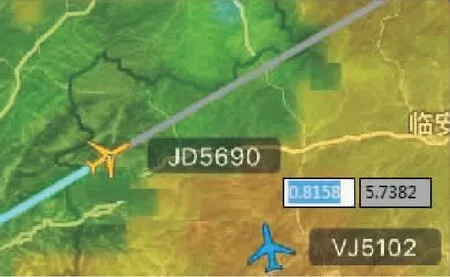
图2 JD5690次航班不同时刻在气象雷达回波图上的 坐标位置Fig.2 Coordinate position of flight JD5690 on the meteorological radar echo wave at different times
本节给出的飞机运动轨迹坐标值的比例尺均为1∶25 000,单位为m。
然后,根据飞机在17∶00 pm和17∶04 pm时刻的坐标位置分别为(0.821 7,5.733 8)、(2.036 3,6.401 8),可得到飞机运动的轨迹方程为
(4)
最后,使用Matlab软件作出方程(4)的曲线,即飞机沿预计飞行航线运动的轨迹图,见图3。
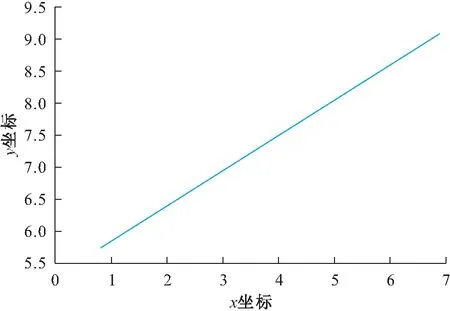
图3 飞机沿预计飞行航线运动的轨迹图Fig.3 Trajectory map of the aircraft along the expected track movement
第二步:找出雷暴运动的轨迹方程。
雷暴的运动速度和方向都是时刻变化的,首先根据气象雷达回波图并使用Auto CAD软件,找出已知时刻雷暴中心的坐标位置,见表1。

表1 已知时刻雷暴中心的坐标位置数据列表
然后,利用最小二乘法并使用Matlab软件,找出符合已知条件的雷暴运动轨迹拟合方程如下:
(5)
(6)
(7)
第三步:根据方差找出最匹配雷暴运动轨迹的拟合方程。
采取16∶31pm时刻实际雷暴中心的坐标位置(4.345,7.751 8)和第二步中三个拟合方程[公式(5)、(6)、(7)]预测得到的在该时刻雷暴中心坐标位置的方差进行分析,并判断哪个方程的拟合效果最佳[17]。设三个拟合方程的方差计算结果为D1、D2、D3,则三个拟合方程的方差值见表2。

表2 三个拟合方程的方差值列表
由表2可知,拟合方程(5)的方差值最小,故选取该方程作为雷暴运动的轨迹方程,并使用Matlab软件作出拟合方程(5)的曲线,即雷暴运动的轨迹图,见图4。

图4 雷暴运动的轨迹图Fig.4 Motion trajectory map of thunderstorms
第四步:在规定的时间内计算飞机与雷暴之间的最小距离。
由两运动物体之间距离S(t)的计算公式(3),可计算未来20 min飞机与雷暴之间的最小距离。将飞机和雷暴运动的轨迹使用Matlab软件绘制到一张图中,由此可以直观地看出何时两者之间的距离最小,见图5。
由图5可见,大约在飞机运动轨迹的第8个轨迹点即约16 min时刻,飞机与雷暴之间的距离最小。
利用公式(3)具体求解过程中,应提前将飞机与雷暴运动的轨迹方程式在时间上相对应,再采用S(t)对t进行求导,即可求得在t0时的极小值S(t0),此步骤可在Matlab软件中编程求解,具体编程代码如下:
symst
x=@(t)(1.285 1*(10^(-4))*(t+113)^2+0.014 5*(t+113)+2.115 0-0.303 7*t-0.821 7)^2+((-3.828 4)*(10^(-5))*(t+113)^2+0.011 6*(t+113)+6.803 9-0.167*t-5.733 8)^2;<此代码表示飞机与雷暴之间的间隔>
[tmin]=fminbnd(x,0,20)
tmin=
15.900 4
[xtmin]=double(subs(x,t,[tmin]))
Matlab软件运行得出结果如下:
tmin
15.9004
xtmin=
0.746 9

图5 飞机和雷暴运动的轨迹图Fig.5 Motion trajectory map of the aircraft and thunderstorms注:点与点的时间间隔为2 min。
2. 2 利用数理统计学方法验证方法的可行性

本文运用数理统计学中的区间估计方法来验证该方法的可行性。首先利用中心极限定理可近视认为S(t0)服从N(μ,σ2)的正态分布,则μ=21,σ2=D(x)=0.070 4,而根据切比雪夫不等式:
(8)
然后根据飞机运行标准可知,飞机与雷暴之间的最小距离应当不低于25 km,而本文计算得到的飞机与雷暴之间的距离最小值为21 km,那么可设ε=4,使得在t0=15.9 min时刻飞机与雷暴之间的距离不大于25 km,计算得到其概率P≥0.996 5,即该事件为大概率事件,表明此方法是可行的。
相应地,t0为服从于N(μ,σ2)的正态分布,则μ=15.9,σ2=D(x)=0.070 4,在知道该时刻飞机与雷暴之间有最小距离21 km的前提下,给定置信水平为0.9,估计t0的置信区间,根据该置信区间可找出飞机需要改变飞行航迹的最早时间点,其置信区间为
(9)
由于预计雷暴运动轨迹方程使用的采样点有4个,故n=4,zα/2为标准正态分布的上分位点(见图6),经查表计算可得该置信区间为(15.842,15.958),则可视为飞机应在15.8 min时刻之前改变飞行航迹,以避免雷暴天气的影响[18-20]。
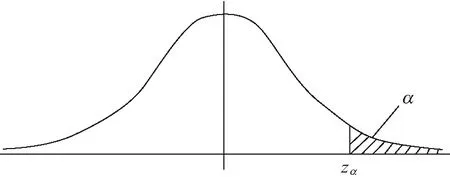
图6 标准正态分布上α分位点示意图Fig.6 Diagram of quantil on standard normal
根据第2.2节的区间估计方法,JD5690次航班已在10 min后改变了飞行航迹(见图7),这与本文利用最小二乘法推导出的结果基本一致。

图7 10 min后JD5690次航班改航图Fig.7 JD5690 flight diversion chart after 10min
2. 3 案例验证
2018年5月20号CA1860次航班由柳州飞往北京,本沿预计航路SJG飞往P59航路点,中途经过雷暴区(见图8,雷暴区颜色为红色),雷暴移动方向由西北方向向P59航路点移动。本文利用最小二乘法对雷暴运动的轨迹进行了预测,其预测结果如下。
雷暴中心在0 min (10) 飞机在0 min (11) 根据第2.2节的区间估计方法,可得出飞机预计在(1.982,2.342)区间与雷暴发生碰撞,因此飞机必须通过改变飞行航迹实行避让雷暴。如图8中的主飞行仪表(Primary Flight Display,PFD)所示,CA1860次航班的航向已改为280°,向西飞行,以避让雷暴,从而验证了本文提出的最小二乘法预测雷暴走势的准确性。 图8 CA1860次航班途经雷暴区Fig.8 CA1860 flight passing through the thunderstorm area 本文先基于气象雷达回波图并结合Auto CAD进行图像分析提取坐标位置数据,再采用最小二乘法进行线性拟合获得飞机和雷暴运动的轨迹方程,并通过两者运动轨迹方程的联立计算并判断飞机是否会进入雷暴区且受其影响,最后通过案例验证表明,实际结果处于最小二乘法预测的范围之内,说明该方法具有一定的准确性。本文在对雷暴运动的轨迹方程进行选取时运用了方差公式和切比雪夫不等式等数据统计学方法进行可行性分析,并采用置信区间评估飞机与雷暴之间最小距离时刻的时间容差,使该方法具有实际预测意义。但本研究在选取雷暴中心的坐标位置数据时有一定误差,且飞机在实际飞行中运动速度和航向也会发生变化,在以后的研究中,应对这些变化进行处理,使预测结果更加精确。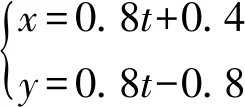

3 结 论

