排阵式交叉口交通安全分析及鲁棒优化模型
郑 喆, 马万经, 赵 靖
(1.同济大学 道路与交通工程教育部重点实验室, 上海 201804; 2.上海理工大学 管理学院, 上海 200093)
信号交叉口是城市交通道路网络的重要节点的“通行瓶颈”,对信号交叉口的优化设计及合理控制是提高其通行能力及保障运行安全的重要方法.传统的信号交叉口优化设计及控制管理主要是降低车均延误并提高通行能力,然而左转交通流及直行交通流的相互冲突仍是阻碍交叉口运行的重要因素.随着智能交通系统及相关技术的发展,一系列非常规信号交叉口[1-5]成为相关学者的主要研究方向,其中排阵式可较明显的缓解左转交通流与直行交通流的相互冲突问题,通过对上游车辆的预组织提高了进口道车道使用效率和交叉口的通行能力.
目前排阵式交叉口的相关研究主要为对其控制方法的可行性探究[6-8]、主预信号的协调控制[9-11]以及相关交通设施的设置方法[12-13]等,但对于排序区处交通运行安全的分析较少.此外,以往研究中普遍将排阵式交叉口预停车线处到达交通流视为均匀到达,对于实际应用中随机波动的到达交通流研究较少.因此,本文运用交通冲突技术[14-15]对排阵式交叉口排序区处交通安全进行分析,得到显著影响因素,并考虑进口道交通流量随机波动,运用多目标优化决策方法[16-17]建立鲁棒优化模型,然后运用主客观需求偏差最小法进行决策分析,从而得到排阵式交叉口最优鲁棒优化配时方案.
1 排阵式信号控制方法
排阵式交叉口是一种运用预信号控制思想的非常规信号交叉口.排阵式信号控制方法是在进口道停车线上游增设一条预停车线,并在预停车线处设置预信号灯,与主停车线处的主信号灯实行联动控制.排阵式交叉口的交通组织形式如图1所示,预停车线上游车辆在预信号处被重新组织并进入排序区,排序区内车辆按照主信号控制在相应相位驶离.由于排阵式信号控制的特殊方式,排序区内车道功能随信号周期不断变化,且同一相应排序区内所有车道的车道功能相同.由于特殊的交通运行特征,车辆在排阵式交叉口运行时较常规信号交叉口行驶较为复杂,因此排阵式交叉口的运行安全性是其通行效率及正常运行的基础和重要保证.

图1 排阵式交叉口交通组织形式
2 排阵式交叉口交通安全分析
2.1 交通冲突发生机理
排阵式信号交叉口与常规信号交叉口相比,增加了预停车线、预信号及排序区,使得交叉口的交通冲突分为以下4种类型,其产生机理如下:
(1) 左转车流冲突.设置排序区进口道的方向采用左转保护相位控制,但由于左转及直行车辆在所属相位均可使用排序区全部车道,当左转流量较大或对向直行流量过大且在直行绿灯末期仍持续进入交叉口时,排序区内多车道左转车辆同时运行,内侧左转车辆转弯半径过小,在汇入出口道会与外侧车道左转车辆存在一定冲突,进而与对向直行车辆形成交通冲突.
(2) 直行车流冲突.与左转交通流相似,当主信号直行相位阶段,排序区内直行车流通过交叉口,当直行流量过大时,在主信号直行相位绿灯末期离开排序区的直行车辆可能会与下一相位的车辆发生交通冲突.
(3) 预停车线处分流冲突.由于排序区的特殊设置,排序区内车道功能相同,致使直行车辆或左转车辆在预信号绿灯启亮后,需要从预停车线前的单车多或双车道驶入排序区内的多车道,使得驶入排序区内的车辆要进行车道选择,此时车道选择主要取决于排序区内车道与车辆当前车道的位置关系,故会在预停车线形成分流冲突.
(4) 排序区内合流冲突.排阵式信号交叉口的合流冲突主要发生在3个时段,分别发生于车辆驶入排序区时选择排序区内部车道的合流、主信号绿灯时段排序区内后方车辆争抢通过交叉口与旁侧排队车流的合流以及预信号绿灯末期加速进入排序区的车辆与驶离排序区车流的合流所产生的合流冲突.以上3类合流冲突中,第1类合流冲突是影响较为显著,同时也是排序式信号控制所特有的合流冲突.
根据上述分析可知,排阵式信号控制交叉口的交通冲突主要发生在排序区内部,同时排序区也是排阵式信号控制方法的关键,因此本文主要以排序区内的交通冲突及其影响为重点进行排阵式交叉口运行安全分析.
2.2 评价指标选取及划分
交通冲突根据影响程度的差异通常分为严重冲突、轻微冲突和潜在冲突等3类[14],为准确划分交通冲突的严重程度等级,本文选用PET(post encroach time)作为评价排阵式信号控制交叉口交通冲突严重性的判定指标.与TTC(time to collision)相比,PET只需测量前车离开冲突点的时刻及后车抵达冲突点的时刻,其预测难度较低,且数据有效性强.
此外,为确定采用PET为判定指标后的严重程度等级划分,本文采用SSAM模型中的5 s为PET最大临界值[18],并采用了PET数据累计频率曲线的拐点为临界点进行等级分类依据.
2.3 统计模型
2.3.1模型建立
选取有序概率模型分析排阵式信号交叉口冲突严重程度的显著影响因素,该模型已广泛使用在交通安全评价领域[19-20].交通冲突严重程度根据PET值可分为有序的3个等级,其数据结构与有序概率模型的固有性质相吻合,模型中交通冲突的严重程度由潜在变量y*决定,计算公式如下:
y*=αX+ε
(1)
式中:α为条件系数;X为自变量向量组;ε为随机干扰项.划分离散变量y的取值为表示严重冲突的y1,表示轻微冲突的y2,表示潜在冲突的y3,由此可得各离散变量概率如下:

(2)
式中:Π(·)为正态分布函数;χ1,χ2为临界待定参数,可通过最大似然估计标定[21].
2.3.2模型检验
根据统计数据对有序概率模型进行参数估计后,采用拟合优度系数R2(式(3))检验参数显著性,并通过式(4)和式(5)两个伪R2检验统计量对回归分析的有效性进行检验,即

(3)


(4)

(5)
式中:L0为零模型的似然函数;Lv为完整模型的似然函数;K为样本容量.
此外,为检验每个估计参数的显著性以筛选出对排阵式信号交叉口交通冲突严重性影响显著的变量,本文采用χ2检验(式(6)),并要求模型参数的显著性水平均不大于0.05.

(6)
式中:n为观测样本量;k为Xi可取集合元素数;Xi为n次观测中变量X取值为ai的次数;poi为原假设中变量值为ai的概率.
2.3.3边际效应
由于Ordered Probit模型中的自变量系数的符号与严重程度等级的概率变化方向并不完全一致[22],某变量系数的正负值智能反映该变量对y1和y3情况下的影响方向,而不能准确说明对于y2情况下影响方向,为进一步解释说明各影响因素对于交通冲突严重程度的影响方向及大小,需计算其的边际效应,其边际效应计算如下:
ΔP(yi|X)=α[φ(χi-1-αX)-φ(χi-αX)]
(7)
式中:φ(·)为标准正态分布的密度函数.
2.4 数据分析
为实现排阵式交叉口的交通安全分析,采集了深圳市南山区前海路排阵式信号交叉口连续4 d早晚高峰时段东、西进口道内段预停车线上游、排序区内部及交叉口内部的交通冲突点数、冲突类型、冲突严重程度指标等相关信息.此外,为更全面的研究排阵式交叉口的安全影响因素,还采集了排序区存储容量、预信号前排队车辆车头时距、是否存在二次冲突等相关变量.
根据采集的排阵式信号交叉口交通冲突数据,可得到如图2所示的PET分布图.由图2可知,PET值大于5 s的样本就有1%,符合临界值有效性.由交通冲突累计百分比,将第一个拐点(PET值小于或等于1.1 s,交通冲突累计数量的18%)的交通冲突定位严重冲突,其余的交通冲突平均分为两层,各约占41%,得到相应的PET值为1.9 s,作为轻微冲突与潜在冲突的临界值,根据以上划分方法,可得到排阵式信号交叉口交通冲突的严重程度划分,如表1所示.

图2 排阵式交叉口交通冲突PET分布
表1 排阵式信号交叉口交通冲突严重程度划分
Tab.1 Partition in severity of traffic conflict

严重程度PET范围/s样本占比事故风险潜在>1.939.8低轻微1.2—1.942.3中严重<1.217.9高
为对比排阵式交叉口的安全性能,本文选取与其交通组织及流量相近的两组常规信号交叉口进行各类交通冲突对比,3组信号交叉口的交通冲突对比结果如表2所示.
由表2可知,排阵式交叉口排序区处发生交通冲突的PET值均较大,表明排序区的设置可缓解左转车辆及直行车辆对其他车辆的交通冲突.其中,合流冲突方面排阵式交叉口百分比占比较大,原因是排序区的设置使得车辆在进入排序区选择车道时会产生合流现象,但并无显著差异.
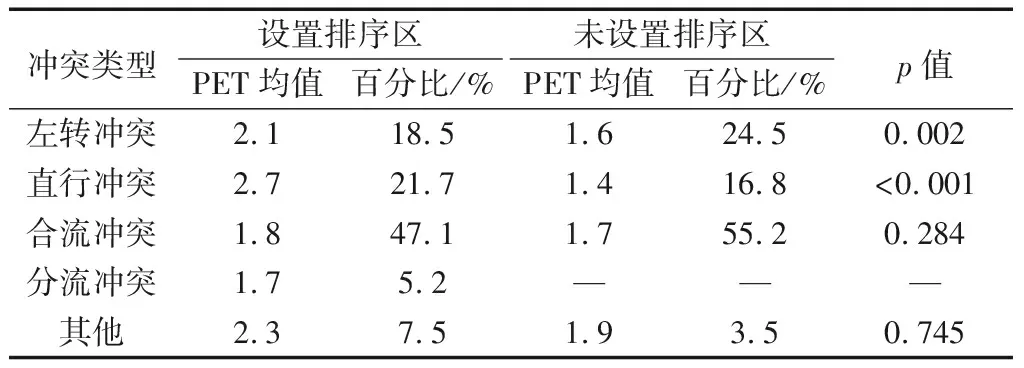
表2 交通冲突对比
本文采用SPSS软件进行有序概率模型的参数标定,采集排序区容量、排序区内数、左转交通量、直行交通量、排序区内车头间距、排序区各类交通冲突发生情况(0-1变量)、错误驾驶情况(违规进入排序区,0-1变量)等交通数据,并将所有收集的标量作为自变量,并对检测结果中p值大于0.05的变量进行排除后进行重新标定,保证标定变量对结果具有显著影响,得到最终参数标定结果,如表3所示,其中Nagelkerke-R2和Cox & Snell-R2值均大于0.2,可证明回归模型结果可接受.

表3 模型参数标定表
通过模型筛选出的相关变量与交通冲突严重程度有显著性影响,且均可与交通冲突发生概率呈正相关,表明增加变量取值将提高发生严重冲突的概率.由于变量系数无法解释对中间等级因变量的影响,为更好地描述解释变量对交通冲突程度的影响,需计算模型变量的边际效应,如表4所示.某个变量的边际效应便是在其他所有自变量都取均值,该变量取值增加一个单位时,严重程度等级的交通冲突发生概率的变化值.由表4可知,所有的自变量取值增加一个单位都会导致交通冲突严重程度的增大,同时左转及直行交通流量对于排阵式交叉口的交通安全影响程度较为明显.
由于排阵式信号交叉口的特殊设置,左转及直行交通流的流量成为影响排阵式信号交叉口及排序区车辆运行安全的主要影响因素.预信号、主信号的配时及协调控制同样受到交通流量的影响,在实际应用中,由于交通流量存在随机波动性,导致交通需求呈一定波动性.为了提高排阵式信号交叉口的交通安全,需要针对交通流量的随机波动进行优化控制,以提高排阵式信号交叉口的交通安全及运行效率.
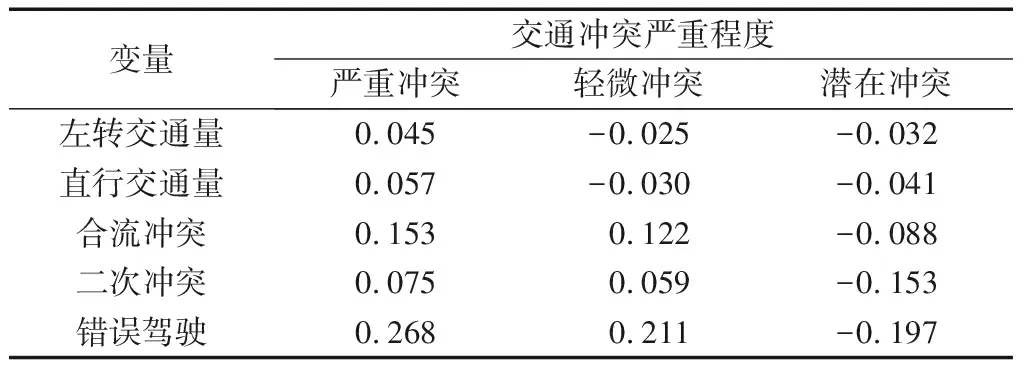
表4 边际效应对比
3 排阵式交叉口鲁棒优化模型
3.1 假设条件
(1) 排阵式信号交叉口的相位及相序确定;
(2) 各进口道交通流连续到达预停车线;
(3) 分析时段T共分为h个时间间隔,各时间间隔的交通流量随机波动.
3.2 模型建立
3.2.1目标函数
在不考虑交叉口行人流、非机动车流等慢行交通流的前提下,分别选择流量波动情况下,机动车延误指标最小、交叉口通行能力最大、进口道车辆停车率最小以及进口道最大排队长度最小为优化目标,建立多目标鲁棒优化模型如下:
minF(C,λi)=min[f1(C,λi),f2(C,λi),
f3(C,λi),f4(C,λi)]
式中:C为排阵式信号交叉口周期时长;λi表示第i相位绿信比;f1(C,λi)表示排阵式信号交叉口机动车车均延误标准差;f2(C,λi)表示排阵式信号交叉口通行能力;f3(C,λi)表示排阵式信号交叉口机动车平均停车率;f4(C,λi)表示排阵式信号交叉口进口道最大排队长度.
根据上述分析可知,交通流量随机变化是影响排阵式交叉口运行安全和运行效率的关键因素,因此本文选取机动车车均延误与标准差之和作为优化目标,其目的是使得排阵式信号交叉口能够适应交通流的随机波动变化,降低信号周期方案对于交通流量的敏感度,其目标函数式为
(8)
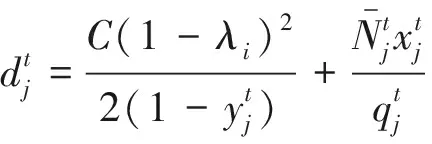
(9)

(10)

排阵式交叉口的设计初衷是为了提升交叉口的整体运行效率,本文选取交叉口通行能力作为优化目标,其目的是为了提高整个排阵式信号交叉口的通行效率,提升交叉口的服务水平.为便于计算,其目标函数为

(11)
式中:sj为第j车道的饱和流率.
排阵式交叉口的特殊控制方法使得车辆会在主、预信号处停车等待,但可通过调节主、预信号绿灯时间和间隔时间降低停车等待时间和影响.因此,选取机动车平均停车率作为优化目标是为了降低预停车线及主停车线处车辆延误时间,提高车辆在主、预停车线处的运行效率,其目标函数为

(12)
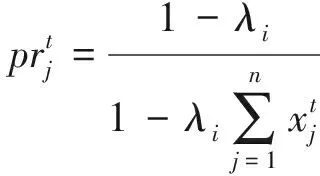
(13)

排阵式交叉口设置排序区,使得初始排队起始点后移,因此需控制预停车线前车辆排队以提高整体运行效果.因此,选取进口道最大排队长度作为优化目标是为了减少排阵式信号交叉口对下游交叉口的通行影响,其目标函数为
(14)
(15)
cj=sjλi
(16)

3.2.2约束条件
(1) 周期时长约束.周期时长不宜过短,应确保一个周期内到达预停车线处的车辆可以全部进入排序区内并排空;同时,周期时长不宜过长,以提高排阵式交叉口通行效率,即
Cmin≤C≤Cmax
(17)
式中:Cmin为最小周期时长;Cmax为最大周期时长.
(2) 有效绿灯时长约束.各相位有效绿灯时间不宜过短,降低通行延误,即
Cλi≥gimin
(18)
(3) 信号控制约束.各相位信号灯时间应满足交叉口通行需求,即

(19)
(4) 饱和度约束.本文模型建立基础为排阵式交叉口处于未饱和或饱和状态,过饱和状态本文模型不予讨论,即
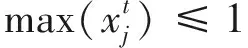
(20)
3.3 求解算法
传统多目标交叉口信号配时研究主要以符合决策者偏好的全局最优或局部最优解或解集为优化目标,但对于最优解的鲁棒性研究较少.因此,选取鲁棒度作为优化解的鲁棒性测量指标并计算最优平均有效函数,通过自适应LHS(latin hypercube sampling)法降低优化算法时间复杂度,同时应用改进的NSGA-II(non-dominated sorting genetic algorithm-II)算法搜索最优鲁棒解.
3.3.1最优平均有效函数算法
(1) 确定统计样本总体数量M;
(2) 划分周期时长C的邻域区间[C-δs,C+δs]为M个等距区间;
(3) 建立由数列{1,2,…,M}随机排列组成的列向量αM×1为随机变换列;
(4) 随机变换列的每一项对应一个总体样本中随机产生的个体样本,选出M个随机样本;


3.3.2自适应LHS鲁棒度算法
(1) 初始化精确度标量τ,设定单次迭代最小及最大样本数Mmin和Mmax:M1=Mmin,Mmax=M′+(k-1)ξ.式中,M′为抽样数量;k为解集的鲁棒度;ξ为平衡参数;
(2) 运用LHS抽样法抽取样本并计算相应优化目标属于f(x)的邻域η的百分比p1,令l=2,Ml=Mmax;
(3) 再次运用LHS抽样法抽取样本并计算优化目标属于f(x)的邻域η的百分比pl;
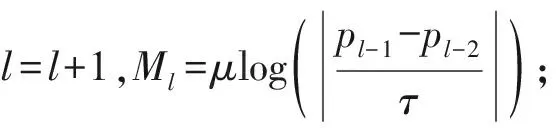
(5) 若k=1时,转至(6);否则,判断pk (6) 令k=k+1,返回(2). 3.3.3改进的NSGA-II算法 改进的NSGA-II搜索算法基于传统NSGA算法的基本思想上加入鲁棒度分析以获取鲁棒性较好的解集,其运算思想为:首先随机产生初始种群,经非支配排序后进行鲁棒度比较和集聚距离计算,选取鲁棒最优外部种群进行选择交叉及变异产生第一代子种群;随后,合并父种群与第一代子种群,经非支配排序后进行鲁棒度比较及集聚距离计算,选择适宜个体组成新的父种群;最后,通过遗传传递产生新的子种群,循环直至达到迭代阈值. 通过排阵式信号交叉口鲁棒优化模型及算法求解可得到信号配时方案解集,而选择最优配时方案解应当充分权衡决策者需求与决策矩阵的客观性.因此,本文应用主客观信息偏差最小法(MDASOI法(Minimum Deviation at Subjective and Objective Information))根据优化目标及效益指标之间的相关性,对排阵式信号控制的配时方案进行最优选择.设定信号配时方案解集为φ=(φ1,φ2,…,φp);评价指标为γ=(γ1,γ2,…,γq);区间指标权重向量为ν=(ν1,ν2,…,νq)T,0≤νi≤1. 3.4.1建立决策矩阵 假设信号配时方案解φi的对应评价指标γj的值yij(i=1,2,…,p;j=1,2,…,q),则可得到决策矩阵Yp×q=(yij)p×q.根据客观需求将决策属性指标分为效益属性、成本属性及区间属性3类.其中,效益属性旨在约束决策权效,属性值越大越优;成本属性旨在约束决策消耗,属性值越小越优;区间属性旨在约束决策变动,属性值越接近固定区间越优.3类决策属性标准化公式如下: 效益属性: (21) 成本属性: (22) 区间属性: θij= (23) 式中:a、b为最佳区间上、下限.由各效益属性可得效益标准化后的决策矩阵Ωp×q=(θij)p×q. 3.4.2确定区间指标权重向量 根据区间指标权重的选择及主、客观偏好信息的相对总误差,可得到权重向量优化函数如下: (24) 3.4.3决策方案选取 选取深圳市南山区前海路排阵式信号交叉口作为研究对象,统计早晚高峰(07:30—9:00、17:30—19:00)时段每5 min一段的交通流量,可得到分析时段内各时间间隔的交通流量值,各分析时段交通流量呈明显的随机波动性,如图3所示以某日早晚高峰交通量数据为例. 图3 高峰时段交通流量变化 此交叉口进口道渠化如图4所示,其中排序区长度为65 m,并在预停车线处设置虚线变换区,其信号配时方案如图5所示,其中排阵式信号控制方案仅在早晚高峰使用,平峰时段南北进口道仍使用常规信号控制. 图4 前海路学府路交叉口渠化 图5 前海路学府路交叉口信号配时 设定信号周期波动约束为50≤C≤150 s,各相位的最小绿灯时间为5 s,启动损失时间为8 s,建立排阵式信号交叉口鲁棒优化模型.应用改进的NSGA-II算法求解配时方案解集,并设定种群数量为200,进化迭代数上限为400,算子变异概率为0.05,算子交叉概率为0.95,鲁棒度为1~6,指定参数P=0.8. 图6为各优化目标的冲突性分析结果,图6a表明延误指标和平均停车率间存在明显冲突;图6b表明道路通行能力和最大排队长度不存在冲突性;图6c表明平均停车率和最大排队长度存在明显冲突.由此可知,延误指标和平均停车率、平均停车率和最大排队长度为有效优化目标,道路通行能力和最大排队长度并非有效优化目标. a 延误指标和平均停车率冲突曲线 b 道路通行能力和最大排队长度冲突曲线 c 平均停车率和最大排队长度冲突曲线 为检验改进的NSGA-II求解算法与传统NSGA-II算法的优化能力,在相同初始参数下应用两种算法进行对比分析,分析结果如图7a~7d所示.由对比结果可知,改进的NSGA-II算法所得通信能力较优,其他评价指标与NSGA-II算法相近,可知应用改进的NSGA-II算法可得到更好的优化配时方案解. a 延误指标对比 b 通行能力对比 c 平均停车率对比 d 最大排队长度对比 根据主、客观需求因素,将道路通行能力定为效益属性,平均停车率和排队长度定为成本属性,延误指标定为区间属性,同时将决策方案解集的鲁棒度定为效益属性并建立决策矩阵.求解鲁棒优化模型可得到区间指标权重向量,如表5所示.分别应用熵权TOPSIS法、区间TOPSIS法和MDASOI法对决策方案进行比较计算,计算结果如表6所示. 表5 区间指标权重参数表 表6 各决策算法结果对比表 由表6可知,与熵权TOPSIS法及区间TOPSIS法相比,MDASOI法可满足配时方案中主、客观需求,延误指标分别降低了28.80%和6.29%,最大排队长度分别降低了32.43%和7.41%,可整体提高排阵式交叉口的交通效益及安全性. 为检验本文鲁棒优化模型所得配时方案优化能力,本文选取传统配时方法与本文模型进行比较分析,分析结果如表7所示. 表7 各配时方法结果对比表 由表7可知,与HCM法及ARRB法相比,本文模型有较好优化效果,延误指标分别降低了18.99%和15.10% ,最大排队长度分别降低了26.47%和24.24%.排阵式交叉口的交通运行效率得到了明显提高. 为检验鲁棒优化模型的优化结果对排阵式信号交叉口交通安全的提升效果,根据实例数据并结合仿真软件对优化方案的各类交通冲突数据进行采集,并与实例数据进行对比,对比结果如表8所示.由表8可知,优化方案与实例方案相比,交叉口交通冲突的PET值均明显增大,表明优化方案可更多的缓解排阵式信号交叉口的交通冲突.其中,左转及直行冲突的PET均值分别提高了23.8%和11.1%,表明优化方案在交通流量随机波动下可明显提高排阵式限号交叉口的交通安全效益. 表8 优化方案与实例方案交通冲突对比 (1) 运用交通冲突技术对排阵式交叉口进行交通安全分析,选取PET值为交通冲突评价指标,计算结果显示交通流量和二次冲突为主要影响因素,其中交通流量对交通冲突严重程度影响较为显著; (2) 在考虑进口道交通流量随机波动性的情况下建立了排阵式交叉口鲁棒优化模型,并将延误指标、通行能力、平均停车率及预停车线前最大排队长度作为优化目标,并应用改进的NSGA-II算法进行模型求解,并通过MDASOI法进行决策分析; (3) 选取实例进行计算分析,分析结果显示排阵式交叉口延误指标和平均停车率间存在明显冲突,道路通行能力和最大排队长度不存在冲突性,平均停车率和最大排队长度存在明显冲突;与传统NSGA-II算法相比,改进算法可明显提高优化解;与传统决策方法相比,本文模型可有效解决主客观需求问题,得到最优决策方案;与传统HCM和ARRB相比,本文模型可降低延误指标约28.80%和6.29%,降低最大排队长度约32.43%和7.41% (4) 通过优化方案与实例方案的交通冲突数据对比显示,优化方案可更多的缓解排阵式信号交叉口的交通冲突,同时与实例方案相比,左转及直行冲突的缓解程度分别提高了23.8%和11.1%,提高了整个交叉口的交通安全效益.但本文相位相序及排阵式组织形式较为固定,在实际应用中交通流量及其他因素的影响有待进一步的研究.3.4 决策分析
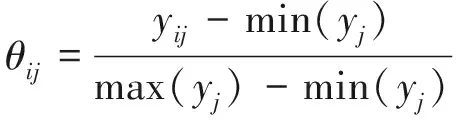

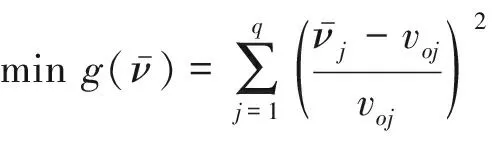

4 实例分析
4.1 数据采集
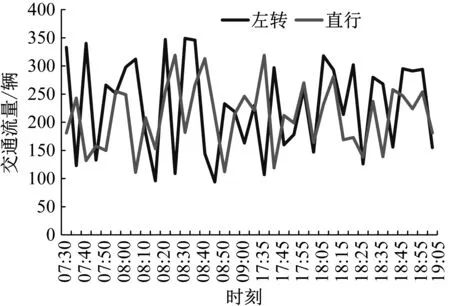



4.2 优化目标分析
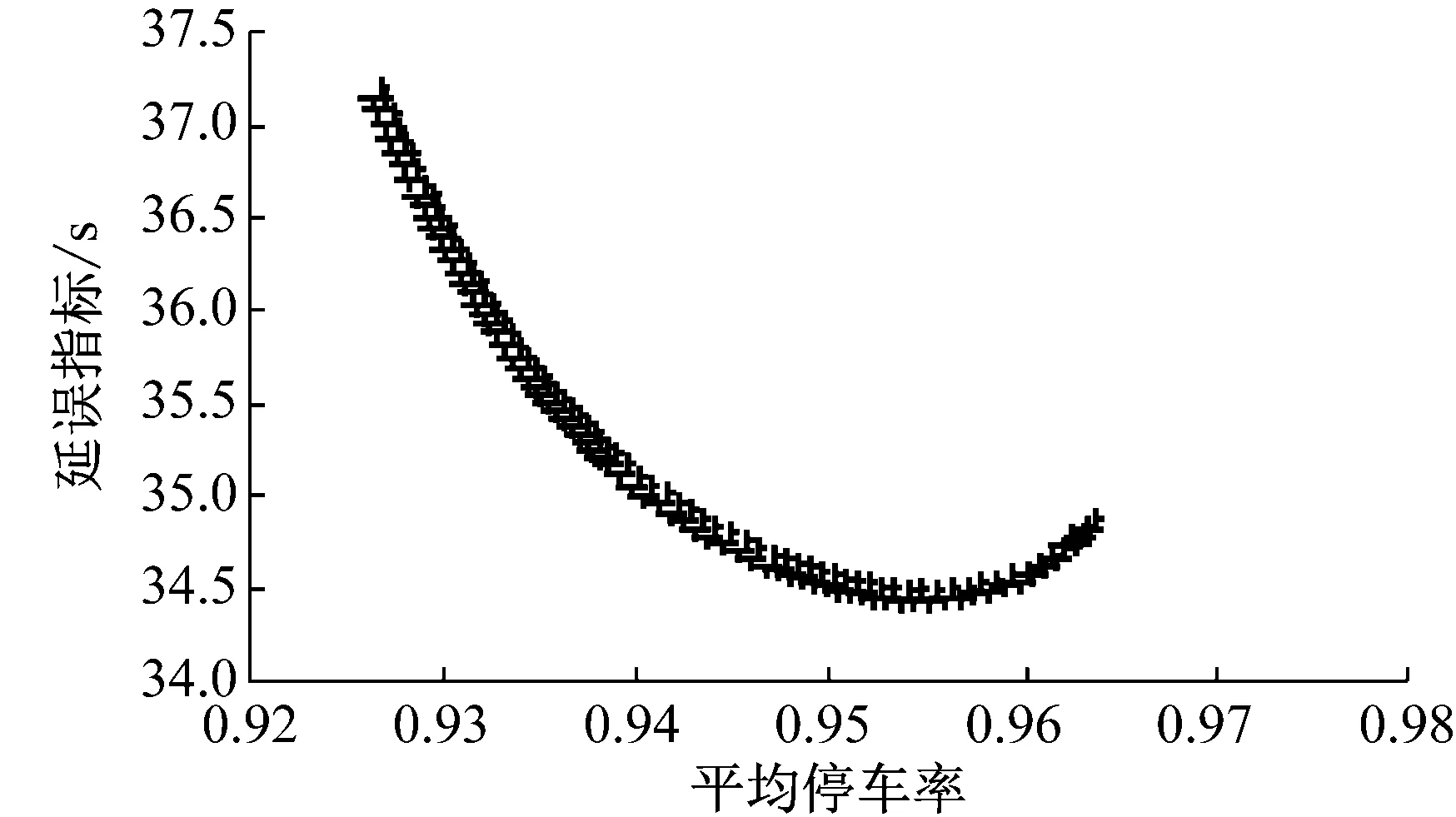
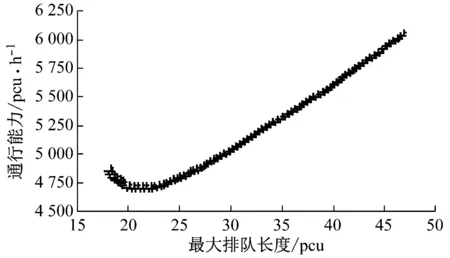

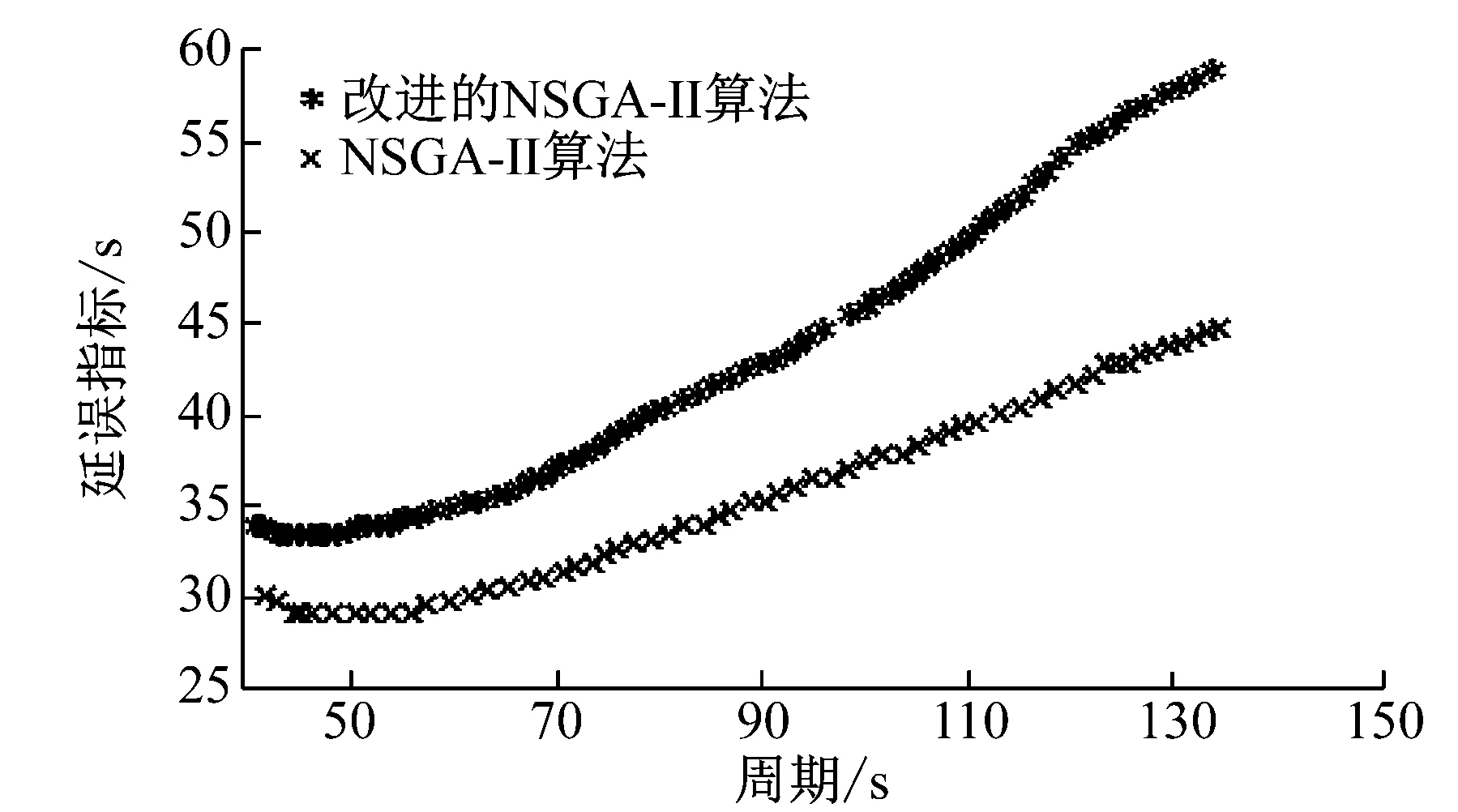



4.3 配时方案对比

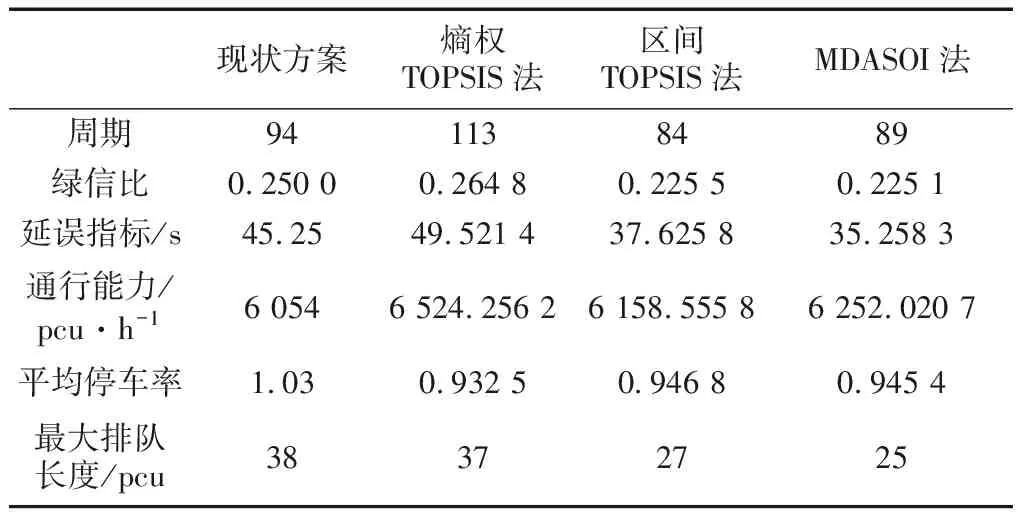
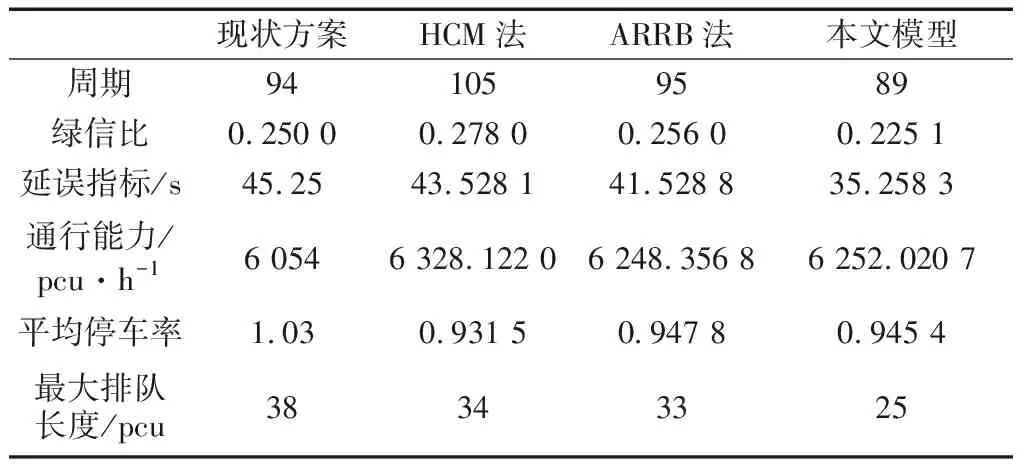
4.4 交通冲突对比

5 结论

