增材制造中耦合零件表面粗糙度及支撑面积的建造方向优化

王 玉， 陈子谦， 李后起， 高庆勇， 胡志桥， 于 颖

(1.同济大学 中德工程学院， 上海 201804； 2.同济大学 机械与能源工程学院， 上海 201804)

熔融沉积(fused deposition modeling, FDM)制造技术目前已成为发展最快的增材制造技术之一，由于其建造柔性，不同的建造方式对零件性能会产生较大影响，其中尤以建造方向对零件性能的影响最大.在成型零件的性能中，表面粗糙度是一个重要的评定标准，特别是零件的某些功能性表面，往往对其表面粗糙度有特定要求.在FDM制造技术中，影响表面质量的因素有很多，包括层厚、成型方向、打印参数(速度、温度)、填充密度、支撑结构等都会影响最后的零件表面质量.意大利学者Boschetto等[1]通过大量实验数据的分析，得出了30°～150°范围内，影响表面质量的因素主要为层厚和成型方向，并以此为基础，提出了在FDM技术中表面粗糙度Ra的公式.韩国教授Ahn等[2]和其团队发现了成型角度在0°～30°和150°～180°范围内，模型预测值和实际测量值会出现较大的偏差.对于成型零件表面粗糙度的优化问题，Pandey等[3]考虑了表面精度和打印时间两个优化目标，使用遗传算法NSGA-II来确定Pareto解集，该方法主要适用于FDM.

理论上，增材制造技术可以用于任何复杂型面的加工制造，但是当涉及到零件精度时，支撑问题成为限制其使用的主要因素之一.零件支撑是增材制造过程中的一个重要环节.FDM制造过程类似于“堆积木”，从下往上逐层堆积，如果上下两层丝材位置偏离程度较大时，挤出头挤出的熔融丝材来不及和下层固化层黏结就会坠落，打印无法顺利进行.而对于零件支撑面积，往往越小越好，一方面节省材料，另一方面，较小的支撑面积意味着支撑材料去除后较小的零件表面损坏面积.目前对于零件支撑结构的研究主要集中在如何寻找支撑部位和如何添加支撑结构上.支撑对于建造方向的优化问题，通常和其他性能联系在一起研究，诸如打印时间和零件表面质量，因此诸多学者在此领域建立了多目标优化算法[4-6].

目前各学者的研究中，未提出在0°～180°范围内能较好预测成型零件表面粗糙度的模型，往往在较小角度范围和较大角度范围的预测上存在较大误差；未提出性能耦合下表面粗糙度和支撑面积的优化问题.FDM增材制造中，建造方向扮演着重要角色，一方面影响着支撑结构的产生和成型零件的表面粗糙度；另一方面，建造方向的选择处于零件增材制造的前期处理阶段，易于调整.本文就FDM制造过程中不同建造方向下，零件表面粗糙度的预测，表面粗糙度和支撑面积这两个性能的优化，以及多因素耦合下的多目标优化问题进行了探讨.

1 基于零件表面粗糙度的建造方向优化

由于成型表面主要受熔融沉积加工过程中的台阶效应影响，因此成型方向和分层厚度对于表面质量的影响最为重要[7].在实际制造过程中，缩小层厚虽然可以降低表面粗糙度，但当分层厚度减小一倍，则理论上加工时间增加一倍.而成型方向对于总体加工时间的影响则柔性很多.这里主要通过图1所示思路研究建造方向对于表面粗糙度的影响，建立优化算法选择最佳建造方向.

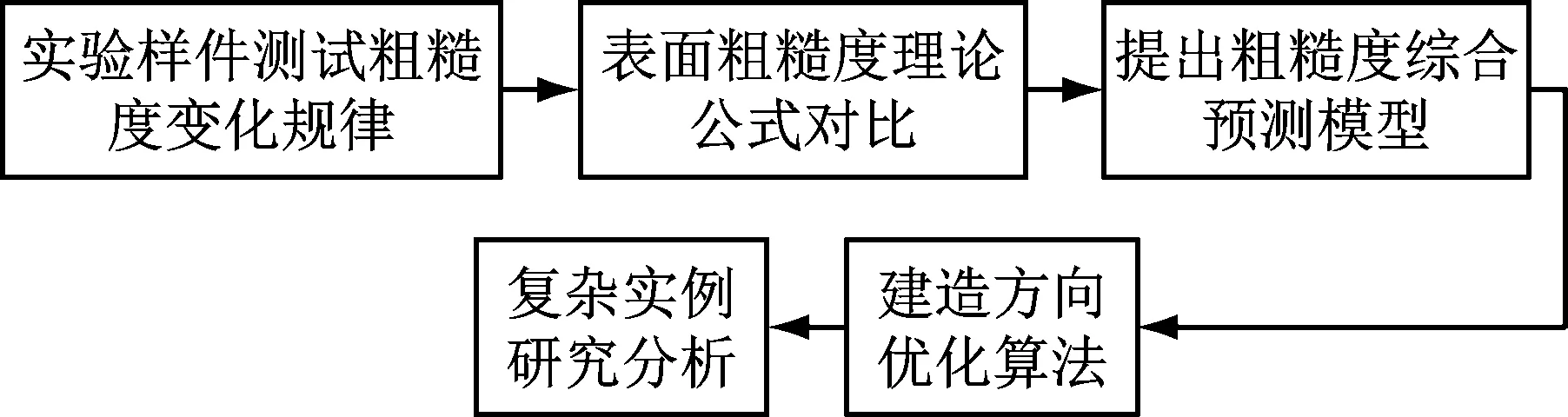
图1 技术路线

1.1 FDM成型零件表面粗糙度理论公式实验研究

使用Truncheon测试零件进行不同建造角度下表面粗糙度的测量验证[8].考虑到打印时间和打印机的尺寸等，设计Truncheon测试零件递进角度为5°，总共包含19个四方体，每个四方体尺寸为10 mm×20 mm×20 mm，整体尺寸为210 mm×20 mm×20 mm，打印材料选用聚乳酸(polylactic acid, PLA).通过打印后的成品(图2)可以看到，成型角度在90°范围附近，FDM技术成型零件表面质量较好，随着成型角度的变化，样件的粗糙度逐渐恶化，整体粗糙度变化趋势符合理论计算模型中的描述.

图2 Truncheon测试样件

采用探针式表面粗糙度轮廓仪，对成型零件的表面粗糙度进行测量.利用轮廓算术平均偏差Ra公式和阶梯斜高计算公式推导出的表面粗糙度理论计算公式为[9]

(1)

式中:lt为层厚;θ为成型角度.

将成型零件的表面粗糙度测试值与理论计算公式进行对比,见图3，可发现实际测得的表面粗糙度数值与理论公式得到的值存在误差：① 0°～10°范围内存在着明显的背离趋势；② 10°～70°,110°～170°范围内粗糙度呈现减小的趋势，但实验值明显小于理论值；③ 80°～100°范围内理论公式在90°位置趋近于0，而实际测得的数值趋于平稳，大于理论数值.

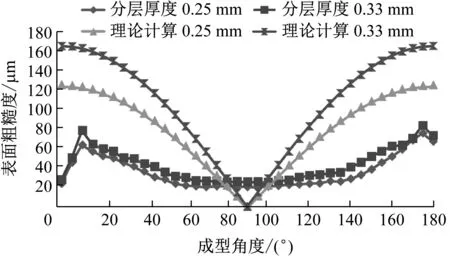
图3 实际表面粗糙度测试结果和理论公式对比

Fig.3 Comparison of measured results of actual surface roughness and theoretical formulas

1.2 表面粗糙度预测模型的建立

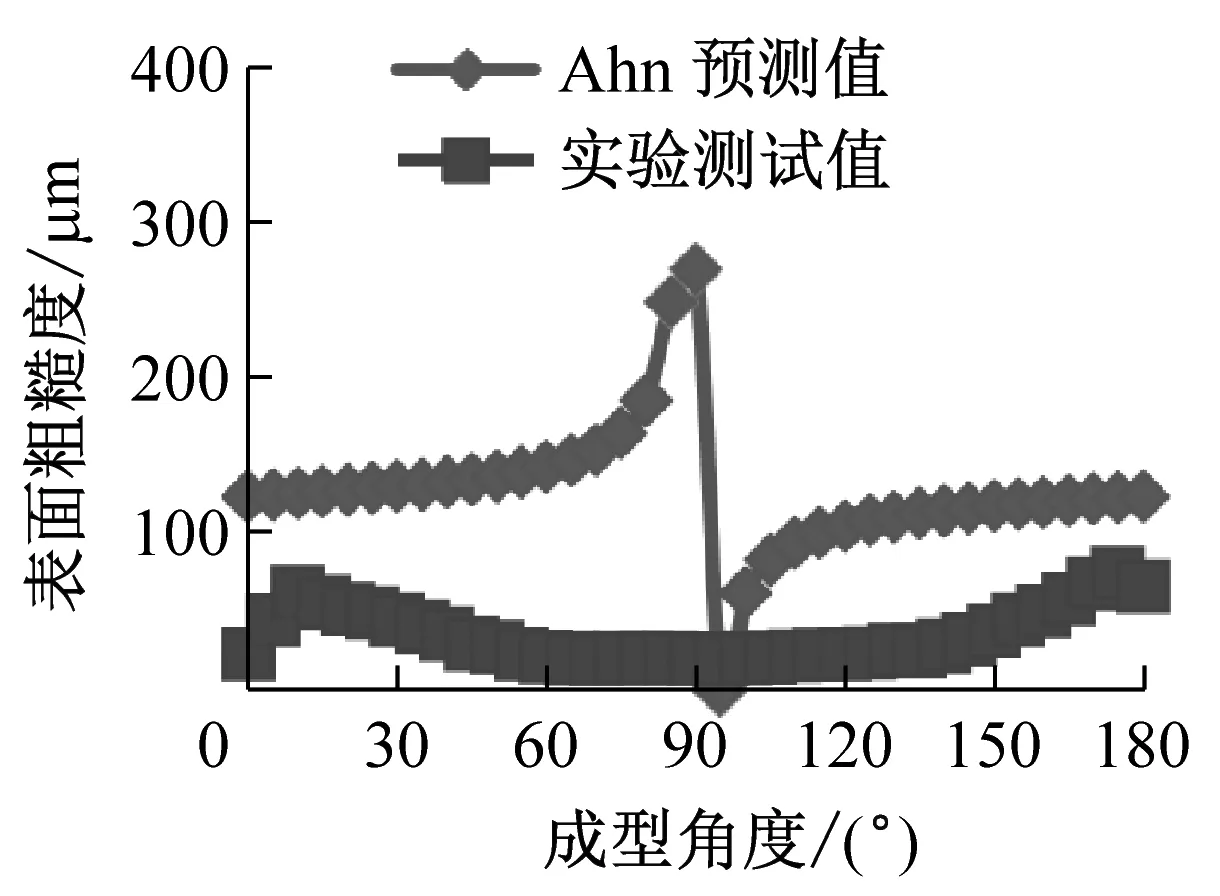
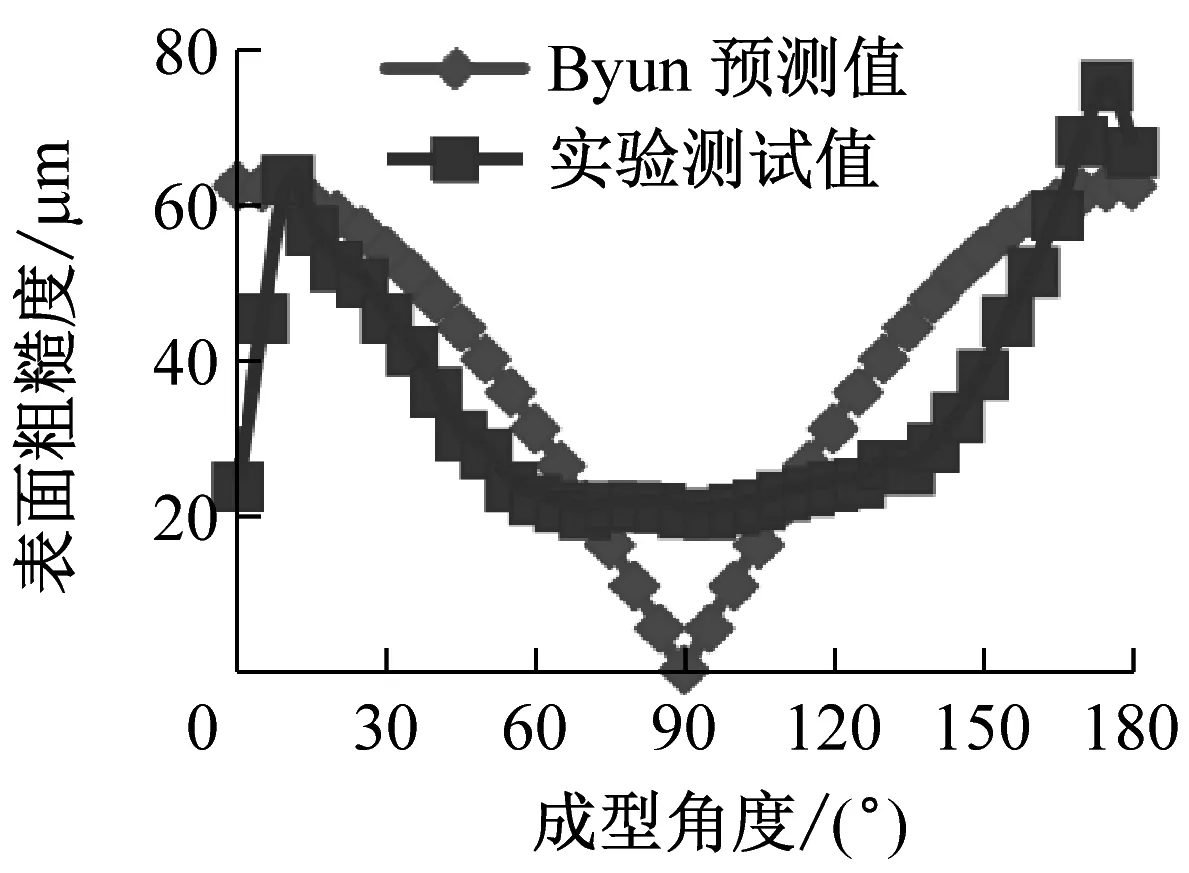
对于表面粗糙度的预测模型，Campbell，Mason，Byun等人都做出了研究并提出了理论公式.每个模型对于外层丝材沉积轮廓的描述都做了不同的假设，包括了矩形、椭圆形以及抛物线形等等，进而分别给出了熔融沉积表面粗糙度的预测公式.下面将Campbell等[10]、Mason[11]、Byun等[12]、Ahn等[13]、Pandey等[14]、Boschetto等[1]分别提出的较为著名的经验预测公式与标准测试零件在分层厚度0.25 mm下测得的实验数据进行对比,结果见图4.

实验发现,不同的经验公式各有利弊，通常在某一范围内给出了较为精确的预测，而在其他成型角度，预测值和实际值往往差距过大：①Campbell和Boschetto的预测公式在0°～20°和160°～180°范围内的值远大于实际测量值；②Mason的预测公式的值普遍大于实际测量值；③Ahn的预测公式的值普遍大于实际测量值，0°～90°范围内的值的变化趋势与实际测量值变化趋势相背离，且在成型角度90°处的值出现跳跃；④Byun的预测公式在70°～110°范围内的值远小于实际测量值；⑤Pandey的预测公式在170°～180°范围内的值大于实际测量值.

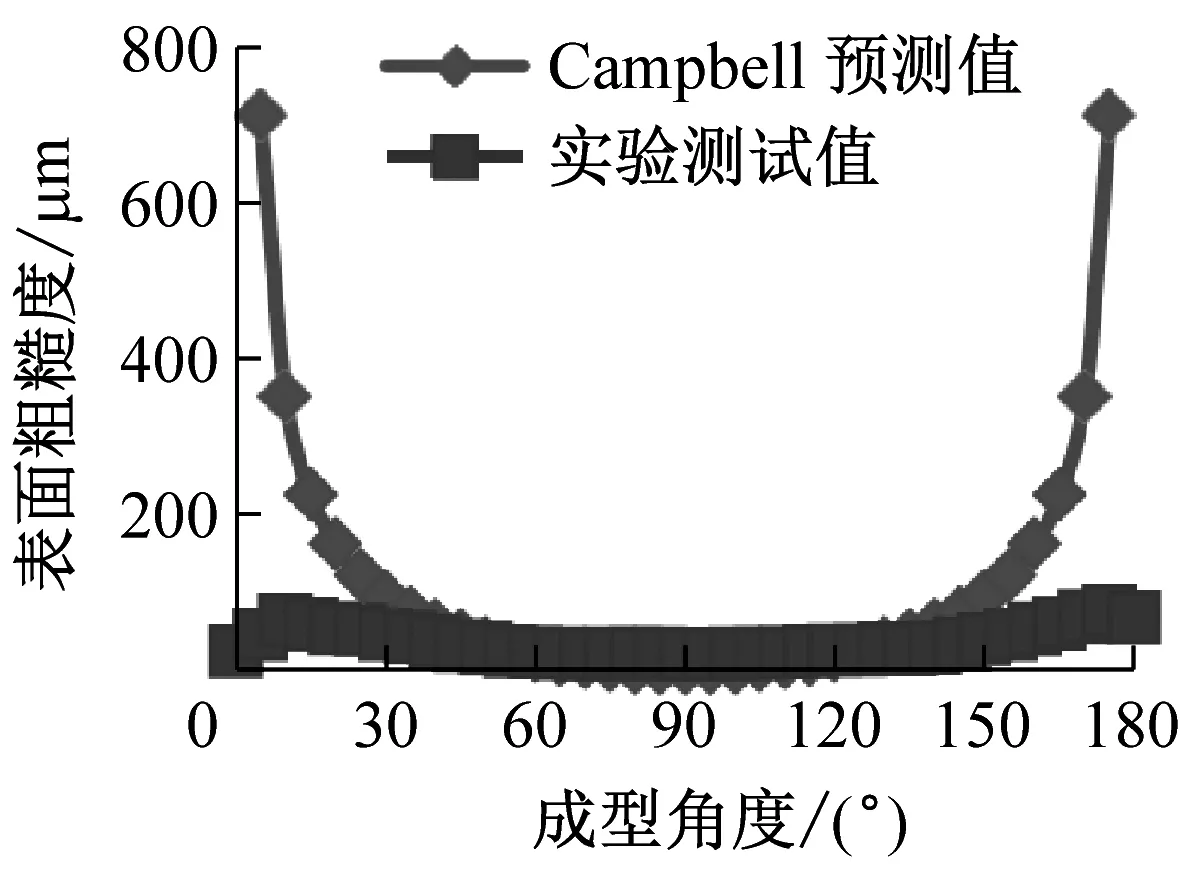
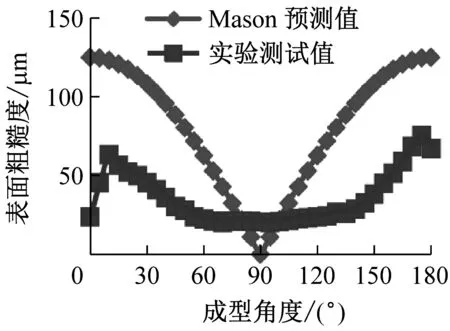
在此选用平均绝对百分误差e1作为衡量预测模型好坏的标准.

(2)

式中:Qt表示某一建造方向的实验值；Ft为该方向的预测值；n为建造方向的个数.

结合实验的结果，将成型角度分为4个范围，分别为0°～20°，20°～90°，90°～135°，135°～180°.通过e1值对不同成型角度区间内对应的不同经验公式进行对比，见图5.由图5可以看出，在各个范围内，分别为Pandey，Boschetto，Pandey，Byun所建立的模型e1值最低.

基于以上的分段分析，建立了新的综合粗糙度预测模型.对于任意建造方向，其表面粗糙度计算公式如下：

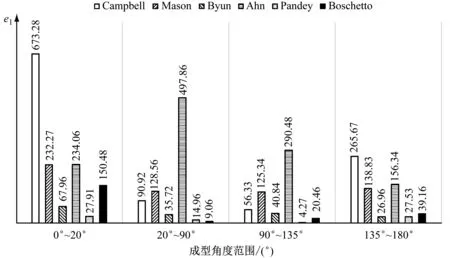
图5 各经验公式e1对比

Fig.5 Comparison ofe1of empirical formulas

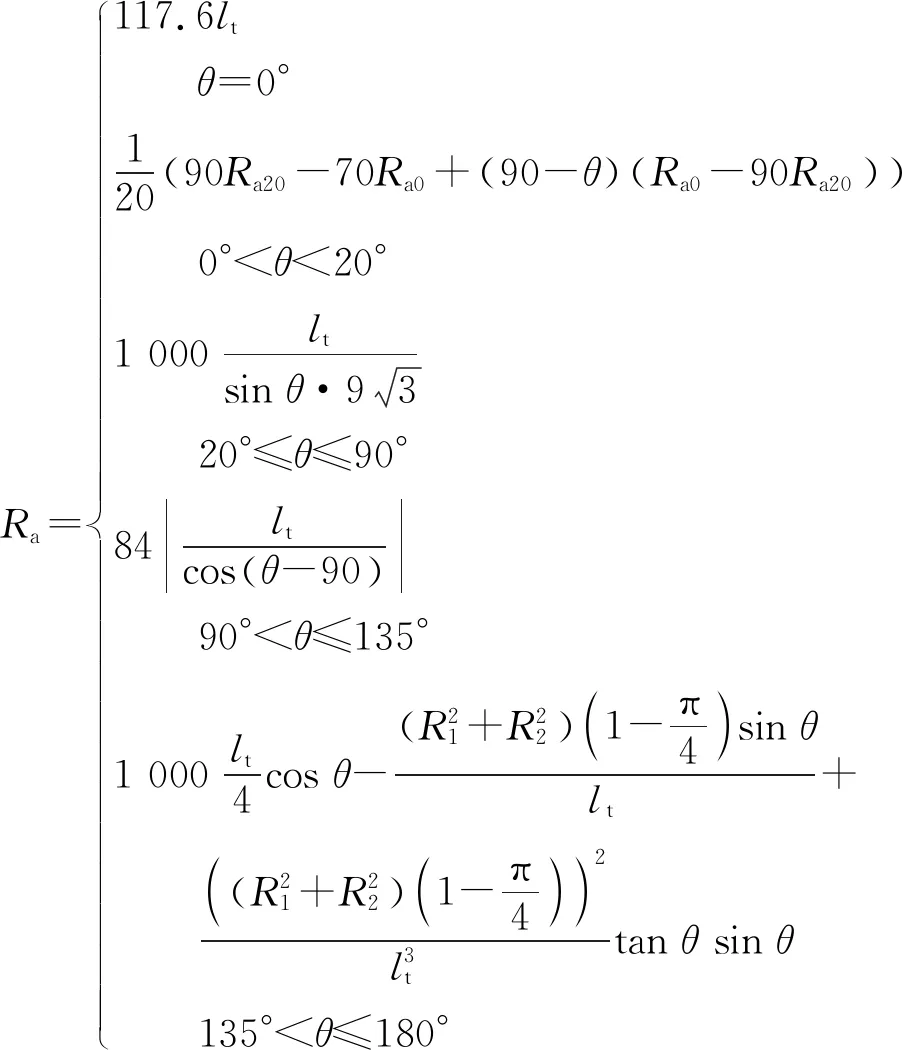
(3)

式中:如图6所示，lt为层厚,mm；θ为建造方向与打印表面法向量的夹角,(°)；R1为圆角半径，对于FDM制造工艺取0.045 mm；R2为基部圆角半径,取0.01 mm；Ra20为θ角等于20°时的粗糙度，Ra0为θ角等于0°时的粗糙度.

将样品实验测试值与综合预测模型进行对比，从图7可以看出，在0°～180°范围内，综合预测模型的预测值均能较好反映出实际测试值，其误差范围平均保持在10 μm以内，避免了前述经验预测公式在小角度(0°～20°)及大角度(135°～180°)范围内出现的较大误差情况，能够较为全面地反映表面粗糙度的变化情况.另外由于各个角度范围内选取了e1值最小情况的经验公式，故整体的e1值相较于单一理论模型的值减小，同时对于分层厚度为0.25 mm和0.33 mm两种情况其一致性较好.

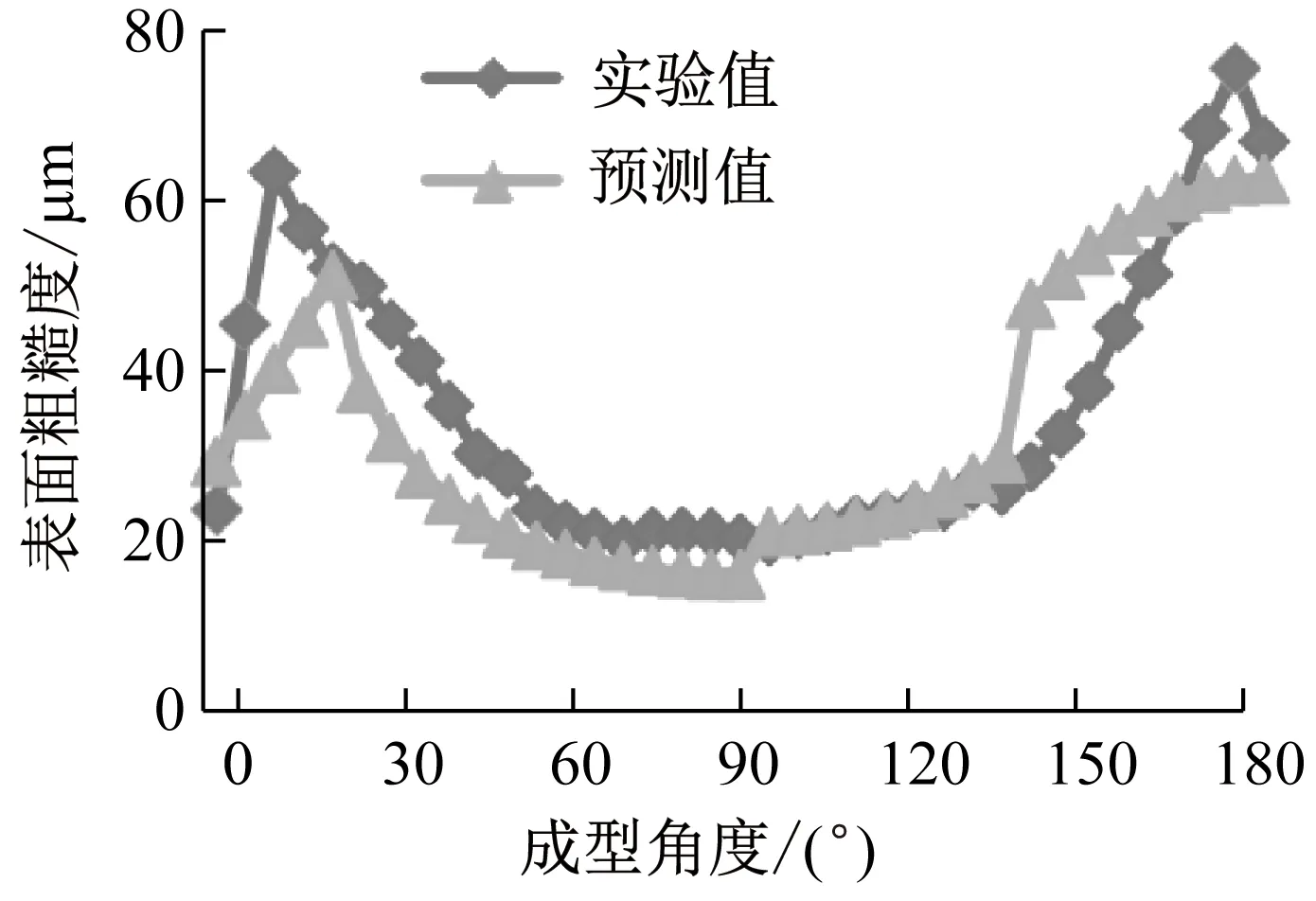
a 分层厚度0.25 mm

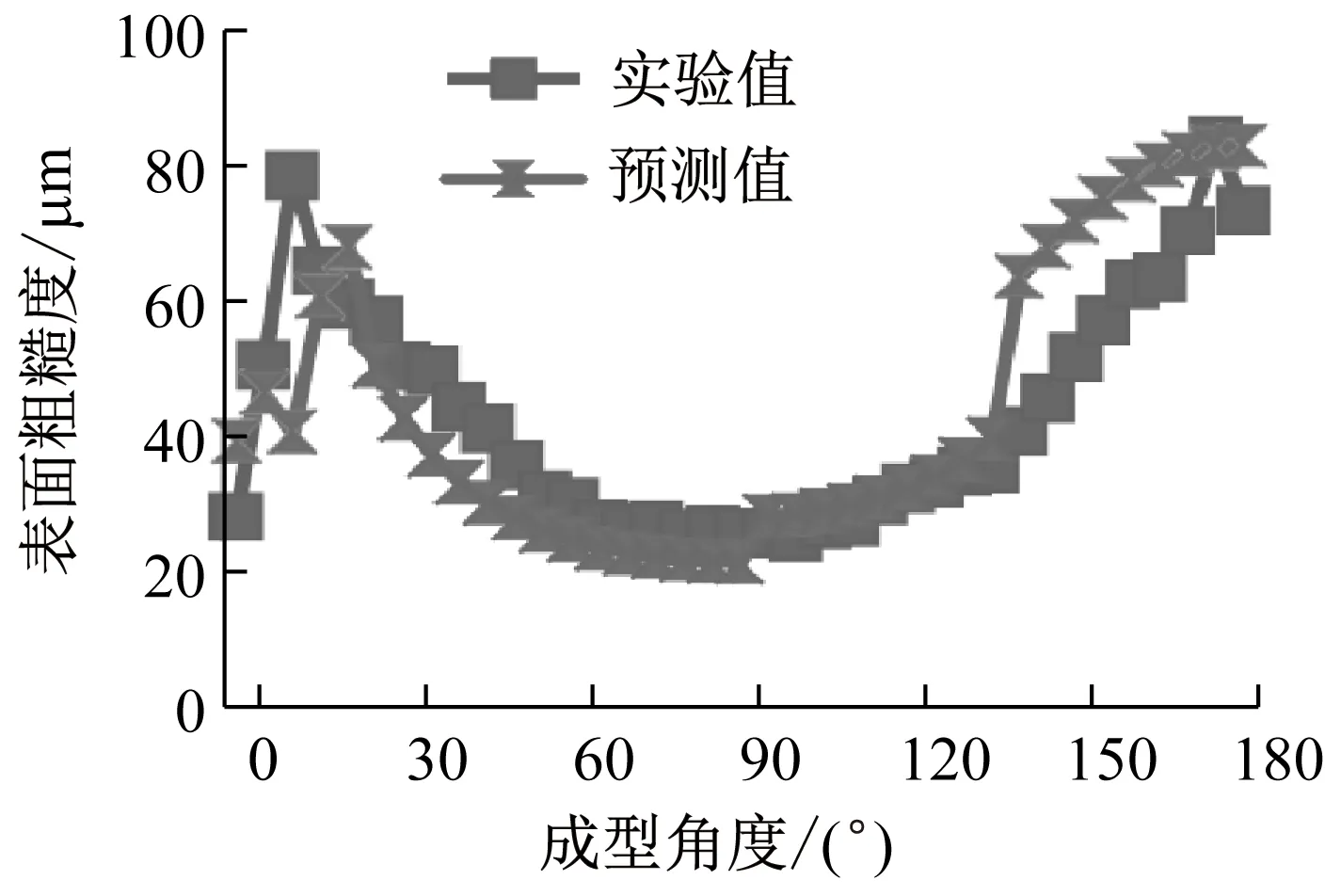
b 分层厚度0.33 mm

1.3 基于功能性表面粗糙度的建造方向优化算法

面对简单的零件，角度的调整较为直观简单.而对于较为复杂的零件，需要考虑到其功能性表面的制造要求，如某些零件表面需要和其他零件表面接触，起到密封作用或是有相对滑动，这一类表面的粗糙度会有特殊标注，工艺上粗糙度必须符合一定的范围要求才能满足诸如保证密封、减小摩擦之类的工艺要求.

确定各个功能性表面后，根据每个表面对应的最佳建造方向，得到最佳建造方向集合.最佳建造方向的选择需要考虑零件特征的对称性(几何)、可加工性以及增材制造的工艺特性等因素.例如，为减小表面粗糙度及得到较好的成型效果，对于平面特征，其最佳建造方向为平行于平面法线的方向；对于柱面或孔特征，其最佳建造方向为平行于其轴线方向.另外，对于具有较为复杂几何外形(同时具备多种几何特征)的零件，选择多个几何特征作为功能性表面后，需要综合考虑的因素较多，此时可供选择建造方向集合的元素往往多于选择的功能性表面的数量.

这里使用前文中建立的表面粗糙度综合预测模型分别计算集合内各建造方向下零件整体的表面粗糙度，选择整体粗糙度最小的方向作为最优建造方向.

建立优化算法，见图8，首先根据初始模型和功能性要求，选择功能性表面.之后通过功能性表面最优建造方向准则，确定建造方向集合.在初步得到建造方向集合之后，通过外部诸如加工条件、装配条件以及标准化的限制，进一步对建造方向集合进行筛选，得到最终集合.随后通过MATLAB软件开发，将集合内的建造方向分别输入程序.在一个建造方向下，遍历零件所有的光固化立体造型术文件格式(stereolithography, STL)下的三角面片，根据三角面片中法方向信息计算该面片和建造方向的夹角，使用上文中建立的综合粗糙度预测模型对每一个三角面片进行表面粗糙度的计算.每个面片的粗糙度乘以该面片的面积，得到整体零件的粗糙度情况.最后除以零件的整体表面积求得表面粗糙度的平均值.通过比较不同建造方向下的平均表面粗糙度，得到整体粗糙度最优的建造方向.

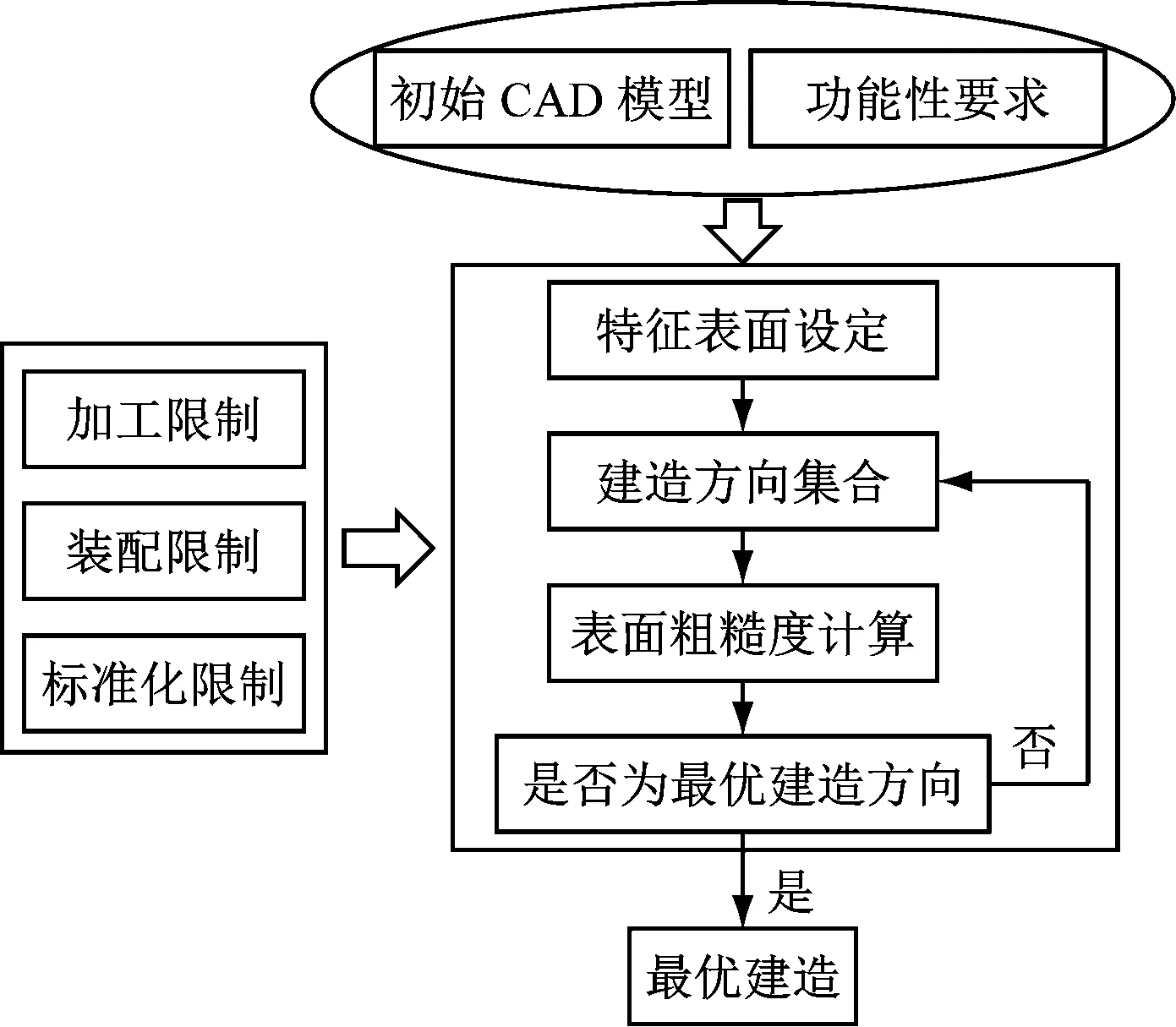
图8 优化算法流程图

2 耦合支撑面积及表面粗糙度的建造方向优化

在制造过程中，工程师总是希望支撑材料越少越好，一方面是考虑到节省材料的问题，因为这些支撑材料需要被去除；另一方面，外力去除支撑的过程中也会对已经成型的表面产生破坏，从而影响表面质量.

2.1 基于支撑面积的建造方向优化数学模型

支撑面积就是打印过程中需要生成支撑结构以完成打印的零件表面在成型平台的投影面积.本文针对STL格式的数据进行分析研究，规定当三角面片的法方向与建造方向的夹角大于90°时，该三角面片的朝向向下.对于常用的桌面级FDM打印机，通常夹角大于135°时，系统默认底部需要支撑结构，如图9所示.

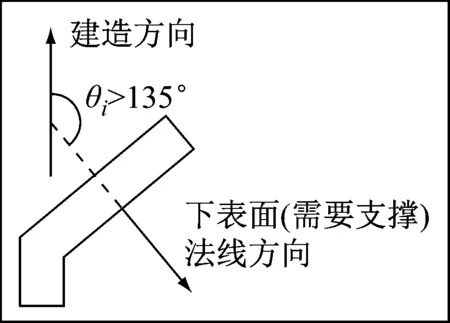
图9 零件表面支撑结构生成条件

因此在建模时，以135°角为阈值，计算STL模型中，法向量与建造方向夹角大于135°的三角形面片到成型平台的投影面积的总和，其数学模型如下：

f1(θi)=min ∑|Ai·cosθi·δ|

(4)

式中:δ为阈值函数；θi为三角面片法方向和建造方向的夹角；Ai为三角面片的面积.设建造方向的单位向量Np=x+y+z，建造方向Np与z轴的夹角为β，Np在XOY平面的投影与x轴的夹角为α，则x,y,z可表示为

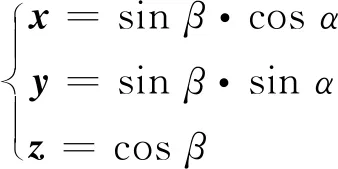
(5)

其中0 ≤α≤ 2π，0 ≤β≤π.这样，在求建造方向时，x,y,z三个变量就转化为α和β.通过程序遍历STL格式中所有三角面片的法方向，进而将建造方向转化为球坐标系的变量α和β，在0 ≤α≤ 2π，0 ≤β≤ π范围内，通过步进α和β的值，来展现全部建造方向内的支撑面积变化情况.

2.2 耦合表面粗糙度和支撑面积的建造方向优化数学模型

由前述模型及实验结果可知，关于建造方向分别对于零件整体表面粗糙度和支撑面积的影响存在着以下几个问题：①由图4、图7可知，虽然0°和90°的建造方向对于功能性表面的表面粗糙度最好，但是对于一个90°的平面，在60°～135°的建造方向范围内，粗糙度的增幅是不明显的，因此对于功能性表面的建造方向准则，可以允许一定角度内的偏离；②有限数量的建造方向的集合，往往可能漏掉全局最优解.因此需要一个更加精确的方法，遍历整个建造方向空间，全局搜寻最优解；③在FDM制造中，以上两个性能往往存在着耦合.提升其中某一个性能指标的同时，往往会造成另一个性能的恶化.

由于涉及到的角度变量范围较大，涉及到的数据量较多，需要进行大量的计算，同时为了在较大的角度范围内得到最优解，避免陷入局部较小值，可以使用遗传算法来解决.对于第三个问题，同时考虑到两个质量因素，由于涉及两个目标函数，因此该问题需转化为多目标优化问题，根据不同目标的重要性，可以得到一组最优解集.

(1) 以支撑面积为目标的数学模型，即为前述公式(4).

(2) 以表面粗糙度为优化目标的数学模型

f2(θ)=min ∑AiCi

(6)

式中:Ci为三角面片的粗糙度;Ai为三角面片的面积.

在此引入权重ωi，将多目标函数整合为一个单目标函数.

minf(x)=∑ωifi(x)

(7)

对于权重的选择，主要依据各个目标的重要性，需要和相关设计人员进行沟通.考虑到支撑面积与表面粗糙度在此多目标化问题中的同等重要性，因此分别将两目标函数的权重设为 0.5.另外，f1和f2的量纲不同，f2的计算值远大于f1.由于|cosθ|取值区间为[0,1],因此这里对表面粗糙度Ci进行归一化处理.

(8)

式中:Ci为三角面片的粗糙度，由前述综合粗糙度预测模型计算得出；Cmax、Cmin分别为粗糙度最大和最小的两种情况，对于0.25 mm的分层厚度，粗糙度最大值和最小值分别为65.0 μm和16.5 μm.

3 综合算例

建立零件模型对上述提出的优化算法及数学模型进行实例运算.零件为带有不同特征的多表面零件体，见图10，包括两个面分别带有通孔的呈L型的底座和与底面夹角为60°的圆柱台阶.打印材料为PLA，打印温度为180～200 ℃，打印速度为50mm·s-1.

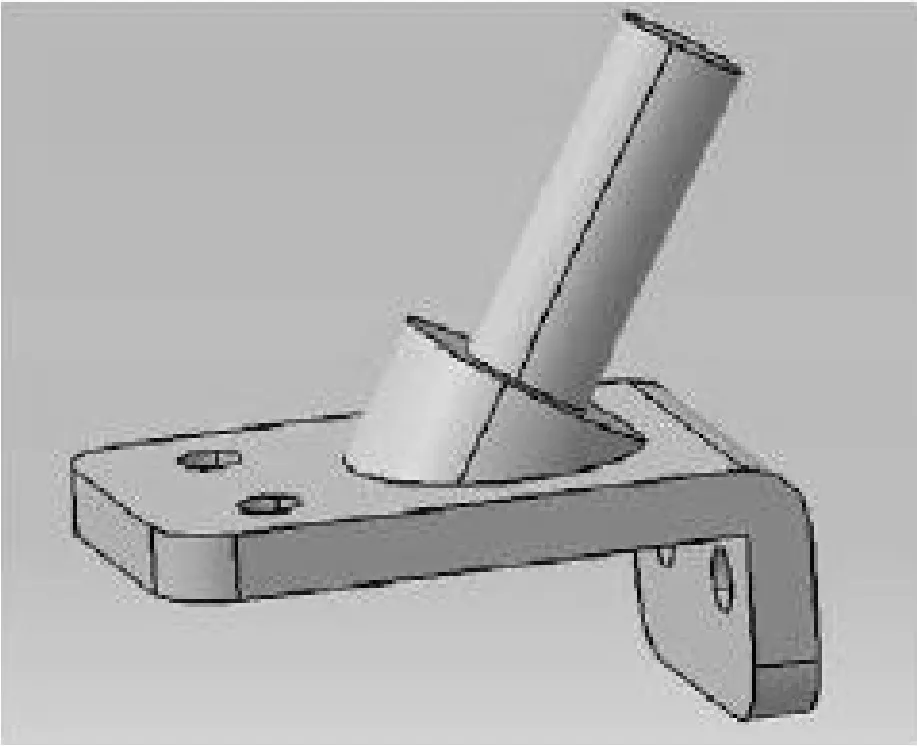
图10 零件模型

在测试不同建造方向下的支撑面积以及表面粗糙度时，需要进行大量的计算，因此考虑使用遗传算法来解决该问题.遗传算法是一种模拟自然选择和遗传机制的寻优方法，通过筛选对环境适应强的基因进行保留，进而基因杂交产生新的后代，保证了适应度较高的基因存活下来.同时为了防止种群的过早成熟，通过一定程度的变异，将新的基因带入种群中，丰富种群多样性.在标准遗传算法中，主要运行参数包括数据结构、初始种群个数、进化代数、适应度、选择算子、交叉概率、变异概率等.

3.1 基于功能性表面建造方向优化

选取L型底座上表面及圆柱台阶圆柱面作为特征表面，见图11.通过MATLAB软件读取零件STL格式文件.该零件的三角片面个数348个，零件整体表面积5 844 mm2.基于确定的功能性表面，为使得建造方向的选择最大程度考虑零件几何特征、增材制造工艺特性以及可加工性等因素，最终确定建造方向集合，见表1.考虑到零件在建造平台上的放置稳定性，最大程度减小支撑面积，共选取5个建造方向，与此同时，方向1的选择考虑到底座上表面这一特征面的制造特征(建造方向垂直于平面)，方向2的选择考虑到了避免底座下部所需的大面积支撑，方向3的选择同方向2，方向4的选择同时避免了L形台阶垂直边所需支撑，方向5的选择考虑到圆柱形台阶圆柱面这一特征面的制造特征(建造方向平行于圆柱轴线)，其中坐标轴方向定义如图12a所示.实例中设置零件分层厚度为0.25 mm.使用前文所建立的综合粗糙度预测模型，计算可得各个建造方向下的平均表面粗糙度的值，见表2.其中，建造方向2使得整体表面粗糙度最小，选择其作为基于功能性表面的最优建造方向.

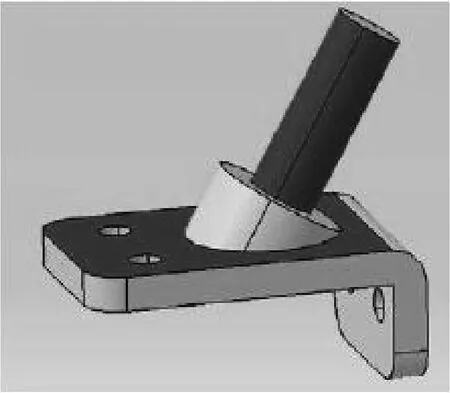
图11 零件特征面选择

表1 最终建造方向集合

表2 不同建造方向下零件整体表面粗糙度

由于计算值为整体零件的平均粗糙度，难以反映零件各个表面的粗糙度情况.为了便于设计人员或者工程师直观了解零件各个表面质量情况，通过嵌入零件粗糙度计算模型程序，开发了表面粗糙度可视化程序，将粗糙度的变换情况直观呈现.可以看到，如图12所示，在不同的建造方向下，零件的不同表面粗糙度将随之变化.

通过一个球面零件来验证该算法的可靠性，如图12所示.该零件包含8 424个点，三角型面片数为2 808个.通过运行自主开发的程序，图像较为直观地反应了整体零件粗糙度的变动情况，可以看到零件的表面质量变化趋势符合之前的综合粗糙度预测模型的预测值.由于球形中部面片的成型角度约为90°，因此表面质量最好，随着三角面片成型角度逐渐远离90°，表明粗糙度逐渐增加.对于上、下半球，可以看到表面质量不是简单地对称，由于上半球不需要支撑，因此表面质量相较于下半球较好，反映了支撑对于零件表面粗糙度的影响.实例证明该程序运行稳定，兼容性强，可运用于大多数零件的STL文件.

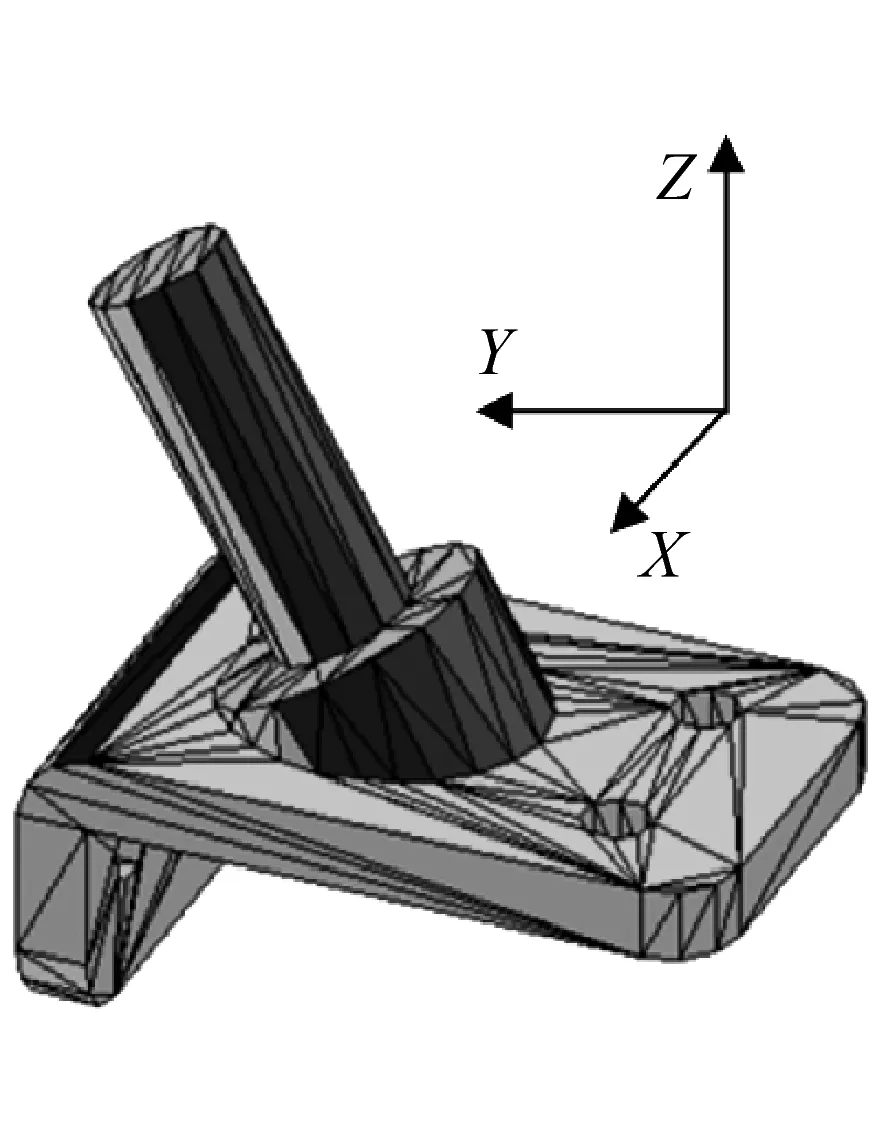
a

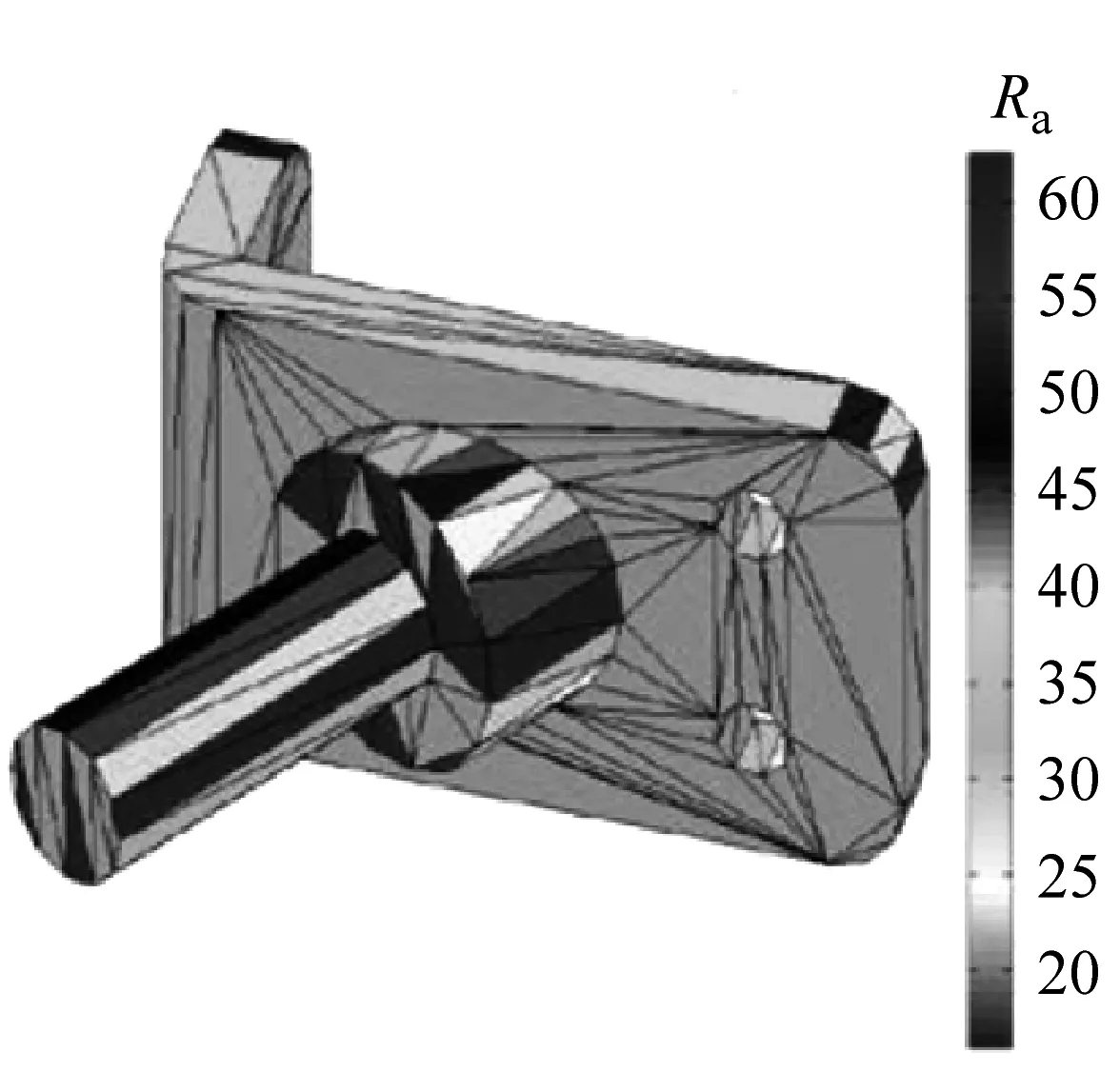
b

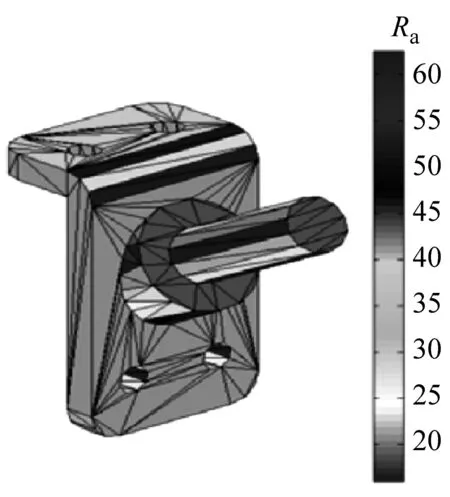
c

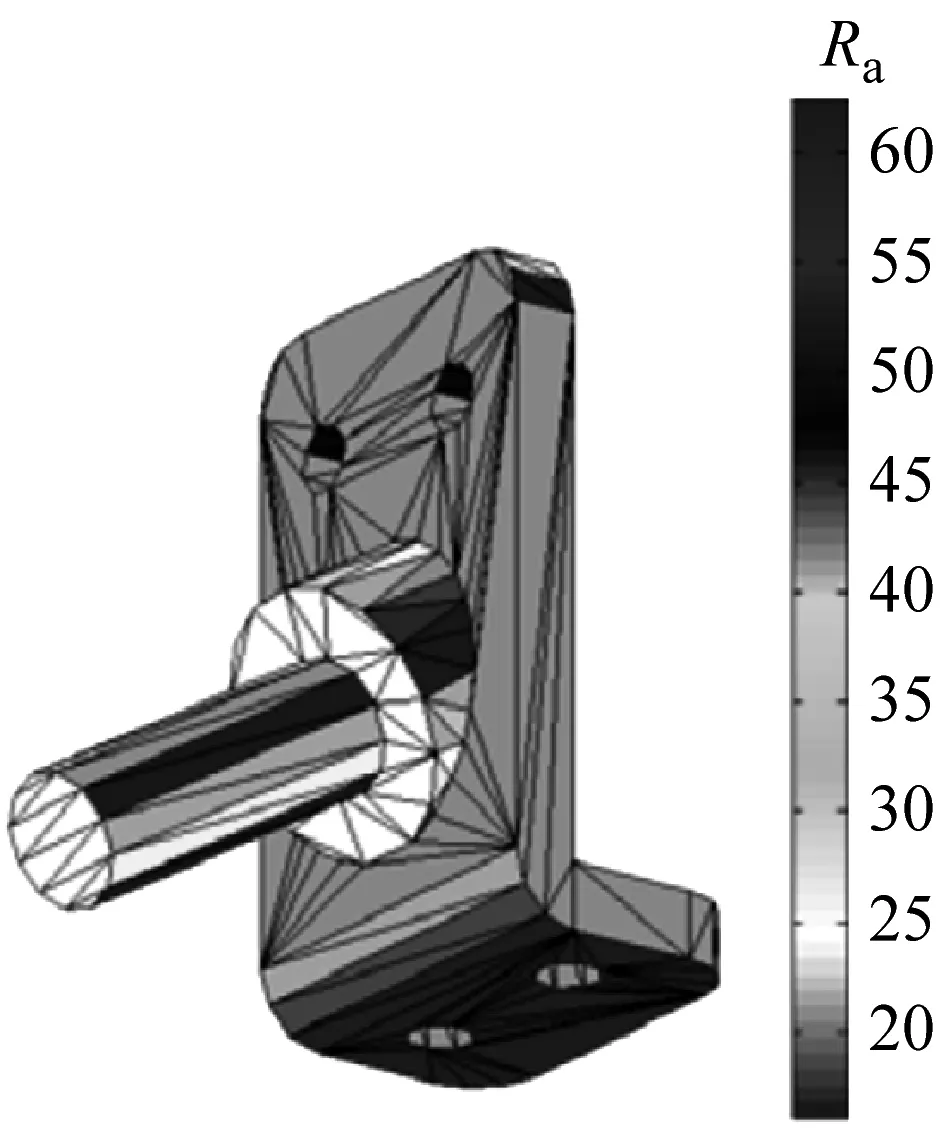
d

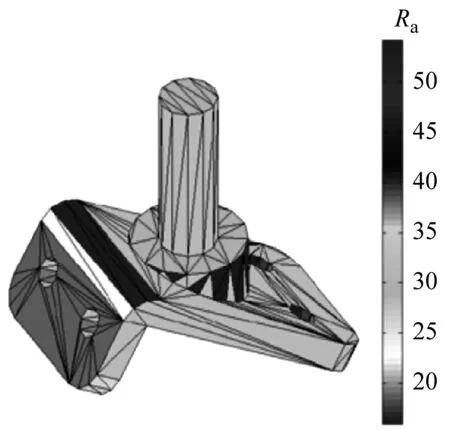
e

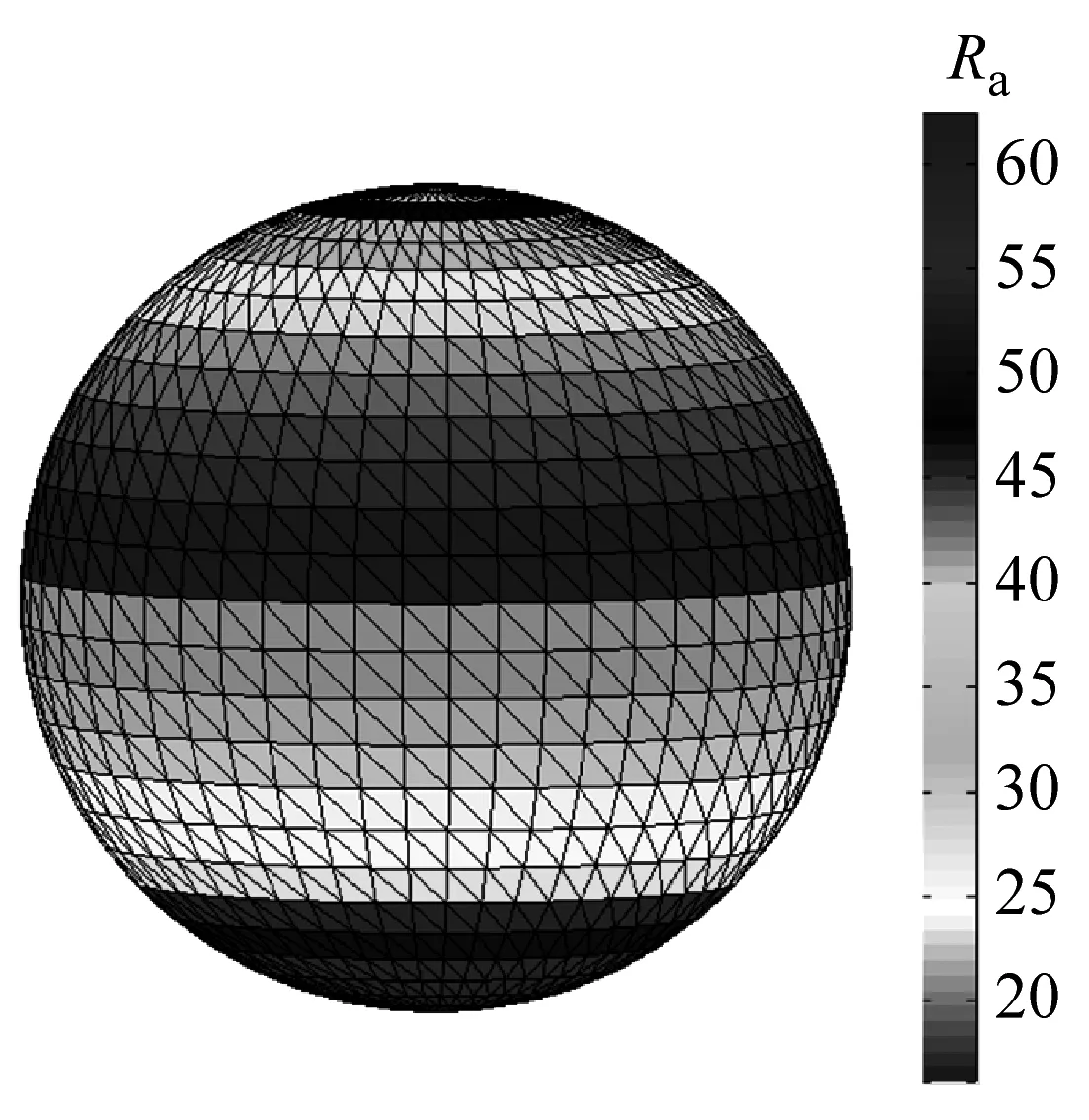
f

3.2 基于支撑面积的建造方向优化

针对上述零件模型，使用基于支撑面积的建造方向优化数学模型，分析支撑面积的大小随模型中参数α和β的变动情况.如图13所示，可以发现，存在两个建造方向，即(α,β)对应于(90°,45°)以及(158°,89°)时使得支撑面积取最小值.

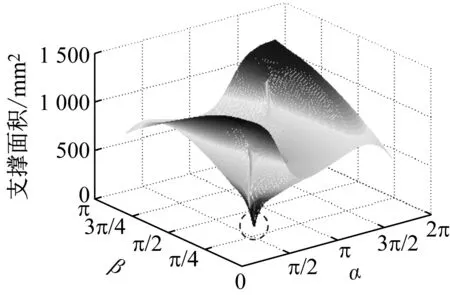
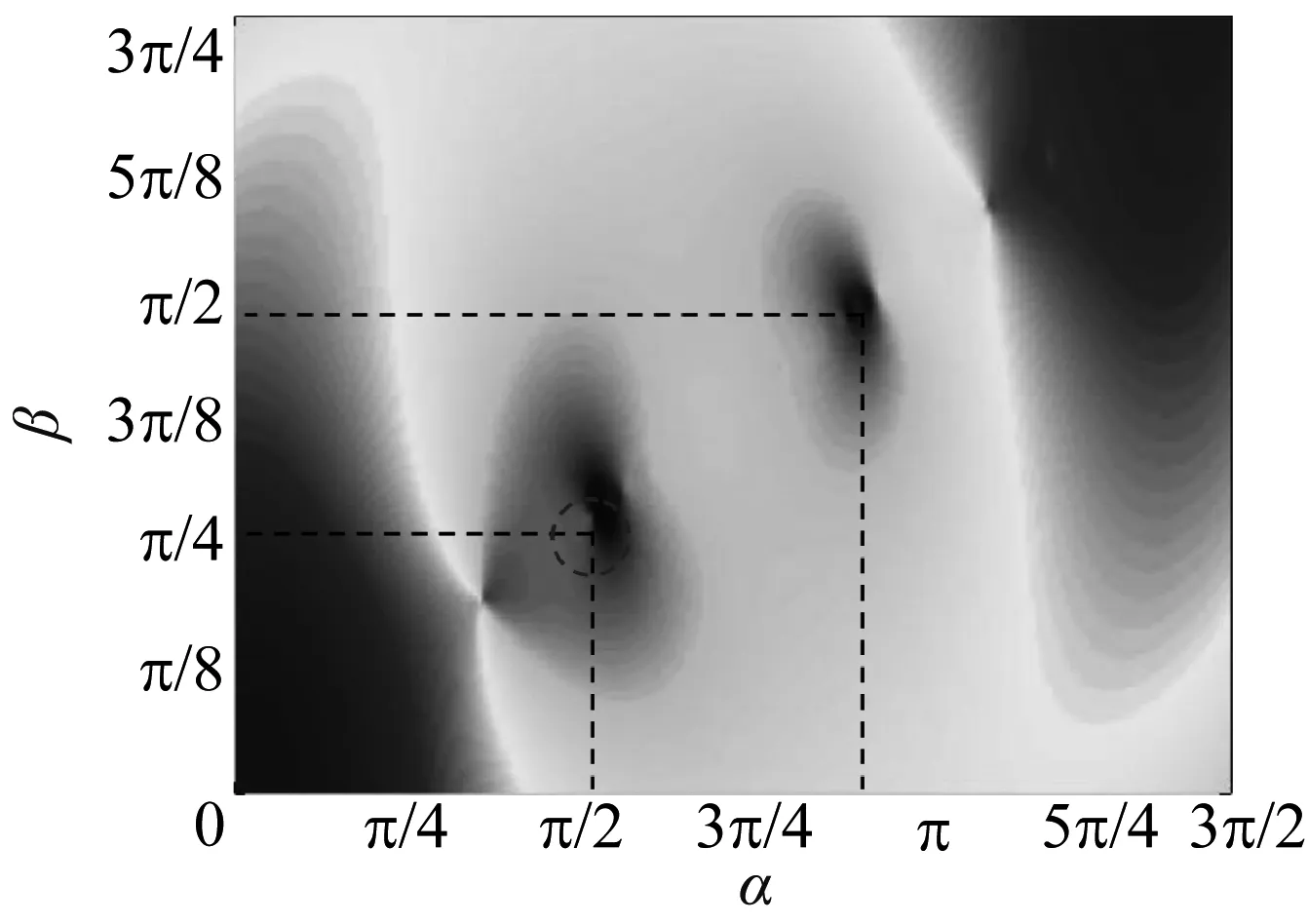
图13 建造方向变化对支撑面积的影响

使用遗传算法，进行以支撑面积为目标的建造方向单目标优化.根据遗传算法结果，如图14所示，从最原始的种群开始，经过100次的遗传迭代，支撑面积趋于稳定，从70代以上收敛于9.242 2，对应Np方向为(0.088 5，0.704 5，0.707 0).通过公式(5)，可得α和β分别为85°和45°，与图13的情况较为一致.

3.3 耦合表面粗糙度和支撑面积的建造方向优化

为直观反映两个性能的耦合情况，将表面粗糙度模型(图15)与支撑面积模型(图13)进行对比(图15中框选出的范围为对应支撑面积与表面粗糙度最低处)，可以看到支撑表面最小和粗糙度最小所对应的α和β存在差异.因此在多目标优化中，需要权衡两者的重要程度.

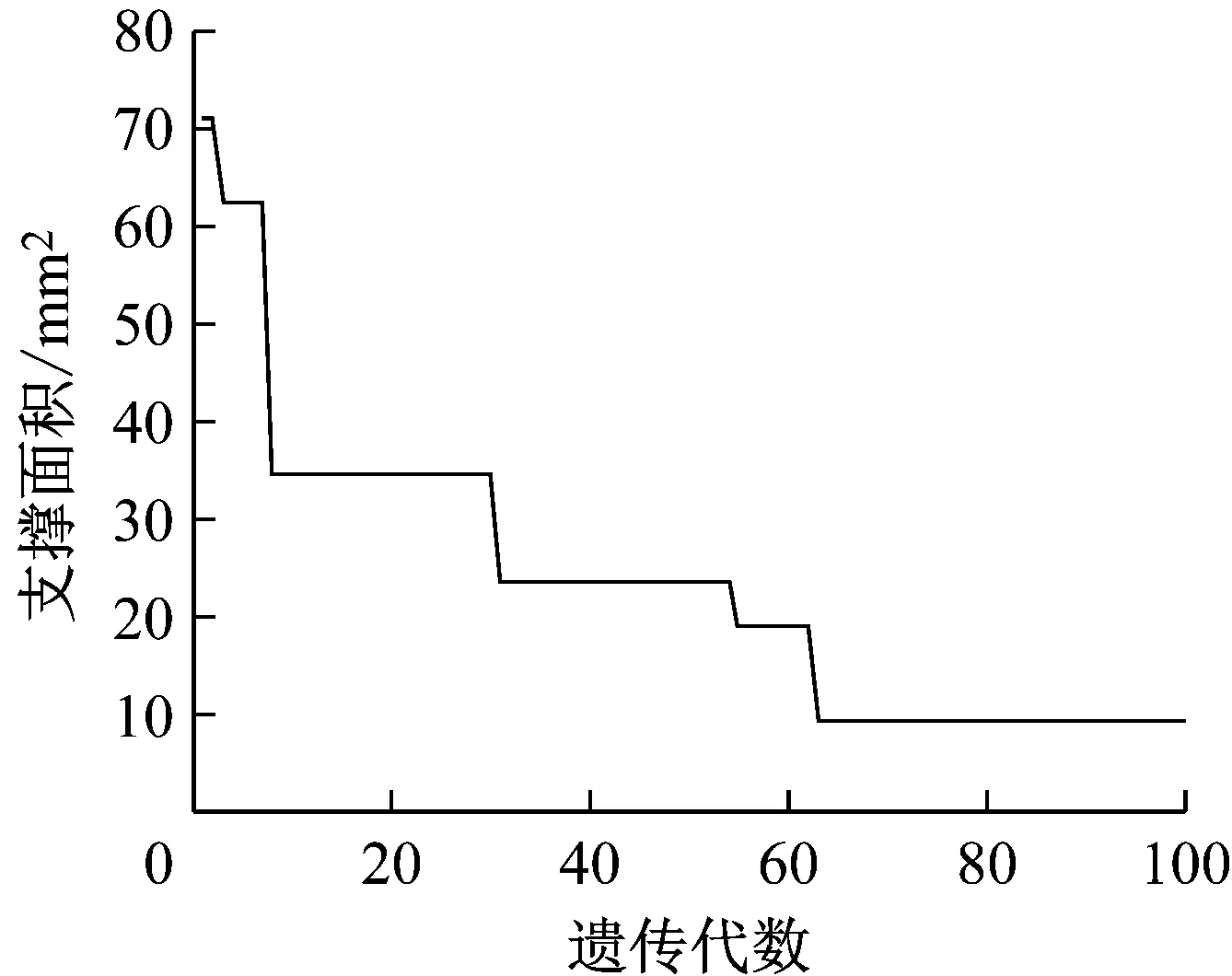
图14 以支撑面积为优化目标的单目标优化遗传算法结果

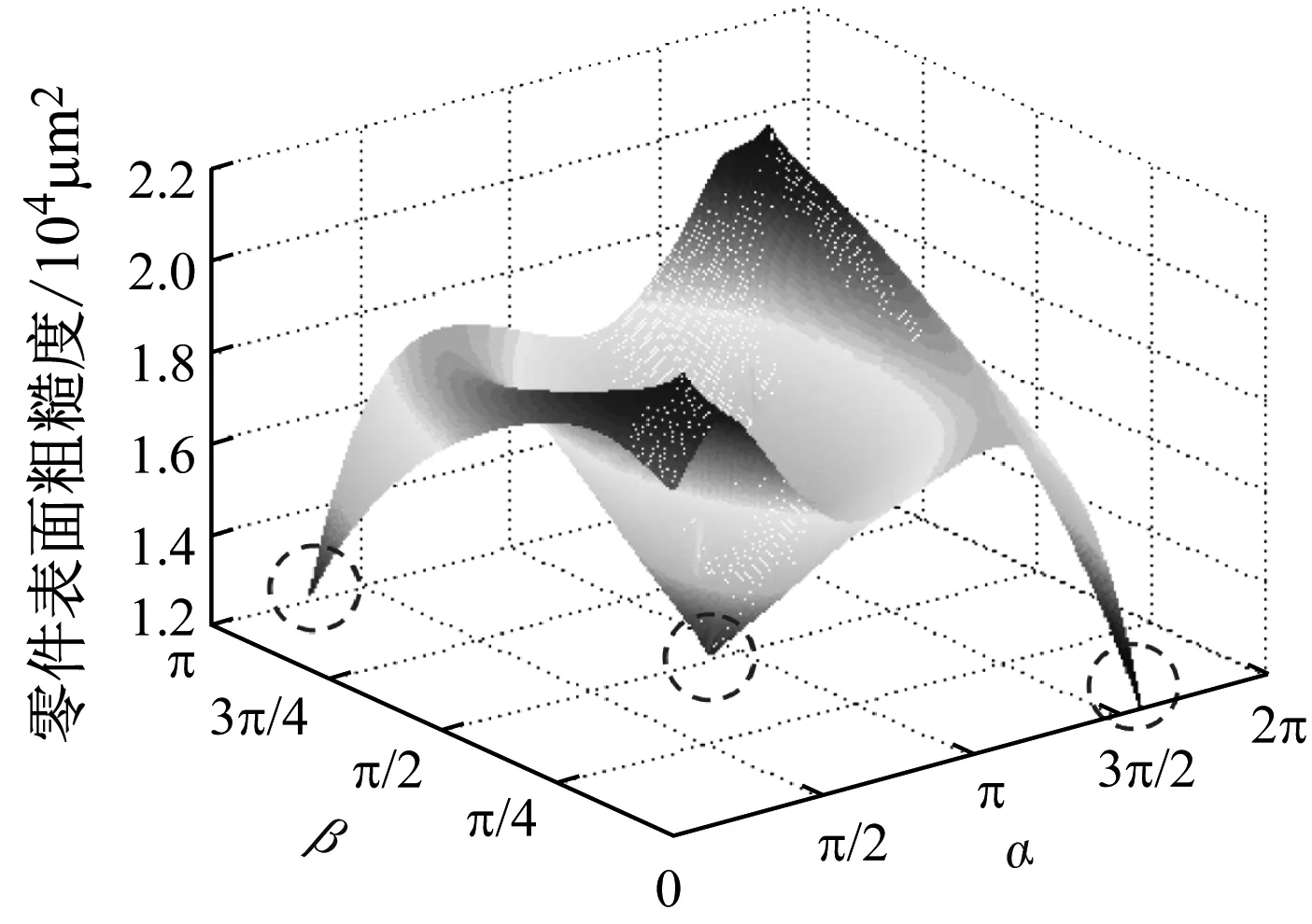
图15 建造方向变化对表面粗糙度的影响

针对上述零件模型，根据多目标优化算法模型，使用MATLAB编写含有权重的表面粗糙度和支撑面积的双目标优化遗传算法.该零件模型有348个三角片面，设置分层厚度0.25 mm.

通过表3所示的优化结果可以看出，在使用有限数量的建造方向集合时，得到的表面粗糙度并不是全局最优的情况.在使用单目标遗传算法进行表面粗糙度优化时，整体的表面粗糙度可以进一步下降，遗传算法通过全局搜索建造方向，使得整体表面粗糙度降为最低.使用单目标遗传算法进行支撑面积优化时，得到的建造方向使支撑面积取得最小值，但是整体表面粗糙度反而恶化，这反映了前文提到的支撑面积和表面粗糙度的性能耦合情况.使用带有权重的多目标遗传算法，最终得到的建造方向使得表面粗糙度接近于全局最小的值，同时支撑面积也在可接受的范围内，实现了双目标同时优化.可以看到，在权重均为0.5的情况下，建造方向趋近于单目标优化粗糙度的情况，这说明，虽然粗糙度及支撑面积对于建造方向的选择处于同等重要地位，同时具有耦合性影响，但粗糙度对建造方向选择的影响程度更大.

表3 遗传算法优化结果

4 结论

本文以 FDM 技术为基础，研究了建造方向对于零件表面粗糙度和零件支撑面积这两个目标的影响，以及制造过程中这两个性能的耦合下的优化.

(1) 在表面粗糙度方面，通过PLA材料制造的Truncheon样件测试不同成型方向下的表面粗糙度，分析了理论模型和实际工况下的差异.结合前人的经验公式，建立了符合实际情况的粗糙度综合预测模型.对于复杂的多面体零件，通过选择功能性表面，得出建造方向集合，并对集合内每个建造方向下的零件整体平均表面粗糙度进行计算，通过对比不同建造方向下的零件平均粗糙度来选择最优的建造方向.

(2) 在零件支撑方面，建立了基于支撑面积的建造方向优化数学模型.使用遗传算法进行单目标优化求解，得到制造过程中支撑面积最小的制造方向，但表面粗糙度反而变大.最后，针对支撑面积和表面粗糙度的耦合问题，将这两个目标联立，建立多目标优化模型，使用遗传算法来寻求全局最优解，实现双目标耦合下的同时优化.

在表面粗糙度方面，实际打印过程中，除了建造方向之外，打印的层厚，速度和冷却温度都会直接或者间接地影响表面质量.在支撑面积方面，影响因素有很多，如冷却温度和打印速度等.包括这些因素的耦合问题等，都是值得未来继续研究的.