基于信息熵的城市道路可变信息板布点方法
衣谢博闻, 唐克双, 李克平
(同济大学 道路与交通工程教育部重点实验室, 上海 201804)
交通诱导系统是智能交通系统(ITS)的重要组成部分,通过对公众发布实时的交通运行信息和出行建议,诱导公众合理选择出行路径,从而有效地缓解交通拥堵,提高交通系统的运行效率[1].可变信息板作为交通诱导系统的主要发布方式之一,以交通标志的形式设置在道路上,通过LED(light emitting diode)屏幕为驾驶员提供动态的诱导信息,因此合理布设可变信息板,确保驾驶员接受诱导信息是交通诱导系统正常运行的基本保证.
目前针对可变信息板布设的研究大都集中于系统层面,研究路网环境下可变信息板的布设密度与布设路段[2-4],尚未有针对单点可变信息板布设位置的研究.而单点交通标志布设位置的研究往往针对传统静态交通标志,对交通标志的前置距离和字体高度进行建模,确保交通标志的合理安装[5-6].20世纪90年代初,李锋[7]提出为了让驾驶员有足够的反应及采取措施的时间,交通标志设置离开特定地点应有合理距离,称为“设置前置距离”.其他学者[7-10]针对交通标志设置位置及影响因素进行了相关研究,发现交通标志前置距离或字体高度选择不合理,可能导致驾驶员无法完成信息获取,或者迫使驾驶员减速以增加视认时间,增加驾驶风险.
以上研究为可变信息板的科学安装奠定了基础,但是仍存在两个局限:一是未考虑可变信息板中动态信息的因素,研究发现可变信息板在文字数量以及图像复杂度上都高于静态交通标志,因此需要更多的视认时间[11-12].二是以上研究未考虑城市交通环境,在城市交通环境下,驾驶员看到可变信息板后的行动距离受到交叉口标线、信号配时等因素的影响.
综上所述,研究可变信息板单点布设问题需要综合考虑可变信息板的视认时间与所安装的交通环境.因此本文首先对驾驶视认过程进行分析,之后通过引入可变信息板信息量-视认时间模型,建立了城市环境下可变信息板前置距离模型和最小字体模型.以上模型可以确保驾驶员有充分的时间接受可变信息板发布的诱导信息,并在接受信息后有充分的反应距离.为可变信息板的安装提供指引,为交通诱导系统的建设提供技术支持.
1 交通标志视认过程分析
可变信息板是交通标志的一种,因此可变信息板的视认过程与交通标志相类似.驾驶行为心理学的研究发现,驾驶员对交通标志的视认过程可分为如下4个阶段,如图1所示.

图1 驾驶员交通标志视认过程
(1) 感觉阶段l1,即驾驶员在视野范围内发现交通标志,直到驾驶员可以看清交通标志位置.感觉阶段驾驶员无法看清交通标示,因此无法对交通标志的内容进行视认.
(2) 视认阶段l2,从驾驶员读取标志内容开始,到完成读取为止.视认距离l2由车辆的行驶速度和驾驶员的视认时间决定,即
l2=vtr
(1)
式中:v为车辆的行驶速度,通常取道路的最高限速vL;tr为可变信息板的视认时间,在以往的研究中取定值2 s[6],但是该定值无法满足可变信息板的视认需求.
(3) 判断阶段l3,从驾驶员完成交通标志内容读取开始,到驾驶员通过对标志提供的信息进行分析、处理、判断并最终做出决定为止,包括脚踩制动及制动生效的时间.判断距离l3取决于判断时间和车速,即
l3=vtth
(2)
式中:v为车辆的行驶速度,为保证驾驶员视认,v的取值为道路最高限速vL;tth为驾驶员的判断时间,通常取值为2 s.
(4) 执行阶段l4,表示从车辆开始反应到完成交通标志所要求的操作,例如减速,停车等需要的最小距离.
交通标志设置位置的选择,即前置距离ls的确定.ls表示交通标志设置点位与交通标志要求驾驶员完成任务点之间的距离.
l5表示驾驶员开始视认交通标志时与交通标志之间的距离.其计算公式为
l5=200hc
(3)
式中:hc为可变信息板上字体高度.
l6表示从驾驶员受到交通标志位置与车辆结构影响导致无法视认交通标志到交通标志之间的距离,即无法视认距离.如图 2所示,交通标志在驾驶员视野存在两个消失点,即水平消失点和垂直消失点.对水平消失点,设d为交通中心到视认车道中心线的距离,水平角β1最大为15°,无法视认距离为l6,h;对垂直消失点,设h为标志上端到驾驶员水平视线即高度1.2 m的距离,垂直视角β2根据交通标志的设置方式分为两种,对于悬臂式和门架式悬空标志一般取8°,路侧柱式标志取15°,无法视认距离为l6,v[13].对l6,h,l6,v取最大值,得出消失点和交通标志之间的距离.

(4)
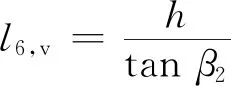
(5)
l6=max{l6,h,l6,v}
(6)
综上所述,交通标志的合理布设需要满足以下两个条件:
(1) 驾驶员有足够的时间用于阅读交通标志的内容,即
l5-l6≥l2
(7)
将公式(3)~(6)带入公式(7),整理后可以得到交通标志字体高度模型为

(8)
其中tr为可变信息板视认时间,其取值应当充分考虑可变信息板的复杂程度及其包含的信息量,确保驾驶员有足够的视认时间.
(2) 驾驶员有足够的距离完成交通标志要求的行动,即
l5+ls≥l2+l3+l4
(9)
其中,l5+ls表示交通标志为驾驶员提供的总视认、判断和行动距离;l2+l3+l4表示驾驶员视认、判断和行动所需要的最小距离.其中l4为必要行动距离,针对可变信息板,必要行动距离应当包含减速距离和变道距离.下文将针对以上两个条件分别进行论述.
2 可变信息板视认时间模型
由上文可知,计算可变信息板视认时间是合理设置可变信息板的关键问题.现有的可变信息板视认时间研究根据建模原理可以分为两类:一类是通过实地试验或实验室模拟实验直接测量具体可变信息板的视认时间,其优点是可以明确得出测试可变信息板需要的视认时间.但是这类方法的通用性较差,需要不断对新型的可变信息板进行补充实验[14-17].另一类方法是找寻中间量表示可变信息板所包含的信息,之后通过实验建立中间量与视认时间的关系模型.例如Dudek和Huchingson提出的信息单元概念,将可变信息板包含的文字拆分成不同信息单元,如时间、地点、事故等,并假设每个信息单元具有相同视认时间,通过实验建立了可变信息板信息单元—视认时间模型[18-21].该类方法具有良好的扩展性,但目前仅适用于纯文字形式可变信息板,无法对包含图形诱导信息的可变信息板进行分析.针对以上缺陷,本文将建立以可变信息板信息量为中间量的可变信息板视认时间模型.
2.1 可变信息板信息量模型
根据信息工程学中信息量的概念,可变信息板信息量可被定义为驾驶员选择期望的改变.因此驾驶员选择期望则可通过熵进行表示,即

(10)
式中:H(X)为驾驶员的选择期望,即熵;p(xi)为驾驶员选择xi的概率,驾驶员的选择概率可以通过实验和调查获取;b通常取值2,此时熵的单位为bit.X为驾驶员的选择集合,根据可变信息板的诱导类型确定.例如:当可变信息板为路径诱导板时,X是驾驶员的路径选择集合;当可变信息板为停车诱导板时,X是驾驶员停车场的选择集合;当可变信息板为限速可变信息板时,X是驾驶员速度选择的集合.
驾驶员接收到可变信息板上的信息后,其选择将会趋于合理和集中,因此期望熵将会减小.期望熵的改变由可变信息板的信息引起,即可变信息板信息量为
I=H0(X)-H1(X)
(11)
式中:I为可变信息板的信息量;H0(X)为驾驶员没有接收诱导信息时的选择期望熵;H1(X)为驾驶员接受诱导信息之后的选择期望熵.
2.2 可变信息板信息量-视认时间模型
基于2.1节提出的可变信息板信息量模型,对上海市杨浦区五角场区域的停车、行车以及停行车一体化诱导板(见图3)进行实验.测量不同诱导板的信息量与视认时间,构建可变信息板信息量-视认时间模型.实验首先在可变信息板诱导范围内选择8个目的地,对应为不同的驾驶任务.8个驾驶任务与4种可变信息板板面可组成32组不同的测试单元,将32组测试单元随机排序,可获得一个测试方案.之后招募实验人员(30人次)分别完成不同的测试方案,即顺序逐个完成测试方案中所包含的测试单元.在单独的测试单元中,首先告知实验人员驾驶任务,在其明确驾驶任务后为测试人员展示可变信息板,并开始计时,直到实验人员确认行车路径后,停止计时并记录实验人员的行车路径.实验可以获得不同可变信息板的视认时间、视认次数以及路径选择数据.将驾驶员路径选择数据带入公式(11)可以得到各类可变信息板的信息量,即4块诱导板针对不同驾驶任务的平均信息量分别为3.89、3.58、4.19和3.62 bit.实验结果表明,提出的信息量模型可以有效区分不同可变信息板之间的复杂程度[22].

a 停车诱导板

b 停行车一体化诱导板

c 停车诱导板附文字诱导

d 停行车一体化诱导板附文字诱导
实验结果显示,驾驶员对于可变信息板的视认时间受到两种因素的显著影响,一是驾驶员对于诱导板的熟悉程度,二是诱导板信息量[16].因此本文采用双层线性模型对可变信息板视认时间、视认次数与信息量进行拟合,拟合模型的结构如下:
第一层模型为
lntr=α0-α1lnxt+r
(12)
第二层模型为

(13)
式(12)、(13)中:tr为可变信息板视认时间;xt为驾驶员对于可变信息板的视认次数;γ00、γ01、γ10、γ11为固定效应;I为信息量;u0为随机效应.第一层模型为学习曲线模型,表达驾驶员熟悉程度对于视认时间的影响;第二层模型为信息量模型,表达信息量对于视认时间的影响.拟合结果如表1所示.
最终得到的信息量与视认时间的拟合模型为

表1 模型拟合结果
tr=exp(1.52-0.11I+
(-0.54+0.08I)lnxt)
(14)
由式(14)可知,视认时间tr随视认次数xt增大而减小.因此当视认次数xt取最小值1时,视认时间tr为最大值.将公式(14)带入公式(8),最终得到基于可变信息板信息量的字体高度的计算公式为

(-0.54+0.08I)lnxt)v+

(15)
在计算最不利情况时,xt应取值1.
3 城市环境下行动距离计算
3.1 最小行动距离计算
可变信息板具有路径指引功能,因此驾驶员的行动内容应当包含变道行为和减速行为,即
l4=lch+lde
(16)
式中:l4为车辆根据诱导信息完成相应交通任务需要的最小距离;lch为车辆变道需求距离;lde为车辆减速需求距离.汽车变换车道是一个复杂的行驶过程,车流密度、行驶速度和道路条件都会对变道产生影响.为保证lch计算结果有效,需要选取最不利情况进行考虑,即最长变换车道距离.
lch=(nlanes-1)Lch
(17)
式中:nlanes为道路车道数;Lch为车辆单次变道需要的距离,该距离发生在超越相邻车道上的汽车后变换到该车道的过程中.具体计算如下:

(18)
式中:v1为超车速度,取路段最高限速vL;Tch为变换1次车道的时间,s,取6.2~6.9 s[23].
公式(16)中减速距离lde的计算如下:

(19)
式中:vi为车辆的初速度;vo为行动完成后的车速;a为车辆减速度.按照最不利情况取值,车辆初速度为道路最高限速vL,车辆行动完成后速度为0 km·h-1.
3.2 可用行动距离计算
城市交通环境下可变信息板布设位置如图4所示.
由图4可知,可变信息板前置距离ls可表达为
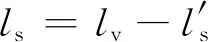
(20)

(1) 排队长度大于不可变道距离,如图4a所示,此时不可行动距离为最长排队距离lq.
(2) 排队长度小于不可变道距离,如图4b所示,此时车辆在进入不可变道路段后仍可以进行减速行为,因此需要在不可变道距离中去除减速距离.
综上所述,受限制距离为

(21)
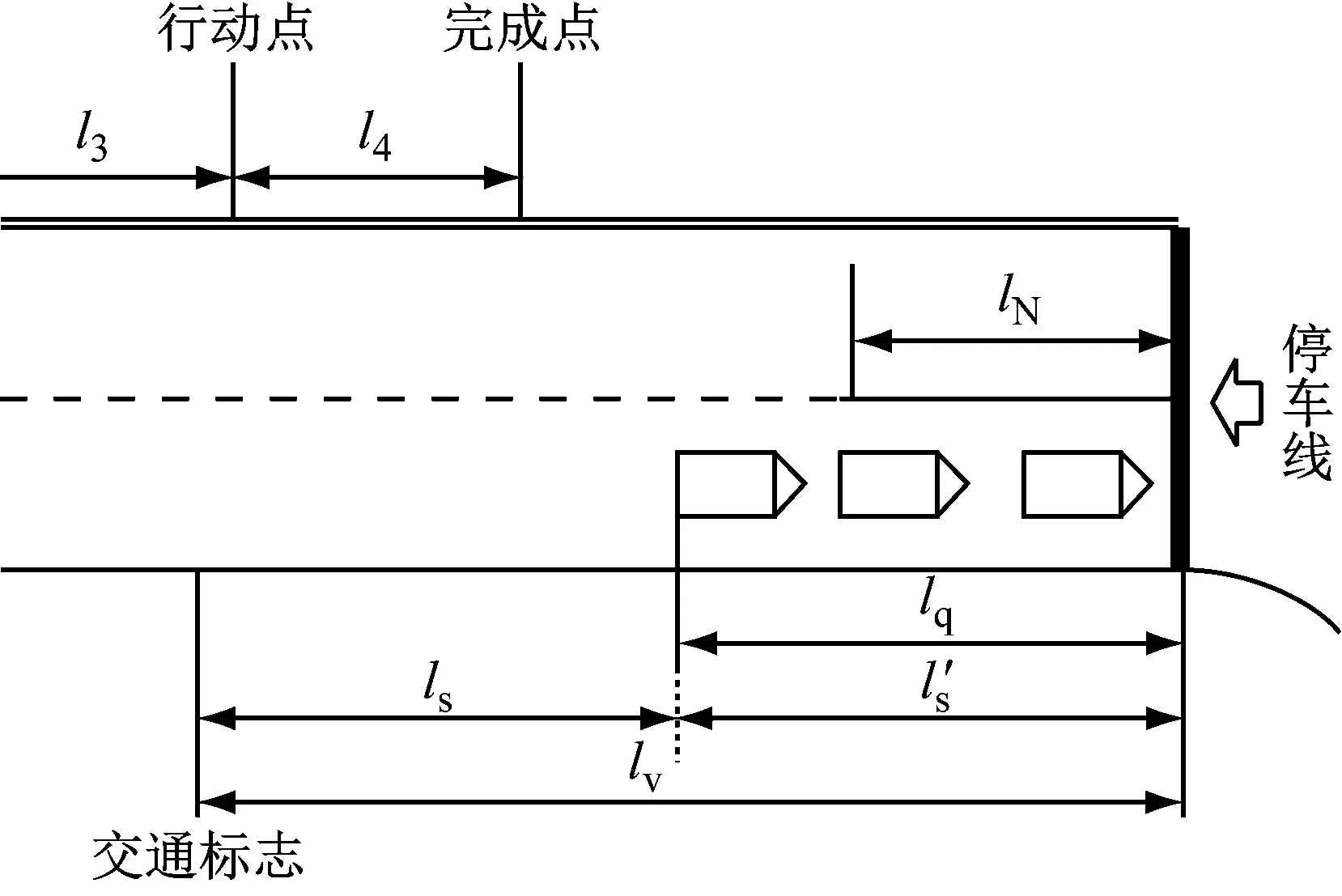
a 排队距离大于不可变道距离

b 排队距离小于不可变道距离
式中:lq为排队距离;lde为减速距离;lN为不可变道距离;lg为不可变道距离与排队距离之间的差值,即
lg=lN-lq
(22)
其中交叉口排队距离lq可以通过实地调查和公式计算两种方法获取.排队距离公式计算分为两种情况,即拥堵情况(有效绿灯时间内无法清空所有排队车辆),和非拥堵状态(绿灯时间可以将排队车辆全部清空).在拥堵情况下,进口道排队长度随时间增加而不断增加,此状态本文不做讨论.在非拥堵情况下车辆排队长度为红灯时间内到达车辆数,即

(23)
lq=max{lq,k}
(24)
式中:lq,k为第k个绿灯相位对应的最大排队长度;nlanes,k为第k个绿灯相位对应的排队车道数;Lq为排队车辆的平均车头间距;C为交叉口的信号总周期时长;uk为第k个绿灯相位的有效绿灯时间;lq为最大排队长度.在实际计算中也可以根据HCM2010中的调查方法,取95%分位排队长度做lq.
综上所述,将以上公式带入公式(9),整理后获得可变信息板安装位置计算公式为
lv≥vL(tr+tth)+(nlanes-1)Lch+

(25)
4 模型应用与分析
城市可变信息板布点模型可以应用于:①对已建成的可变信息板检验;②为拟建的可变信息板提供设计参考.
4.1 已建可变信息板检验
对于已建成可变信息板的评价主要分为两部分:①可变信息板字体高度是否满足视认需求;②可变信息板前置距离是否能为驾驶员提供足够的行动距离.
本算例研究的可变信息板为一块一级停车、行车一体化诱导板,位于上海市杨浦区国定路由南至北段.该诱导板的具体位置与样式如图 5所示.根据实际调查得到可变信息板所在路段的限速为40 km·h-1,可变信息板北段道路为两车道,南段道路为单车道.可变信息板为悬臂式,离地高度为4.50 m.信息板宽度为3.12 m,字体高度为0.30 m.已建可变信息板检验过程如下:

图5 可变信息板
(1) 字体高度检验
字体高度检验即判断可变信息板提供的可视认距离是否满足可变信息板需要的视认距离.
可变信息板可视认距离计算:可变信息板的可是视认距离为可变信息板最大可视认距离减去不可视认距离,如公式(7)所示.其中最大可视认距离由可变信息板字体高度决定,根据公式(3)计算,即l5=200hc=200×0.3 m=60 m.由于可变信息板距离上游交叉口小于60 m,因此可变信息板最大视认距离取到达上游交叉口距离,即最大可视认距离为57.00 m.可变信息板的不可视认距离由公式(4)、(5)、(6)求得.通过计算得到水平可变信息板不可视认距离为18.66 m,垂直不可视认距离为11.18 m,即可变信息板在驾驶员视野中消失距离为可变信息板前18.66 m.最终根据公式(7),得到可变信息板的可视认距离为38.34 m.

此时,可变信息板提供的可视认距离(38.34 m)大于该可变信息板视认距离需求(34.56 m).因此该可变信息板字体高度设置满足视认需求,可以为驾驶员提供足够的视认时间.
(2) 前置距离检验
前置距离检验即判断可变信息板是否为驾驶员提供充足的可行动距离.
可行动距离计算:可变信息板可行动距离为可变信息板消失点到交叉口停车线之间的距离,减去驾驶员判断距离与限制行动距离.本算例中,可变信息板视认消失点与布设点之间的距离为18.66 m,可变信息板布设点与交叉口停车线之间的距离为32.00 m,因此可变信息板消失点到交叉口距离为40.66 m.驾驶员判断距离可根据公式(2)计算得到,即l3=vtth=22.22 m.限制行动距离由交叉口不可变道距离和排队距离共同决定.本算例中,可变信息板设置的进口道仅有一条车道,无不可变道距离.排队距离通过实地调查获得为10 m(对于无法调查的可变信息板,可以根据公式(23)和公式(24),即限制行动距离为10.00 m.最终得到可行动距离为40.66 m-22.22 m-10.00 m=8.44 m.
行动需求距离计算:行动需求距离即最小行动距离,由最小变道距离与减速距离组成.由于本算例为单车道,不涉及变道需求,因此最小行动距离即减速距离,根据公式(19)得到最小行动距离为7.71 m.
此时,算例可变信息板提供的可行动距离(8.44 m)大于最小行动距离(8.44 m).因此该可变信息板的设置满足行动需求.
4.2 拟建可变信息板设计推荐值


表2 可变信息板布设推荐值
注:*为不提供具体建议值.
从表2可以发现:①本文模型得到的推荐字体高度均大于规范推荐的最小字体高度.更大的字体高度,可以为驾驶员提供更长的视认距离和视认时间,从而确保驾驶员对可变信息板的有效视认.②本文模型得到的推荐字体高度随车道数的增加而增高,以确保内侧车道驾驶员的有效视认.③规范给出的推荐前置距离易于实际操作,而本文模型给出的推荐前置距离综合了更多影响因素,以应对城市区域复杂的交通环境,更具指导意义.
5 结论
本文从交通标志视认过程的分析入手,针对可变信息板信息量大以及城市交叉口的布设环境,引入了可变信息板信息量模型,并建立了基于信息量的城市可变信息板最小前置距离和字体高度模型.该模型可用于对已建成可变信息板进行校验,或为设计阶段的可变信息板设置提供指导.最后通过对比本文计算的建议值与国家标准给出的推荐值,发现本文提出的算法更符合城市路网环境复杂以及可变信息板信息量大的特性.对现有可变信息板的设计标准进行了补充.

