基于红外遮蔽的地面烟幕防空阵地部署模型研究

曾照凯， 朱东升， 郭潇迪， 王丁， 高晓辉

(1.军事科学院 防化研究院, 北京 102205; 2.中国人民武装警察部队研究院 装备技术研究所, 北京 100012)

0 引言

随着光电技术的发展，现代战争中光电制导对战场重要目标的生存构成了极大威胁[1]。而烟幕在对抗红外制导、激光制导、毫米波探测等光电武器方面具有显著成效[2-3]，尤其是对探测灵敏度高、抗干扰能力强、空间分辨率高、能自动识别远程小目标和多目标并选择命中点的高精度红外末制导武器(应用红外成像制导技术)，可实现有效干扰[4]；加之近年来在烟幕干扰材料[5]、烟幕干扰效果[4]、烟幕干扰技术[6]等方面的深入研究，其防空作战效能日益凸显[7]，因此高效费比[8-9]的烟幕干扰手段也得到各国军队的普遍重视[10]。然而，现有各型发烟装备在实际作战中缺乏科学的决策手段，难以快速、有效地形成空间遮障，大大降低了烟幕的防空效能，亟待建立辅助决策模型，以实现发烟的科学决策。对此，朱安国等[11]研究了目标预测、阵地配置、防空预警、建立空间遮障、火力分配等辅助决策模型，通过空中爆炸发烟弹施放烟幕实现了对光电侦察与光电制导的干扰。基于此，需要继续研究地面发烟装备的作战辅助决策模型，以配合空中烟幕施放，为未来形成空地一体立体化烟幕奠定基础。

发烟车、发烟罐等地面施放烟幕的发烟装备[9]，与发烟弹相比具有成烟量大、持续时间长、效费比高的优点，合理配置地面发烟装备以充分发挥其作战效能，并配合空中烟幕弹、形成空地一体立体化烟幕墙，是烟幕防空作战研究的重要方向。当敌主攻方向与风向垂直或夹角较大时，采用多点顺风发烟装备配置方式[12]，在保障目标与空袭武器之间形成一道垂直地面且与地面相连的烟幕墙，可达到干扰光电制导的目的，实现对保障目标特定方位的对空防御；而如何部署发烟点、形成所需的烟幕墙成为解决问题的关键。为此，本文基于红外遮蔽烟幕对抗末制导，探索构建地面发烟装备预先阵地部署模型，以期为未来防御激光、毫米波等其他光电武器的相关模型构建研究奠定基础。

1 烟幕扩散模式

获得烟幕在大气扩散作用下的浓度分布是评估发烟器材效能及研究烟幕使用的基础，而可预测烟幕时空分布的烟幕扩散模式必然成为烟幕防空领域研究的重点[13]。烟幕扩散模式可区分为解析解模式与数值模式，就本文研究的连续扩散点源——发烟车、发烟罐而言，发展较为成熟的扩散模式为：1)数值模式的代表——随机游走粒子模式，在复杂地形、风场和湍流场中可较为精确地模拟烟幕的时空分布，但模拟速度较慢，无法满足烟幕防空的时间要求；2)解析解模式的代表——高斯模式，输入参数少、表达式简单，便于各物理量之间关系的分析和数学推导，计算速度快且具有相当的预测精度。姚禄玖等[13]认为，在辅助发烟装备设计与评价时，需采用精度较高的模式，而在试验场辅助设计或烟幕应用计算时，可采用较为简单的模式。因此，解析解模式适用于战场烟幕使用的实时计算与预测。

高斯假设理论认为，连续独立随机变量和的概率密度函数随其数量趋于无穷大而趋向于高斯分布，即使烟幕的瞬时空间浓度非高斯分布，但在一个远比拉格朗日积分时间长的时段内求解的平均浓度也会具有高斯分布的形式。美军于1987年10月和11月在印第安纳州中南部艾登堡预备役空军训练中心(ARFTC)开展了“艾登堡-87雾油和六氯乙烷(HC)烟幕野外研究”，研究过程及结论在美国AD报告(AD-A212983)中有详细描述。该项研究证明了雾油烟幕的粒径分布符合对数正态分布，98的烟幕粒径D在0.3～3.0 μm间，其烟幕粒径D与红外遮蔽烟幕粒径均小于15 μm. 故在相同环境条件下的扩散规律符合相同的高斯模式，即雾油烟幕可理想地看作是红外遮蔽烟幕中的一员。另外，该项研究基于单点烟幕施放，于下风向预设了5个垂直风向的横截面，并将每个横截面2 m高度处采集的雾油浓度数据分布与高斯烟羽模型解算的浓度数据分布相对比，从而确认高斯烟羽模型在下风距离较小(≤250 m)时显示出与试验数据较好的一致性。由于烟幕防空作战对时间要求很高，单点所需遮蔽的区域于下风向的距离必在250 m范围内。综合上述分析可知，高斯烟羽模式应用于防空作战中战场红外遮蔽烟幕的实时计算具有科学性。

于是，在较稳定、均匀的气象条件(有风情况下烟轴高度的平均风速u≥1.5 m/s)下，若以红外遮蔽烟幕(D<15 μm)施放点的地面投影为原点建立空间直角坐标系，则其浓度分布服从如下高斯烟羽模型：

(1)

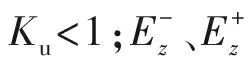
同时，根据烟幕遮蔽质量[14]的定义有，如下烟幕遮蔽基本方程：

(2)

式中：mb为烟幕遮蔽质量(g/m2)；lp为下风距离(m)；Clp为烟幕面密度(g/m2)；Lp=Lp2-Lp1为辐射通过烟幕的光程(m)，Lp1、Lp2分别为光程微积分的下限、上限；C(lp)为烟幕在下风任意位置的浓度分布方程；Clp=mb指烟幕可实现恰好遮蔽。

(2)式为烟幕使用计算中最基本的数学原理与依据，是一切复杂烟幕使用样式计算的理论基础。

本文考虑单点施放垂直烟幕、实现对空防御，即应用单个或多个发烟车、发烟罐形成一个较大源强的连续扩散点源，基于烟幕在下风向的水平、垂直扩散形成烟墙；基于高斯烟羽模型，以烟幕遮蔽基本方程为理论基础，运用数值方法研究单点施放垂直烟幕计算模型，并应用于多点顺风施放垂直烟幕计算模型的研究中；最终构建起多点顺风配置的烟幕防空阵地部署计算模型。

2 垂直烟幕空间尺度计算模型

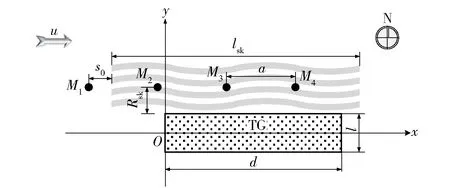
图1 发烟装备阵地部署示意图Fig.1 Schematic diagram of smoke equipment position disposition

多点顺风配置发烟装备是在一条平行风向的发烟线上，每隔一定距离布设一个发烟点并同时施放，以构成首尾相连的有效遮蔽烟幕，如图1所示。考虑到防空作战对成烟时间t有很高要求，等源强配置方式不易有效地控制成烟时间，因此本文采用等间隔配置方式来配置发烟点。

图1中：TG为等效保障目标，即基于风向和保障目标(规则或不规则目标)外形特点所构建的轴向平行于风向且能包含原目标的最小长方体。以TG上风向边缘线中点的地面投影为原点建立空间直角坐标系Oxyz；M1、M2、M3、M4为布设的发烟点；s0为发烟点M1与垂直烟幕墙的距离(m)；a为发烟点配置间距(m)；lsk为烟幕墙最小长度(m)；Rsk为保障目标沿垂直风向与发烟线的最短距离(m)；l、d分别为保障目标的长度(m)与宽度(m)。计算获得有效遮蔽烟幕墙的特征参数及位置参数，是发烟装备阵地配置的前提。

2.1 基本模型构建

当武器来袭方位恰好与风向呈90°夹角时，于保障目标侧面以图1方式布设发烟点成烟，实现有效的烟幕遮蔽，即形成图2所示的烟墙Sk1Sk2，保证来袭目标于成烟距离处Em1至极限距离处Em2之间寻的制导时不能发现保障目标TG. 为了解算方便，本文引入3个概念：1)成烟距离Rs，表示来袭目标进入末端制导阶段时与保障目标的距离(m)；2)成烟时间t，表示防空预警至空袭目标到达成烟距离处的时间(s)；3)极限距离Re，表示来袭目标发现保障目标但无法调整飞行姿态时距保障目标的距离(m)；三者均可基于空袭目标预测获得。

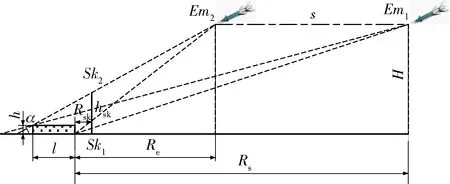
图2 烟幕对空防御示意图Fig.2 Smoke air defense diagram

图2中，α为来袭目标到达极限处与保障目标连线对地面的夹角；h为保障目标的高度(m)；s为来袭目标的战斗航程(m)；H为来袭目标飞行高度(m)；hsk为烟墙最小高度(m)；Rsk越小，hsk越小，烟幕的遮蔽效能越好；同时考虑到烟墙的厚度较大，应保证自由空间中烟幕粒子尽可能多地集中于保障目标一侧，故Rsk取值应适中：发烟车，可取RskWe2(We为该型发烟车的红外干扰烟幕宽度，装备性能参数)；发烟罐采用单点多罐布设时的源强一般也弱于发烟车，可取Rsk(Qe/Qt)·(Wt/2)(Qe为发烟车红外干扰烟幕标准源强，即形成We烟幕宽度所对应的源强；Qt为该型红外干扰发烟罐标准发烟源强；Wt为该型发烟罐的烟幕宽度；三者均为装备性能参数)。基于解析几何分析可计算lsk与hsk：

lsk=d，

(3)

(4)

式中：tanαH-hl+Re，由来袭目标性能H、Re决定，当空袭武器无法预测时，tanα应基于数据库中空袭武器参数取最大值；RAl+Rsk，表示沿防御方向保障目标距发烟线最大距离(m)。

2.2 计算模型修正

在无防御依托条件下的实际作战中，一般将防御空域划分为8个等界方位[15]，每个方位跨度为45°. 如图3所示，当防御方向与风向之间的方位夹角θ<90°时，需要基于夹角θ对hsk和lsk进行修正。

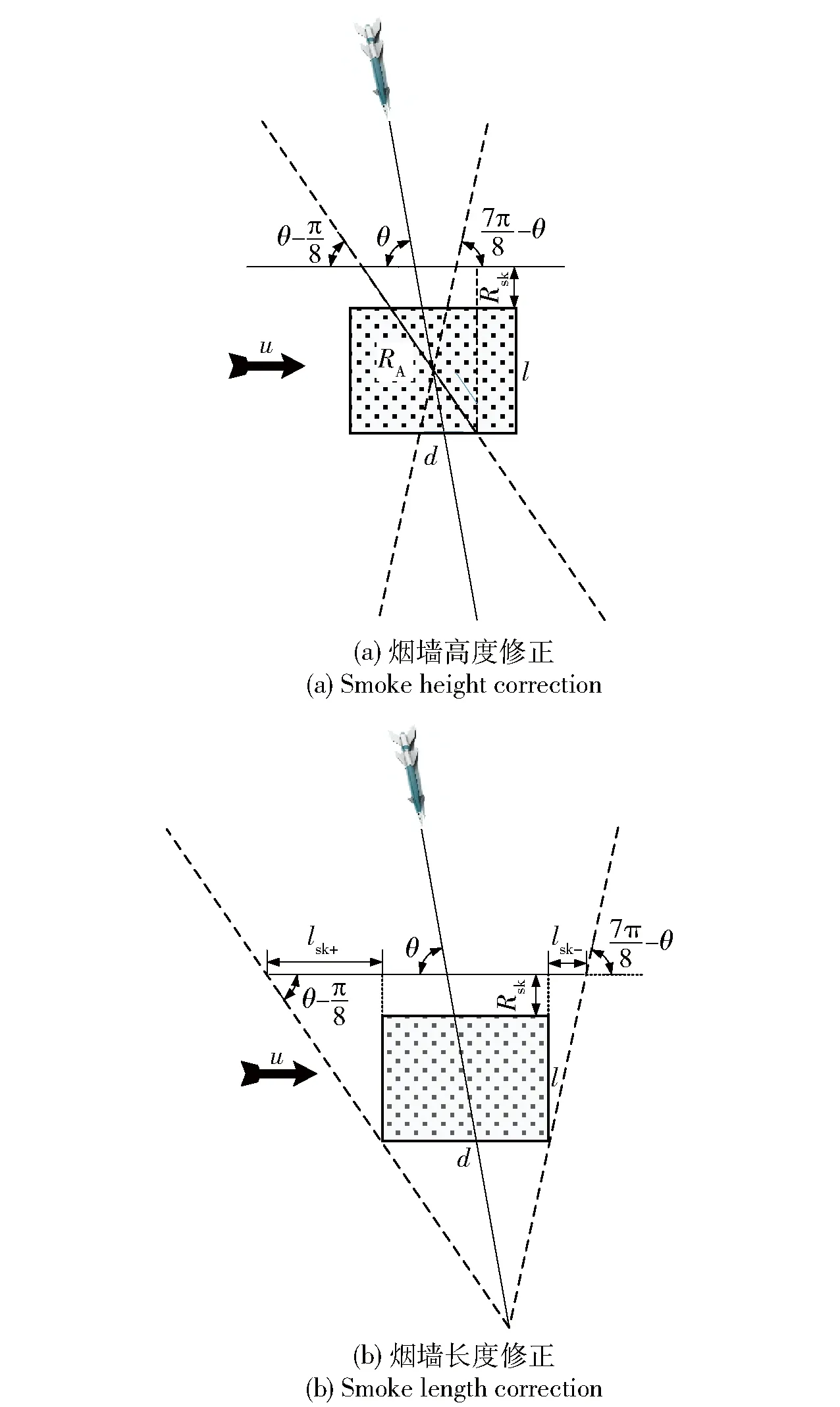
图3 烟幕对空防御俯视图Fig.3 Vertical view of smoke air defense

图3(a)中hsk的修正需要基于参数RA的修正：

(5)

图3(b)中lsk的修正需要基于lsk+、lsk-进行：

(6)

式中：lsk+=l+Rsktan5π8-θ；lsk-l+Rsktanθ-3π8。

总之，运用上述模型可得到所需烟幕的最小空间遮障及其位置。垂直烟墙的上风向起始坐标为(-lsk+,Rsk+l2，发烟点M1的坐标为(-lsk+-s0,Rsk+l2。

3 单点施放垂直烟幕计算模型

垂直烟墙由单个点源或多个顺风配置点源同时发烟、首尾相接而成，计算单个点源所成烟幕的浓度、面密度及效应尺寸等是发烟装备作战使用的最基础性工作[13]。本节以发烟点为坐标原点构建空间坐标系O′x′y′z′，研究单点施放成烟问题。

3.1 遮蔽方程的建立

保障目标具有一定高度h，烟幕于侧面的扩散规律较为复杂，可做如下假设：在坐标系Oxyz下观察，空间{(x,y,z)|x[0,d],y[l2,∞),z[0,h]}内烟幕存在镜面反射，其他空间为自由空间；不考虑保障目标高度h对保障目标正上方烟幕浓度的影响。

自由空间内烟幕浓度服从高斯烟羽模型，而镜面空间需修正为

(7)

两个浓度式所处坐标系与坐标系O′x′y′z′重叠，在坐标系O′x′y′z下解算时，可沿y′轴方向积分两个浓度式，均得到水平遮蔽方程为

(8)

式中：面密度Clp与源强Q呈正相关。只有保证Clpx′,z′≥mb时，才能实现烟幕的遮蔽。

3.2 计算模型构建

首先，当Clpx′,z′mb时，可达到恰好遮蔽。分别取He=0 m、He≠0 m作图4，曲线与坐标轴的封闭区域为可遮蔽区域。图4中，x′F、x′E分别为取He=0 m和He≠0 m达到最大遮蔽高度z′h0、z′hn时所对应的坐标；x′B(用x′V)、x′A(及x′P)分别为取He=0 m和He≠0 m于hsk高度达到恰好遮蔽时所对应的横坐标；x′m、x′M分别为取He=0 m和He≠0 m时烟幕最大遮蔽长度。

图4 单点施放烟幕水平遮蔽示意图Fig.4 Screening based on sing shot smoke laying

当Clp(x′,z′)=mb、He=0 m时：取z′x′的导数等于0，可解得

(9)

取z′(x′)=0可得

(10)

式中：x′m为烟幕最大遮蔽长度。

当He≠0 m时，由于He较小，空间烟幕浓度发生了较小变化。面密度函数Clp(x′,z′)对z′求偏导可得

(11)

在z′ ≥He时，必有∂Clp∂z′<0.

在实际作战中，He较小，相比于hsk几乎可忽略，故结合偏导方程可知：z′=hsk高度处的烟幕水平遮蔽能力可以代表烟墙的最小遮蔽能力。于是，图4阴影区域可表示为单点源施放烟幕形成的有效烟墙，烟墙有效长度为|AP|，且有x′As0. 结合图4与(8)式分析可知：s0取值过小会造成发烟点源强过大或在有限源强下达不到所需烟幕高度，s0取值过大又会使得在成烟时间t内可能无法形成有效遮蔽烟幕。综合考虑，取s0初值为s0=smax/2. 其中，smax为成烟时间内有效遮蔽烟幕沿风向到达的最远距离(m)。假设烟幕沿风向扩散到达之处即形成有效遮蔽烟幕，可取smax=u×(t-tr)，tr为装备发烟准备时间(s)，该式可基于试验进一步优化。

取z′=hskhn，建立关系式：

Δmb(x′)=mb-Clp(x′;z′=hsk)，

(12)

并作图5，研究水平遮蔽质量沿x′轴的变化规律，其中x′W为hsk高度处达到最大面密度时所对应的横坐标。图5与图4的相关点存在一一对应关系。

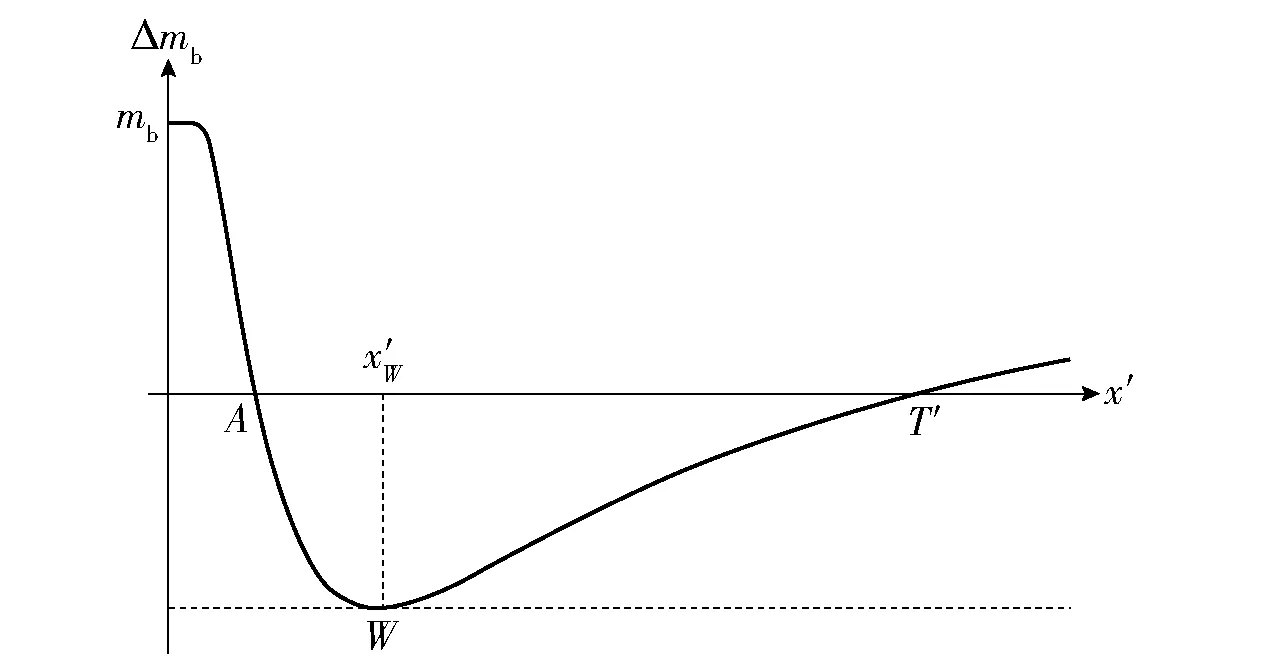
图5 hsk处面密度Clp变化曲线Fig.5 Changing curve of Clp at hsk

1) 取f(x′)=Δmb(x′)，有

(13)

2)对f(x′)求导，有

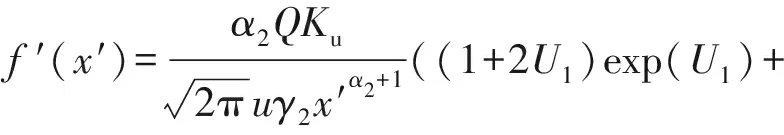
(14)

式中：U1-(hsk-He)2-(hsk+He)2有如下判断：

(15)

(16)

f′(x′=x′m)>0,

(17)

得证。

由此可得到如下单点源施放垂直烟幕计算模型：①基于(12)式，求解取x′=x′A=s0、Clp=mb时的发烟源强Q=Qp，Qp为Q的求解值；②在Q=Qp基础上，以x′m为初值采用数值计算方法(见3.3节)迭代求解x′P；③取lsk0=x′P-x′A，得到单点源施放烟幕有效遮蔽长度。

3.3 计算模型求解

基于Qp、x′m，采用牛顿下山法[16]，可求解x′P.

步骤1准备。选定初始近似值x0x′m，计算f0=f(x′x0)，并取λ1.

步骤2迭代。计算f′0=f′(x′x0)，按(18)式迭代一次，得到新的近似值x1，并计算f1=f(x′x1)。

(18)

步骤3控制。若|f0|≤|f1|，则取λ=λ2，返回步骤2再次解算。否则，继续判断：若|f1|ε(ε为允许误差)，则x′P=x1即为解算结果；否则执行步骤4.

步骤4修改。若迭代次数达到某指定次数n，则终止计算；否则取λ1，f0=f1，x0=x1，返回步骤2继续迭代。

获得x′P后，取lsk0x′P-x′A，即可得到单点源施放烟幕有效遮蔽长度。

4 烟幕防空阵地部署计算模型

烟幕防空阵地部署计算模型是结合实际战场环境，以垂直烟幕空间尺度计算模型、单点施放垂直烟幕计算模型为基础构建的多点施放垂直烟幕计算模型。根据如下模型解算配置诸元，等间隔多点顺风配置发烟装备，可实现垂直烟幕的对空遮蔽。

步骤1取x′=x′A=s0=(u×(t-tr))2，得到：

(19)

判断：若Qp>Qmax，需取s0=s0+Δ(Δ为计算步长，可根据解算精度需求设定为2，1.5，1，…，0.1等任意值)循环解算直至满足条件；然后，计算单点同时发烟的装备数量n=QpQ0. 其中：Q0为单个发烟装备最大源强，对于发烟车Q0≥Qe，发烟罐Q0=Qt；Qmax为单点最大源强，需根据实际进行界定，例如发烟车一般单点单车布设，可取Qmax=Q0.

步骤3基于lsk0及成烟时间获得发烟点间隔a=min(lsk0,(u×(t-tr))2)。

步骤4基于所需要的有效烟幕墙长度lsk，确定发烟点个数N=lska。

至此，完成了地面发烟装备阵地配置诸元的解算。

5 模型分析评估

本文多点施放垂直烟幕本质上是单点施放垂直烟幕的空间几何叠加；故验证单点施放垂直烟幕计算模型即可实现对多点施放垂直烟幕计算模型的验证。由于遮蔽方程(9)式是所构建的单点模型的核心，其解算的正确性决定了模型解算结果的正确性。因此，本节将基于该方程和某型发烟装备(雾油烟幕)的历史定型试验数据对所构建模型进行分析验证。

5.1 试验方法

试验条件：气温T为常温；1 m高处风速u1为35 m/s(风向基本稳定)；大气垂直稳定度为逆温或等温，即n分别为离地2 m和0.5 m的气温；相对湿度Rh>40；试验场地开阔平坦，无明显沟坎，无高大树木，植被不高于50 cm.

主要器材：某型车载式发烟机1台，DRV-TCR310E型摄像机、CCD-TR75E型摄像机、M3000型摄像机等7台，录放像机3台，LYR-205型激光测距仪1台，TG332A型微量分析天平1台，塔层气象要素测试仪1套，对讲机10台。由于采用历史数据，试验器材的厂家信息等已遗失。

测试方法：1)零前测试程序：测试气象，确定预定风向及试验预定零时；按预定风向布设器材、仪器，并调试、启动、预热。2)零时测试程序：发烟机正式发烟，以此为实际试验零时；采用“无标尺”摄像及图像分析法[13]的标准步骤测试、采集，并处理数据。

5.2 试验分析

气象参数测试结果如表1所示；连续发烟试验处理后的测试结果如表2、表3所示。

表1 气象参数测试结果(平均值)

表2 烟幕施放参数

发烟机发烟高度设为2 m，忽略烟气热抬升影响，并忽略烟幕有效利用率问题，即假设Ku=1，雾油烟幕在中等湿度条件下的遮蔽质量为0.88，n=0.94对应大气稳定度为C(弱对流)，将参数代入(9)式并求解，可得到表3的计算烟高。通过表3中的数据对比可以看出，试验结果与计算结果的一致性较好，尤其在烟幕长度≤250 m范围内。其中：一方面，本文模型计算忽略了烟幕有效利用率问题，若加入该因素进行重新解算，则重新解算的烟高应小于现解算值；另一方面，试验数据来自于全景观测，采集数据时烟幕可能尚未稳定，故实测烟高可能小于实际稳定烟高。综合上述分析可知，模型解算值应小于实际烟幕扩散，模型未高估烟高；同时，如第1节中所述，雾油烟幕可理想地看作是红外遮蔽烟幕中的一员。因此，佐证了本文所构建模型应用于战场红外遮蔽烟幕使用的实时解算是合理可行的。

6 结论

本文从烟幕扩散模式选择到烟幕遮蔽方程建立，再到模型构建过程的严密推导可以看出，所给出的防御红外末制导武器的地面发烟装备阵地部署模型是较为科学的。结合雾油试验结果分析可以看出，所构建模型应用于实际战场红外遮蔽烟幕的解算是合理可行的。当然，该模型属于特定方位防御阵地部署模型，在使用中存在局限性：一方面，机载导弹存在极限距离，但对于巡航导弹可能不存在，此时烟幕墙无法实现对空防御；另一方面，地面施放烟幕在烟幕高度上劣于空中爆炸成烟，单独使用时烟幕要求高度不能过高。因此，实际使用中需要根据敌情、我情及环境条件选择保障方式，或者与多波段光电伪装武器系统射击辅助决策模型相结合，从而构成空地一体烟幕施放辅助决策模型，克服本文模型在烟幕高度上的使用局限性，增强对红外制导武器的防御能力。

表3 雾油烟幕遮蔽性能观测及计算结果

注：有效摄像时段内的实际烟长标准偏差为193 m，实际烟高标准偏差为10 m.