球冠形封头卧式储罐容积积分公式推导

邢子龙 邢云婷 董伟 白景红 李爽 石万辉

（中国石油吉林油田公司新立采油厂）

0 引言

球冠形封头卧式储罐是炼化装置的常用设备。某炼化装置的球冠形封头卧式储罐容积计算大多是用网上下载的软件推算而来，不同的软件计算的结果存在着一定的误差，另外有些软件受使用权限限制，现场随机输入不同液位高度求得储罐容积不尽方便。针对这些问题，采用数学积分方法，推导出球冠形封头卧式储罐容积计算公式，并将公式与Excel表结合，得出球冠形封头卧式储罐容积换算表，方便现场人员录入液面高度即可及时掌握各液面下的介质体积，解决了生产计量实际问题。

1 球冠形封头卧式储罐容积计算方法

1.1 计算思路

球冠形封头卧式储罐的容积由两部分组成，一部分是圆柱筒体容积，另一部分是两个封头容积。不同液位高度下球冠形封头储罐的容积可采用积分方法，通过计算求出圆柱面截球体的容积减去球内圆柱筒体部分的容积，再加上储罐筒体的容积就可以得到储罐的容积。

1.2 储罐筒体的容积计算

球冠形封头卧式储罐示意图见图1，剖面图见图2。图1中绿色部分为h液位下介质的体积。L0为圆柱筒体长度。

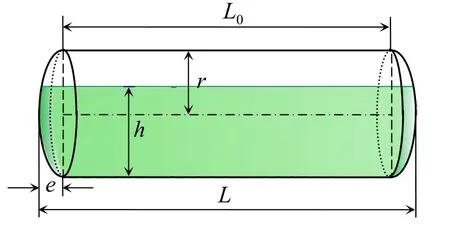
图1 球冠形封头卧式储罐示意图

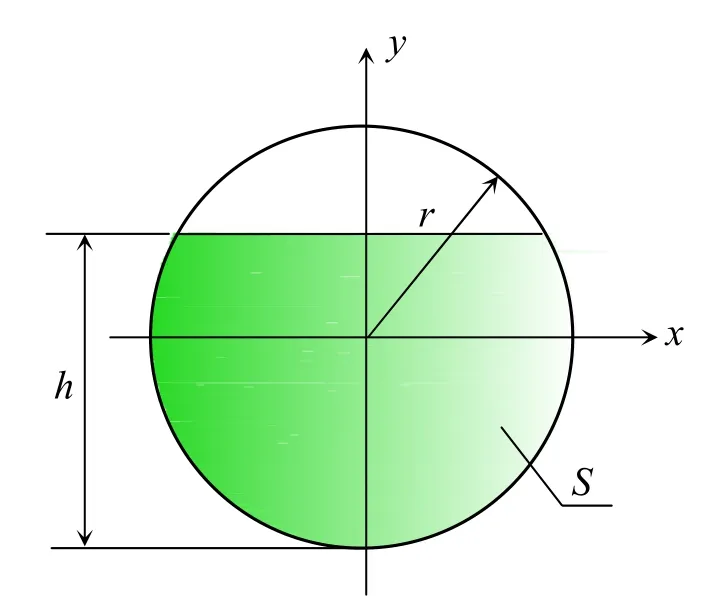
图2 储罐剖面图

S为液面高度h下的截面积：

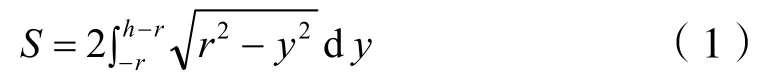
圆柱筒体内介质的体积v筒体为：

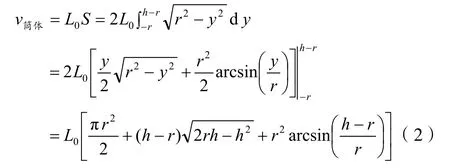
1.3 球冠形封头的容积计算

图3为圆柱面截球体示意图，绿色部分为球内圆柱筒体部分的容积，黄色和绿色加在一起为圆柱面截球的容积。图4为圆柱面截球体xz面的剖面图。

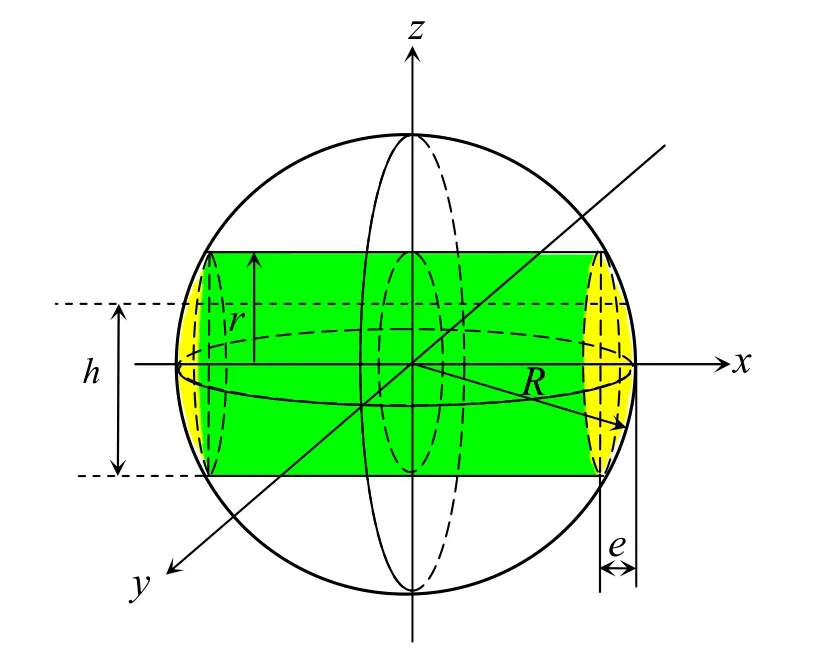
图3 圆柱面截球体示意图

假设半径为r的圆柱筒体中心线水平穿过半径为R的球的中心。根据给定罐体的半径r和球缺的厚度e，可以求出球形封头即球冠的半径R。球冠形封头半径得出：

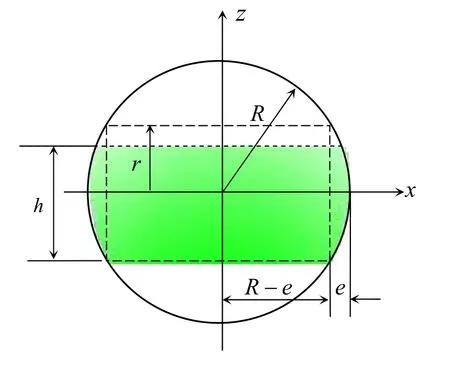
图4 圆柱面截球体剖面图

分别求出封头容积、球内圆柱筒体部分的容积和圆柱面截球的总容积。2个封头总容积：

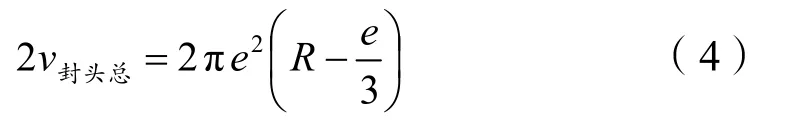
球内圆柱筒体部分的容积：

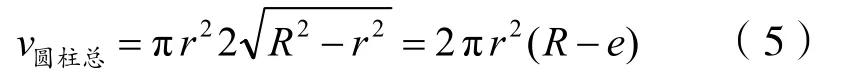
圆柱面截球体的总容积：

圆柱面截球体的容积积分公式为：

式（7）的积分非常复杂，式子中有虚数，被开方数中有负数，分母中有0。因R和r都是已知数，赋值相对简单，用matlab、adv calculus等软件积分求解，得到一个含有arctan和arcsin的关于x的方程。例如半径r=2的圆柱中心线水平经过半径R=4的球且穿过球体，那么代入（7）式后积分可得如下方程：

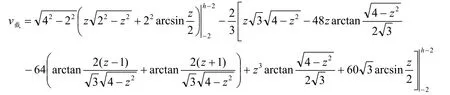
代入上、下限后得：

式（8）中前六项是代入上限的结果，把前六项依次输入Excel表并求和，得出前六项积分结果，见表1。可以看出：这六项的和在h＜r时，从负到正，从小到大；h＞r时由大变小；液位h=r=2时，六项和为 0。液位间隔相等，数值变化符合罐容中间大两端小的规律。

公式（8）的第七项是代入下限的结果，出现了分母为0的情况。经过输入大量不同的球和圆柱的半径值进行验算，结果证明：圆柱面截球体容积积分式（8）的最后一部分积分是个定值。因为h=r时的容积正好是圆柱面截球体总容积的一半，即根据式（6）求出=46.978 916 27输入Excel表进行计算，代入式（8）下限，得出圆柱面截球体容积的积分换算表，见表2。当h=2r时出现分母为0的情况，表中出现#DIV/0!，将填入即可。

表2 圆柱面截球体容积积分换算表

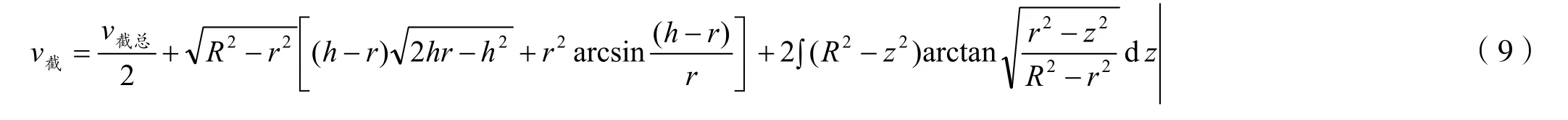
其中z=h-r。

把式（3）、式（6）代入式（9），得出圆柱面截球体的积分公式为：

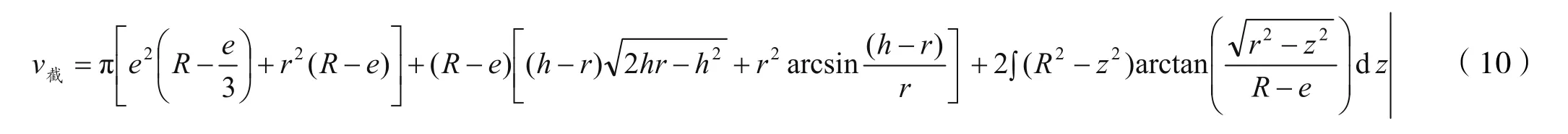
其中z=h-r。

1.4 封头的容积计算

利用式（10）和式（2）得出式（11）：

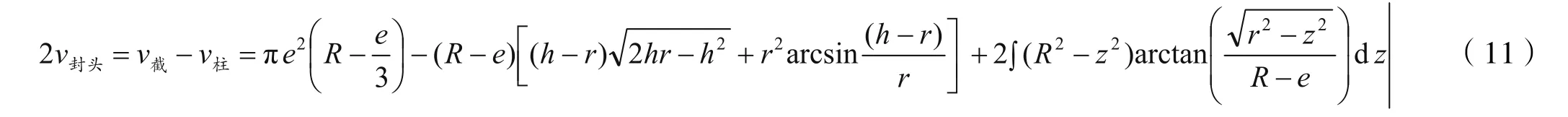
其中z=h-r。

1.5 储罐的容积计算

利用式（11）和式（2）可得出储罐的容积公式：

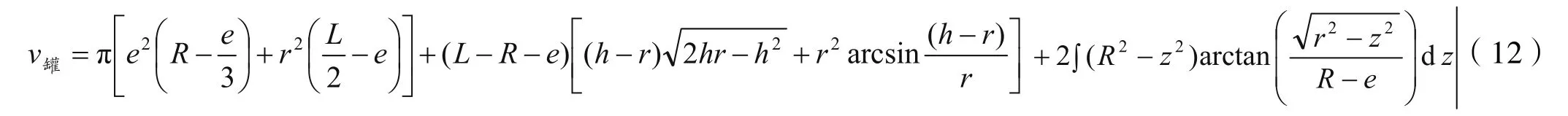
其中z=h-r。

2 应用实例

型号为SDH1600×8（6.7）-Q245的三相分离器为球冠形封头卧式储罐。罐长L=6.266 m（包括封头的两个直边0.025 m），圆柱筒体半径r=0.8 m，罐封头的厚度e为0.40 m。求出R=1.00 m。代入式（12）得储罐液位容积：

建立 Excel计算表，得出任意高度的储罐液位容积积分换算表，见表3。

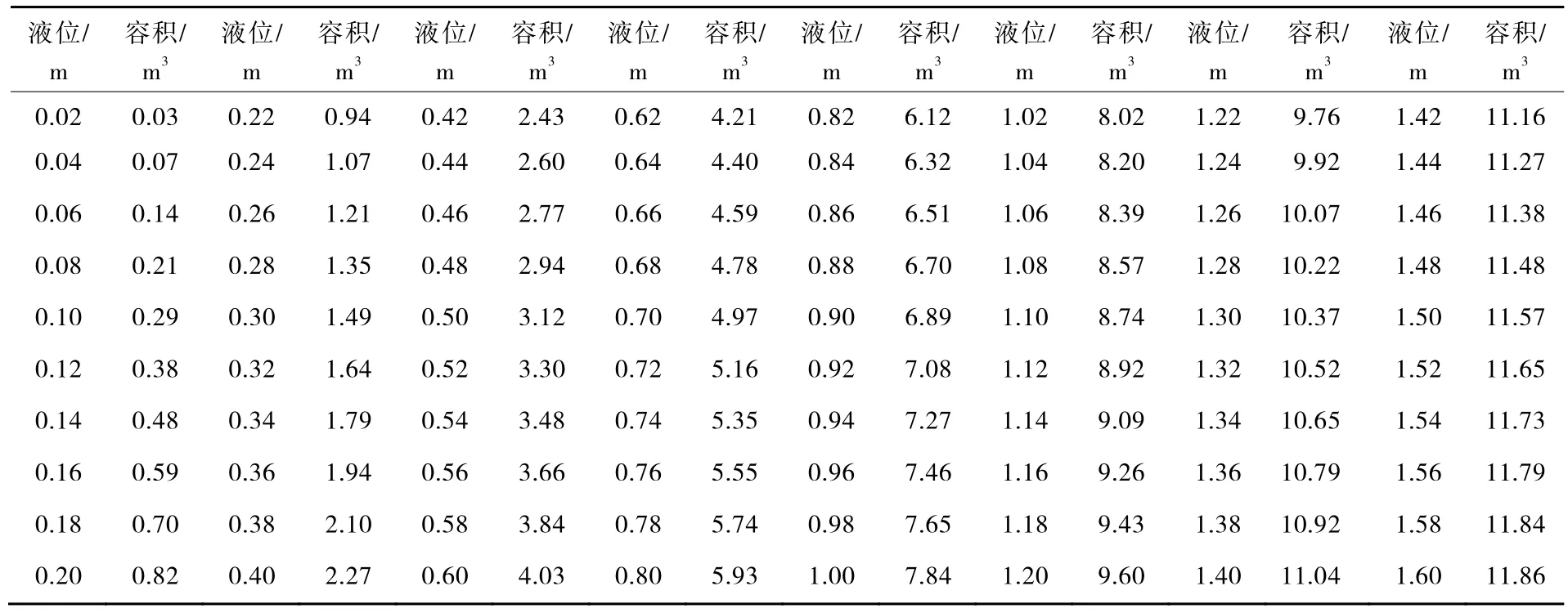
表3 储罐液位容积积分换算表

3 结论

从实际应用出发，为满足炼化装置常用的球冠形封头卧式储罐容积计量的需求，采用数学积分原理，推导出球冠形封头卧式储罐容积计算公式，并将公式各项输入 Excel表，即可方便快捷地得出球冠形封头卧式储罐容积换算表。在 Excel表输入不同液位高度，即可准确得到储罐容积。

在实际应用中，装车时介质体积采用以上公式计算出的储罐容积与卸车时流量计量的体积误差从0.5%缩小到0.1%，计量准确度大大提高。表明推导出的球冠形封头卧式储罐容积计算公式，计量结果准确可靠，较好地解决了生产计量实际问题。