基于可靠度理论的混凝土重力坝失事概率计算★
郑昊尧 金先龙 林绍清 杨士龚
(1.长江勘测规划设计研究有限责任公司,湖北 武汉 430010;2.贵州水投水务集团有限公司,贵州 贵阳 550000; 3.河南省新县水利局,河南 新县 465550)
本文基于可靠度理论对混凝土重力坝失稳失效概率进行计算,完成混凝土重力坝的风险评估。
1 基于可靠度理论的混凝土重力坝失事概率计算
1.1 大坝失稳失效概率计算
根据混凝土重力坝失稳失效的定义,大坝失稳失效[1,2]的功能函数为:
Z1=g(Mr-Ms)=Mr-Ms
(1)
其中,Mr为阻滑力矩;Ms为滑动力矩。
当Z1>0时,工程处于可靠状态,大坝未发生失稳失效;
当Z1=0时,工程处于极限状态,式(1)即大坝失稳失效的极限状态方程;
当Z1<0时,工程处于失效状态,大坝发生失稳失效。
在一定洪水重现期以及大坝设计规模下,大坝发生失稳失效的可靠度风险模型[3,4]为:
(2)
其中,Pf1为失稳失效概率;f(Ms)为滑动力矩的概率密度函数。
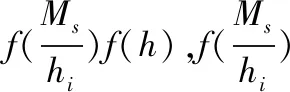
故式(2)可表示为:

(3)
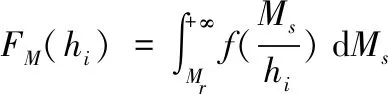
式(3)为大坝失稳失效概率计算模型,可以理解为失稳破坏一旦发生,就会立即导致大坝失效,即大坝失稳失效风险对大坝失效风险的贡献权重为l,这也是一种偏安全的分析方法。
1)阻滑力矩Mr的计算:
(4)
其中,Wi为作用于坝体上全部荷载(不包括扬压力)对滑动平面的法向分值,kN;U为作用于滑动平面上的扬压力,kN;Ri为Wi对滑动平面的作用力臂,m。
2)滑动力矩Ms的计算:
(5)
其中,Pj为作用于坝体上全部荷载对滑动平面的切向分值,kN;U为作用于滑动平面上的扬压力,kN;Rj为Pj对滑动平面的作用力臂,m;RU为扬压力对滑动平面的作用力臂,m。
3)失稳失效概率的计算。
结合上述各式,大坝失稳失效的功能函数改写为:
Z1=Mr(Wi,Ri)-Ms(Pj,Rj,U,RU)
(6)
大坝失稳极限状态方程为:
Z1=Mr(Wi,Ri)-Ms(Pj,Rj,U,RU)=0
(7)
1.2 可靠指标计算方法
1)JC法。
JC法,即当量正态化法,由拉克维茨和菲斯莱等人提出[5],被国际安全度联合委员会推荐使用。它适用于随机变量为任意分布下结构可靠指标的求解。本法通俗易懂,计算精度也能满足工程实际需要[6],见图1。
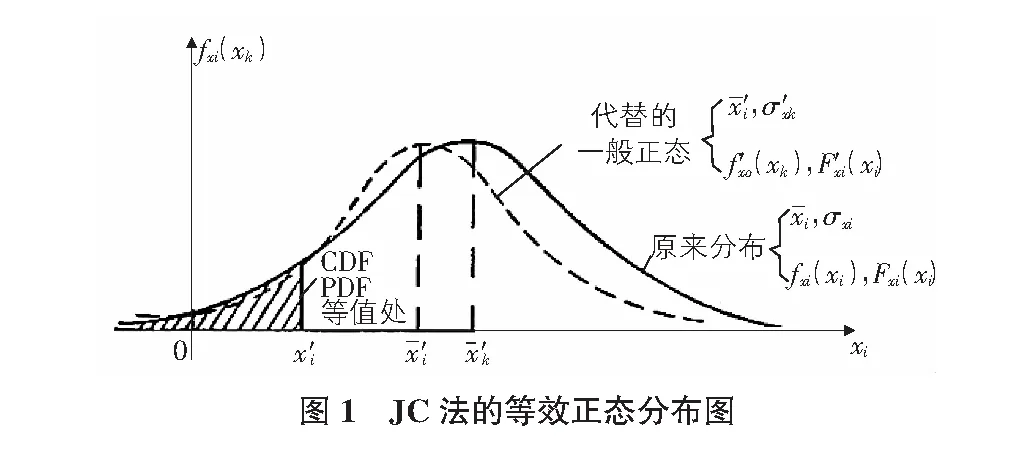
根据式(7)的极限状态方程和随机变量的统计量,利用JC法求解可靠指标β,具体步骤如下:
a.定一个β值。
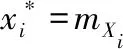
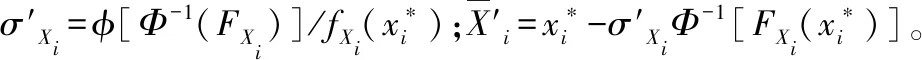

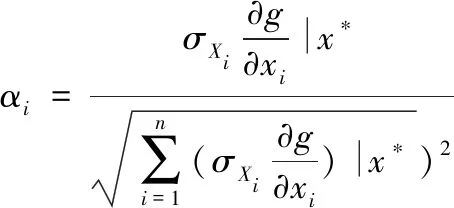
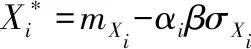
h.重复步骤c.~g.,一直算到前后两次所得的β的差值绝对值很小为止,进而得到失效概率。
2)蒙特卡罗法。
蒙特卡罗法求解结构失效概率的过程如下:
a.首先用随机抽样分别获得各变量的分位值,如图2所示。
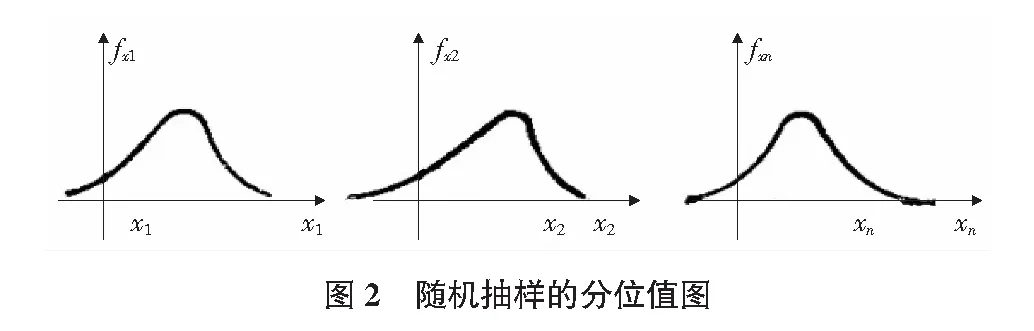
b.计算功能函数Z;设抽样数为N,每组抽样变量分位值对应的功能函数值为Z1,次数为L,则在大批抽样之后,结构失效概率可由下式算出:
Pf=L/N。
采用蒙特卡罗法计算出的失效概率为结构失效出现次数占总样本数的频率。
2 基于可靠度理论的陆水水库主坝风险
2.1 工程概况
陆水水库[7,8]位于长江中游南岸一级支流——陆水干流山谷出口处,枢纽控制流域面积3 400 km2,总库容7.06亿m3,是一座兼有防洪、灌溉、发电、航运、养殖等综合效益和水利试验任务的综合水利枢纽。工程等别为Ⅱ等,永久性主要建筑物级别为2级。防洪标准原为100年一遇洪水设计,1000年一遇洪水校核,可能最大洪水保坝。
2.2 失事概率计算方法
据陆水水库实际情况,结合洪水事件和失效模式,构造事件树,利用事件树分析计算陆水水库主坝失事概率,计算方法见表1。
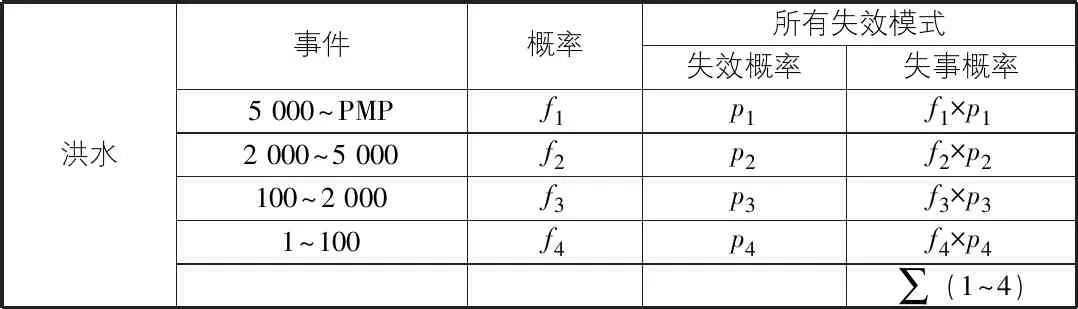
表1 陆水水库主坝失事概率计算方法
各洪水事件发生概率等于洪水重现期区间内洪水频率之差,计算结果见表2。
根据洪水事件构造事件树,事件树中分支事件如失稳破坏失效概率和强度失效概率采用可靠度法计算。

表2 各洪水事件发生概率计算
2.3 失事概率计算
利用一次二阶矩法对陆水水库主坝进行结构可靠度分析,主坝横断面图见图3。设随机变量为混凝土的抗拉和抗压强度ft和fc、上游和下游水位H1和H2、混凝土容重γ、坝顶附加荷载Q。计算时作用于坝体上全部荷载(不包括扬压力)对滑动平面的法向分值用W表示,作用于坝体上全部荷载对滑动平面的切向分值用P表示,扬压力用U表示,上下游水压力用P1,P2表示。计算合力和力矩(应力以压为正)见表3。
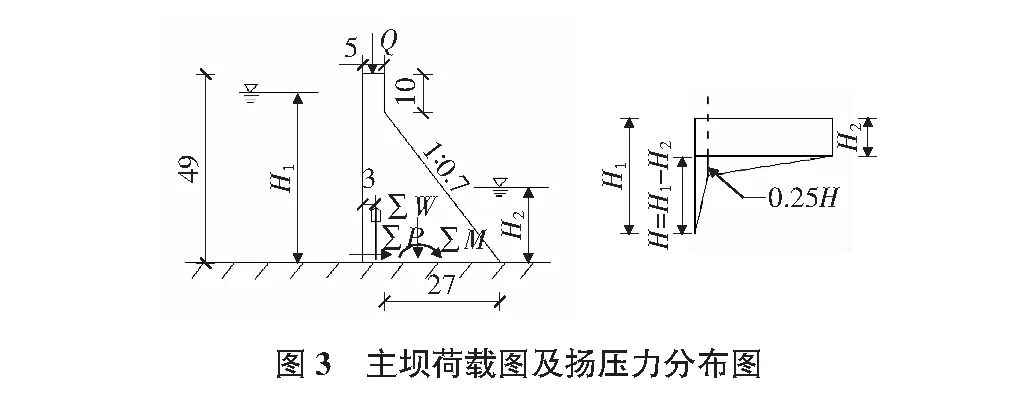
表3 合力和力矩计算表
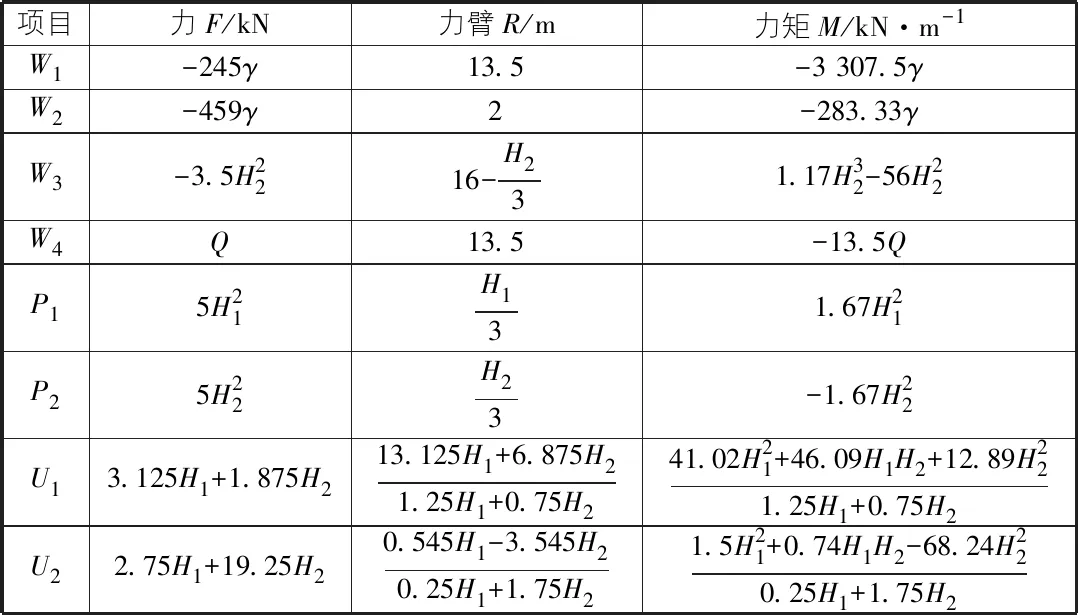
项目力F/kN力臂R/m力矩M/kN·m-1W1-245γ13.5-3 307.5γW2-459γ2-283.33γW3-3.5H2216-H231.17H32-56H22W4Q13.5-13.5QP15H21H131.67H21P25H22H23-1.67H22U13.125H1+1.875H213.125H1+6.875H21.25H1+0.75H241.02H21+46.09H1H2+12.89H221.25H1+0.75H2U22.75H1+19.25H20.545H1-3.545H20.25H1+1.75H21.5H21+0.74H1H2-68.24H220.25H1+1.75H2
由表3可以算出:
已知T=32 m,计算得到:
上游坝踵应力:
下游坝址应力:
考虑大坝失稳失效概率和强度失效概率,得到大坝失稳失效功能函数:
对应不同洪水事件的随机变量的统计值分别见表4。用JC法得到各方程的可靠指标β和失效概率Pf,计算结果见表5。

表4 出现概率为0.02%的洪水位下随机变量统计表

表5 主坝失稳破坏失效概率计算结果
3 结语
基于可靠度理论对混凝土重力坝失稳失效概率进行计算,完成混凝土重力坝的风险评估。该方法可为混凝土重力坝风险评估提供一定的技术支撑。

