基于结构方程模型的计算思维能力影响因素分析
蔡荣华 樊蒙蒙


摘 要 旨在探讨学生的计算思维能力和各种变量之间的关系是否存在,并测试这些变量是否能预测他们的计算思维能力水平,然后产生一个来解释和预测计算思维能力与各种变量之间关系的模型,也就是关系筛选模型。根据研究结果发现,计算思维能力是可以由一些变量预测的。
关键词 计算思维;结构方程模型;计算机科学
中图分类号:G652 文献标识码:B
文章编号:1671-489X(2019)02-0063-05
1 前言
计算思维并不是一个新概念,而是自20世纪60年代以来在计算机科学领域中强调的一项重要能力。对年轻人来说,计算思维的发展已经变得至关重要,这是为了培养未来的一代人,他们需要与技术结合,获得创造力和解决问题的能力。在此背景下,美国国际教育技术协会(ISTE)强调,年轻人应该准备成为计算型的思考者,他们能够理解如何利用当今技术解决未来的问题。本研究的重点在于K-5~K-12教育水平上各种因素对计算思维(CT)能力水平的影响。
2 计算思维
计算思维定义 周以真将计算思维表达为一种思维活动,就是运用计算机科学的思想方式及基础概念进行问题解答和系统设计,像计算机科学家一样思考问题、理解问题、解决问题。ISTE和CSTA(美国计算机科学教师协会)将计算思维能力定义为算法思维、创造性思维、逻辑思维和问题解决能力的反映。美国国家研究理事会(NRC)将数学和计算思维作为K-12科学教育的主要实践。后来,ISTE将计算思维定义为创造力,算法思维,协作性、批判性思维,问题解决等的共同体现。考虑到这些定义,计算思维能力与众多变量之间的关系是具有可传达性的。
计算思维能力影响因素 本研究通过性别、教育水平、IT使用经验、每日使用互联网时间、数学课的成功及对数学课的态度、科学课的成功及对科学课的态度、信息技术课的成功及对信息技术课的态度、思维方式等11个变量来解释学生的计算思维能力水平。学生的计算思维能力与各种变量之间关系存在质疑,并测试了这些变量是否能预测计算思维能力水平。此外,产生一个模型来解释和预测计算思维能力和各种变量之间的关系。有关这些影响因素的研究假设如下。
H1:学生的性别对他们的计算思维能力水平有积极影响。
H2:学生的教育水平对他们的计算思维能力水平有积极的影响。
H3:学生IT使用經验对他们的计算思维能力水平有积极影响。
H4:学生每日使用互联网时间对他们的计算思维能力水平有积极影响。
H5:学生在数学课上的成功对他们的计算思维能力水平有积极影响。
H6:学生对数学课的态度对他们的计算思维能力水平有积极影响。
H7:学生在科学课上的成功对他们的计算思维能力水平有积极影响。
H8:学生对科学课的态度对他们的计算思维能力水平有积极影响。
H9:学生在信息技术课上的成功对他们的计算思维能力水平有积极影响。
H10:学生对信息技术课的态度对他们的计算思维能力水平有积极影响。
H11:学生的思维方式对他们的计算思维能力水平有积极影响。
3 研究方法
研究模型 这项研究的研究小组由152名在2015—2016学年中的中学生(7、8和9年级)和高中生(10、11和12年级)组成。其中45.4%的参与者是女生,54.6%是男生。就教育水平而言,其中21.7%是中学生,78.3%是高中生。研究模型是根据文献而创建的。在这个模型中,研究假设用变量之间的单向箭头表示。图1显示了研究的假设模式。
数据收集 研究中使用了三种不同的数据收集工具,第一个是“个人信息表”,第二个是“计算思维能力量表”,第三个是“思维方式量表”。个人信息表采用李克特样式,由18个项目组成,收集的数据涉及参与者的个人信息,获取信息技术和使用这些技术的情况、数学、科学和信息技术方面的学术成就以及对这些课程的态度。
计算思维量表是由Korkmaz等人开发的,由29个项目和五个因素组成。在五个因素中,“创造力”子维度由八个项目组成,“算法思维”子维度由六个项目组成,“协作”子维度由四个项目组成,“批判性思维”子维度由五个项目组成,“问题解决”子维度由六个项目组成。本研究中计算的克朗巴哈系数处于较高水平(0.916)。
思维风格量表是由Fer改编(见表1)的李克特样式的量表。本研究采用13个项目,在立法型、执行型和司法型等方面进行研究,并将其纳入思维范围的功能维度。为了适应相关的教育水平,Y?ld?z进行了调整,并且进行了有效性和可靠性研究。在这项研究中计算的克朗巴哈系数是0.899。
数据分析 本研究采用网上创建的问卷调查,将数据收集工具应用于研究小组。在研究中使用结构方程模型(SEM)来质疑学生的计算思维能力和各种变量之间的关系的存在,并测试这些变量是否能预测他们的计算思维能力水平,然后产生一个模型来解释和预测计算思维能力和各种变量之间的关系。
本研究中通过LISREL 8.51程序预测了观察到的变量,并创建了模型。为了揭示推荐模型中关系模式的相容性水平,使用和审查了χ2(卡方拟合指数检验)、RMSEA(近似均方根残差)、GFI(拟合优度指数)、CFI(比较拟合指数)、NFI(规范拟合指数)指数测试。
4 研究结果
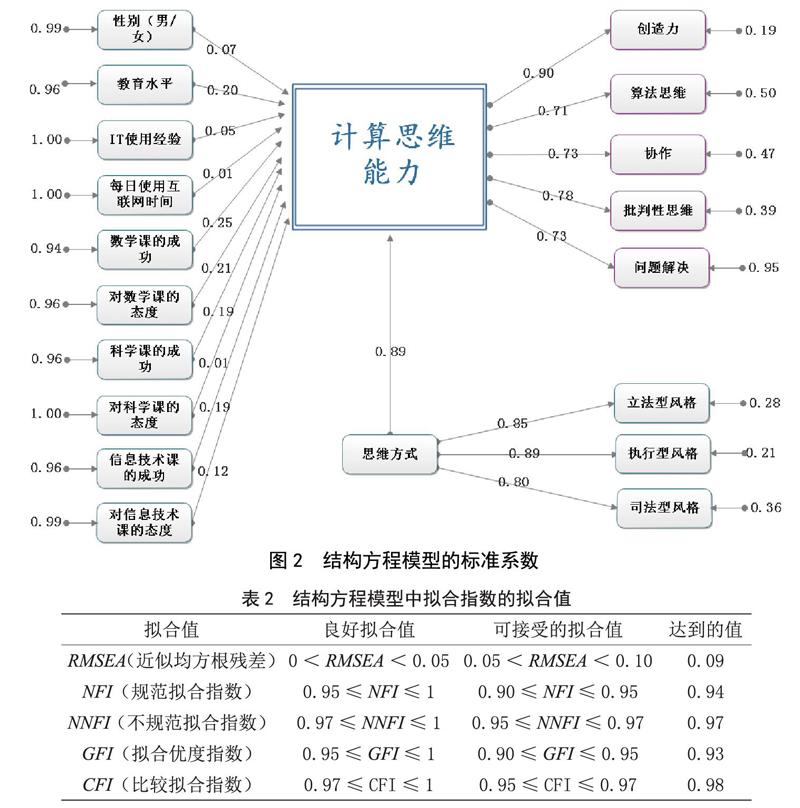
图2显示了结构方程模型的系数,该模型由根据应用于学生的数据收集工具获得的数据选择的变量组成。在确定与结构方程模型的相关性之前,有必要测试具有潜在变量的测量模型的拟合指数。此外,还可以在结构方程模型中用单个模型分析所有模型。表2列出拟合标准的拟合范围和研究中获得的值。
χ2=495.23,自由度df=134,假定值p=0.000。RMSEA的值是0.10,所获得的值表示可接受的匹配。同样,NFI为0.94,NNFI为0,97,GFI为0.93,表明该模型呈现出可接受的结果。此外,发现该模型的各项指标均显著高于0.05水平(χ2、RMSEA、NNFI、NFI、CFI和GFI)。根据拟合指数的计算值,确定已形成的结构方程模型的能力水平处于良好和可接受的水平。数据和结构方程模型之间存在一种可接受的和谐关系,旨在确定计算思维与影响CT因素之间关系的水平与方向。据了解,为确定结构方程模型的充分程度而进行的合规性指数与计算值相吻合。
根据图2对结构方程模型进行分析,“计算思维能力”被确定为潜变量。模型拟合指标具有显著性(χ2=495.23;p=0.000)。
当分析学生计算能力的变量时,发现“思维方式”是最显著的变量,具有最高的相关系数(g=0.89);然后是变量“数学课的成功”(g=0.25);再次是变量“对数学课的态度”。计算思维能力潜变量有五个子维度,其中子维度“创造力”具有最高的因子负荷。思维变量的思维方式由三个子维度构成,其中子维度立法型具有最高的因子负荷。
根据关系系数,预测变量在计算思维能力水平上的相对显著性顺序为思维方式、数学课的成功、对数学课的态度、教育水平、科學课的成功、信息技术课的成功、对信息技术课的态度、性别、IT使用体验、日常互联网使用时间和对科学课的态度。
根据表3,对数学课的态度变量方差值(var=1.29)最高,发现教育水平变量方差值(var=0.17)是最低的。此外,考虑变量之间的协方差值,发现最高值(cov=0.38)是在对数学课的态度和数学课的成功之间,最低值(cov=-0.12)是在日常互联网使用时间和数学课的成功之间。
根据表4,H2假设被接受(β=-0.325,p<0.05,t=
-3.514)。因此,可以说K12中教育水平的提高与一般的计算思维水平相平行,可以认为认知发展是CT能力发展的重要因素。
H5假设被接受(β=0,142,p<0.05,t=1.627)。因此,可以预期数学好的人比数学差的人具有更高的计算思维能力。这种情况可以解释为计算思维结构需要数学思维。Wing通过将计算思维描述为涉及数学、工程和科学思想的概念来支持这一发现。
H7假设被接受(β=0.158,p<0.05,t=1.936)。因此,可以认为在科学课程中参与者的成绩与计算思维能力的水平存在正相关关系。在此背景下,NRC强调科学教育范围内最基本的应用之一就是计算思维,另一个是数学教育。因此,可以预期在科学教育范围内进行的培训具有支持学习者计算思维能力发展的结构。
H11假设被接受(β=0.704,p>0.05,t=12.150)。因此,与其他变量相比,思维方式对计算思维能力的影响达到最高水平。此外,思维方式量表包含三个子维度,并且已经确定每个子维度和计算思维之间存在正相关关系。
其余假设都被拒绝。
5 结语
研究发现,计算思维被思维方式、数学课的成功、对数学课的态度、教育水平、科学课的成功、信息技术课的成功、对信息技术课的态度、性别、IT使用体验、日常使用互联网时间和对科学课的态度等因素影响。根据这些发现,确定了在有效模型中预测计算思维的最有效变量是思维方式。调查结果与文献中的研究结果一致。由于本研究中认为思维方式是预测计算思维能力的重要因素,因此,人们认为学习者的认知和思维方式以及具备这种特定的意识,会使他们在获得计算能力方面更加成功。学习思维方式可以增强学生的创造性学习能力并提高他们的能力,如问题解决和抽象。教师应该支持和探索学习者的思维方式。
对于未来的研究,建议在学习环境设计研究的基础上,根据学习者的思维方式,通过考虑有效模型来探究计算思维能力,并研究这些课程的效果,从而对课程进行评估。
参考文献
[1]Wing J M. Computational Thinking[J].Communications of the ACM,2006(3):33-35.
[2]ISTE & CSTA(2011). Operational Definition of Computational Thinking for K-12 Education.[EB/OL].[201-707-01].http://www.iste.org/docs/ct-documents/computational-thinking-operational-definition-flyer.pdf?sfvrsn=2.
[3]刘向永,周以真,王荣良,等.计算思维改变信息技术课程[J].中国信息技术教育,2013(6):5-12.
[4]郁晓华,肖敏,王美玲.计算思维培养进行时:在K-12阶段的实践方法与评价[J].远程教育杂志,2018,36(2):18-28.
[5]张立国,王国华.计算思维:信息技术学科核心素养培养的核心议题[J].电化教育研究,2018,39(5):115-121.

