生物复杂网络motif发现的并行算法

杨伏长 朱嘉富 孙佳敏 谢江

摘 要：生物复杂网络motif发现是一种研究生物网络的重要方法，它基于复杂网络的理论研究，以新的视角来研究生命现象和生命机制，但是在处理较大的网络规模或者需挖掘较大的motif时计算效率低。针对这个问题，在现有串行网络motif发现算法ESU的基础上，提出一种基于消息传递接口（MPI）的并行化ESU算法。该方法在ESU計算过程中优化了节点值以解决节点值依赖问题，并以ESU算法的子图发现策略统计各节点子图数，利用动态规划策略寻找最佳节点分配策略以解决负载不均衡问题。模拟网络数据和真实生物网络数据的实验结果表明，并行化ESU算法优化了节点值依赖问题，实现了基于动态规划的负载均衡策略，其运行时间比串行算法缩短了90%，并且该并行算法对不同类型不同规模的网络都具有较强的适用性，有效地提高了网络motif发现问题的计算效率。

关键词：网络motif发现;子图枚举;同构比较;并行化;消息传递接口

中图分类号： TP301.6

文献标志码：A

Abstract： Biological complex network motifs discovery， based on theoretical research of complex networks， is an important method for studying biological networks， which provides a new perspective on life phenomena and life mechanisms. However， it computes inefficiently when dealing with large networks or mining big motifs. On the basis of existing serial ESU （Enumerate SUbgraph） algorithm of network motifs discovery， a parallelized ESU algorithm based on Message Passing Interface （MPI） was proposed. The node values in ESU algorithm were optimized to solve the problem of node value dependency， the number of subgraphs was counted by using subgraph discovery strategy of ESU algorithm， and a dynamic programming method was used to determine optimal node allocation strategy to satisfy load balancing. The experiments on simulated and biological networks show that the parallelized ESU algorithm addresses node value dependency and realizes a load balancing strategy， which saves more than 90% running time compared to serial algorithm. Furthermore， the parallel algorithm is suitable for different types and different scales of networks， and effectively improves computation efficiency of network motifs discovery.

Key words： network motifs discovery; Enumerate SUbgraph （ESU）; homogeneous comparison; parallelization; Message Passing Interface （MPI）

0 引言

生物网络比对对网络医学和物种演化等领域的发展有着重大的意义[1]，其中，一项很重要的研究就是生物网络motif发现。生物网络motif发现是指在生物网络中寻找所有特定大小、拓扑结构一致的子图[2]，它包括在生物网络中枚举子图和计算子图之间的同构关系等问题。生物网络motif是生物网络的基本单元，它所表现的局部性质与网络的构成机制密切相关，对它的研究可以加深对生物网络的结构和功能的理解，有助于揭示很多重要的生物学问题[3];然而精确识别网络motif是一个计算复杂度很高的问题[4]，每一个枚举的子图都需要执行同构比较，而子图之间同构关系的计算一直是NP（Non-deterministic Polynomial）难问题，无法通过改进算法来降低其时间复杂度。随着生物网络研究的规模和motif的大小不断增大，参与枚举和同构比较的子图数呈指数级别的增长，其计算量越来越大，给网络motif的发现带来了挑战。

当前网络motif发现研究算法仍以Wernicke[5]于2006年提出的ESU（Enumerate SUbgraph）算法为主流，其衍生算法如Ribeiro等[6]于2010提出的基于G-Tries的改进算法，通过G-Tries来存储motif所枚举的图，减少了比较子图同构次数来降低时间、提高性能;Khakabimamaghani等[7]于2013年提出了QuateXelero算法，该算法利用四分树结构来减少同构计算次数;Luo等[8]于2018年提出的LCNM（Large Co-regulatory Network Motifs）算法，通过结合枚举和随机化ESU算法，提高了网络motif发现的计算效率。

目前，已有的网络motif发现算法，在计算规模上都存在瓶颈[9]。随着生物网络数据获取的渠道越来越多，生物网络规模越来越大，对计算效率的要求也会越来越高，因此，实现高效的并行化网络motif发现算法是很有必要的。本文从串行的ESU算法着手，分析算法中各个部分的耗时，针对算法中耗时最长的部分，以消息传递接口（Message Passing Interface， MPI）為基础实现并行化，并结合优化节点值和动态分配节点策略改进并行算法，最后通过仿真数据和真实数据进行了分析和讨论。

1 网络motif发现

网络motif发现问题本质上是统计各种非同构子图在网络中出现的频率，并与随机网络所产生的子图的频率进行比较，出现频率明显高于随机网络的那些子图可能会揭示网络的重要功能[2]。然而，随着估计重要性方法的出现，网络motif发现问题的计算负担就落在原始网络的子图统计上[10]，因此网络motif发现过程就是各种子图的统计过程，其形式化定义[11]如下：

定义1 网络motif发现。给定一个网络G和参数k，找出所有大小为k的子图，并根据各个子图间的同构关系进行分类。

根据子图间的同构关系进行分类是网络motif发现过程中计算量最大的部分，目前尚无多项式级别的算法能够完成这个分类过程，即使在较高效的算法如nauty算法[12]，其在最坏情况下，计算复杂度仍达到O（n！）。

2.1 串行ESU算法

2.1.1 算法实现原理

ESU算法是一种枚举子图的motif发现算法，ESU算法可以大致分为网络构建、枚举子图、子图同构比较和统计子图结果四个步骤，其中ESU算法所提出的枚举子图的过程保证了所枚举子图的唯一性和子图数的准确性，枚举子图的过程是后续子图同构比较过程的实现前提，因此，下文对ESU算法的枚举子图过程展开介绍。

ESU算法的输入为边集的形式，节点的序号（在后文中使用节点值来表示节点的序号）以连续的数值表示，利用基于节点值的方式构建图，在不断构建的过程中记录节点值比节点本身大的邻居，以防止重复搜索子图，在搜索子图的过程中，不断加入节点值比自身大的邻居，并将新加入节点的符合规则的邻居也作为待搜索节点，以防止遗漏子图。ESU算法伪代码[5]描述如下：

其中，输入用节点集V和边集E描述的图G，和给定一个k用来描述motif的大小，算法将会输出所有在G中motif大小为k的子图。算法从V中的每一个节点v开始，初始时确定VExtension集合，VExtension集合包含了所有节点值大于v的邻居节点，伪代码中用N来描述邻居关系，VSubgraph集合初始化为{v}，是存储子图节点值的集合，然后调用ExtendSubgraph函数进行子图搜索和同构比较;ExtendSubgraph函数中，其关键步骤在于对VExtension中的每一个节点w进行如下操作：将w从VExtension集合中移出并加入VSubgraph集合，更新VExtension集合，新的VExtension集合由VSubgraph集合的所有节点值大于v的邻居组成，伪代码中用Nexcl来描述这种新的邻居关系，每当VSubgraph中的节点数达到了指定的k大小，就执行网络同构比较。

ESU算法枚举子图的过程如图1所描述，在图1中，枚举过程被描述为树形结构，这种树被称为ESU树[5]。ESU树是建立ESU算法正确性的基础，它能保证所枚举的每个子图不重复，其向下延伸的过程正好对应了EnumerateSubgraph函数。其中，图G是一个包含9个节点9条边的拓扑网络，其节点值依次从1到9。算法从Root开始，枚举图G所有存在的子图，图1中最后输出16个叶子节点，对应为所有motif大小为3的子图。

2.1.2 算法分析

ESU算法中最重要的两个步骤就是子图枚举和子图同构比较。

子图枚举是ESU算法的核心步骤，通过记录节点值比自身大的邻居，以防止在搜索过程中得到重复的子图，但是，基于节点值的枚举过程，会导致各个计算量集中在某些特殊的节点，比如一些邻居很多而且邻居节点值都比自身大的那些节点（如图1中1，2，3节点），这种问题被称为节点值依赖问题，这种问题在串行过程中体现不出来，但是在并行过程中，一旦出现这种问题，就会造成负载不均衡，大幅度影响并行的性能。

子图同构比较是整个串行ESU算法耗时时间最长也是计算复杂度最高的部分[7]，在串行ESU算法中，子图同构使用了高效的nauty算法[12]，基于子图枚举的结果，对每个子图进行同构比较;然而nauty算法仅仅是提高了两个子图之间同构比较的计算效率，它并不能解决并行过程中存在的其他问题，如负载不均衡问题，而这些问题正是提高并行效率的关键。

由于每一个枚举的子图都进行同构比较的计算，枚举子图的结果就直接决定了各个节点子图同构比较的计算量，所以本文对子图枚举的过程进行并行处理，以均衡各个节点的计算量。

2.2 ESU算法并行化

由于子图同构比较是整个算法最耗时的部分，因此并行处理的关键就是均衡各个节点所需比较子图同构的次数。本文就均衡子图同构比较次数上，提出了结合优化节点值和动态规划分配节点的改进方法。

1）优化节点值。由于节点值依赖问题使得在枚举子图的过程中，部分枚举的子图集中在少数的节点上，直接导致各个节点所需比较子图同构的次数差异很大，对并行性能造成很大影响，因此在2.2.1节中，优化了节点值，改善了节点值依赖问题。

2）动态规划分配节点。由于各个节点出发枚举的子图数不可能完全一致，在分配任务时就可能造成各节点计算量不一致，导致负载不均衡，因此在2.2.2节中，提出了基于动态规划的节点分配策略，实现了负载均衡。

2.2.1 解决节点值依赖问题

由于ESU算法是根据输入网络的节点值来记录相应符合条件的邻居以防止重复搜索，造成了网络各个节点之间的计算存在一定的依赖关系。对于网络的不同输入形式，比如同一拓扑结构的网络，其节点赋予不同的节点值，会导致同一节点在不同节点值的情况下计算量差异很大，最典型的便是那些度很高的节点，如果其邻居的节点值都大于它本身会使计算量全部集中在这些度很高的節点上，就会对并行的性能造成很大的影响，因此本文在网络分发之前进行节点值优化，步骤如下：首先统计各个节点值在边集中出现的频次，然后将节点值集合从大到小依次赋给出现频次从大到小的节点，完成对节点值的优化过程。具体如图2所示。

对于图2中两个同一拓扑结构的网络，网络A中那些度很大的节点的节点值都很小，网络B那些度很大的节点的节点值都很大，两种网络分别调用ESU算法进行计算，得出各个节点出发所需计算比较同构子图数如表1所示。

结合分析表1中的数据和图1的拓扑结构可知，当节点度的大小与节点值的大小成正比时，各个节点出发的计算量差异相对较小，也就是说节点值优化使得各个节点的计算量相对均衡。

2.2.2 网络节点分配过程

由前面的分析可知，对ESU算法进行并行化处理的关键在于将搜索入口节点分发给各个进程以实现并行计算，而对ESU算法的并行化过程存在两个很明显的特点：

1）每个搜索入口顶点进行深度搜索时所需要的图的区域是未知的，因此每个搜索入口都需要对整个图的区域进行搜索，无法对图进行区域分发;

2）每个搜索入口顶点进行深度搜索时所得到的子图数是未知的，那么在将所有的子图进行同构比较时，所需的时间也是未知，所有节点所花费的时间不一，对并行性能会造成很大的影响。

对于特点1）可知，需要将整个图分发给所有进程，每个进程都存储一个图的内存，虽然会占用一定的资源，但是一般的图占用的内存都很小，对于现代内存大都大于10GB以上的计算机而言，这点内存显得微不足道。

对于特点2）可知，每个搜索入口节点所需的计算时间差异很大，对于并行算法而言，以顶点作为分发手段不是明智的选择，需要考虑其他的负载平衡策略，当仔细分析算法计算过程时间消耗分布时，发现与ESU算法中深度搜索得到的子图数这个过程相比，将所得到的每个子图进行同构比较的时间要远远大于搜索的过程，于是，本文在原有的算法上增加了一步：先从每个搜索入口节点出发，深度搜索得到每个节点所需同构比较的子图数，接着不进行同构比较，而是依据各节点统计的子图数对所有节点进行排序，同时使用动态规划将顶点分配到各个进程，使得进程子图数总和之间的方差最小。具体步骤描述如下。

1）使用ESU算法的子图发现策略统计各节点子图数;

2）依据子图数将节点进行降序排序;

3）确定节点与进程号之间的关系：首先将所有子图数求和得到SubgraphSum，将其除以进程数n得到每个进程所需比较同构子图数的上限AverageSum，确定每个进程初始子图数CurSum为0，不断将已排序的节点移出并逐个赋给不同进程，并更新CurSum，对于每一个进程，如果CurSum>AverageSum，则不加入这个节点，并尝试将节点加入下一个进程。

2.2.3 ESU算法并行框架

3 实验与分析

3.1 实验环境

该程序运行在上海大学高性能计算集群自强4000平台，实验使用2台计算节点，每个计算节点使用2颗Intel E5-2690 CPU（2.9GHz/8-core），内存大小为64GB，集群节点间使用标准的Clos二层Infiniband网络架构。实验运行操作系统为CentOS 6.3，编程语言为C++，MPI库版本为IntelMPI。

3.2 实验数据

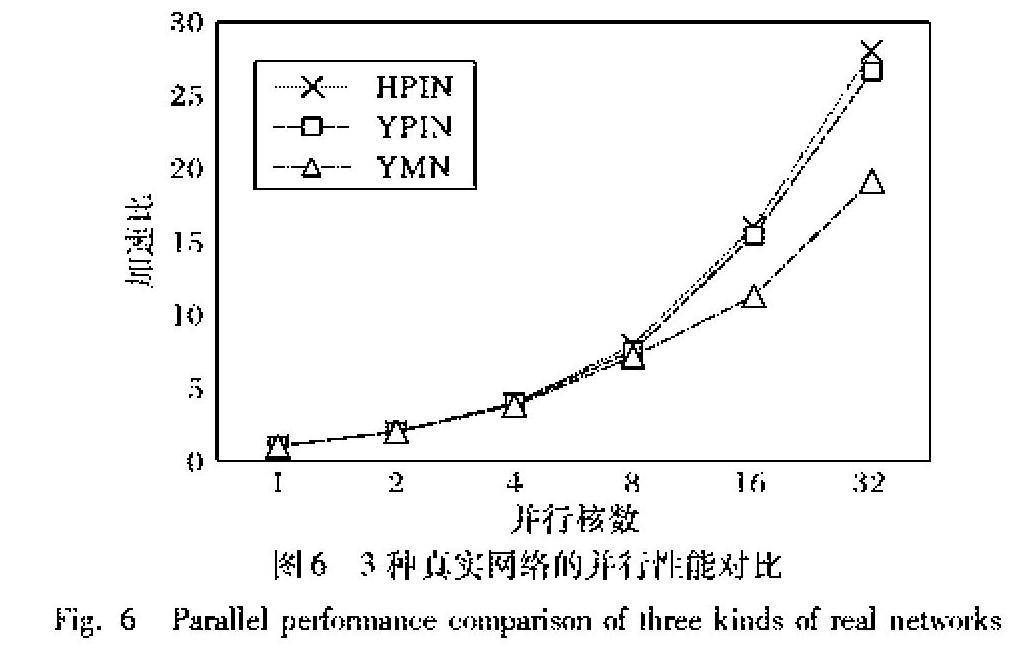
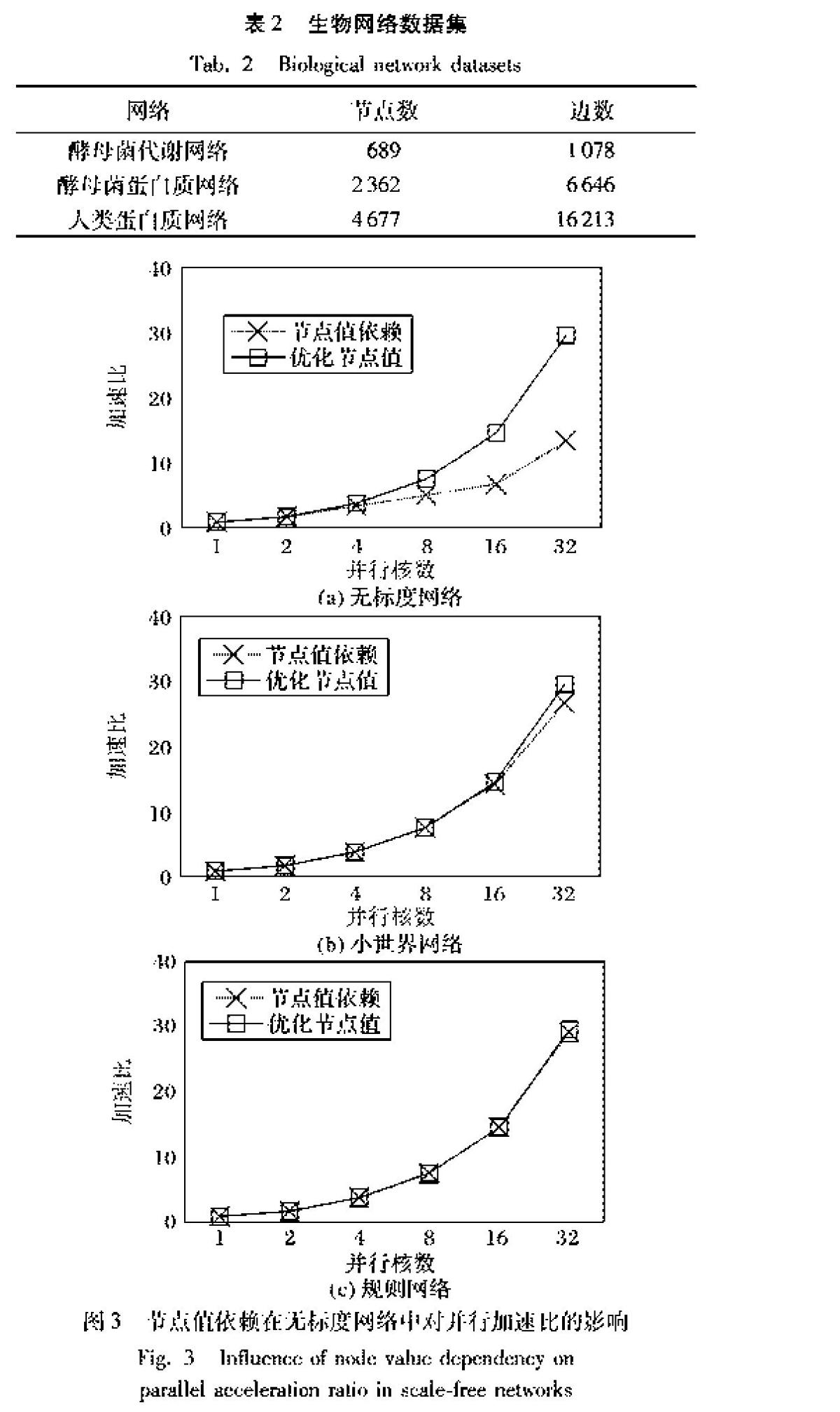
实验同时使用了模拟数据和真实生物网络数据进行性能分析，其中模拟数据使用NetworkX[13]的Python包模拟了三类不同的网络模型，分别是无标度网络模型[14]、小世界网络模型[15]和规则网络模型[16]，每类网络模型随机地改变边数和节点数，产生具有不同平均节点度的网络，以探讨在不同的平均节点度下并行ESU算法的性能。实验中使用固定的4000个节点，同时变化边的条数，分别为20000、40000和60000条边，来产生不同的节点平均度，分别是5、10和15，每种平均节点度模型均生成10个网络;真实生物网络则选取了酵母菌代谢网络、酵母菌蛋白质网络和人类蛋白质网络三个生物网络数据集，其节点数和边数如表2所示，其中：酵母菌的蛋白质网络和代谢网络数据集来源于Uri Alon实验室[2]，人类蛋白质网络数据来源于STRING（Search Tool for Recurring Instances of Neighbouring Genes）在线数据库[17]。

3.3 实验结果与分析

3.3.1 优化节点值依赖的结果

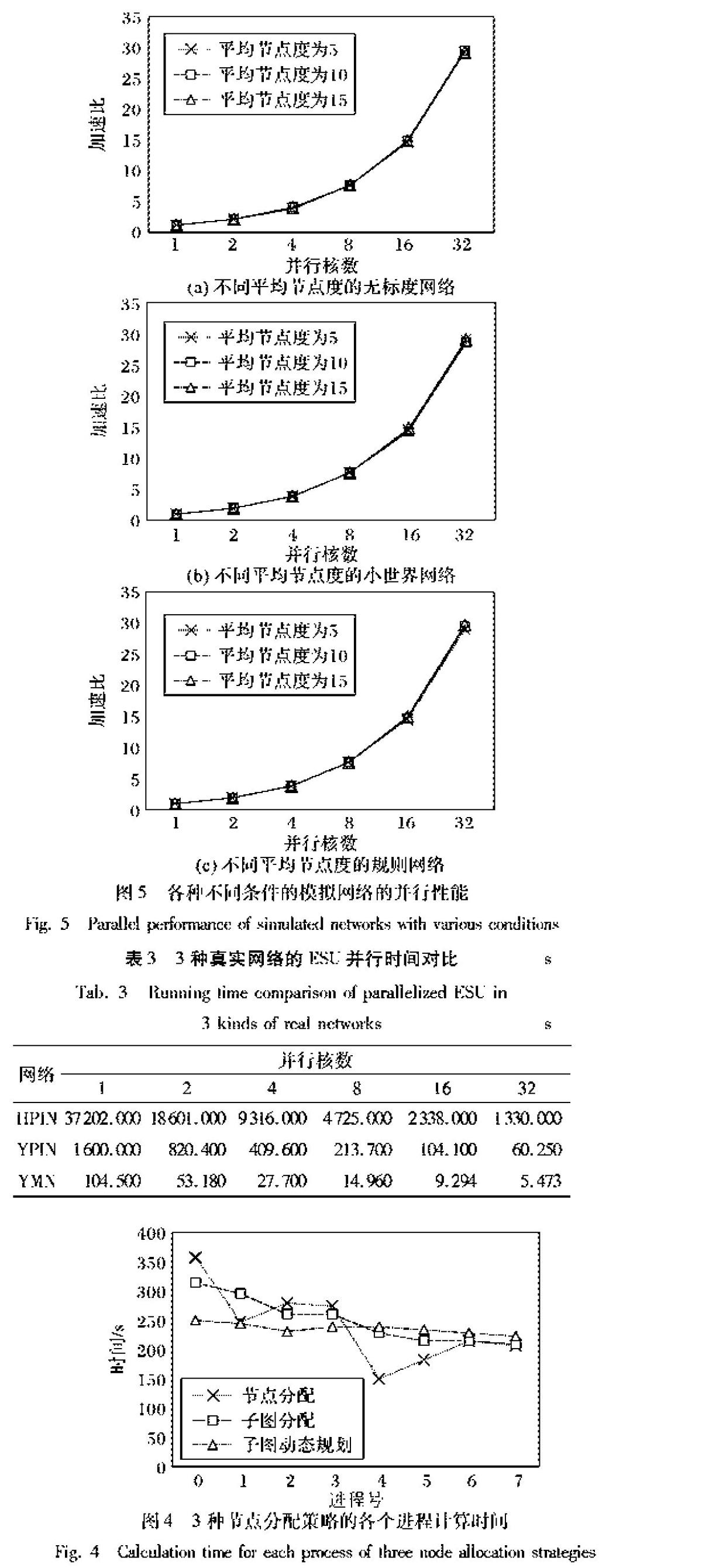
为验证有优化节点值策略和无优化节点值策略对网络并行性能的影响，本文对前文提到的3种模拟网络进行测试，每种模拟网络都在不同的motif大小以及不同的平均节点度下进行测试，各种条件下的测试结果都很相似，因此，本文选取其中一种测试条件下的测试结果进行描述，选取的条件为节点数为4000、边数为20000、motif大小为4，测试结果如图3所示。

从图3中可以看出，使用优化节点值策略与否对无标度网络模型的并行性能影响很大，而对小世界网络和规则网络的并行性能影响很小。这是由于小世界网络和规则网络的演化规则与节点演化的先后顺序无关。小世界网络中那些度很大的节点的节点值具有随机性，使用优化节点值策略对并行性能影响不大。规则网络中，各节点的度一致，其并行性能与使用优化节点值策略与否无关。无标度网络的演化模型恰好是一种节点值依赖问题的极端情况，最先演化的那些点恰好是度最大且节点值最小的点，而计算量正是集中在这些最先演化的点上，导致并行性能很差。使用优化节点值策略，对那些最度此句不通顺很大且节点值很小的点的节点值重新赋值，使各个节点所枚举子图的数量差异相对较小，从而提高并行性能。在进程数达到32时，未使用优化节点值策略的加速比为13.5，而使用优化节点值依赖策略的加速比为29.7。可见对节点值之间的依赖关系进行优化是非常有必要的。