基于CFD的大型立式轴流泵反向发电稳定性能分析
周 颖,郑 源,何中伟,汪昊蓝
(1. 河海大学水利水电学院,江苏 南京210098;2. 河海大学创新研究院,江苏 南京210098;3. 中国电建华东勘测设计研究院有限公司,浙江 杭州311100)
1 研究背景
泵站在我国南水北调工程中发挥着重要的作用,具有排涝防洪,解决农业用水问题等。部分水泵可进行反向发电获得一定的经济效益,但当水泵在进行反向发电时,水流流态受进出水流道的影响,压力脉动较水泵工况下会发生一定的改变,严重时甚至对厂房结构形成威胁。
对轴流泵压力脉动及反向运行方式的研究很多。张德胜[1]等通过模型试验研究了斜流泵叶轮进口段至导叶出口段设置7个压力脉动处,不同工况下高比转速斜流泵内部压力脉动特性和规律;黎义斌[2]等通过设置压力脉动监测点,研究动静干涉对混流泵内部流动非定常压力脉动特性的影响,并进行了试验与数值模拟的对比验证;罗旭[3]等采用CFX软件对离心泵的内部流场进行数值模拟,分析其不同监测点在不同流量下的压力脉动特性。施卫东[4]等针对轴流泵模型,对不同转速下的模型进行试验,分析压力脉动频率分布规律;张德胜[5]等对轴流泵在不同流量工况下的压力脉动特性进行了试验研究,分析压力脉动的位置及频率分布规律;杨建东[6]等对水泵水轮机在偏离设置工况下,进行了试验测量,分析各部分压力脉动形成的原因;王松林[7]等基于RNG k-ε湍流模型及输运方程空化模型,对小流量工况离心泵瞬态空化流动进行数值模拟,研究压力脉动在流道不同位置的分布规律;汤方平[8]等基于RANS方程和RNG k-ε模型,采用Ansys-CFX软件对轴流泵泵段进行了多工况三维非定常数值模拟,得到了不同工况下轴流泵内部不同监测点的水流压力脉动值规律。
前人对于轴流泵抽水时的稳定性研究较多,而对泵站反向运行的稳定性分析很少。本文通过对泵站流道进行全数值模拟,并对泵站正转反转工况下,在最优工况点时,在不同位置产生的压力脉动规律进行分析,研究泵反向发电时的稳定性问题。
2 数值模拟与试验
2.1 模型建立及网格划分
如图1所示,本文结合南水北调东线某泵站进行反向发电工况的数值模拟[9]。泵站机组基本参数如下:正反转运行转速均为150 r/min、设计扬程4.70 m,叶轮叶片为3片,安放角为-2°。
因轴流泵结构复杂,采用非结构网格对计算区域进行网格划分,对转轮部分及导叶部分进行加密。对网格进行无关性验证[10]后最终确定方案划分网格总数为250万,其中转轮体网格总数为103万,导叶体97万。

图1 流道整体图
2.2 基本控制方程
流体基本控制方程采用基于Reynolds平均的Navier-stokes方程[10],如公式(1)所示:

其中t为时间;ρm为混合项的密度;μt为湍流粘性系数;μm为动力粘性系数,按汽,液两相体积分数加权平均后获得;p为压力;u为速度矢量。
3 边界条件及试验
3.1 压力脉动监测点布置
如图1所示,在转轮进出口截面设2个监测面,两监测面距离为2.2 m。为研究监测面压力脉动分布规律,径向设置A1~A3,B1~B3三个监测点;周向设置A2,A4,A5及B2,B4,B5三个监测点,监测点分布如图2所示。

图2 监测面及监测点示意图
为研究转轮前后压力脉动规律,需进行非定常计算[11]。非定常计算以定常计算为初场,定常计算时设置动静交接面为冷结转子类型frozen rotor interface,非定常计算设置动静交接面为瞬态冻结转子类型transient rotor,转轮边界均采用压力进出口[12]。湍流模型选取为SSTk-ε,采用自动壁面函数,固体面设置为无滑移,湍流粘度项采用二阶迎风格式,在时间域上采用二阶全隐式进行离散[13],为确保进行压力脉动计算时非定常结果的稳定性,设置总的采样时间为10个周期,设置时间步长为0.001 s,收敛残差为10-5,选取计算最后2个周期各点监测数据分析压力脉动规律[14]。
3.2 试验验证
图3为河海大学水力机械多功能试验台,轴流泵反向发电试验在此进行。试验台按照《SL140-2006水泵模型及装置模型验收试验规程》进行设计与建造,试验综合不确定度≤0.4%。
在轴流泵转轮叶片安放角为0°时,采用现场试验及数值模拟的方法,通过不断改变流量得到水泵的外特性曲线(见图4)。总体看来试验结果与数值模拟结果误差较小,流量-扬程曲线及流量效率曲线与试验结果较好地吻合,2条曲线趋势保持一致,验证了数值模拟的准确性。

图3 试验台

图4 轴流泵外特性图
4 结果分析
4.1 压力脉动时域图分析
通过数值计算得到轴流泵处于水泵反向发电工况时内部各监测点压力脉动的时域信息[16]。为了消除监测点本身的静压对该点压力脉动的影响,在分析中引入无量纲的压力脉动系数CP,其表达式为
式中CP为无量纲的压力系数;Pi为监测点在某一时刻的静压值,单位Pa,Pave为一个转动周期内静压的平均值,单位Pa。
在水泵及水轮机两个工况下,对转轮前后的压力脉动规律进行时域图分析(见下页图5)。
图 5(a)和图 5(b)为水泵工况下,转轮进口截面径向和周向压力脉动时域图。B1,B2,B3沿轮缘至转轮轮毂分布,此时水流受转轮转动影响上吸,因受转轮转动的影响加剧及导叶与转轮间的动静干涉作用强烈,三点处压力脉动呈现周期性波动,在一个周期0.4 s内有三个明显的波峰波谷。因转轮边缘处间隙较小,水流变化剧烈,B1处为压力脉动值最大约为0.05,约为B3近轮毂处的5倍。B2,B4,B5为水流中间周向分布的三点,因水流流动比较均匀,三点压力脉动规律明显,幅值相近。图5(c)和图5(d)为水泵工况下,转轮出口截面径向和周向压力脉动时域图。A1,A2,A3沿轮缘至转轮轮毂分布。此时水流从转轮流出,仍受转轮转动影响,一个转轮周期内有三个明显的波峰波谷,三点压力脉动较转轮进口处明显增大,边缘处A1处水流压力脉动幅值约为转轮进口处的2倍。三点压力脉动幅值从边缘至轮毂逐渐减小,A1边缘处压力脉动幅值约为0.1,约为轮毂边缘处2倍。
图 5(e)和图 5(f)水轮机工况下,转轮进口截面径向和周向压力脉动时域图。B1,B2,B3沿轮缘至转轮轮毂分布,此时水流从原出水流道进入,三点压力脉动规律明显。因转轮边缘处及中部水流速度变化剧烈,中心处水流影响较小,反映在A1,A2压力脉动系数较大达0.06,约为A3处压力脉动系数为0.02的3倍。径向方面,水流从流道较平稳地进入转轮,受转轮转动影响,B2,B4,B5三点的压力脉动规律明显且压力脉动幅值接近。图5(g)和图5(h)水轮机工况下,转轮出口截面处径向和周向压力脉动时域图。水流经过转轮转动流出,径向方面,水流受转轮转动影响较大,转轮边缘处间隙水流变化剧烈,边缘处测点B1的压力脉动值进一步增大达0.15,转轮中部点B2压力脉动系数值达0.06,两点呈现周期性波动,转轮中心B3处压力脉动规律不明显。周向方面,水流较均匀地流出转轮,B2,B4,B5三点受转轮转动影响,周期性明显,三点压力脉动幅值接近约为0.06。
比较水泵及水轮机两工况压力脉动,出转轮截面水流各点压力脉动较进转轮截面压力脉动值增大,受转轮转动影响,水流在转轮边缘处速度变化大,压力脉动剧烈;受进出水流道设置限制,水轮机工况下水流的压力脉动较水泵工况下压力脉动值偏大。
4.2 压力脉动频域图分析
在水泵及水轮机两个工况下,对转轮前后的压力脉动规律进行频域图分析。
图 6(a)和图 6(b)为水泵工况下,转轮进口截面径向和周向压力脉动频域图。B1,B2,B3沿轮缘至转轮轮毂分布,B2,B4,B5三点在水流中间周向分布。从图中可以看出水流受转轮转动影响严重,压力脉动主要分布在低频区域,主频为转频7.5 Hz。轮缘B1处压力脉动系数值最大为0.15,从轮缘至轮毂依次减小。水流受转轮转动影响较均匀地上吸,B2,B4,B5 压力脉动系数幅值接近约为 0.06。图 6(c)和图6(d)为水泵工况下,转轮出口截面径向和周向压力脉动频域图。可以看出各监测点较转轮进口压力脉动系数增加,边缘处A1的压力脉动系数最大达0.32,周向方面A2.A4.A5三点压力脉动系数幅值约为0.16。受转轮转动影响,压力脉动主频仍为转频 7.5 Hz,次频为 2.5 Hz。
图 6(e)和图 6(f)水轮机工况下,转轮进口截面径向和周向压力脉动频域图,图6(g)和图6(h)为转轮出口截面处径向和周向压力脉动频域图。水流从原出水流道流入,进出口均受转轮转动影响,压力脉动主要集中在低频区域,主频为转频7.5 Hz,次频为转频2.5 Hz,在转频倍数处也有一定的压力脉动,并逐渐减小。进口截面压力脉动系数最大值出现转轮边缘处A1,值约为0.3,是转轮边缘A3处的3倍。出口截面压力脉动系数最大值出现在转轮边缘处B1,其值达0.8。周向方向,水流从转轮较均匀进入与流出,两监测面监测点的幅值大小接近,出转轮时各点的压力脉动系数幅值较进转轮时增大。
比较水泵及水轮机工况,受转轮转动影响强烈,各点的压力脉动频率分布在低频,主频为转频,出转轮时各点压力脉动幅值较进转轮时压力脉动幅值增大,水流在转轮间隙处变化剧烈,边缘处监测点压力脉动幅值较大。
5 结论

图5 压力脉动时域图
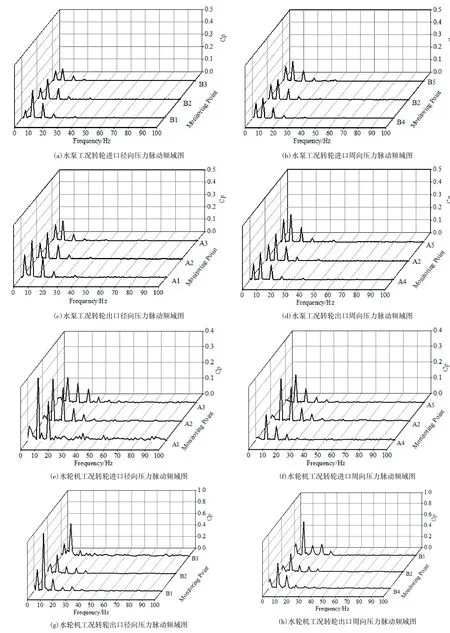
图6 压力脉动频域图
通过对南水北调苏北某泵站的机组轴流泵反向发电工况下的数值模拟,对机组反向发电稳定性进行了研究。
通过在导叶、转轮前后设置了径向与周向监测点,对轴流泵的内部运行的稳定性进行了模拟分析。水轮机工况下,压力脉动受转轮转动频率影响明显,压力脉动主频为转频;叶轮出口压力脉动大于叶轮进口处压力脉动,其压力脉动幅值约为进口处的2倍,压力脉动相对值从轮毂到轮缘处逐渐增大。比较水泵工况及水轮机工况下各点的压力脉动,水轮机工况下各监测点均高于水泵工况下各点压力脉动幅值,机组较水泵工况下振动增加,机组的不稳定性增加。
——“AABC”和“无X无X”式词语

