地下水DNAPLs污染修复多相流模拟的替代模型

侯泽宇,王 宇,卢文喜

地下水DNAPLs污染修复多相流模拟的替代模型

侯泽宇1,王 宇2*,卢文喜2

(1.吉林大学建设工程学院,吉林 长春 130000；2.吉林大学新能源与环境学院,吉林 长春 130021)

应用克里格法、支持向量回归法、核极限学习机法建立多相流模拟模型的替代模型,并应用集对分析法建立组合替代模型,通过将多种替代模型进行对比,分析不同替代模型在地下水DNAPLs污染修复多相流模拟问题中的适用性.结果表明,3种单一替代模型中,克里格模型的精度最高,其次是核极限学习机模型,最后是支持向量回归模型;应用集对分析原理建立集对权组合替代模型,与单一替代模型相比,其模拟模型的逼近精度更高,且提升效果十分显著,平均残差和平均相对误差分别为0.4009%和0.5373%;集对权组合替代模型运行一次仅需1.5s,选择组合替代模型代替多相流模拟模型进行地下水DNAPLs污染的修复方案优选分析,能够大幅减小模拟-优化过程的计算负荷,并保持较高的计算精度.

DNAPLs；地下水污染；修复方案设计；多相流模拟；组合替代模型

石油产品的生产过程中,由于泄露、偷排、意外事故等原因,造成生态污染并严重地威胁着人类健康[1].其中,密度大于水的重非水相流体(DNAPLs),具有高毒性、低水溶性和高界面张力的特性,常用的抽出处理修复技术对它难以奏效[2-4].表面活性剂冲洗技术,也称为表面活性剂强化含水层修复技术(SEAR),利用表面活性剂提高DNAPLs在水中的溶解性和迁移性,提高了抽出处理技术对于DNAPLs修复的有效性[5].然而,表面活性剂修复过程费用很高,为了控制成本,需要在修复之前制定合理高效的修复方案.

目前,运用模拟优化方法对含水层修复过程进行优化设计日益受到重视.在模拟-优化理论与方法的研究中,多相流数值模拟是重要的研究内容之一.自20世纪70年代开始,已有UTCHEM、COMSOL Multiphysics、T2VOC、Tough2等软件被广泛应用于地下水中DNAPLs污染物运移、表面活性剂强化含水层修复、CO2地质储存[6-10]等过程的多相流数值模拟.虽然多相流数值模拟的研究已经日趋成熟,但相较于单相水流的数值模拟,其复杂程度和求解计算时间显著增加.因此,优化模型求解过程反复多次调用多相流模拟模型所带来庞大的计算负荷严重制约了模拟-优化方法在实际应用中的可行性.为了解决这一问题,有些研究建立了多相流模拟模型的替代模型[11].

替代模型是模拟模型的近似替代,能够以很小的计算负荷逼近模拟模型的输入-输出关系,并保持较高的计算精度[12-13].Huang等[14],He等[15]建立了多项式回归(PR)替代模型[14-15];其他学者尝试建立了人工神经网络(ANN)替代模型[16-20],用以解决地下水污染修复方案优化设计和地下水污染源反演识别等问题;Zhao等[21],宋健等[22]研究将克里格法应用于模拟模型的替代建模,显著提高了模拟-优化迭代过程的计算效率;鞠磊[23]研究建立了自适应逐步优化的高斯过程替代模型.这些替代模型都可以大幅度减少优化模型求解计算过程中直接调用模拟模型所造成的大量计算负荷,但是不同方法具有不同的适用条件和优缺点,且不同替代模型对模拟模型的逼近精度差距明显.

针对地下水DNAPLs污染多相流模拟替代模型的研究现状和存在问题,本文分别应用支持向量回归(SVR)法、克里格(Kriging)法、核极限学习机(KELM)法建立多相流模拟模型(UTCHEM)的替代模型,并应用集对分析法建立组合替代模型,以充分发挥不同替代模型各自的长处和优势,提高替代模型对模拟模型的逼近精度.通过对比分析甄选出最为适合DNAPLs污染含水层修复方案优选问题的替代模型,为地下水高效修复提供理论依据和技术支撑.

1 研究方法

1.1 SVR法

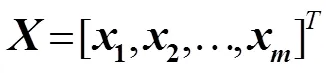
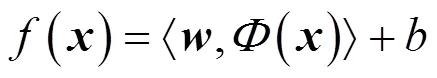
1.2 Kriging法

Kriging法的回归方程可以表示为[27-29]:

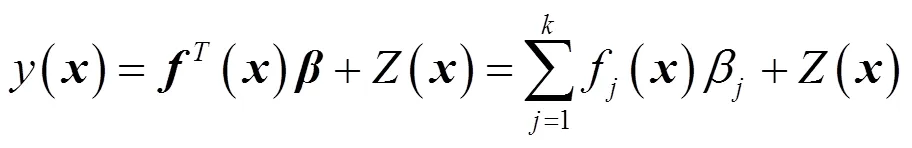
1.3 KELM法

KELM采用核映射替代传统极限学习机ELM中的随机映射,能够产生稳定的输出结果,其分类和拟合能力均优于非核的ELM方法.

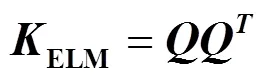
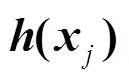
训练后的KELM输出函数表达如下[31]:

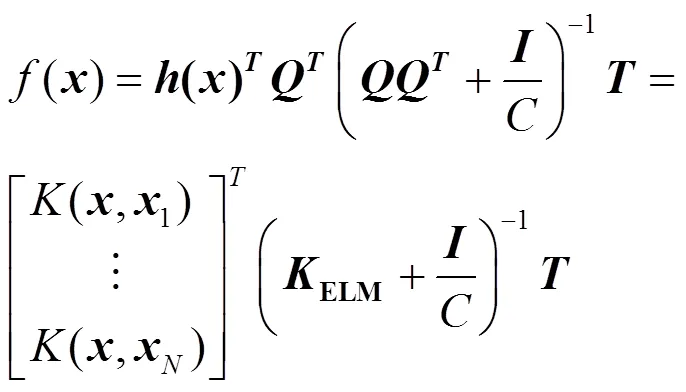
1.4 集对权组合替代模型

为了充分发挥不同单一替代模型各自的长处和优势,建立由多个单一替代模型构成的组合替代模型,以提高替代模型对模拟模型的逼近精度.

本文的组合替代模型包括两种类型:

第1种组合替代模型由Kriging替代模型、SVR替代模型及KELM替代模型加权线性叠加构成[32],其输出的表达式如下:

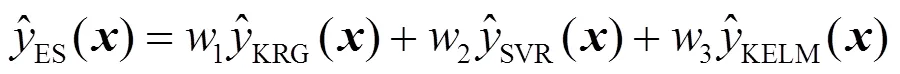
第2种组合替代模型由多个根据不同训练样本建立的同一种替代模型加权线性叠加构成,其输出的表达式如下:

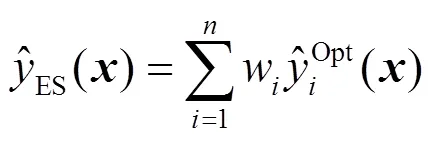
构造组合替代模型的一个关键环节是权重值的确定,替代模型的预测精度越高,其权重应越大;替代模型的精度越差,其权重应越小.本文选择集对分析(SPA)法作为权重的确定方法.

集对分析法能够从整体和局部上分析研究对象间的不确定性关系,从而对研究对象间联系的紧密程度(近似程度)做出全面且准确的评价[33].应用集对分析法建立组合替代模型的步骤可概括为:将利用同一组输入所获得的模拟模型的输出集合A和替代模型的输出集合B构造成集对H(A, B),并针对集对进行同异反定量比较分析.按替代模型输出与模拟模型输出间相对误差(绝对值)的大小将集对分为4类:1) 相同,其个数记为;2) 微小差异,其个数记为1;3) 明显差异,其个数记为2;4) 对立,其个数记为.替代模型与模拟模型之间的联系度可表示为[34-35]:

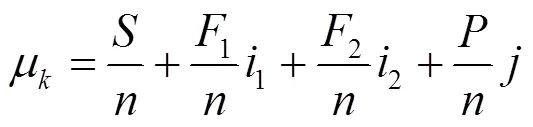
式中:1为微小差异系数;2为明显差异系数;为对立系数.通常情况下,系数1,2,分别取0.5,-0.5和-1.根据不同替代模型与模拟模型之间联系度的大小,可计算各替代模型对应的集对权重.

2 应用研究

2.1 问题描述

本文针对假想的污染场地,建立三维多相流数值模拟模型来模拟SEAR过程.某化工厂发生爆炸,导致大量以硝基苯为主的有机化合物泄露,严重污染了附近的地下水.污染质经过12d的泄露和105d的自由扩散.

根据污染质的分布情况,建立包含7口注水井和1口抽水井的表面活性剂强化修复系统,表面活性剂选用十二烷基苯磺酸钠(SDBS).抽水井为设定于污染晕中心位置的完整井,注水井为非完整井,1口布设在污染质泄露位置的上方向下冲刷污染质,其他布设在含水层底部污染晕四周(图1).为了使表面活性剂与硝基苯充分地混合反应,也尽可能地清洗残余的表面活性剂和硝基苯,在表面活性剂冲洗之后,需要进行注水冲洗直至污染物去除率满足要求.抽、注水量与表面活性剂冲洗阶段保持一致.为了保持地下水量平衡,抽水总量与注水总量相等.

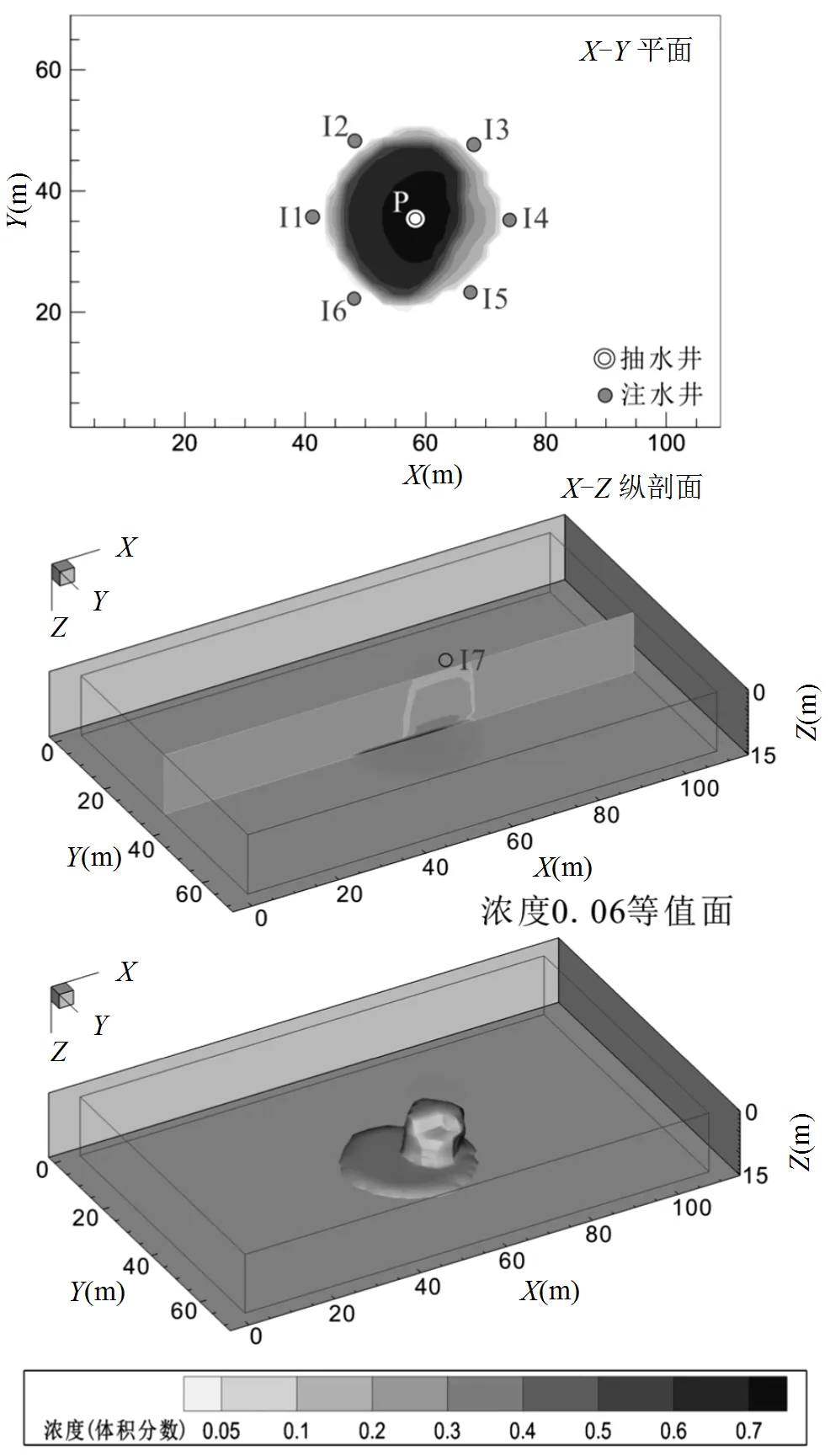
图1 污染物分布及抽注水井布设

2.2 模拟模型的建立

计算目的层为松散岩类孔隙潜水含水层,研究区可概化为非均质、各向同性,并含有若干夹层的三维多相流模型.污染场地附近无天然边界,在受修复过程影响和污染物迁移影响可忽略不计的地段划定边界.其中,东西边界概化为一类边界,地下水流向由东向西,水力梯度为0.0112;南北边界由流面组成,概化为零通量边界;计算模拟区的上部为潜水面,是水量交换边界,下部为隔水层,可概化为零通量边界(图2).含水层渗透率的分布如图3所示,其他含水层参数及物理化学参数在表2中列出.由于研究对象为假想,研究过程省去了模型的校正与检验.

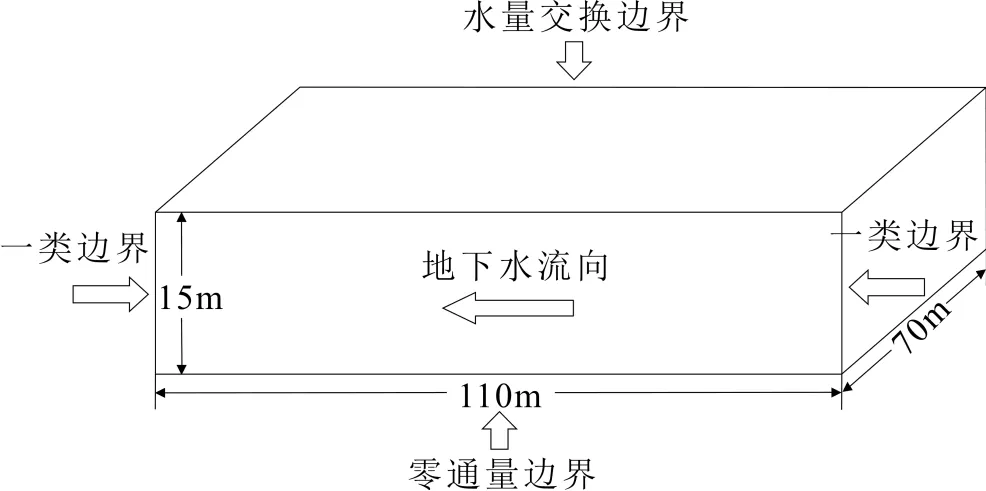
图2 计算区以及相应的边界条件

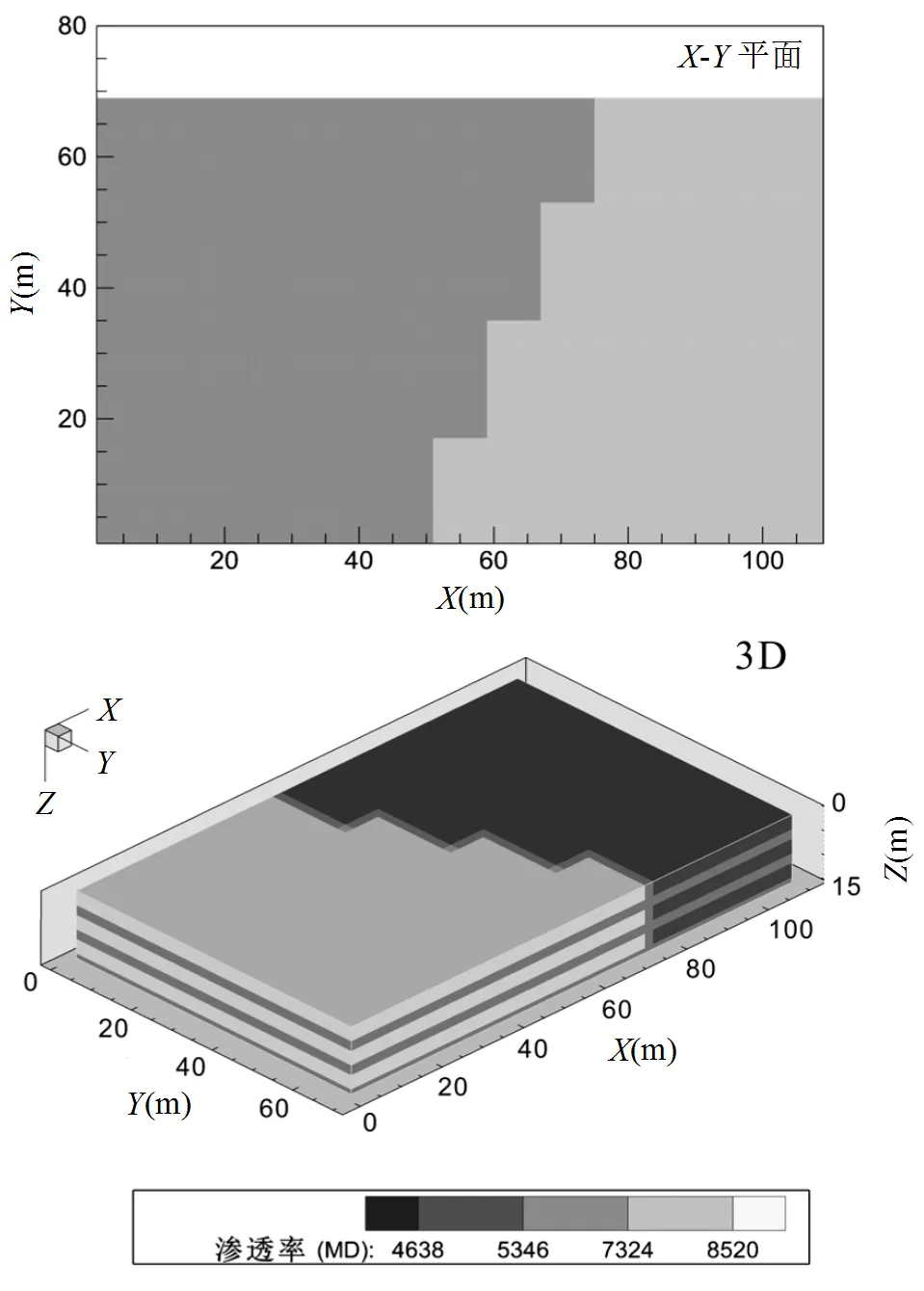
图3 渗透率分布

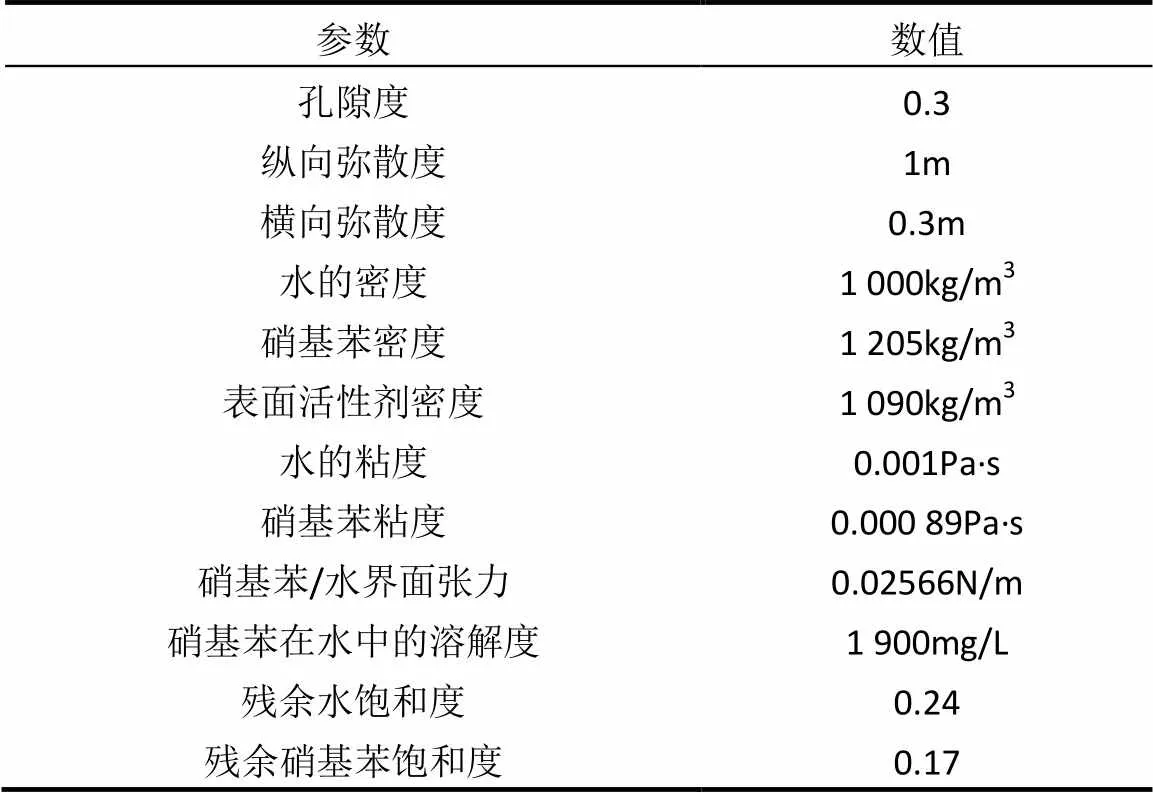
表1 硝基苯污染含水层参数及物理化学参数

根据污染场地的水文地质概念模型,初步建立如下多相流数学模型:

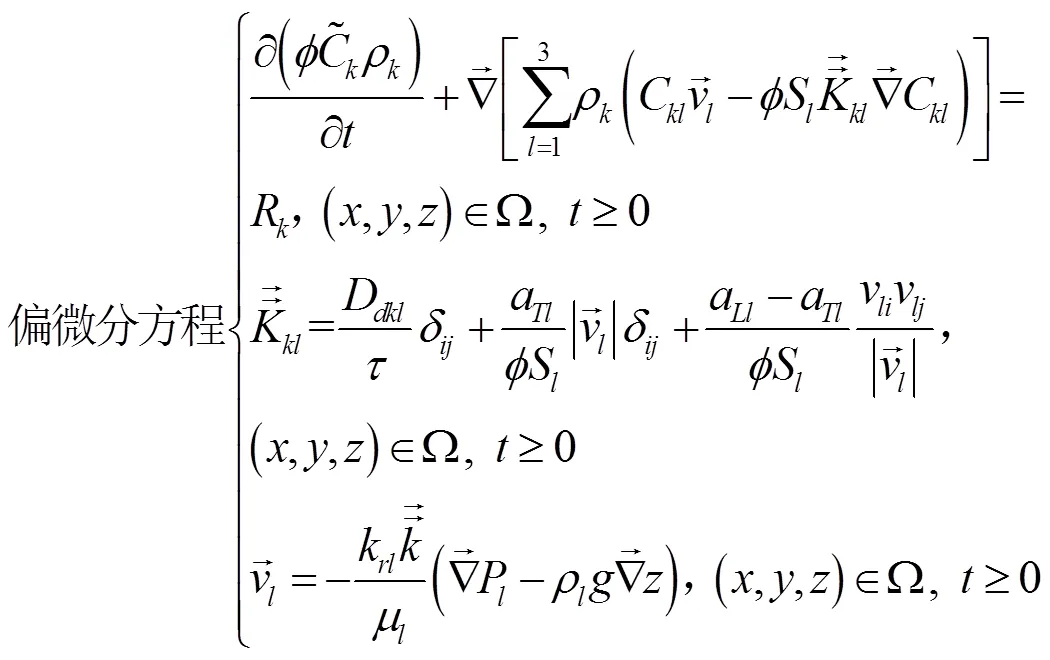
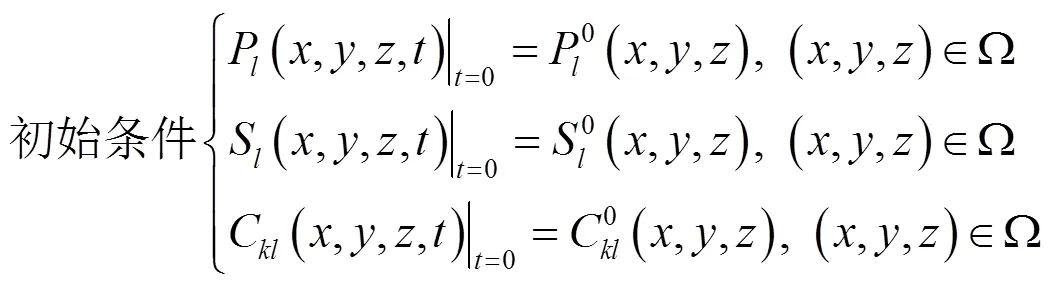
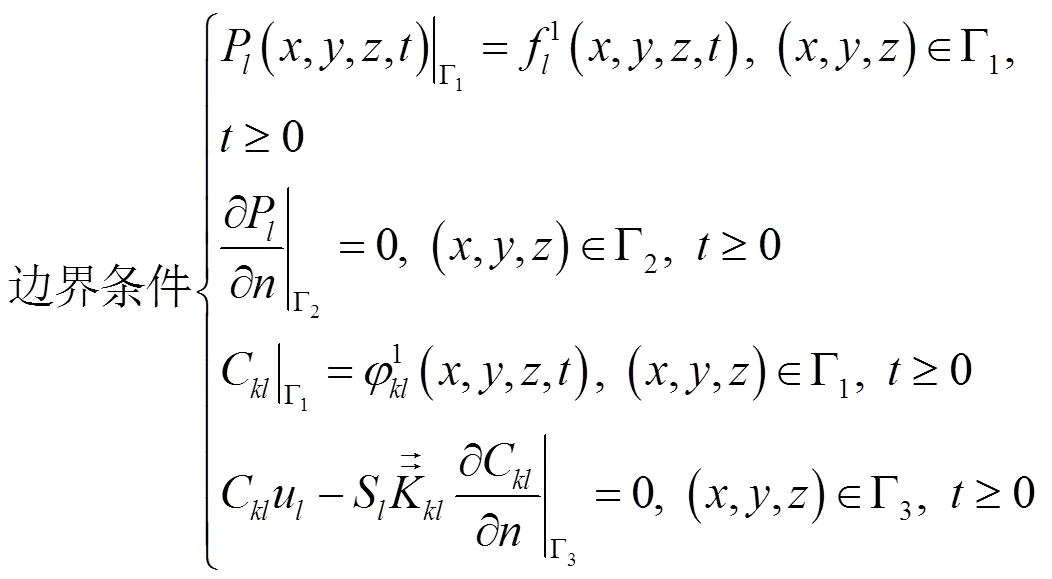
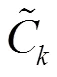
2.3 替代模型的建立及检验

Luo等[36]运用Sobol’全局敏感性分析发现,修复时间以及总抽水量对修复效果的影响较大,而表面活性剂浓度在合理范围内变化对修复效果影响较小.借鉴其研究结果,将表面活性剂浓度固定为4%,以各注水井的抽水量(总抽水量等于各注水井注水量的和)、修复时间作为优化的可控输入变量建立替代模型.为了减小输入向量的维度以提升替代模型的精度,本文使相对的两个注水井的注水量相等,抽水井的抽水量等于注水量的总和.同时,增加水冲洗时间、水冲洗阶段抽注水量并不会明显提高污染质的去除率,所以可将水冲洗时间固定为25d,抽、注水量与表面活性剂冲洗阶段保持一致.最终,替代模型的输入向量由5个要素组成:注水井I1、I2、I3、I7的注水量和表面活性剂冲洗时间.输出变量为硝基苯去除率.

本文设计的集对加权组合替代模型需要4个由不同训练样本建立独立的替代模型,故需要进行6次拉丁超立方抽样,每次抽样获得50个样品点,4组作为训练样本,2组作为检验样本.训练样本用来建立替代模型,而检验样本由不同于训练样本的样品点组成,用来检验替代模型对模拟模型的逼近精度.各输入变量在取值范围内均服从均匀分布.为了使抽样点更均匀地覆盖变量的取值范围,抽样时抽取子区间的左端点值或中间值.抽样结束后,将样本方案输入多相流模拟模型,获得相应的输出(硝基苯去除率),最终构成用于建立替代模型的训练及检验样品数据集.

为了对比由SVR法、Kriging法、KELM法建立的替代模型对多相流模拟模型的逼近程度,本文以训练样本①、③中的100个训练样品建立替代模型,并应用100个检验样品对3个替代模型的精度进行检验.

3种替代模型的训练和检验在MATLAB平台上完成, Kriging模型、KELM模型为自编程序, SVR模型采用Libsvm工具箱[37].3种替代模型的参数取值如表2所示.根据训练样本对3种替代模型进行5折交叉验证,由粒子群优化算法计算各模型的最优参数,使得交叉验证过程中,替代模型输出与模拟模型输出之间的拟合误差之和最小.

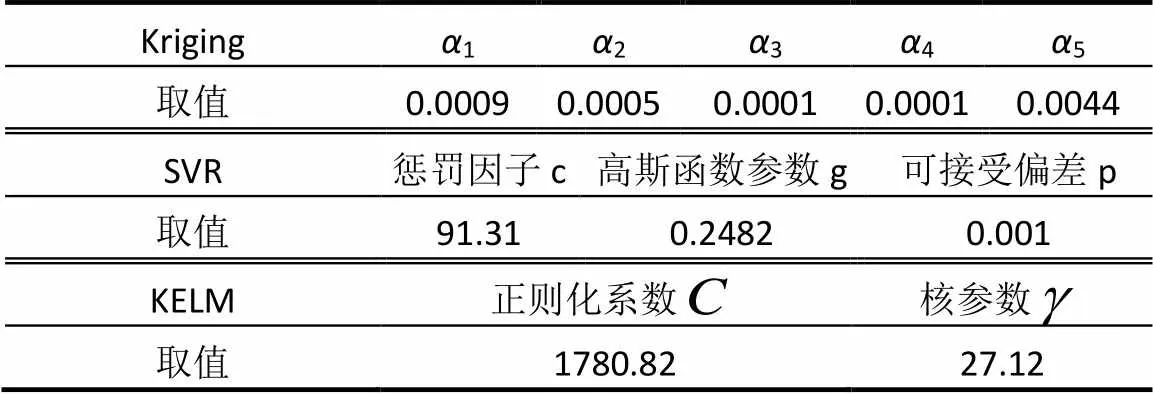
表2 替代模型参数

将检验样本中的100个修复方案输入训练好的替代模型,获得输出响应(硝基苯去除率),并将其与多相流模拟模型的输出响应对比,对比结果如图4所示.结果表明:三种替代模型都对模拟模型有较高的逼近精度,对比结果接近1:1完美线,能够识别并取代模拟模型的输入-输出关系.其中, Kriging模型的对比结果最接近1:1完美线.

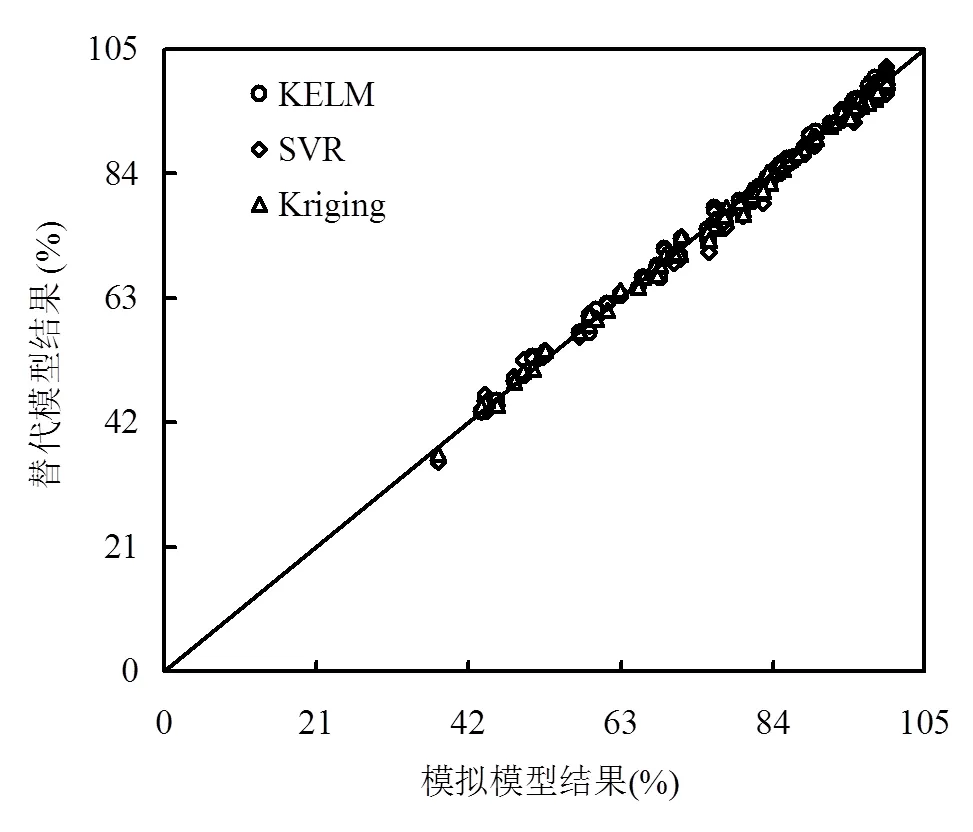
图4 替代模型结果与模拟模型结果拟合

表3 单一替代模型精度分析

采用确定性系数(2)、最大残差(绝对误差)、平均残差(绝对误差)、最大相对误差和平均相对误差5个指标,评估替代模型对模拟模型的逼近精度[38].3个替代模型的各项精度评估指标对比情况如表3所示, Kriging模型的各项指标均明显优于其他替代模型, KELM模型次之,最后为SVR模型,说明Kriging模型对多相流模拟模型的逼近精度最高.因此,确定Kriging法为地下水DNAPLs污染修复方案优选问题中最优的替代模型建模方法,将被应用于第二种组合替代模型的建模.

2.4 组合替代模型的建立及检验

集对权组合替代模型1:以建好的Kriging模型、SVR模型、KELM模型作为集对权组合替代模型1的子模型.将子模型的输出分别与模拟模型的输出构成集对,按残差的大小(绝对值)将集对分为4类:残差小于0.3%的为相同,残差在0.3%~0.6%之间的为差异一,残差在0.6%~1%之间的为差异二,残差大于1%的为对立.根据分类结果可计算各子模型的集对权重,分别为0.5250、0.3500和0.1250.最终,集对权组合替代模型的输出为各子模型输出的加权和.

集对权组合替代模型2:将拉丁超立方抽样获得4个训练样品组两两组合,构成4个样本容量为100的训练样本:①③、①④、②③、②④.运用Kriging法建立4个替代模型作为集对权组合替代模型2的子模型.将子模型的输出分别与模拟模型的输出构成集对,根据集对分类结果可计算各子模型的集对权重, 分别为0.2234、0.3670、0.1915和0.2181.对于同一种替代模型而言,训练样本发生改变,预测精度也会发生明显的变化.最终,集对加权组合替代模型的输出为各子模型输出的加权和.

将集对权组合替代模型的输出结果与其他替代模型进行对比来分析其精度.为了更充分地说明集对权组合替代模型对于精度的提升,在对比对象中加入以所有训练样品(200个训练样品)建立的Kriging替代模型,对比结果如表4、图5、图6所示.由图5可知,集对加权组合替代模型2结果的残差在小值区间分布的个数明显多于其它模型;由表5和图6可知,2种集对权组合替代模型中,组合模型2更有效地降低了残差水平,平均残差和平均相对误差分别只有0.4009%和0.5373%;此外,组合模型2能够避免个别输出残差过大的情况,最大残差和最大相对误差分别被缩小到1.4279%和2.5493%,很大程度地提高了替代模型的可靠性,其精度高于其它所有参与比较的替代模型,包括组合模型1和应用所有训练样品建立的Kriging替代模型.而组合模型1并未取得较好的提升逼近精度的效果,其部分精度指标甚至低于单一的Kriging替代模型.

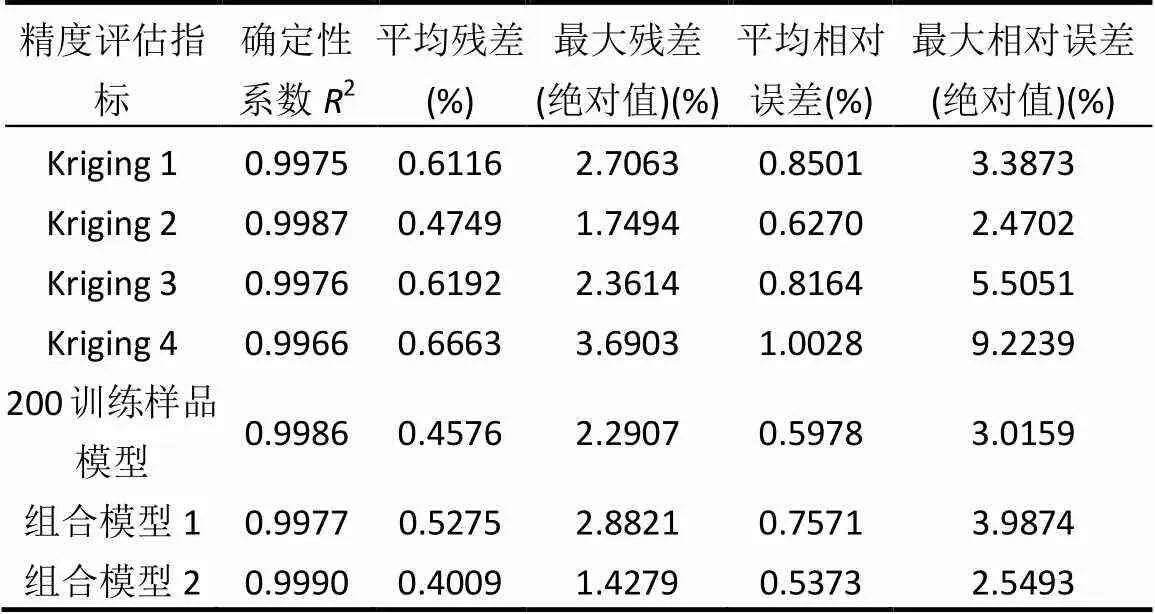
表4 替代模型精度分析

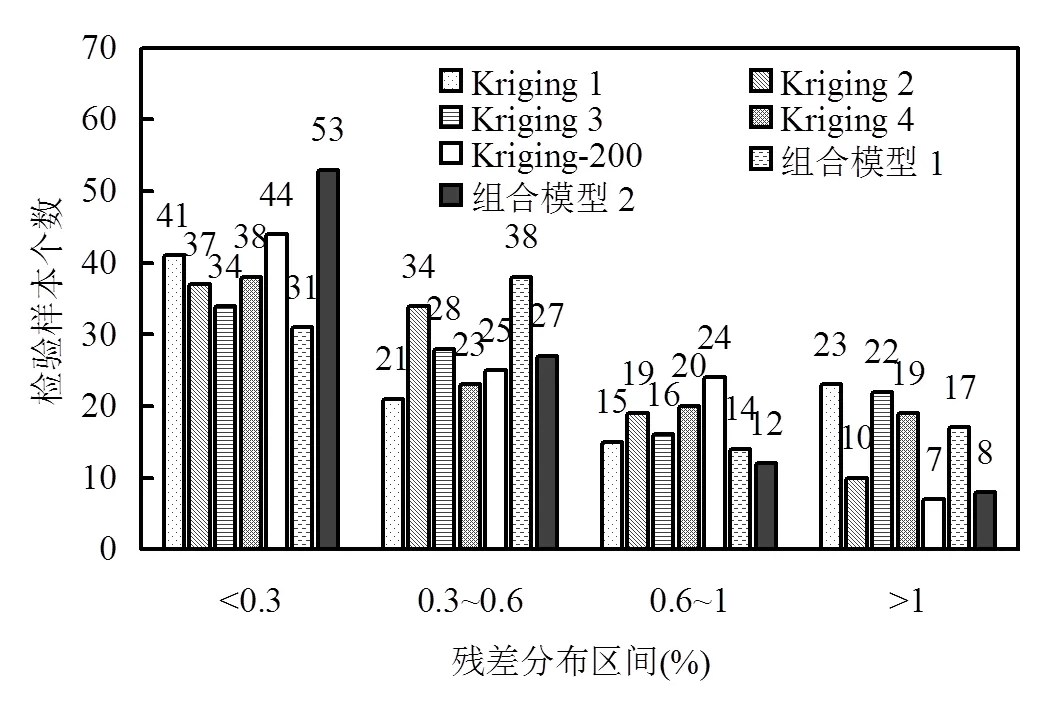
图5 替代模型残差分布

通过以上研究可知:1.两种组合替代模型的建模方式中,将根据不同训练样本建立的多个Kriging模型组合,可以获得精度更高的组合替代模型,优于根据同一组训练样本应用不同方法建立的组合替代模型;2.将训练样本拆分成多组,建立多个单一替代模型,进而构建组合替代模型,其精度高于应用全部训练样品建立的单一替代模型;3.应用集对分析原理建立组合替代模型十分必要,能够显著提升替代模型对模拟模型的逼近精度.

模拟、优化方法的主要计算负荷来自于反复多次调用模拟模型.该硝基苯污染含水层多相流数值模拟模型在CPU为Intel core i5 3.0GHz内存为8GB的计算机上运行一次平均需要大约600s.如果用传统的模拟-优化方法来解决修复方案的优选问题,模拟模型需要运行超过15000次,花费约104d时间.

集对权组合替代模型运行一次需要1.5s,如果将KELM模型引入模拟-优化模型中来代替模拟模型,在满足平均残差0.4009%的条件下,优化求解过程减少到只需要6h.因此,替代模型的引入在保证精度的同时大大减小了整个计算过程的计算负荷.

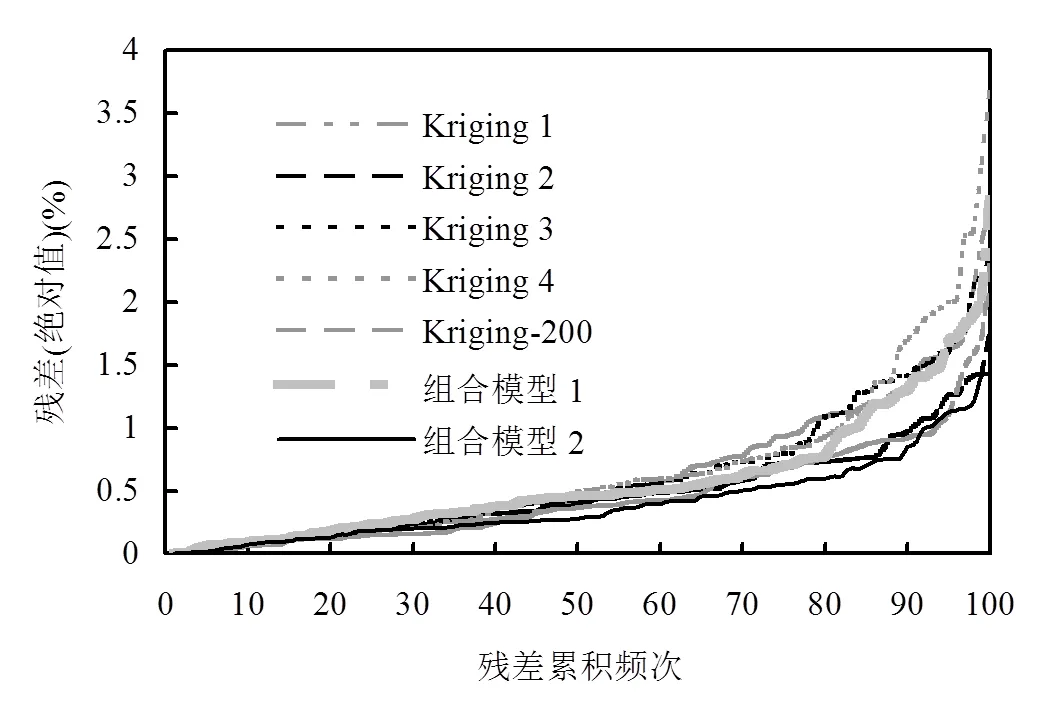
图6 替代模型残差累积频率曲线

3 结论

3.1 Kriging模型、SVR模型以及KELM模型3种替代模型对多相流模拟模型都有较好的逼近精度,其中Kriging模型的精度最高, KELM模型次之,最后是SVR模型.

3.2 应用集对分析原理建立集对权组合替代模型,与单一替代模型相比,其拥有对模拟模型更高的逼近精度,而且提升效果十分显著,平均残差和平均相对误差分别只有0.4009%和0.5373%.

3.3 两种组合替代模型的建模方式中,将根据不同训练样本建立的多个Kriging模型组合,可以获得精度更高的组合替代模型,明显优于根据同一组训练样本应用不同方法建立的组合替代模型.两种组合模型的最大残差分别为1.4279%和2.8821%

3.4 如果应用模拟-优化方法进行地下水DNAPLs污染的修复方案优选分析,选择集对权组合替代模型代替多相流模拟模型能够大幅度地减小模拟-优化过程的计算负荷,并保持较高的计算精度.

[1] Fernández-Garcia D, Bolster D, Sanchez-Vila X, et al. A Bayesian approach to integrate temporal data into probabilistic risk analysis of monitored NAPL remediation [J]. Advances in Water Resources, 2012,36:108-120.

[2] Fetter C W. Contaminant hydrogeology (second edition) [D]. New York: Macmillan Publishing Company, 1999.

[3] 王 锐.非水相流体在土壤中运移规律研究[D]. 西安:西北农林科技大学, 2004. Wang R. Experimental study on nonaqueous phase liquids transport in soils [D]. Xi-an: Northwest Sci-Tech University of Agriculture and Forestry, 2004.

[4] Falta R W, Suresh Rao P, Basu N. Assessing the impacts of partial mass depletion in DNAPL source zones: Ⅰ. Analytical modeling of source strength functions and plume response [J]. Journal of Contaminant Hydrology, 2005,78(4):259-280.

[5] Qin X S, Huang G H, Chakma A, et al. Simulation-based process optimization for surfactant-enhanced aquifer remediation at heterogeneous DNAPL-contaminated sites [J]. Science of the Total Environment, 2007,381(1-3):17-37.

[6] Delshad M, Pope G A, Sepehrnoori K. A compositional simulator for modeling surfactant enhanced aquifer remediation, 1. formulation [J]. Journal of Contaminant Hydrology, 1996,23(4):303-327.

[7] 秦梓钧,刘保君,张 雪,等. COMSOL Multiphysics有限元软件数值模拟气液两相流的可行性研究[J]. 当代化工, 2016,45(5):916-919. Qin Z J, Liu B J, Zhang X, et al. Study on the feasibility of using COMSOL Multiphysics software in numerical simulation of gas-liquid two-phase flow [J]. Contemporary Chemical Industry, 2016, 45(5):916-919.

[8] 张 蔚.渗透率空间变异性对重非水相液体运移影响的数值模拟[D]. 南京:南京大学, 2013. Zhang W. Impact of the spatial variation of permeability on the transport fate of dense non-aqueous phase liquids [D]. Nanjing: Nanjing University, 2013.

[9] 郑 菲.典型DNAPLs在饱和多孔介质中的运移及修复研究[D]. 南京:南京大学, 2015. Zheng F. Investigation on the migration and remediation of typical DNAPLs in saturated porous media [D]. Nanjing: Nanjing University, 2015.

[10] Biagi J, Agarwal R, Zhang Z M. Simulation and optimization of enhanced gas recovery utilizing CO2[J]. Energy, 2016,94:78-86.

[11] Lu W X, Chu H B. Optimization of denser nonaqueous phase liquids-contaminated groundwater remediation based on Kriging surrogate model [J]. Water Practice & Technology, 2013,8(2):304-313.

[12] Asher M J, Croke B F W, Jakeman A J, et al. A review of surrogate models and their application to groundwater modeling [J]. Water Resources Research, 2015,51(8):5957-5973.

[13] 侯泽宇.地下水DNAPLs污染源反演识别及不确定性分析研究[D]. 长春:吉林大学, 2018. Hou Z Y. Source identification and uncertainty analysis for DNAPLs-contaminated groudwater [D]. Changchun: Jilin University, 2018.

[14] Huang Y F, Li J B, Huang G H, et al. Integrated simulation optimization approach for real-time dynamic modeling and process control of surfactant-enhanced remediation at petroleum- contaminated sites [J]. Practice Periodical of Hazardous, Toxic, and Radioactive Waste Management, 2003,7(2):95-105.

[15] He L, Huang G H, Zeng G M, et al. An Integrated simulation, inference, and optimization method for identifying groundwater remediation strategies at petroleum-contaminated aquifers in western Canada [J]. Water Research, 2008,42(10/11):2629-2639.

[16] Rao S V N. A computationally efficient technique for source identification problems in Three-Dimensional Aquifer Systems using neural networks and simulated annealing [J]. Environmental Forensics, 2006,7(3):233-240.

[17] Mirghani B Y, Zechman E M, Ranjithan R S. Enhanced simulation– optimization approach using surrogate modeling for solving inverse problems [J]. Environmental Forensics, 2012,13(4):348-363.

[18] Luo J N, Lu W X, Xin X, et al. Surrogate model application to the identification of an optimal surfactant-enhanced aquifer remediation strategy for DNAPL-contaminated sites [J]. Journal of Earth Science, 2013,24(6):1023-1032.

[19] Srivastava D, Singh R M. Breakthrough curves characterization and identification of an unknown pollution source in groundwater system using an artificial neural network (ANN) [J]. Environmental Forensics, 2014,15(2):175-189.

[20] Srivastava D, Singh R M. Groundwater system modeling for simultaneous identification of pollution sources and parameters with uncertainty characterization [J]. Water Resources Management, 2015, 29:4607-4627.

[21] Zhao Y N, Lu W X, Xiao C N. A Kriging surrogate model coupled in simulation-optimization approach for identifying release history of groundwater sources [J]. Journal of Contaminant Hydrology, 2016,185: 51-60.

[22] 宋 健,吴剑锋,杨 蕴,等.基于含水层DNAPL污染修复替代模型的多目标优化研究[J]. 中国环境科学, 2016,36(11):3390-3396. Song J, Wu J F, Yang Y, et al. A Kriging-based surrogate model for multi-objective optimization of DNAPL-contaminated aquifer remediation [J]. China Environmental Science, 2016,36(11):3390- 3396.

[23] 鞠 磊.基于多源数据同化的含水层异质性刻画[D]. 杭州:浙江大学, 2018. Ju L. Characterization of aquifer heterogeneity based on multi-source data assimilation [D]. Hangzhou: Zhejiang University, 2018.

[24] Zhang Y S, Kimberg D Y, Coslett H B, et al. Multivariate lesion- symptom mapping using support vector regression [J]. Human Brain Mapping, 2014,35(12):5861-5876.

[25] Smola A J, Scholkopf B. A tutorial on support vector regression [J]. Statistics and Computing, 2004,14(3):199-222.

[26] Hou Z Y, Lu W X, Xue H B, et al. A comparative research of different ensemble surrogate models based on set pair analysis for the DNAPL- contaminated aquifer remediation strategy optimization [J]. Journal of Contaminant Hydrology, 2017,203:28-37.

[27] Hou Z Y, Lu W X, Chu H B, et al. Selecting parameter-optimized surrogate models in DNAPL-contaminated aquifer remediation strategies [J]. Environmental Engineering Science, 2015,32(12):1016- 1026.

[28] 王 涵,卢文喜,李久辉,等.地下水DNAPLs污染多相流的随机模拟及其不确定性分析[J]. 中国环境科学, 2018,38(7):2572-2579. Wang H, Lu W X, Li J H, et al. Stochastic simulation and uncertainty analysis of multi-phase flow of groundwater polluted by DNAPLs [J]. China Environmental Science, 2018,38(7):2572-2579.

[29] 范 越,卢文喜,欧阳琦,等.基于Kriging替代模型的地下水污染监测井网优化设计[J]. 中国环境科学, 2017,37(10):3800-3806. Fan Y, Lu W X, Ouyang Q, et al. Optimum design of groundwater pollution monitoring well network based on Kriging surrogate model [J]. China Environmental Science, 2017,37(10):3800-3806.

[30] 姜 雪. DNAPLs污染含水层修复方案优选及不确定性分析[D]. 长春:吉林大学, 2016. Jiang X. Optimization and uncertainty analysis of DNAPLs contaminated aquifer repair scheme [D]. Changchun: Jilin University, 2016.

[31] Hou Z Y, Lu W X. Comparative study of surrogate models for groundwater contamination source identification at DNAPL- contaminated sites [J]. Hydrogeology Journal, 2018,26:923-932.

[32] Müller J, Shoemaker C A. Influence of ensemble surrogate models and sampling strategy on the solution quality of algorithms for computationally expensive black-box global optimization problems [J]. Journal of Global Optimization, 2014,60(2):123-144.

[33] 王文圣,向红莲,李跃清,等.基于集对分析的年径流丰枯分类新方法[J]. 四川大学学报(工程科技版), 2008,40(5):1-6. Wang W S, Xiang H L, Li Y Q, et al. A new approach to annual runoff classification based on set pair analysis [J]. Journal of Sichuan University (Engineering Science Edition), 2008,40(5):1-6.

[34] Cao Q K, Li L J, Yu B. Application of dynamic set-pair analysis in coal and gas outburst prediction [J]. Journal of Coal Science and Engineering (China), 2008,14(1):77-80.

[35] Wang W S, Jin J L, Ding J, et al. A new approach to water resources system assessment-set pair analysis method [J]. Science in China Series E: Technological Sciences, 2009,52(10):3017-3023.

[36] Luo J N, Lu W X. Sobol’ sensitivity analysis of NAPL-contaminated aquifer remediation process based on multiple surrogates [J]. Computers & Geosciences, 2014,67:110-116.

[37] Chang Chih-Chung, Lin Chih-Jen. LIBSVM: a library for support vector machines [EB/Z]. Software available at http://www.csie.ntu. edu.tw/~cjlin/libsvm. Accessed on December 22, 2016.

[38] 罗建男.基于替代模型的DNAPLs污染含水层修复方案优选[D]. 长春:吉林大学, 2014. Luo J N. Optimization of remediation strategy of DNAPLs- contaminated aquifer based on surrogate [D]. Changchun: Jilin University, 2014.

致谢：本次研究由吉林大学卢文喜教授指导完成,在此表示感谢.同时感谢期刊编辑与审稿专家的耐心修改与宝贵建议.

Surrogate models of multi-phase flow simulation model for DNAPL-contaminated aquifer remediation.

HOU Ze-yu1, WANG Yu2*, LU Wen-xi2

(1.College of Construction Engineering, Jilin University, Changchun 130000, China；2.College of New Energy and Environment, Jilin University, Changchun 130021, China)., 2019,39(7)：2913~2920

Kriging, support vector regression (SVR), kernel extreme learning machine (KELM) were applied to building the surrogate models of multi-phase flow simulation model, and set pair analysis (SPA) was applied to building ensemble surrogate models. The applicability of different surrogate models was analyzed via a comparison study. kriging model was with the highest accuracy, followed by KELM model and SVR model. Compared with Kriging model, set pair weighted ensemble surrogate model significantly improved the approximation accuracy. The mean of residuals and the mean of relative errors between ensemble model outputs and simulation model outputs were only 0.4009% and 0.5373%, respectively. Furthermore, it only took 1.5s to run the set pair weighted ensemble surrogate model. Replacing the simulation model with an ensemble surrogate model considerably reduced the computational burden of the simulation-optimization process and maintained high computation accuracy for optimizing the DNAPL-contaminated aquifer remediation strategy.

DNAPLs；groundwater contamination；remediation strategy optimization；multi-phase flow simulation；ensemble surrogate model

X523

A

1000-6923(2019)07-2913-08

侯泽宇(1989-),男,河北唐山人,博士后,主要从事地下水污染控制与修复研究.发表论文20余篇.

2018-12-04

国家自然科学基金资助项目(41672232,41807155);中国博士后科学基金资助项目(2018M641780)

* 责任作者, 讲师, chair19881224@126.com