中小尺度流域洪水模型模拟比较研究
王 婕,宋晓猛,张建云,王国庆,刘 晶
(1.中国矿业大学 资源与地球科学学院,江苏 徐州 221116;2.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,南京 210029;3.水利部应对气候变化研究中心,南京 210029)
0 引 言
在气候变化日益复杂的今天,洪涝灾害发生的频率和强度也在不断增大[1,2]。作为一项有效的防洪非工程措施,洪水预报在防汛工作中发挥着巨大的作用,因此,洪水预报技术的不断提高显得愈发重要。在现代洪水预报调度中,关键部分就是流域水文模型的应用,各类水文模型在水循环模拟中考虑的侧重点不同,造成了模拟结果间的差异[3-7]。国内学者比较了不同模型间结果的差异,如刘佩瑶等[8]应用新安江模型和改进后的神经网络模型在闽江进行水文预报,发现基于LM算法的网络模型模拟效果明显优于新安江模型;张汉辰等[9]对比了CASC2D与新安江模型的应用结果,发现在前毛庄流域效果相近,在前板桥流域新安江模型效果略优;王思媛等[10]比较了HBV模型和新安江模型在黄河源区的应用,发现GA算法率定下的新安江模型模拟效果优于HBV模型。此外,宋晓猛[11]、阚光远[12]等则将新安江模型和人工神经网络模型进行耦合应用,模型模拟效果均获得改善。目前研究大多集中在同类模型的比较,对不同类型模型的比较相对欠缺。
本文利用新安江模型(集总式模型)、TOPMODEL模型(半分布式水文模型)、人工神经网络模型(数据驱动模型)3种不同类型模型的基本原理及结构,以沿渡河流域为例,进行次洪过程模拟和对比研究,分析比较各模型模拟结果的优劣及地区适用性,为洪水预报方案的完善与选择提供前期的模型数据支持。
1 资料与方法
1.1 流域概况
沿渡河流域位于长江上游支流(110°05′E~110°30′E,31°10′N~31°30′N),流域面积601 km2。流域内多山地,植被茂密,属典型的季风气候,年均气温在11.5 ℃左右,年均降水量为1 650 mm左右,汛期为每年5-9月。流域内分布有5个雨量站,沿渡河流域水系及测站分布图如图1所示。
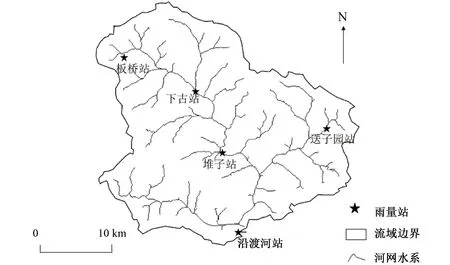
图1 沿渡河流域水系及测站分布Fig.1 Drainage networks and observational station distribution
本文利用沿渡河流域1981-1987年30场历史洪水资料进行次洪模拟,其中降雨径流及其他水文气象数据均来源于流域测站观测资料。挑选18场代表性洪水作为率定场次,其余12场作为验证场次。
1.2 新安江模型
新安江模型是一个集中性概念式的流域水文模型,以蓄满产流为基础,主要由四个模块构成,分别是产流计算、蒸发计算、水源划分和汇流计算,模型计算流程如图2所示[13]。
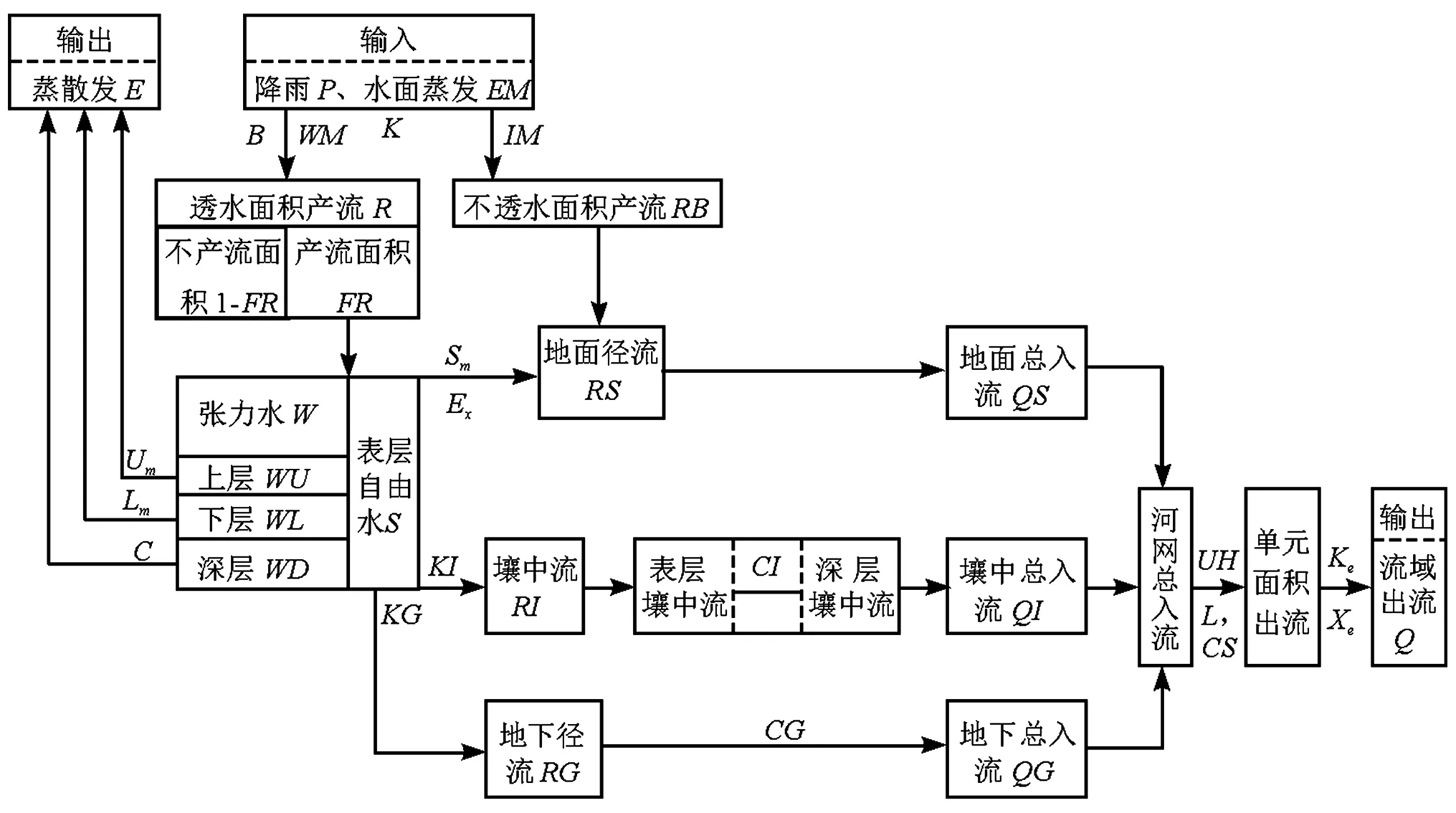
图2 新安江模型(三水源)计算流程图Fig.2 Framework of the Xin'anjiang Model (three runoff components)
本文应用的模型参数共有16个,其中产流计算参数10个:蒸发折算系数(K),蓄水容量曲线的方次(B),流域平均蓄水容量(WM),上层蓄水容量(WUM),下层蓄水容量(WLM),深层蒸散发系数(C),自由水蓄水容量(SM),自由水蓄水容量曲线的方次(EX),自由水蓄水库补充地下水的出流系数(KG),自由水蓄水库补充壤中流的出流系数(KI);汇流计算参数6个:地下水库消退系数(CG),壤中流消退系数(CI),地表消退系数(CS),单元河段的马斯京根模型参数K值(Ke)和X值(Xe),滞后演算参数(L)。
1.3 TOPMODEL
TOPMODEL是基于变动产流概念半分布式流域水文模型,考虑了流域地形地貌、土壤、地下水等影响因子,其计算包括地形指数计算、产流计算、汇流计算,模型计算流程图如图3所示[14]。
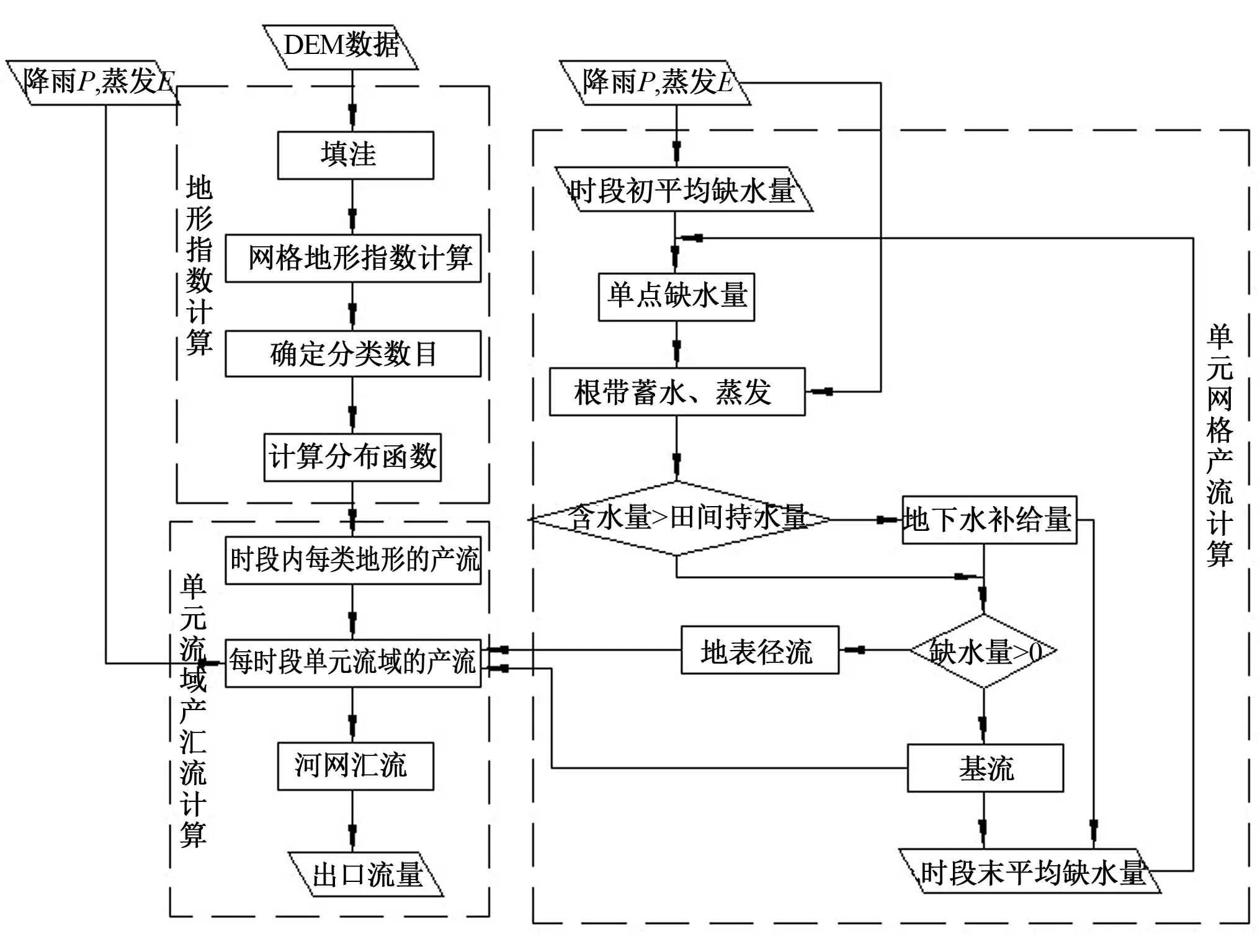
图3 TOPMODEL计算流程图Fig.3 Framework of the TOPMODEL model
TOPMODEL共有参数5个:土壤下渗率以指数形式降低的速率参数(m),刚达到饱和状态时的土壤有效传导率的自然对数ln(T0),根带最大蓄水能力(SRmax),初始缺水量(SRinit),地表汇流的有效速度(Chvel)。
1.4 BP模型
BP模型是具有多层网络,且可以逆序传递修正降低误差的一种前馈神经网络[15]。本文构建的BP模型结构为8-17-1(输入层-隐含层-输出层),其结构图如图4所示。图中P代表降水,Q代表流量,N代表与模拟仿真函数相关的隐含层节点。
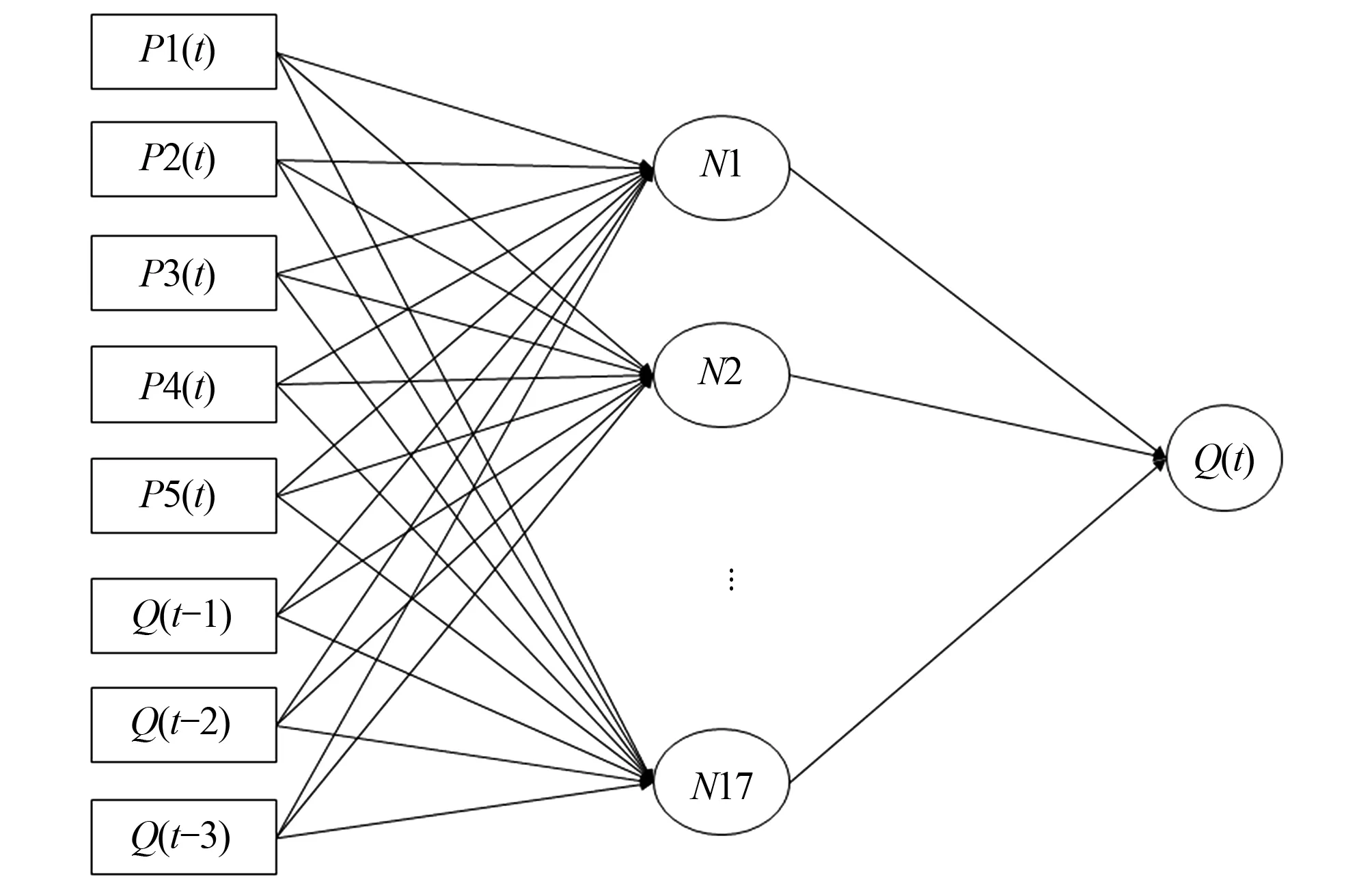
图4 BP模型结构图Fig.4 BP model flowchart
1.5 评价目标函数
选择纳什效率系数、相对误差及峰现时刻误差为目标函数进行模型参数率定,目标函数计算公式如下:
(1)
(2)
ΔT=T实测-T模拟
(3)
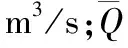
采用Rosenbrock优化算法进行模型参数率定[16];当NSE系数越接近1,径流深相对误差和峰现时刻误差越接近0,说明模拟精度越高。
2 结果与讨论
2.1 流域水文特性
图5给出了沿渡河流域1981-1987年场次洪水降雨量、径流深及径流系数的变化。由图5可以看出,有3场洪水的降水量和径流深超过了200 mm,受降水因素影响,大量级洪水主要集中出现在1982年和1983年,1981年及1984-1987年间发生的洪水量级相对较小。一般而言,径流系数均小于1,然而有接近半数的场次径流系数的计算结果大于1,这并非违背水文过程的客观规律,而是受前期退水影响和洪水场次划分等方面的因素导致的,这一点在本文中并不影响洪水模拟的结果。
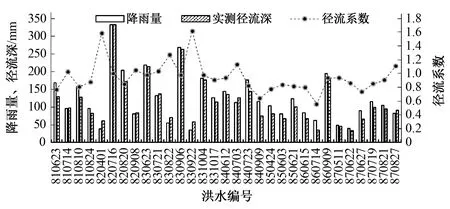
图5 场次洪水降水量、径流深及径流系数图Figu.5 Variation of rainfall, runoff and runoff coefficient at annual and flood-event scales
比较年尺度和场次尺度的径流系数,年尺度和场次尺度的径流系数均值分别为0.79和0.92,可见沿渡河流域属于湿润地区,径流较为丰富。年尺度普遍低于洪水尺度的径流系数,一方面是因为对于年平均径流系数考虑了流域全年在丰平枯水季节的整体规律,而对于洪水径流系数则着重考虑了汛期的变化规律;另一方面如前所述洪水过程的划分受前期退水的影响,使得径流系数偏大。
2.2 各模型应用与评价
对新安江模型、TOPMODEL、BP模型分别进行参数率定。对于新安江模型,先对日模型进行参数率定以满足水量平衡的要求,再率定次洪模型,其中K、WM、B、C、EX、WUM、WLM在次洪模型中通用,其余参数中SM、KI、KG、CS、CG较为敏感,则参考目标函数评价结果在经验取值范围内进行率定。对于TOPMODEL,需要利用ArcGIS计算地形指数再率定,其中土壤下渗率参数m和传导率参数ln(T0)较为敏感,新安江模型和TOPMODEL最终率定结果如表2所示。对于BP模型,选取tansig和logsig为激励函数,采用Levenberg-Marquardt法训练网络,选取训练步数为1 000,误差取10-8,由8-17-1的模型结构可知,共有权值153个,阈值18个,采用自动优选方法进行率定,得出输入层与隐含层、隐含层与输出层之间的连接权值矩阵和隐含层、输出层的阈值矩阵作为模型参数。

表1 新安江次洪模型参数率定结果Tab.1 The calibrated parameters of hourly-based event Xin’anjiang model
根据3种模型的参数率定结果进行洪水模拟,图6给出了以830623号、830906号洪水代表的模拟场次及验证场次的实测洪水过程线与不同模型模拟结果洪水过程线对比图,并统计各模型模拟场次及验证场次的平均径流深、洪峰流量相对误差,峰现时刻误差和NSE效率系数,结果如表3所示。整体来看3种模型均取得了良好的模拟效果,平均径流深误差均底于12%,峰现时刻误差维持在许可误差3 h的范围内,NSE效率系数均大于0.7。就验证期来看,新安江模型模拟结果为三者最优,其径流深平均误差为8.14%,峰现时刻平均误差1.67 h,NSE系数大于0.82,因此模拟精度较高。相对而言,BP模型模拟结果精度较低,各项指标评价值均为3种模型中最低的。

表2 TOPMODEL参数率定结果Tab.2 The calibrated parameters of the TOPMODEL

图6 模拟及验证场次洪水实测与模拟过程Fig.6 Recorded and simulated hydrographs of simulation and validation flood
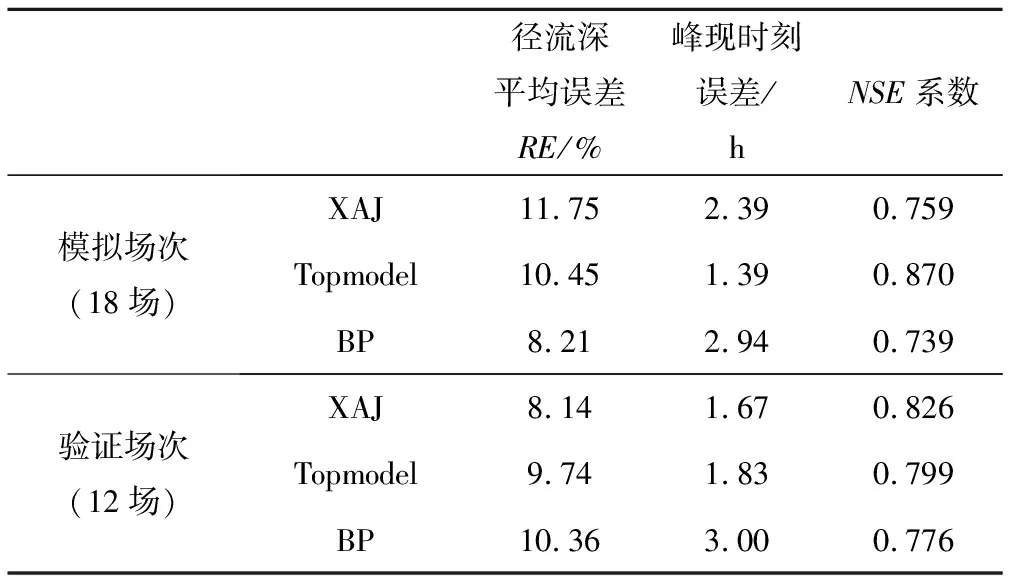
径流深平均误差RE/%峰现时刻误差/hNSE系数模拟场次(18场)XAJ11.752.390.759Topmodel10.451.390.870BP8.212.940.739验证场次(12场)XAJ8.14 1.67 0.826 Topmodel9.74 1.83 0.799 BP10.36 3.00 0.776
为观察分析各场次洪水的模拟情况,绘制12场验证洪水场次的径流深相对误差分布图及NSE效率系数分布图,如图7所示。就径流深相对误差而言,新安江模型的相对误差均在许可误差20%以内,而TOPMODEL和BP模型分别有2场(840703、840909)和1场(831017)相对误差超过20%,其对应的误差值分别为20.34%、-24.65%、-23.63%。因此,从径流深模拟的角度看,新安江模型效果最好,其次是BP模型,最后是Topmodel;就纳什效率系数而言,3种模型验证场次的纳什效率系数均值分别为0.826、0.799、0.776,验证洪水各场次的NSE系数均大于0.6,可见3种模型均达到了精度要求。 并且,NSE系数结果依旧为新安江模拟结果最好,均值达到了0.8以上。
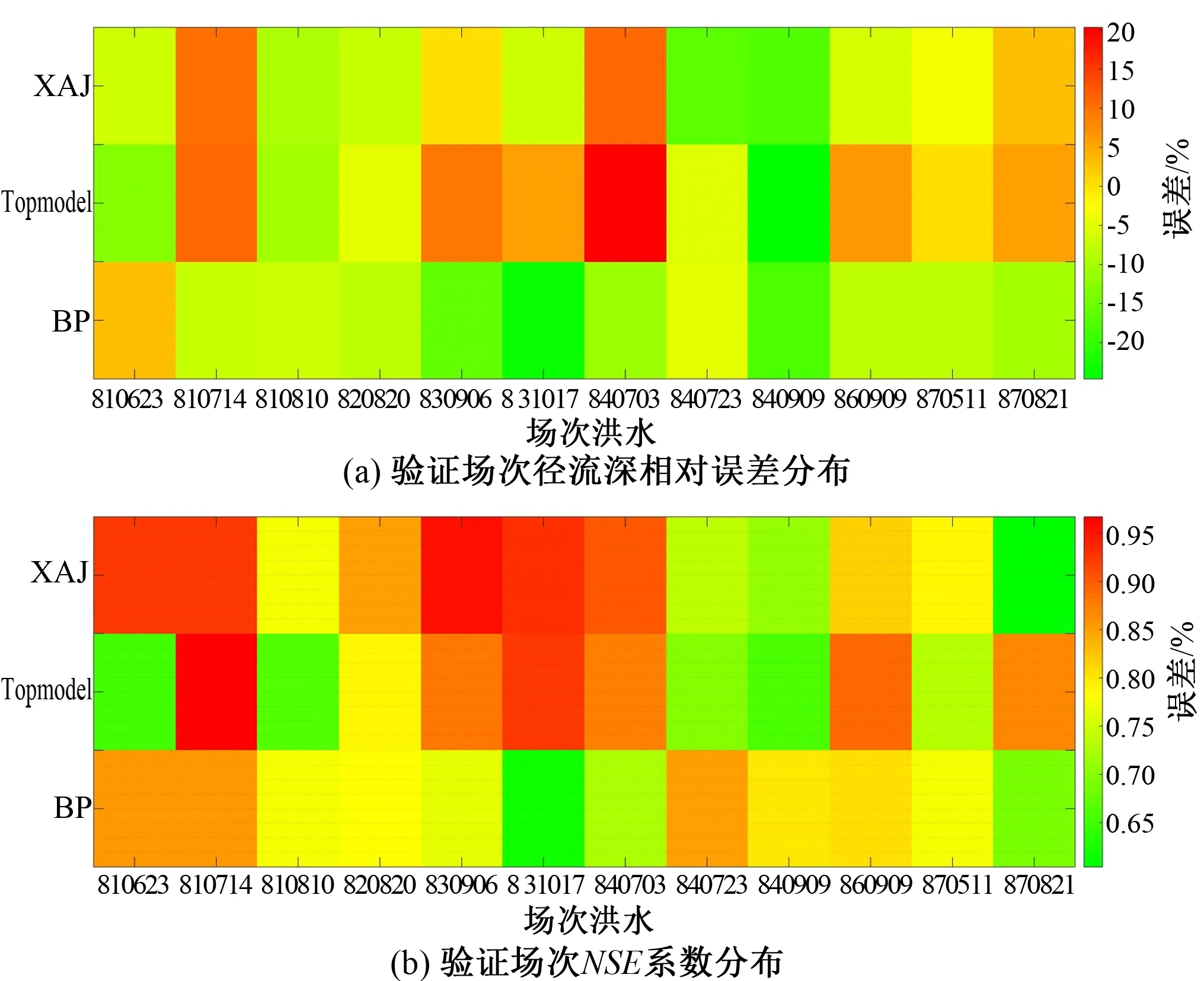
图7 三种水文模型对洪水模拟效果的比较Figure 7 Comparison of relative errors
3种模型实测与模拟流量的散点图如图7所示,可以看出:①新安江模型、TOPMODEL和BP模型在实测与模拟流量之间存在良好的线性关系,其R2值均大于0.8。②BP模型和新安江模型实测与模拟流量点群的相关性分别达到了0.98和0.96,最为接近1∶1线,说明新安江模型和BP模型的模拟结果最接近于真实值,流量模拟效果最好。③TOPMODEL点群较为偏离1∶1线,相关系数为1.11,说明相较而言TOPMODEL在流量过程方面模拟结果相对较差一些,且可以看出其径流模拟值相对实测值普遍偏高。
新安江模型是概念式水文模型,采用蓄满产流计算,适用于湿润地区水文模拟,而本研究区是位于长江上游的湿润地区,新安江模型在此具有良好的适用性,取得了最佳的模拟精度。Topmodel模拟结果相对劣于新安江模型的原因是,参数m的确定与洪量洪峰有较大的关系,30场洪水中,洪水量级差异明显,在率定过程中为保证整体精度率定得出的m,可能使得少数场次洪水的模拟精度不高。BP模型本质上是个黑箱模型,是基于数据驱动的仿真模拟模型,并没有明确的物理成因规律,故其仅在各时刻径流的数值模拟方面结果较好,因此在水量、峰现时刻和NSE系数方面的评价精度远不如洪峰的模拟精度。

图8 3种模型实测与模拟流量比较Fig.8 Comparison of the measured and simulated runoff of three models
3 结 语
(1)沿渡河流域是位于湿润地区的典型中小尺度流域,在次洪模拟的过程中,不同模型在不同评价指标中表现出不同的性能。验证期内新安江模型模拟的平均纳什效率系数最大,径流深相对误差最小,峰现时刻误差最小,取得了较高的精度。而Topmodel和BP模型模拟结果中,均有少数场次的误差超出许可误差要求,前者的水量和流量模拟在三种模型中相对较差;后者的劣势则表现在水量和峰现时刻结果方面。此外,BP模型实测与模拟流量点群与1∶1线最为接近,说明BP模型在流量过程的数值模拟方面效果最好。综合来看,新安江模型在研究区的适用性是最好的,Topmodel和BP模型次之。
(2)不同水文模型对自然现象概化方式不同,导致对于不同评价指标不同洪水场次,各模型的模拟结果之间存在差异,本文应用3种不同类型的模型对沿渡河流域洪水进行模拟,包括新安江模型(概念型集总式水文模型)、TOPMODEL(半分布式水文模型)、人工神经网络模型(数据驱动下的黑箱模型)。这3个模型在各自的模型类别中都具有一定的代表性,将其应用于流域洪水模拟,并进行结果比较,分析各模型的流域适用性,从而为同类地区洪水预报方案的确立提供理论基础和参考依据。

