再析斜面对平抛运动的限制
饶华东 郑睿林
(1. 漳州第一中学,福建 漳州 363000; 2. 漳州第一中学,福建 漳州 363000)
贵刊刊登了李爱华老师的《限制空间范围条件下(类)平抛运动的末速度极值问题举例》一文,[1]文章就平面、竖直面、斜面、抛物面、圆弧面对(类)平抛运动的限制进行了全面、详细的分析,读完该文,深受启发.美中不足的是文中关于斜面对平抛运动的限制的阐述存在一处计算失误和一处表述不当,给笔者阅读该文带来一定的困扰,但瑕不掩瑜,该文不失为一篇极具参考价值的好文章.为避免给更多读者带来困扰,也为了让该文更具完整性、科学性,笔者斗胆指出了文章的错误,并就该文例题3提出了新的解法,同时就斜面对平抛运动的限制进行了拓展分析.
1 原文再现[1]
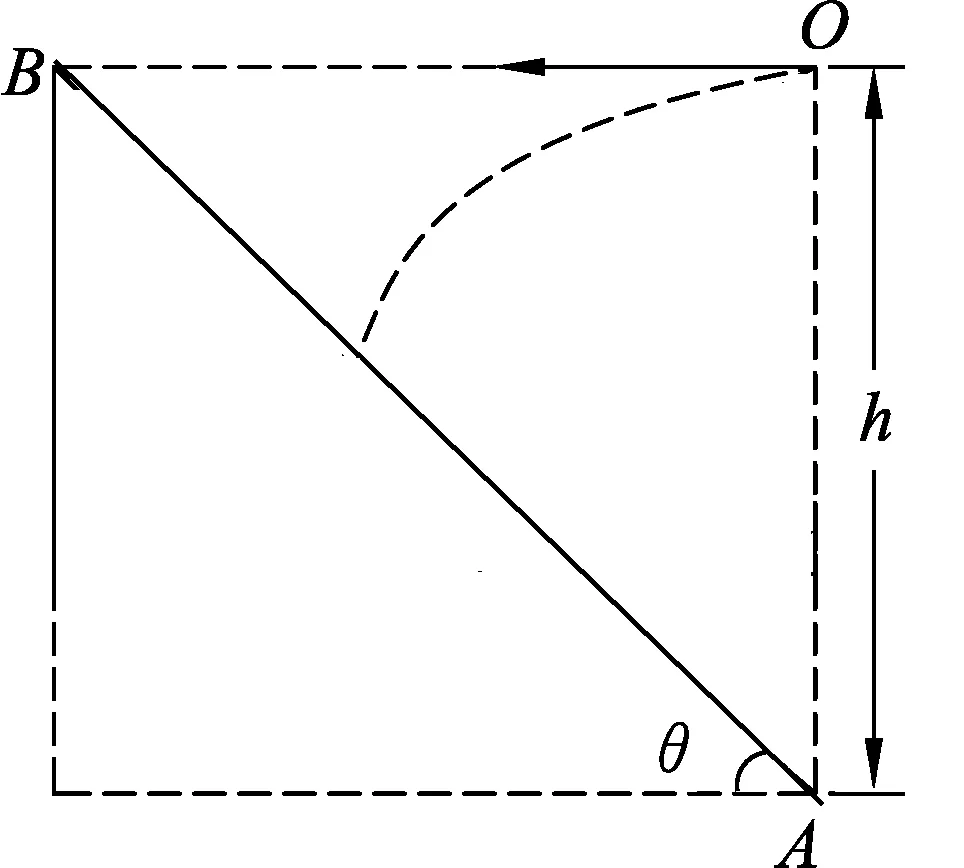
图1 原文图
例1.如图1所示,一质量为m的质点从倾角θ=45°的斜面底端正上方h=2.4 m处水平抛出,不计空气阻力
(B) 若初速度加倍,小球飞行时间减半.
(C) 若小球垂直撞在斜面上,则初速度为4 m/s.
(D) 若落点由A到B逐渐升高,小球落到斜面时的动能逐渐增大.

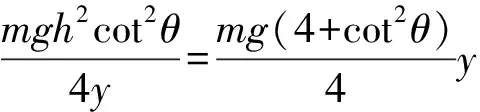
2 错误纠正并提出新解法
2.1 错误纠正
此外,原文题干叙述为“一质量为m的质点”,并未说明是小球,但选项中用“小球”替代了“质点”,显得不够严谨,因为小球不一定能视为质点,两者间不能等同,所以将题干叙述改为“一质量为m的小球(可视为质点)”更为合理.
2.2 利用导数法求解极值
3 拓展与延伸
3.1 抛出点水平右移
例2.例1中,若将抛出点水平右移x距离,试分析x为何值时,落点由A到B逐渐升高,小球落到斜面时的动能一直增大?

图2 抛出点水平右移

3.2 抛出点竖直上移
例3.例1中,若将抛出点竖直上移h′距离,试分析h′为何值时,落点由A到B逐渐升高,小球落到斜面时的动能一直减小?

图3 抛出点竖直上移
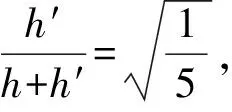
3.3 落点固定,抛出点竖直移动

图4 落点固定,抛出点竖直移动
例4.如图4所示,一质量为m的小球(可视为质点)从倾角θ=45°的固定斜面底端正上方不同位置水平抛出,均落在斜面上的D点,不计空气阻力,已知D、C在同一水平线上,C在A点正上方,x=1 m,试分析h取何值时小球落在D点时的动能最小?
涉及极值求解的题目,要充分利用已知条件,将多变量问题转化为单一变量问题,如本文中小球平抛的初速度、下落高度、空中运动时间等都是变量,根据平抛规律、动能定理及斜面的限制条件,将动能(或末速度)用单一变量(如下落高度)表示,再利用求导或构造均值不等式的数学方法求解.此外,利用函数(如三角函数)的单调性、配方、构造双勾函数等方法也是求解极值的常用方法.这些方法在文献[1]中均有举例,在此不再赘述.

