变分自编码器结合聚类算法在空战态势评估问题上的应用*
杨任农,房育寰,张振兴,左家亮,黄震宇,张 滢
(1. 空军工程大学 空管领航学院, 陕西 西安 710051; 2. 中国人民解放军95939部队, 河北 沧州 061736)
空战态势评估是指在空战环境下根据飞行参数来评估双方对抗态势,是空战决策的前提,在未来智能化空战中起到至关重要的作用。随着越来越多的信息化武器装备部队,战场信息量剧增,如何利用空战数据快速、准确地评估战场态势已成为亟待解决的问题[1]。
空战态势评估方法主要分为两类:非参量法和参量法。其中,非参量法充分考虑了空战态势特征,并使用优势函数定量化分析双方态势信息。高永等[2]考虑到机载武器、雷达搜索等威胁因素,改进了空战态势评估模型;肖冰松等[3]利用战术数据链改进了角度优势函数和距离优势函数;吴文海等[4]提出了基于导弹攻击区的新型优势函数。然而,非参量法中优势函数定义的可移植性差,参数权重的确定主观性强。参量法又称为不确定性理论方法,是利用贝叶斯网络等统计学习方法确定评估指数间的关系。Narayana等[5]利用模糊贝叶斯网络方法建立了空战态势评估辅助决策系统。Azimirad等[6]提出了基于模糊集理论的目标威胁估计算法。然而,当处理较多数据时,参量法存在输入参量少以及特征提取能力不足等问题。此外,参量法和非参量法都忽略了态势变化的连续性。
为了解决上述两种方法存在的问题,本文提出了一种新的无监督态势评估模型。通过分析空战态势要素模型,确定合理的态势特征作为模型输入。考虑到空战态势变化的连续性,提出了基于时间段的态势分析方法。同时,为了避免模型输入维度过高,使用特征提取模型进行数据降维。在没有先验态势信息的情况下,使用聚类算法处理降维后的时间段态势特征,刻画不同态势间的分类关系。
随着大数据时代的到来,深度学习算法为很多复杂问题提供了新的解决思路,尤其是无监督深度学习方法[7]。与有监督学习相比,无监督学习不需要大量有标签训练数据,可以自动学习模型特征。本文选取其典型代表——变分自编码器(Variational AutoEncoder, VAE)作为态势分类的特征提取基本模型。考虑到多层VAE的特征学习能力优于单层VAE,本文使用多层VAE提取态势特征。同时,多层网络的权值训练问题一直是个难题,本文使用不确定性权重限制玻尔兹曼机(Weighted uncertainty Restricted Boltzmann Machines, WRBM)[8]预训练VAE的权重值, Adam优化器[9]训练网络。同时引入混合密度网络(Mixed Density Network, MDN)[10-11]对输出概率分布加权求和,提高模型的非线性拟合能力和数据生成能力。
在实验部分,主成分分析法(Principal Component Analysis, PCA)、VAE、VAE-WRBM和VAE-WRBM-MDN四种特征提取算法分别与K-means++和密度峰值两种聚类算法构成50个横向纵向对比实验,实验结果表明算法可靠性较高,具有实际应用价值。
1 空战态势模型构建
1.1 空战态势描述
1.1.1 评估参数
在1V1空战中,态势评估的主要任务是根据飞机位置、角度和机动状态确定敌我当前态势。对抗双方的几何位置关系如图1所示,在机体坐标系OXYZ中,选取飞机的重心为坐标原点O,X轴沿飞机纵轴,指向机体正前方;Y轴垂直于战机对称面,指向右方;Z轴位于战机对称面并垂直于机体纵轴,指向下方;方位角λ表示目标视线与我机速度方向之间的夹角;ε表示目标视线延长线与目标机速度方向之间的夹角;Vw表示我机速度矢量;Vt表示目标机速度矢量。

图1 空战双方位置关系Fig.1 Position relationship between two sides in air combat
在空战行动中,双方都试图尽快占据有利位置并采取合适的速度,力求先敌瞄准,先敌发射,先敌命中。因此,在描述空战态势时,对抗双方的距离、速度和角度等参数具有重要意义。结合空战机动仪表提供的实际空战数据和图1显示的空战双方相对参量,确定一组空战态势参量,如表1所示。

表1 空战态势参数
1.1.2 特征维数
考虑到空战态势变化具有连续性,不能仅仅根据某一时刻的态势值衡量机动动作对态势的影响。本文选取时间段数据作为态势评估对象,构建了基于连续数据序列的态势评估模型。根据专家经验,将时间段长度设置为25。由于每组空战态势参量包含8个特征数据,将每个时间段的特征数据按时间顺序排列,可以得到维数为200的时间段特征数据。
1.2 态势空间分类
美国国防部联合指挥实验室(Joint Direction of Laboratories, JDL)将空战态势定义为信息融合的第二级融合。其将一级融合获取的数据进行分析,从而对战场情况进行评价,为后级融合奠定基础,同时为飞行员提供决策参考[12]。本文根据连续时间段数据信息将空战态势按照经典分类方法分为四类:我方占优V1,敌方占优V2,双方中立V3和双方均势V4,如图2所示。
(a) V1

(b) V2
(c) V3

(d) V4图2 四类经典空战态势Fig.2 Four kinds of classic air combat situations
在图2中,由敌我机位置关系可以看出:V1表示我机占据优势位置,目标方位角小,目标进入角小,双机距离小,我机具有更高速度和高度,并且达到攻击条件;V2表示敌机占据优势位置,目标方位角大,目标进入角大,双机距离小,敌机具有更高速度和高度,达到攻击条件;V3表示双机中立,双击距离大,目标进入角小,双方均不具备攻击优势;V4表示双方力量均势,双方距离小,目标方位角小,目标进入角大,双方速度和高度基本一致,均达到攻击条件。
2 特征提取
飞行数据序列由长度为L的时间序列X={x(1),x(2),…,x(L)},x(i)∈R200表示。为了避免维数灾难,提高态势分类的准确性,使用一种新的无监督深度学习模型VAE-WRBM-MDN提取空战态势数据中的关键特征。
2.1 数据处理
战机运行环境的多变性以及吊舱数据接收的不稳定性和误差性,使得飞行数据具有坏值和噪声。因此,在进行态势分类之前,需要对数据进行清洗。数据清洗的主要步骤如下:
1)剔除异常值。孤立森林算法是一种基于非参量法和无监督学习的异常值检测算法[13],能够快速准确地处理大量数据,尤其适用于大数据环境。并且孤立森林算法的性能优于交互避碰(Optical Reciprocal Collision Avoidance, ORCA)算法[13]、局部异常因子(Local Outlier Factor, LOF)算法[14]和随机森林(Random Forest, RF)[15]算法。因此,选取孤立森林算法检测飞行数据中的异常值。
2)坐标系转换。为了定量分析战机间的相对态势,将GPS获得的WGS-84大地坐标系转化为我国国家坐标系。
3)归一化处理。考虑到使用深度学习方法处理取值范围较大的数据会出现收敛速度慢、训练时间长等问题,为了保持数据范围的统一性,对数据进行归一化处理,即:
(1)
2.2 基于双向LSTM的VAE模型
变分自编码器是一种无监督生成模型[16],由生成模型和推理模型组成,能够更加准确地提取高维非线性数据的重要特征,可以进行特征提取、数据生成、高维数据可视化和异常值检测等[17]。VAE具有典型的变分推理框架,在给定可视变量x条件下,可以用来学习低维隐含变量z。与标准的自动编码器相比,VAE中的x和z都是随机变量,VAE的输出值是它们的参数分布值,VAE的权值代表变分参量φ和θ。
VAE能够求得给定可视变量x的条件下编码器(encoding model)的概率分布qφ(z|x),隐含变量条件的前向分布p(z)以及给定隐含变量条件下解码器(decoding model)的概率分布pθ(x|z)。其中,qφ(z|x)估计出真实的未知后向分布p(z|x),实现了生成模型。
双向长短期记忆网络(Bidirectional Long Short-Term Memory, BLSTM)[18]可以同时获得前向和后向信息,适合处理时间序列数据。与LSTM相比,BLSTM具有更高的时间序列预测精度和速度。因此,使用BLSTM作为构成编码器和解码器的基本网络模型。同时,为了提升网络的学习能力,堆叠多层BLSTM构建深层BLSTM网络。单层BLSTM的前向序列、后向序列和输出为:
(2)
式中,g(·)表示激励函数,Wmn表示从第m个神经元到第n个神经元的权值,bn表示第n层的偏移量。
对于可视变量和相对应的隐藏变量,假设存在因式分解:
p(x1:T,z1:T)=
(3)
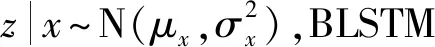
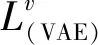
(4)

为了进一步提升VAE的性能,从优化初始权重和提高生成数据的相似性两个方面进行优化。
2.3 WRBM优化初始权重
对于具有多层隐含层的VAE,初始权重的优化十分重要。若初始权重值过大,VAE将会陷入局部最小值;若初始权重值过小,则前几层的梯度变化会很小,无法训练权值。因此,为了获得最优权重值,引入WRBM网络来学习隐含层特征,将训练好的权重值作为VAE的初始权重。其中,WRBM在RBM的基础上,将权重随机变量引入到传统后向传播算法中,有效地避免了神经网络的过拟合。
为了保证WRBM的权重和VAE权重相对应,WRBM的数目以及WRBM包含的神经元数目要与VAE的层数和每层隐含单元的数目相一致。使用前一个WRBM学习完单层VAE的权值后,WRBM的输出将作为后一个WRBM的输入。
2.4 MDN-VAE模型
MDN通过对网络输出层概率的分布函数进行加权求和,得到每个输出值的概率。与MDN相比,VAE模型直接输出分布参数,没有考虑到不同输出值的权重,不符合实际生成数据的特点。因此,为了改善网络提取特征的能力和生成数据的相似性,将MDN引入到VAE模型中。
对于输出层,选取高斯函数作为概率密度函数(Probability Density Function, PDF),其定义为:
(5)

N(·)中的参数按照如下方法进行标准化:
(6)

(7)
改进VAE的结构和流程图如图3和图4所示。
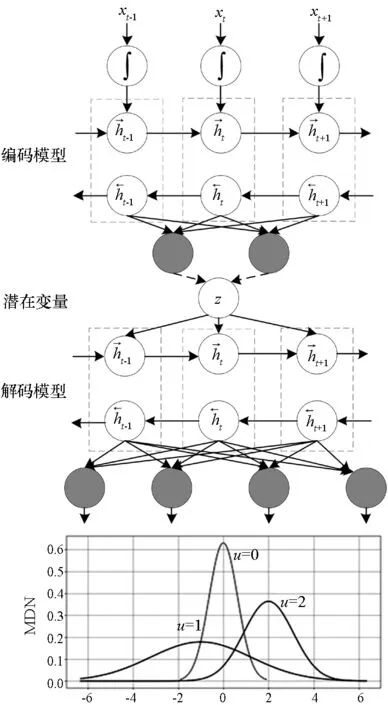
图3 MDN-VAE模型结构图Fig.3 Structure figure of MDN-VAE model
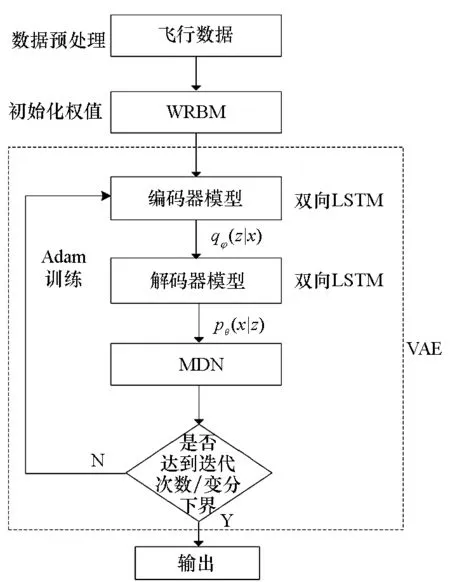
图4 MDN-VAE模型流程图Fig.4 Flow chart of MDN-VAE model
3 K-means++和密度峰值聚类算法
由1.2节可知,四种典型的空战态势特征值具有很明显的差别,并且同一类态势相关的特征会聚集在一起。因此,引入两种典型聚类算法——K-means++和密度峰值算法对提取的空战态势特征进行分类。
3.1 K-means++
K-means++[19]由Arthur和Vassilvitskii于2007年提出,相比于K-means,它使用新的算法来代替随机选取聚类中心的方法,改进了聚类中心的确定方法,有更高的准确度和收敛速度。具体计算步骤见文献[19]。
3.2 密度峰值算法
密度峰值算法[20]主要根据数据点i的两个重要特征进行分类:局部密度值ρi和点i与其更高密度点间的最小距离δi,具体表达式如下:
(8)
式中,dc表示截断距离,ρi表示距离点i小于dc的点的数量。δi反映了高密度点间的距离:
(9)
由于聚类中心点周围应该分布着低密度点,并且与其他聚类中心保持一定距离。因此,数据点可以看作是聚类中心点的充要条件是ρi和δi均高于某一阈值。
4 优势函数的建立
为了提高态势分类的准确度,使得态势分类与真实战场态势相对应,使用优势函数以及战场情况修正分类结果。计算优势函数值时,以所取时刻点为中心,根据与所取时刻点的距离,向前向后各取12个点,时刻点距所取时刻点越近,其权重值越大。
在态势评估中,战机的空战能力和战场态势是两个主要因素。其中,空战能力的优势函数Tc[4]为:
Tc=C/max(C)
(10)
C=[lnB+ln(∑A1+1)+ln(∑A2)]ε1ε2ε3ε4
(11)
式中,C是空战能力,B是机动参数,A1是火力参数,A2是探测参数,ε1是操纵系数,ε2是生存系数,ε3是导航系数,ε4是电子对抗系数。
战场态势主要考虑角度优势函数Ta、距离优势函数Td、速度优势函数Tv和高度优势函数Th,具体表达式见文献[4]。空战态势优势函数T为:
(12)
式中,k1,k2,k3,k4,k5分别表示空战能力优势、角度优势、距离优势、速度优势和高度优势权重。使用模糊层次分析法计算每个优势函数的权重系数,解得k1=0.32,k2=0.19,k3=0.15,k4=0.13,k5=0.21。
具体的空战态势评估数据的存储形式如图5所示。

图5 数据存储形式Fig.5 Storage format of data
在图5中,态势参数由25组连续的态势参数组成,每组态势参数包含8个参数(见表1);态势分类采取[0 0 0 1]的形式,1的位置表示态势分类情况;态势值根据上述方法进行计算。
态势分类整体流程图如图6所示。
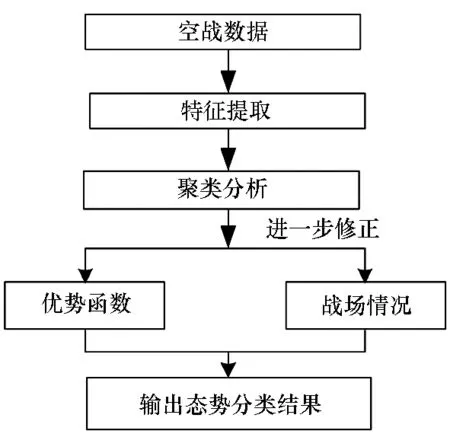
图6 态势分类流程图Fig.6 Flow chart of situation classification
5 实验仿真
实验仿真的硬件环境为具有12 Intel Xeon(R) E5 CPU和4GB RAM的高性能处理器,软件平台为Google公司最新研发的Tensorflow深度学习算法库。实验数据是空战对抗演习数据,通过飞机传感器得到,共有50组,每组包含50 000个训练数据和5000个测试数据。
5.1 特征提取实验
使用BLSTM模型构建一个四层VAE网络,为了获取更优的训练参数并进一步提升网络性能,通过改变输出层神经元数目、学习率和batchsize等参数,进行了多组实验。不同参数下的VAE-WRBM-MDN训练过程如图7~9所示。

图7 不同输出训练过程Fig.7 Training process of different outputs

图8 不同学习率的训练过程Fig.8 Training process of different learning rates
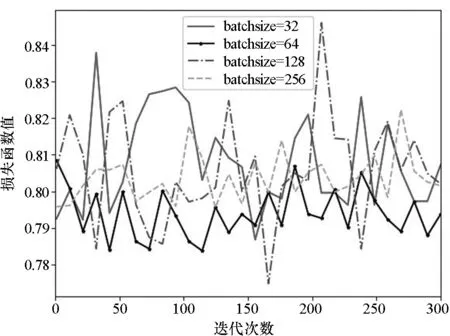
图9 不同batchsize的训练过程Fig.9 Training process of different batchsizes
由图7~9可知,VAE-WRBM-MDN的结构为[1024 256 64 2]时(表示VAE网络共包含四层BLSTM网络,每层网络神经元的数目分别为1024、256、64和2),Adam优化器学习率为0.005,batchsize为64时,能够获得较低的训练误差,具有较好的鲁棒性。
根据上述方法,得到了不同网络的最优参数:①WRBM的学习率为0.001,batchsize为64,dropout为0.6,迭代次数为500;②VAE的学习率为0.005,batchsize为64,dropout为0.6,迭代次数为300;③VAE-MDN的学习率为0.005,batchsize为64,dropout为0.6,迭代次数为300。
结构为[200 1024](WRBM输入层和输出层神经元数目分别为200和1024)、[1024 256]、[256 64]、[64 2]、[2 64]和[2 64]、[64 256]、[256 1024]、[1024 200]的WRBM的训练过程如图10所示。
由图10可知,WRBM经过100次左右的迭代已经收敛到较好的精度,具有良好的收敛速度和精度。因此,WRBM可以很好地建立输入和输出间的映射,为VAE模型提供了良好的初始权重值。
VAE-WRBM和VAE-WRBM-MDN的训练过程如图11所示。
由图11可知,VAE-WRBM和VAE-WRBM-MDN经过150次左右迭代,可以收敛到一个相对稳定的范围,具有较好的全局搜索能力和鲁棒性。而在VAE的训练过程中,其损失值一直保持无穷大。通过分析,是由随机的初始权值和复杂的训练数据造成的。因此,对于VAE模型,利用WRBM优化权值是十分必要的。

(a) Encode 1 (b) Encode 2 (c) Encode 3

(d) Encode 4 (e) Decode 1 (f) Decode 2

(g) Decode 3 (h) Decode 4图10 WRBM的训练过程Fig.10 Training process of WRBM

(a) VAE-WRBM训练过程(a) Training process of VAE-WRAM

(b) VAE-WRBM-MDN训练过程(b) Training process of VAE-WRBM-MDN图11 VAE-WRBM和VAE-WRBM-MDN的训练过程Fig.11 Training process of VAE-WRBM and VAE-WRBM-MDN
5.2 分类实验
将提取的特征输入到K-means++和密度峰值法分类器中,并以一组测试数据为例,将分类结果可视化。密度峰值算法数据点分布如图12所示。

图12 密度峰值算法Fig.12 Value of density peaks algorithm
在图12中,组1、组2、组3、组4四个实心点分别代表了四类态势的中心。依据第4节优势函数的建立方法,将优势函数值和真实战场情况与分类结果相对应,得到的匹配结果为:组1代表态势V3,组2代表态势V2,组3代表态势V4,组4代表态势V1。从中心点出发,以一定距离作为分类半径将剩余的点归类。如果存在重叠区域,则根据与中心点的距离进行分类。分类结果如图13所示。

图13 密度峰值算法聚类结果Fig.13 Cluster for density peaks algorithm
在图13中,横轴代表聚类实验中的5000个测试数据,纵轴代表四类态势。显然,分类结果中存在很多离散点,不符合空战态势连续变化的特点,需要进一步修正。
K-means++算法数据点分布如图14所示。
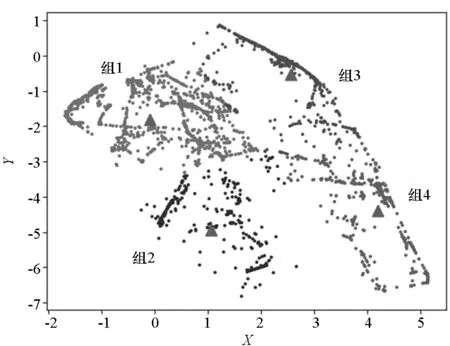
图14 K-means++算法Fig.14 Value of K-means++ algorithm
在图14中,由散点的颜色深浅和分布规律可以大致看出所有散点分为四组,四组散点中的三角形代表四个聚类中心。与密度分类法同理将四分类组与态势对应。组1对应V3,组2对应V2,组3对应V4,组4对应V1。具体的分类结果如图15所示。
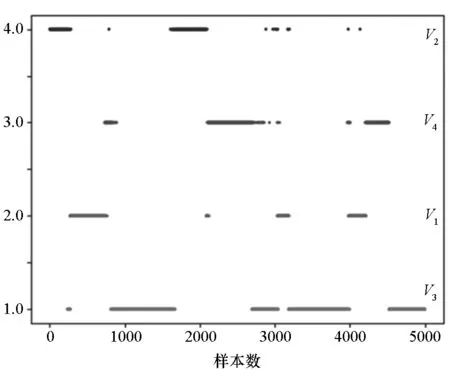
图15 K-means++算法聚类结果Fig.15 Cluster for K-means++ algorithm
与图13类似,图15的分类结果中仍有部分离散点处于分类边缘,不符合空战规律,需要根据优势值和战场情况进行修正。由于分类结果存在一些离散点,需要结合优势函数和战场情况进行改进。以部分态势数据为例说明如何利用优势函数和战场情况进行改进的。其中,部分态势数据的优势函数值和聚类结果如图16所示。
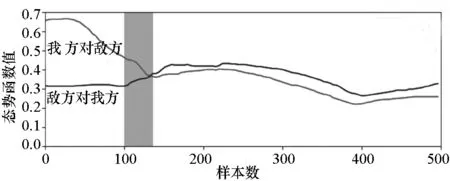
(a) 双方优势函数值曲线(a) Curve of dominant function value of both sides
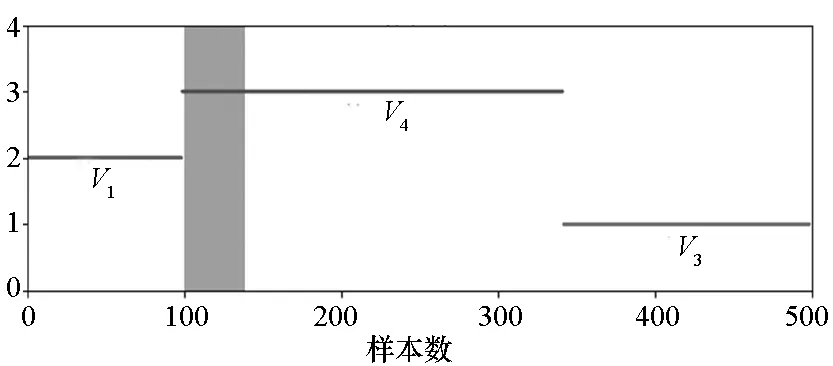
(b) 聚类算法分类结果图(b) Graph of clustering algorithm classification图16 两种聚类算法对比Fig.16 Comparison of two algorithms

图17 分类结果Fig.17 Classification results
在图16中,阴影区域内的优势函数表示我方具有优势,但聚类结果却显示双方均不适宜攻击,不符合实战态势,需要进行修正。差异均处于态势变化的临界状态附近,说明这些时刻数据变化具有连续性。由此可知,空战态势变化是连续的过程,态势评估的目标应该选择时间段数据。因此,图13和图15的分类结果需要参考优势函数和战场情况,力求提升分类结果准确度。最终结果如图17所示。
为了测试算法的特征提取能力和分类准确度,使用PCA方法进行对比实验。按照上述步骤,共进行了50组对比实验。实验结果如表2所示。

表2 分类效果对比表
由表2可知:
1)直接使用K-means++或者密度峰值进行态势分类得到的准确度较低,无法实施态势评估或制作标准样本库。说明典型的聚类算法不适用于高维的特征数据。
2)对于测试集和训练集,与PCA算法相比,VAE-WRBM和VAE-WRBM-MDN两种改进VAE特征提取模型均取得了较好的结果,并且VAE-WRBM-MDN较VAE-WRBM性能更优。说明PCA主要针对线性数据,并且不适用于多维复杂非线性数据。
3)针对特征模型提取后的数据,K-means++和密度峰值两种典型的聚类算法均得到了较准确的分类结果,并且密度峰值算法稍优于K-means++。这说明提取的特征可以代表输入的时间段态势特征,并且典型的聚类方法也很有效。
4)就单组数据运行时间而言,通过表格中的数据对比,可以看出改进的VAE模型+分类算法的运行时间稍长于PCA+分类算法的运行时间,但是准确率却明显高于后者并且运行时间均低于0.5 s,符合实际应用标准。综合来看,本文提出的VAE-WRBM-MDN态势分类方法性能更优。此外,算法对硬件要求较低,具有实用性。
利用训练好的VAE-WRBM-MDN网络模型和密度峰值算法处理实际空战数据,对每个时段的空战态势进行分类,并结合实际飞行状况进行对比分析,具体的输出结果如图18~20所示。
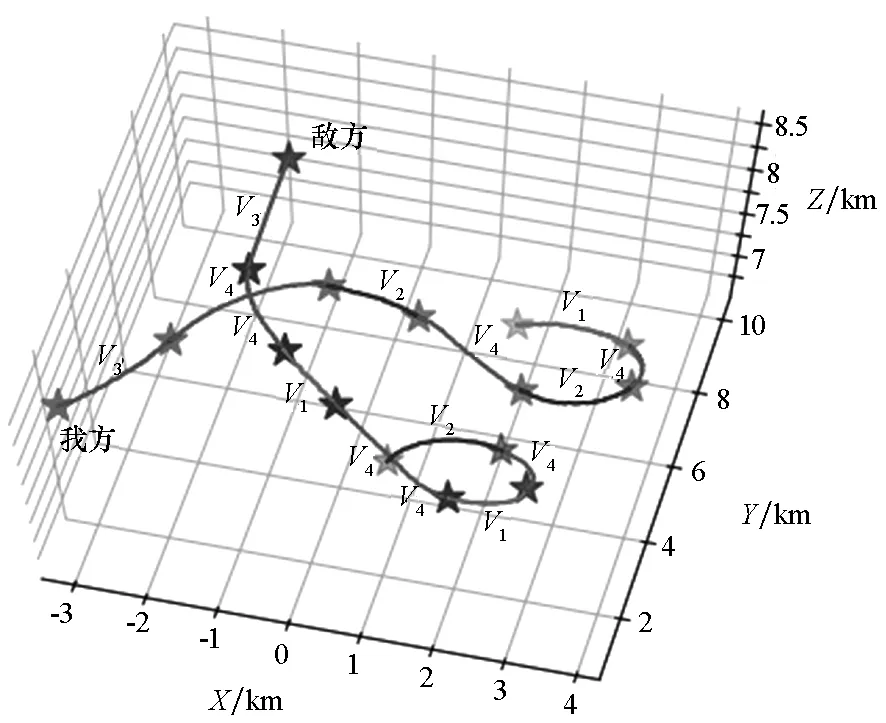
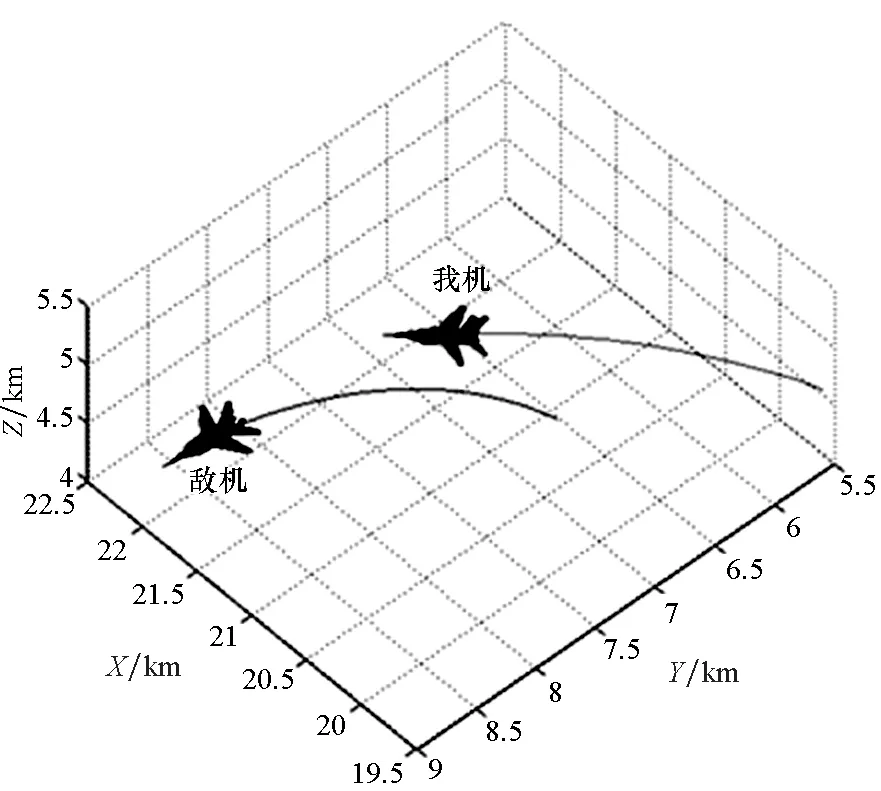
图18 1V1空战实例三维态Fig.18 Three-dimensional situation of 1V1 in air combat

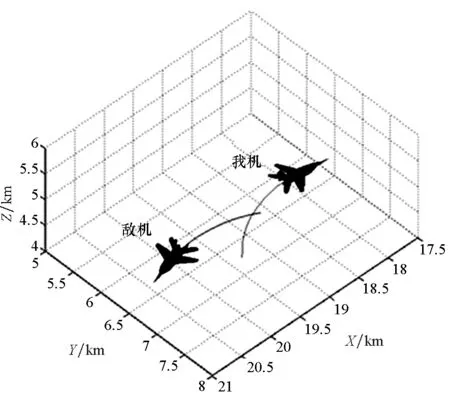
图19 1V1空战实例二维态势Fig.19 Two-dimensional of 1V1 in air combat

图20 空战态势值Fig.20 Situation value of air combat
图18和图19显示了二维和三维的实时态势分类结果,图20显示了态势值和对应的分类结果。根据态势,使用V1~V4标记航迹。模型将实例中的对抗过程分成7部分。Part 1对应态势V3:在进入阶段,两机距离大,均达不到攻击条件。Part 2对应态势V4:双方均开始做机动并进入对抗区域,互相构成威胁。Part 3对应态势V2:敌方出现在我方侧后方,我方处于劣势。Part 4对应态势V4:尽管敌方在角度上具有些微优势,但是我方在高度上占优,双方处于均势。Part 5对应态势V2:敌方实施较大机动,扩大了其在角度上的优势同时缩小了两机高度差。因此,我方处于劣势。Part 6对应态势V4:双方均进行机动企图攻击对方。Part 7对应态势V1:经历了Part 5和Part 6,我方占据角度和高度优势,形成尾后击敌优势。模型判断我方占优。图20所示态势变化规律基本与图18和图19所示分类结果一致。
通过分析对抗过程,可以得出模型的输出结果与真实态势一致,验证了模型的有效性。
6 结论
本文结合改进的VAE、聚类算法、优势函数和战场情况,提出的空战态势评估算法具有良好的可移植性并克服了传统方法在线计算优势函数的局限,为解决空战态势评估提供了新视角。通过丰富空战态势样本库,可以实现多种机型,多种作战模式下的态势评估。
主要创新点如下:①优势函数和无监督深度学习聚类算法的结合提升了态势评估的准确度;②WRBM优化了VAE的初始权值,缩短了算法训练时间,同时避免结果陷入局部最优值;③MDN提升了网络提取特征和生成数据的能力。
本文为后续研究提供许多想法:①后续可以尝试其他无监督分类算法,比如生成对抗网络等,进一步提升准确性;②本文提出的方法可以实时评估,也可以产生标准的态势评估样本库,为深度置信网络等有监督深度学习提供训练数据;③VAE-WRBM-MDN具有很强的生成新数据的能力,后续可以进行数据生成实验;④结合相关要素,细化分类类别,提高态势分类参考价值。

