基于单位约束组合赋权的混凝土坝性态安全评价云模型

(南昌大学 建筑工程学院，南昌 330031)

1 研究背景

混凝土坝复杂的结构和工作条件导致影响其工作性态的因素众多，因此对混凝土坝的运行性态进行安全评价存在着许多不确定性，特别是模糊性和随机性。目前常用的一些评价方法在评价指标权重的确定上缺乏可靠性和科学性，权重的确定成为安全评价过程中的一个难点。安全评价中常用的赋权方法有主观赋权法[1-2]和客观赋权法[3-4]，但都各自存在着不足。主观赋权法太过于依赖专家的主观经验，主观的随意性太强，赋权结果容易受专家专业程度的影响；客观赋权法根据实际数据确定权重，但是这类方法太过于依赖实际问题，人的参与性和通用性较差，有时甚至会出现确定权重和实际情况相悖的结果。

针对单一使用主观或客观赋权法所存在的不足，人们又提出了新的赋权方法——组合赋权法。该类方法结合了主、客观赋权各自的优点，既考虑了实际的数据又参考了专家的意见，使指标的赋权实现了主观与客观的统一，在某些领域得到了较好的应用[5-7]。近些年来，关于运用组合赋权方法对影响大坝性态安全的评价指标进行赋权的研究也取得了一些进展，如张瀚等[8]利用多效应量获取大坝健康指标的隶属度，并结合信息熵理论和专家评估法的组合赋权方法确定大坝健康指标的权重，从而实现了对大坝分部位动态健康评价；张帅等[9]通过采用层次分析法与信息熵结合的组合赋权方法确定了大坝性态安全指标权重，并通过建立大坝性态安全模糊综合评价模型实现了对老园水库大坝性态安全的综合评价。但上述方法对于组合赋权中主、客观权重系数的分配通常都是人为主观确定的，缺乏一定的理论依据，且在各评价指标隶属度确定过程中对于模糊性和随机性的考虑也有所欠缺。

本文提出应用基于单位约束条件下最优组合赋权方法[10]对评价指标进行赋权，该方法不再以权向量为基础进行组合，而是以评价值向量作为组合基础，通过在单位约束条件下对基于G1法与熵权法的主客观赋权方法进行寻优组合，确定出最优的组合权重，使得评价指标权重的确定更加科学和全面；同时，考虑到评价过程中隶属度区间的模糊性[11]，引入云模型理论，建立基于单位约束的组合赋权评价云模型，并把它应用到混凝土大坝性态安全评价当中，以期对大坝进行更加全面和准确的安全评价。

2 混凝土坝性态安全评价指标体系及标准

混凝土坝性态安全评价是一个多因素、多层次的复杂系统工程，影响大坝健康的因素众多。本文综合考虑各个因素，参考混凝土坝安全规范[12]和有关文献[13-14]，并结合所收集的观测资料，从大坝的变形、渗流、应力3个方面建立了混凝土坝性态安全评价指标体系，见图1。考虑到已有的等级划分方法[13-14]和相应规范[12]将混凝土坝性态安全评价指标划分为5级，得到评语集(I，II，III，IV，V)=(安全，较安全，中等安全，较不安全，不安全)与其对应的评价区间{[1,0.8], (0.8,0.6],(0.6,0.4],(0.4,0.2], (0.2,0]}。

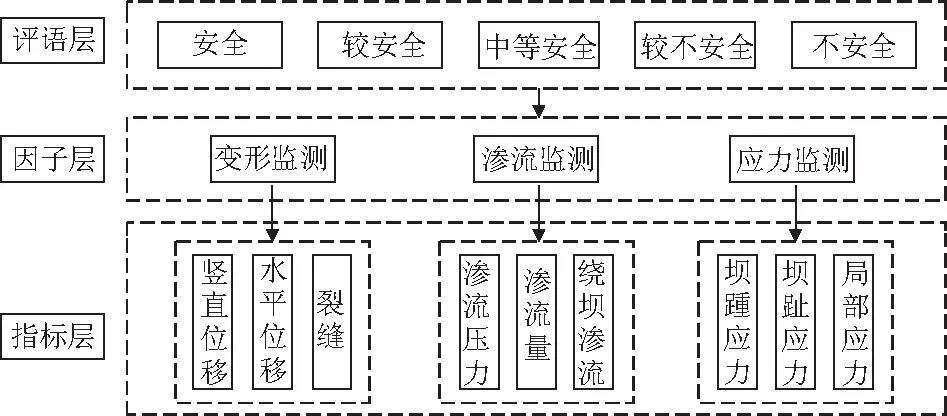
图1 混凝土坝性态安全评价指标体系Fig.1 System of evaluation indicators of concretedam performance

3 融合单位约束组合赋权与云模型的混凝土坝性态安全评价模型

3.1 梯级逐层指标组合赋权方法

3.1.1 主观权重的确定

层次分析法(AHP)[15]是主观赋权中较为常见的一种方法，它将一个复杂系统中各种影响因素按层次进行有序的划分，条理清晰明确，在多目标、多准则的系统评价中应用比较广泛。但AHP中计算权重大多使用的是特征值法，用该方法计算权重，判断矩阵中每两两元素之间需进行比较，当比较的元素较多时，计算量大而且繁琐，很难达到一致。因此本文采用了G1法[16]进行主观权重的计算，该方法与AHP法相比无需构造判断矩阵，也不用进行一致性的检验，计算量较少，方便简洁。

具体的原理及计算步骤如下：

(1)由专家确定指标间的一组由大到小的排序关系。

(2)专家对相邻的指标Xk-1与Xk之间重要性的程度作一个理性的赋值。

(3)假设rk表示相邻指标Xk-1和Xk之间重要程度的比值，即

rk=Wk-1/Wk,k=n,n-1,…,3,2 。

(1)

式中：Wk为第k个指标的权重；rk先由各个专家独自判定，然后取其平均值，rk的取值参考文献[17]；n为指标个数。

(4)专家给出rk的理性赋值后，主观权重pj计算式为

(2)

Wk-1=rkWk,k=n,n-1,…,3,2 。

(3)

3.1.2 客观权重的确定

熵值可以体现信息无序化的程度，表现出指标所含信息量的大小[18]。指标所包含的信息量越多，它的有序程度就越低，熵值就越小，权重就越大。用熵权法计算，结果客观、严谨，所以本文采用熵权法确定指标的客观权重。具体计算步骤如下：

(1)假设大坝安全评价指标样本数目为m，指标个数为n，且xij表示第i个样本的第j个指标的属性值，则判断矩阵X为

X=[xij]m× n,

i=1,2,…,m;j=1,2,…,n。

(4)

(2)对判断矩阵中的数据进行归一化处理，对越大越好的指标，令

(5)

对越小越好的指标，令

(6)

式中xmaxj,xminj分别表示在第j个指标下各监测样本中的最大值和最小值。

(3)确定评价指标的熵值，即

(7)

式中fij为基于指标j的样本i所占的比重。

(4)用熵值计算各指标的客观权重，即

(8)

3.1.3 基于单位约束的组合赋权

本文在单位约束函数条件下对评价指标进行优化组合赋权，此方法不再只以权向量为基础进行组合，而是以最终评价结果向量为组合基础，对建立的不同优化模型中的线性组合向量W进行系数求解。具体过程如下：

(1)求评价指标权重Wj，即

Wj=x1pj+x2qj,j=1,2,…,n，

(9)

x12+x22=1 ,x1,x2≥0 。

(10)

式中：Wj表示评价指标的权重；pj是G1法确定的主观权重；qj是熵权法确定的客观权重；x1,x2为组合赋权系数向量的线性相关系数；x12+x22=1为单位化的约束条件。

(2)最优组合赋权的问题关键就在于确定x1,x2的值，根据线性加权法，第i个对象的指标评价值可表示为

(11)

式中bij为第i个对象对于第j个指标的属性值。

(3)多指标组合赋权的系数向量W的确定原则在于使Di尽可能分散，以便更好地体现出各评价指标之间的差异，所以对组合赋权的寻优问题可以转化成下列问题的求解，即

(12)

(4)构造Lagrange函数求解x1,x2，设

(13)

令∂L/∂x1,∂L/∂x2=0,且λ是Lagrange乘子，即

(14)

(5)联立式(9)—式(14)求解x1,x2，并对结果进行归一化处理，则优化系数x1′,x2′为

(6)求解最优组合模型的组合权重，具体计算式为

(16)

(7)最终各评价指标的组合权向量为W=[W1,W2,...,Wn]。

3.2 混凝土坝性态安全评价云模型

云模型是由李德毅院士提出的一种利用语言值来实现定性与定量之间相互转换的模型，如今在数据挖掘、安全评价等领域得到广泛的应用。事物的模糊性与随机性在云模型中通过期望(Ex)、熵(En)、超熵(He)3个特征参数进行有机的结合，从而实现了定性概念和定量数据间不确定性的相互转换。设U是精确数值表示的一个定量论域，C是U上的定性概念，对于区间U上的一个随机数字x，其对C的确定度u(x)∈[0,1]是具有稳定倾向的随机数，则我们称x在U上分布为云分布。

若x满足：x～N(Ex,(En′)2)，En′～N(En,He2)，且x对C的确定度可以表示为

ux=exp[-(x-Ex)2/((En′)2) 。

(17)

则x在U上的分布为正态云，正态云模型是云模型中最基本、最重要、应用最广泛的云模型。在正态云模型中，特征参数Ex是该论域区间的中心值，也是最能代表定性概念的值；En表示该定性概念在论域区间能被接受的范围，是定性概念的模糊度量；He是熵的熵，反映了云滴的离散程度。

混凝土坝性态安全评价过程中定性概念与定量数据间的相互转换可以通过MatLab软件，运用正态云模型发生器来实现，具体过程如下：

(1)步骤 1，生成以期望为Ex、标准差为He的正态随机数En′。

(2)步骤 2，生成以期望为Ex、标准差为En′的正态随机数xt。

(3)步骤 3，由步骤1和步骤2求解确定度，公式为

ut=exp[-(xt-Ex)2/2(En′)2] 。

(18)

(4)步骤 4，重复步骤1到步骤3，直到得到足够多的云滴为止。

特征参数Ex可通过评价指标的标准区间进行确定，即

(19)

由于各评价区间的边界值是2个评价级别之间的过渡值，相对来说是比较模糊的一个边界，它对2个区间的隶属度应该相等，即

(20)

由式(20)得：

(21)

He=K。

(22)

式中K为经验值，可根据实际情况进行调整。

结合式(18)将评价指标的实测值xt运用正态云发生器计算出各评价指标的确定度，即为各评价指标对于各等级区间的隶属度。Rjl表示第j个评价指标对于第l个安全等级的隶属度，则可得隶属度矩阵R为

j=1,2,…,n，l=1,2,…,5 。

(23)

在此之前，要对实测数据进行归一化处理。

3.3 混凝土坝性态安全评价流程

由式(16)求得的组合权重向量W与式(23)得到的隶属度矩阵R计算出混凝土坝性态安全评价的模糊评价矩阵Z为

Z=W×R。

(24)

根据最大隶属度原则[19]作出最终的评价结果，具体步骤见图2。

图2 混凝土坝性态安全评价模型流程Fig.2 Flow chart of safety evaluation model forconcrete dam

4 工程实例

4.1 工程资料

某Ⅰ等水利枢纽工程主要由混凝土重力坝、坝顶开敞式溢洪道、泄水底孔及发电厂房等主要建筑物组成，为确保大坝及地下厂房的安全运行，在主要建筑物表面或内部布置了变形、渗流、应力应变等较为全面的监测项目，积累了较长系列的观测资料。工程所处流域的汛期为每年7—8月份，该时段大坝水位较高，风险程度较大。为了验证本模型的有效性，根据大坝的原型观测资料和正反分析报告，选取2007年7—8月份中较高水位下的9个监测指标样本对大坝性态进行安全评价。为了便于计算，将样本实测值与数值模型计算的差值进行标准化处理，计算出该时间段大坝实测指标的量化值，具体计算过程参考文献[20]，结果见表1。

4.2 计算结果分析

4.2.1 混凝土坝性态安全评价指标组合权重计算

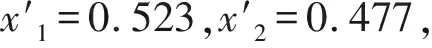
表1 混凝土重力坝实测性态各评价指标量化值 Table 1 Quantitative values of evaluation indicators of a concrete gravity dam

表2 混凝土坝评价指标权重赋值Table 2 Weight assignment of evaluation indicators of concrete dam

4.2.2 混凝土坝性态安全评价指标云模型隶属度矩阵的确定

联立式(19)—式(22)与前文构建的混凝土坝安全评价等级标准，可得到混凝土坝各评价指标安全等级的云模型参数，见表3。

表3 混凝土坝性态安全评价正态云模型参数Table 3 Parameters of cloud model for the evaluationof concrete dam safety

将计算得到的混凝土坝性态安全评价云模型参数导入到编制的MatLab程序中，得到各评价指标的隶属度并绘制相对应的云图，见图3。

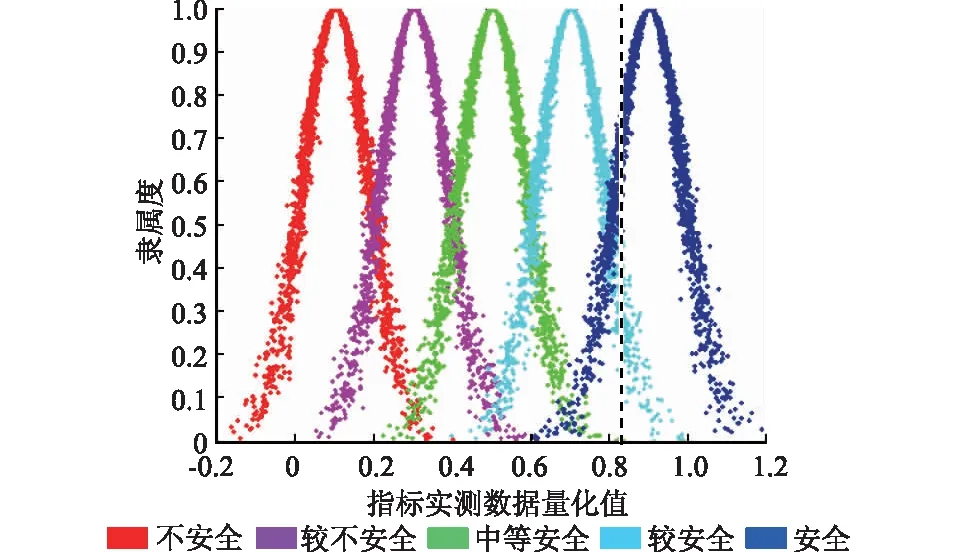
图3 混凝土坝安全评价指标隶属云图Fig.3 Membership clouds of safety evaluationindicators of concrete dam

结合表3中混凝土坝各评价指标安全等级的云模型参数，将表1中混凝土重力坝各实测指标量化值采用云模型正态发生器计算出各评价指标的隶属度矩阵R，由于云模型具有一定的随机性，本文重复计算了500次，计算了在不同隶属度情况下的平均综合值。以样本1为例，计算得到的隶属度矩阵见表4。

表4 云模型隶属度矩阵Table 4 Membership matrix of cloud model

由表4可知，以指标P1为例，安全等级Ⅰ～Ⅴ的隶属度分别为0.642，0.369，0，0，0，说明指标P1隶属于Ⅰ等级的概率最大，同时也有可能隶属于Ⅱ等级，但是可能性相对于Ⅰ等级来说较小，这与实际意义是相符的。该结果也可在图3中较为明显地表现出，指标P1落在Ⅰ级云上的较多，落在Ⅱ级云上的相对来说较少，而落在其他等级的几乎没有。同理，可得出其他样本的隶属度矩阵，由于文章篇幅有限，这里不再一一列出。

4.2.3 混凝土坝性态安全评价结果

根据计算得到的组合权重向量W和云模型隶属度矩阵R，可计算最终混凝土坝安全模糊评价矩阵：Z=W×R=(0.300, 0.625, 0.096, 0, 0)，由最大隶属度原则可知该混凝土重力坝的性态安全等级为Ⅱ级(较安全)，同理可计算出其余8组样本的评价结果。为了验证本文模型的可靠性，采用文献[14]和文献[20]中的评价方法对该坝的性态安全进行评价，并将3种评价方法的结果进行对比，详见表5。

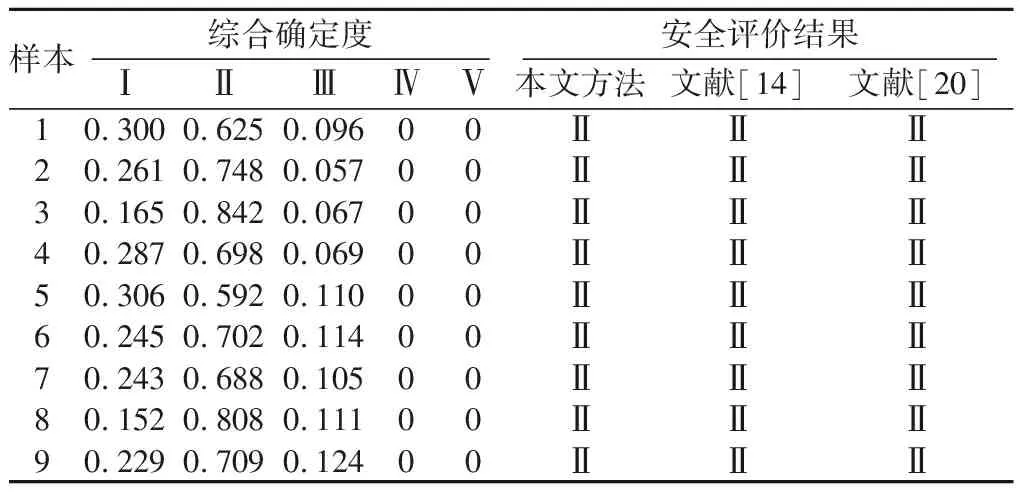
表5 大坝性态安全评价结果Table 5 Safety evaluation results for dam performance

由表5可知，本文模型对大坝性态安全判定结果为Ⅱ级，与文献[14]、文献[20]结果基本一致，且与该坝2007年的《大坝监测资料分析报告》结果相符，验证了该模型的可行性与有效性。与其他2种方法相比，本文模型的优势在于：

(1)在权重的确定上，文献[14]采用专家主观赋权和信息熵客观赋权相结合的方式对指标进行赋权，但在主、客观组合权重系数确定上认为两者同样重要，这显然过于主观，不够科学严谨；文献[20]将实测指标进行量化处理，利用向量相似度方法确定权重，客观性太强。本文模型综合考虑了主、客观因素，在单位约束条件下实现了以评价结果向量为基础的组合赋权寻优，在权重的确定上更加科学和全面。

(2)混凝土坝性态安全评价是一个多层次的复杂系统工程，评价过程中存在着模糊性和随机性，其他2种方法对于评价过程中评价指标与隶属区间的随机性和模糊性考虑不足。

本文模型引进了云模型概念，将混凝土坝安全评价过程中的随机性与模糊性转化为定量的隶属度，最终的计算结果不但对大坝的安全状态进行了判定，而且直观地表现出与其他安全等级之间的隶属关系，更具优越性。由于文章篇幅有限，文中仅选取了2007年7—8月份中水位较高的9个监测指标样本对混凝土坝性态进行安全评价，考虑到大坝安全监测是一组时效长序列监测过程，因此要对大坝进行更为长期和全面的安全评价还需以更多的监测数据为基础。

5 结 论

(1)构建了以变形、渗流和应力为主要监测项目的混凝土坝性态安全评价指标体系，综合运用基于G1法和熵权法的组合赋权理论，通过引入单位约束函数，实现了单位约束条件下性态指标组合赋权的寻优，使指标的赋权更加科学和全面。

(2)引入了云模型概念，通过期望(Ex)、熵(En)、超熵(He)3个特征参数，将大坝性态安全评价中评价指标的随机性与隶属区间的模糊性转化为定量的隶属度，实现了定性概念和定量数据间的相互转换，弥补了传统评价方法在评价过程中对不确定性考虑的不足。

(3)以运行期混凝土重力坝为对象，选取汛期高水位下监测数据作为本文模型的指标样本对大坝性态进行安全评价。评价结果与其他方法结果基本一致，并与大坝实际情况相符，验证了该方法的有效性与可行性，同时也为大坝运行性态安全评价提供了一条新的思路。