机车曲线通过的动态模拟方法研究

陈 阳， 周文祥， 王晨晨， 陈 晓, 文永翔， 张晓阳

(1 西南交通大学 牵引动力国家重点实验室， 成都 610031；2 中车株洲电力机车有限公司， 湖南株洲 412001)

一般而言，机车车辆由直线轨道进入曲线轨道时，由于存在着保持其原有行驶方向的惯性，需要依靠轮缘在外侧钢轨的引导下，才沿着曲线轨道行驶，因此曲线通过时轮轨间产生的轮缘力和侧压力比较大，由此产生的轮缘磨耗和钢轨磨耗也比较大，严重的甚至会导致机车脱轨引发安全事故。

由于曲线通过的复杂性以及技术有限等原因，有关曲线通过的模拟至今还没有较为完善的方案。现有的滚动振动试验台主要模拟了超高不足以及内外轨长差[1-5]，可以粗略地模拟圆曲线通过时的轮轨关系。但是就缓和曲线段而言，超高、曲率等参数都在不断地变化，因此缓和曲线的动态模拟仍有待研究。基于此，文中研究了一种动态横移轨道轮单元的方法，并通过仿真分析验证了本试验方法的可行性。

1 机车曲线通过分析

由于地势地形的限制，铁路线路难免会出现曲线。据统计[6]，在我国的铁路营业路网总里程中，曲线线路约占40%，而曲线通过的相关问题正是研究车辆横向动力学的核心所在。具有良好曲线通过性能的车辆在曲线上运行时轮轨相互作用力小、磨耗小，从而减少了机车的牵引力,节约了能耗，同时减低了线路维修工作量，使行车更加安全。

曲线线路中超高的设置，是为了机车自身的重力分力抵消曲线上行驶时的离心力，满足旅客的舒适度，提高曲线通过的安全性。于轨道而言，超高的设置有利于均衡内、外两股钢轨的受力和垂直磨耗情况。

完整的曲线线路包括3个部分：直线、缓和曲线和圆曲线。若机车匀速运行，在圆曲线段通过时，由于线路的曲率半径、超高为定值，其受到的离心作用也为定值。为了避免曲率半径、超高等参数的突变，减少机车车辆在分界处的轮轨冲击，因此在直线和圆曲线之间需设置缓和曲线。需要指出的是，由于缓和曲线段的曲率、超高等都在逐渐地发生变化，因此对相关模拟机构的控制有较高的精度要求。

2 曲线线路的动态模拟

为了模拟机车在曲线通过时的运行情况，关键的是利用滚动振动试验台进行模拟曲线线路。由于物体的分运动之间相互独立、互不影响，为了使曲线通过的研究更加直观，文中将曲线线路的特征分为：内外轨长度差、外轨超高、线路不平顺以及曲线曲率4个部分进行分析。

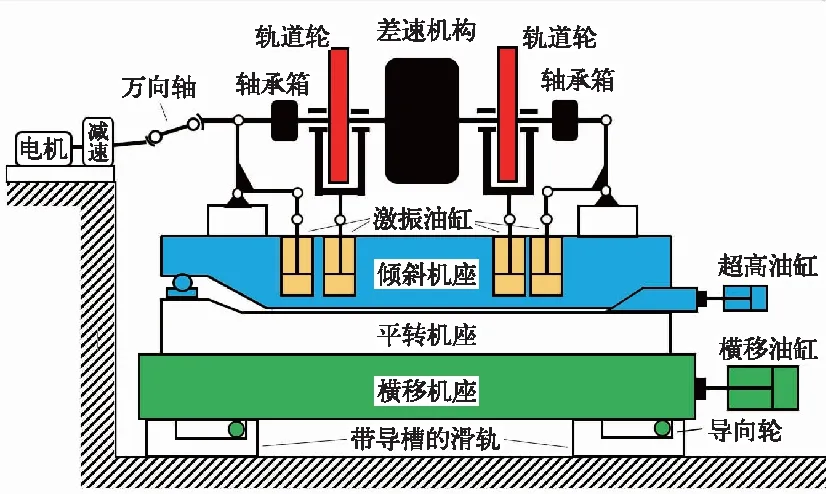
图1 轨道轮单元的结构示意图

2.1 内外轨长度差的模拟

由于曲线线路上外轨的长度大于内轨，因此可以通过旋削轨道轮或者在轨道轮之间设置机械差速装置的方式模拟内外轨的长度差。根据GB 50090-2006《铁路线路设计规范》，我国曲线线路常用的缓和曲线是三次抛物线型[7]，其曲率的变化为线性。设x为机车在曲线线路上运行时的纵向坐标，xl0为缓和曲线段投影在x方向的总长度，R为圆曲线的半径，则缓和曲线段的瞬时曲率半径的表达式为：

(1)

为了将直线、缓和曲线、圆曲线的公式统一表达，并利于相应的控制，引入参数e：

(2)

假设车辆的行驶速度为v0，两轨顶中心间的距离为2d(取1 500 mm)，轨道轮半径为r，则外侧车轮速度为：

(3)

内侧车轮速度为：

(4)

对应外侧轨道轮转速为：

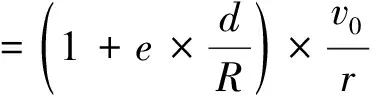
(5)

内侧轨道轮转速为：

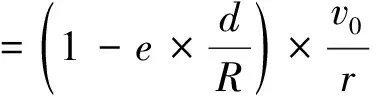
(6)

考虑到缓和曲线段的内外轨的长度差不断发生变化并逐渐增大，文中采用机械差速装置，其机械原理如图2所示。

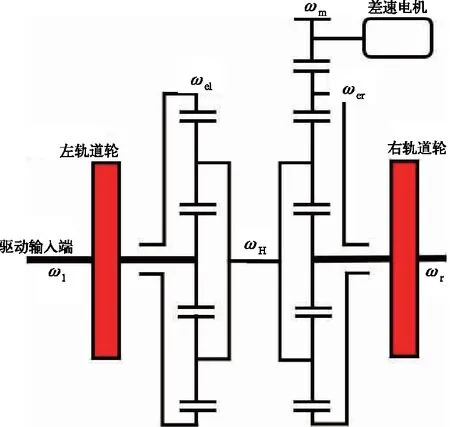
图2 差速机构原理图

由图2可知，左、右轨道轮间的差速结构由两组对称布置的行星轮系对称构成，并且对应齿轮的齿数相同，根据行星轮系的运动学公式，可得两组行星轮系的相对转速比为：

(7)

(8)

若左边轨道轮模拟的是内侧轨道，根据式(5)和式(6)，则左右轨道轮的转速之差：

(9)

由式(8)和式(9)，可以推出差速电机的转速需满足：

(10)

2.2 外轨超高的模拟

利用超高油缸调整楔形块的位置，然后推动整个倾斜机座产生一定的倾斜角度，从而可以模拟外轨超高。设圆曲线段的超高为h0，缓和曲线段采用直线型超高顺坡，即缓和曲线段内的超高变化为线性，则整条曲线模拟时的超高可以表示为：

h(x)=eh0

(11)

超高角γ为：

(12)

值得一提的是，传统的方案是通过设置未平衡超高来模拟超高和离心力的共同作用，而文中研究的方案则把超高和离心力分别进行模拟：超高的模拟与实际线路的超高设置相同，通过横移油缸的加速横推实现离心力的模拟。

2.3 线路不平顺的模拟

线路不平顺是由于左、右轨道的横向和垂向误差造成的，主要包括轨向不平顺、轨距不平顺、高低不平顺、水平不平顺。通过横向及垂向油缸的激振，进行模拟线路的扰动。为了更符合中国铁路线路不平顺的实际情况，文中采用陈宪麦[8-9]等人建议的我国铁路干线通用轨道谱，其表达式如下：

(13)

式中：S(f)为谱密度，(mm2·m)；f为空间频率(1/m)；其中速度为120 km/h的轨道谱对应的不平顺激励，如图3所示。

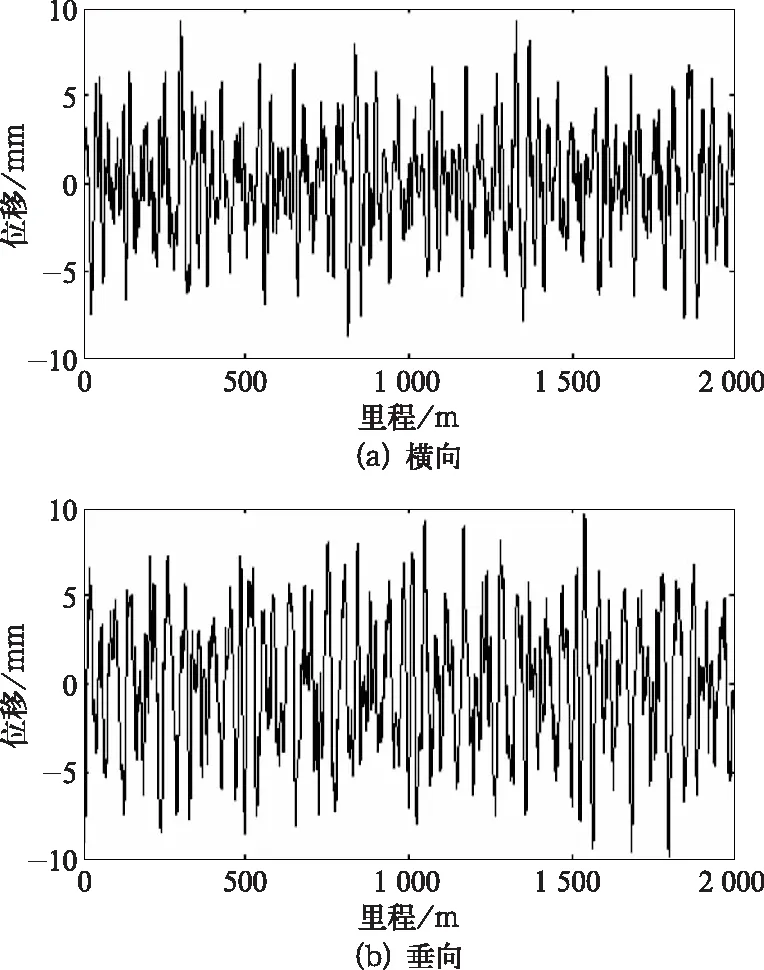
图3 轨道不平顺激励图

2.4 曲线曲率的模拟

为了模拟被测试机车在对应的曲线线路上，利用滚振台再现机车曲线通过时的离心作用及轮轨接触关系，文中分析了一种加速横推的方法：通过大功率的横移油缸，推动横移机座上的导向轮在特定形状的导槽中移动，从而推动整个轨道轮单元实现特定轨迹的横移。导槽的作用，一方面要实现曲线线路在y方向不断横移的特征，从而可以模拟曲线通过时的离心作用；另一方面还要保证轨道轮时刻处在对应曲线线路的切线方向，更接近真实的轮轨接触关系。由此可见，导槽的形状是模拟曲线通过的关键。

设l0为缓和曲线的长度，三次抛物线型缓和曲线段的支距公式如下：

(14)

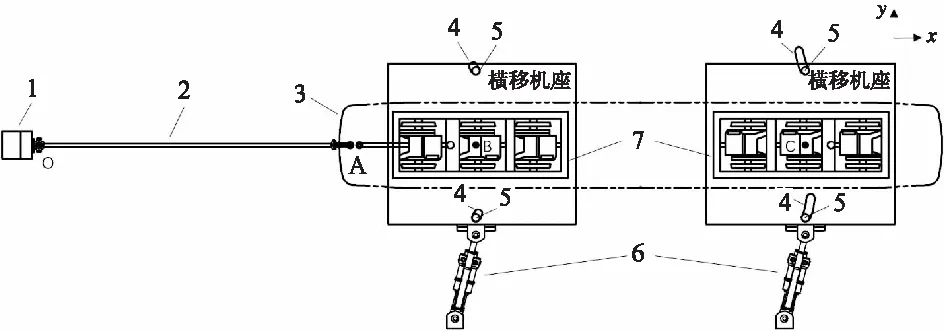
1-反力座；2-拉杆；3-车体；4-导槽；5-导向轮；6-横移油缸；7-轨道轮单元。图4 滚动振动试验台工作原理图

则缓和曲线的切线偏角θ(缓和曲线上的切线与ZH点处切线的夹角)可以表示为：

(15)

在缓和曲线段，由机车的运行速度可以求得运行的里程，即已知参数往往是弧长S，所以取微元ds，根据高等数学微积分可得：

(16)

由于上述积分不可积，因此用幂级数展开多项式并积分可得：

(17)

假设机车匀速运行，由公式(17)和(14)，可得弧长S与横纵坐标x，y之间的关系，因此可以确定机车在缓和曲线任一时刻的横向位移y；根据公式(15)则可得此时此刻对应曲线的切线偏角θ。

圆曲线段的相关计算较为简单：利用HY点的横纵坐标x，y和切线偏角θ，再根据圆曲线的半径R,可以求得圆心的位置。因为圆曲线段的圆心位置固定不变，通过弧长S即可求得圆曲线段任一点的横向位移y和切线偏角θ。

3 曲线通过安全性仿真分析

文中利用SIMPACK软件建立了机车在真实曲线线路和滚振台试验的模型。曲线线路的关键参数有：圆曲线半径R(m)、缓和曲线长度L0(m)、超高h(mm)及行车速度v(km/h)。依据GB 50090-2006《铁路线路设计规范》和GB 50157-2013《地铁设计规范》[10]，选取R=600 m，L0=80 m，h=120 mm的情况为例，对本研究方法进行仿真分析。文中建立的滚动振动试验台有关曲线通过安全性的仿真模型，如图5所示。

图5 试验台仿真模型

线路上的轮-轨接触关系类似于点-面接触，而试验台上的轮-轮接触更近似于点-点接触，这是因为轨道轮的外周存在一定的曲率，导致轮-轮接触的接触斑小于轮-轨接触。根据Kaller的线性接触理论：接触斑的面积较小时，对应的蠕滑系数也较小，进而将影响轮-轨(轮-轮)间的相互作用力。

图6 接触斑面积比较

由图6可知，试验台仿真的接触斑面积和线路仿真的变化规律相似，整体呈现随运行速度增大而增大的趋势，并且当运行速度进一步增大时，试验台和线路上接触斑面积的差距将会缩小，这是因为轮-轨(轮-轮)间的相互作用增强，轨道轮曲率的影响将减弱。

研究曲线通过安全性的主要指标有轮轨横向力、垂向力，脱轨系数等。通过SIMPACK软件的仿真分析，以起导向作用的一位轮对的外侧车轮为研究对象，机车运行速度不变，然后计算其横向力与垂向力之比，并选择其中的最大值作为脱轨系数，仿真结果如图9所示。

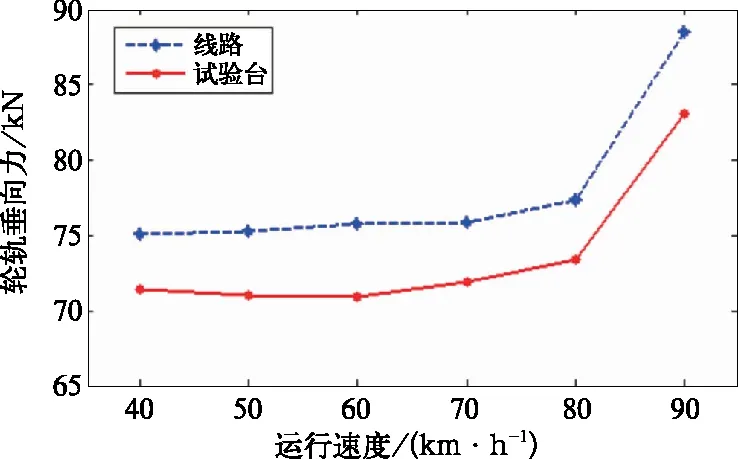
图7 轮轨垂向力

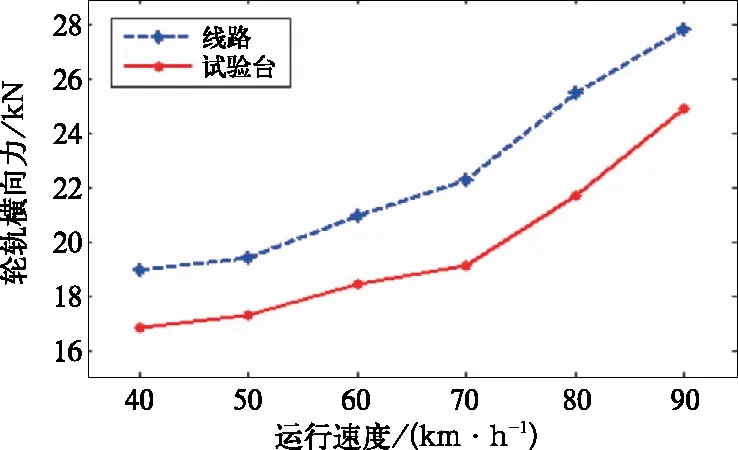
图8 轮轨横向力

图9 脱轨系数

由图7、图8和图9可知，试验台曲线通过仿真的结果与曲线线路的变化规律基本一致。以速度为70 km/h的情况为例：线路上的轮轨垂向力为75.88 kN，试验台上为71.95 kN，误差为5.2%；线路上的轮轨横向力为22.30 kN，试验台上为19.12 kN，误差为14.3%；线路上的脱轨系数为0.413，试验台上为0.390，误差为5.6%。

软件仿真分析的结果表明：试验台模拟曲线通过性能与曲线线路上的存在一定的误差，轮轨垂向力与脱轨系数的误差均在6%左右；因为试验台两端限位拉杆的约束，导致试验台与线路上的轮轨横向力的差异较大，但在二者间的差异较为固定，并不会随着速度的增大而增大，经过修正后仍有很高的参考价值。由此可知，利用滚动振动试验台动态模拟机车曲线通过的过程，可以为曲线通过的理论研究以及新型转向架的开发提供试验数据，使试验更加安全。

4 结束语

(1)分析了一种曲线通过的动态模拟方法：根据曲线线路特征，通过机械差动装置模拟内外轨长度差；通过超高油缸推动楔形块模拟外轨超高；通过横移油缸推动轨道轮单元在导向槽内移动，使轨道轮时刻处在对应曲线线路的切线方向，并实现曲线不断横移的特征；通过横向、垂向油缸的激振，模拟轨道不平顺。

(2)通过软件的仿真分析，得出台架试验与线路运行时的曲线通过性能变化规律一致，误差较为固定，经过一定的修正后台架试验可以接近曲线线路上的运行状况。因此，从理论的角度分析，文中研究的有关曲线通过动态模拟的方法是可行的，但从工程实用的角度分析，利用滚动振动试验台动态模拟机车曲线通过的方法还有待于进一步的改进和完善。

(3)由于研究的曲线通过动态模拟方法指的是机车由直线经过缓和曲线进入圆曲线这一完整的过程，弥补了现有技术方案只能粗略模拟圆曲线的不足。研究结果为在建的滚动振动试验台的设计提供了参考，为动态模拟曲线通过的台架试验提供了依据。