基于QPSO优化模糊—SVM的电站锅炉燃煤结渣特性预测

任 林，王东风

（华北电力大学，河北 保定 071000）

0 引言

电站锅炉受热面结渣问题会影响锅炉运行的安全性、经济性与可靠性，甚至会导致恶性事故的发生。改革开放以来中国经济飞速发展，电站锅炉容量逐步增大，锅炉燃煤的种类也日益增多，这些因素都使电站锅炉受热面结渣问题更加突出。因此精确判断电站锅炉的结渣程度，并做好相应的事故预案，对于防止事故发生、加强运行经济化具有重要意义［1］。

目前基于煤灰特性的电站燃煤结渣程度的预测模型有单一指标预测模型、综合指标预测模型以及多指标预测模型。单一指标预测模型是利用单一的某个煤灰物理特性或煤灰成分特性对锅炉结渣情况进行预测，此方法运算简单、快速，但存在准确率偏低的问题［2］。 综合指标预测模型中，徐乾等人［3］提出应用综合指标R来预测燃煤的结渣特性，综合指标预测模型与单指标预测模型相比提高了锅炉结渣特性预测的准确率，但也不能完全准确预测锅炉的结渣特性。多指标预测模型中，王洪亮等人［4］将模糊数学与神经网络结合，训练出一个模糊神经网络模型，进行燃煤结渣特性预测，这个方法能比较准确地预测结渣特性，但此方法需要较多的训练样本，在现实中通常电站锅炉的燃煤结渣数据量较小。王宏武等［5］应用模糊C聚类法（FCM）预处理锅炉燃煤结渣数据，然后通过SVM建立锅炉燃煤结渣程度预测模型，但该方法在FCM的聚类中心的选择与聚类指标的选择对分类结果影响较大，要达到较高的分类正确率，需要进行大量的分组实验。杨冬等人［6］根据1 000 MW超超临界锅炉的实际运行数据，基于煤灰特性，分别建立了单一指标与综合指标的锅炉结渣特性预测模型，虽然这些预测模型能快速地预测电站锅炉的结渣特性，但当锅炉采用燃用煤质不均匀或混煤燃烧时，这些模型预测准确度下降。陈红江［7］提出了一种基于突变级数理论的电站燃煤锅炉结渣特性的预测方法，在确定电站锅炉结渣特性的影响因素后，对各因素的影响程度进行排序，并确定各因素指标体系，最终求出各个样本的突变级数，从而完成对电站锅炉燃煤结渣等级的划分。

本文在上述研究的基础上，利用模糊数学理论，将5种模糊隶属度函数与支持向量机 （SVM）相结合，构成模糊-SVM模型，并应用量子粒子群算法（QPSO）优化隶属度函数的参数。为了提高预测的准确度与可信度，将5个训练完成并达到最优参数的模糊—SVM模型看作5个专家系统，测试样本分别输入这5个模型中，模型的输出采用投票机制，根据投票结果判断测试样本的结渣程度。

1 电站燃煤锅炉结渣的模糊—SVM模型

1.1 结渣影响因素的确定

电站燃煤结渣是一个复杂的物理化学反应过程［8］。根据实际情况，综合考虑煤质特性与锅炉的工况特性，选取7个主要影响因素作为本文研究电站燃煤结渣的指标。分别是：煤的软化温度t2、硅铝比m（SiO2）／m（Al2O3）、碱酸比 B／A、硅比 G、综合指数R、无因次炉膛实际切圆直径Dw以及无因次炉膛最高温度tw。7个指标的定义为：

燃煤软化温度t2为煤在加热到高温时的熔融特性。 硅铝比m（SiO2）／m（Al2O3）为煤灰中酸性氧化物SiO2与碱性氧化物Al2O3的质量比。

硅比

酸碱比

综合指数

无因次炉膛平均直径

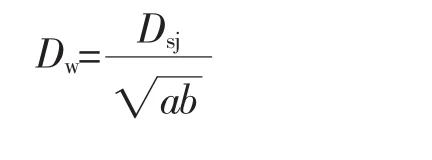
无因次炉膛最高温度

式中：Dsj为实际切圆直径；a，b分别为炉膛的深与宽；Tpj为炉膛平均温度。

1.2 隶属度函数与指标模糊化

电站燃煤结渣程度是一个模糊化的概念，“轻微”“中等”以及“严重”均为没有明显界限的模糊化词语。选取的5个隶属度函数分别为三角形隶属度函数、梯形隶属度函数、半圆形隶属度函数、柯西隶属度函数和斜线形隶属度函数，应用上述5种隶属度函数将输入变量模糊化，作为支持向量机的输入。隶属度函数参数的选择包含较多人为因素，因此，优化隶属度函数的参数可以很大程度上提升预测模型的准确度［9］。5种隶属度函数的图形与函数表达式如下所示。

1.2.1 三角形隶属度函数

在三角形隶属度函数（以等腰三角形为例）中需要优化的参数为式（1）中b与z1的取值，其中，b为等腰三角形底边长的一半，z1为等腰三角形顶点所对应的x值。

图1 三角形隶属度函数

三角形隶属度函数的表达式为

1.2.2 梯形隶属度函数

梯形隶属度函数（以等腰梯形为例）需要优化的参数为式（2）中 a1，a2与 z2的取值。

图2 梯形隶属度函数

梯形隶属度函数的表达式为

1.2.3 半圆形隶属度函数

半圆形隶属度函数需要优化的参数为图3中r与z3的取值。

图3 半圆形隶属度函数

半圆形隶属度函数的表达式为

1.2.4 柯西隶属度函数

柯西形隶属度函数需要优化的参数为式（4）中的z4，d1的取值，如图4所示。

图4 柯西形隶属度函数

柯西形隶属度函数的表达式为

1.2.5 斜线形隶属度函数

斜线形隶属度函数需要优化的参数为图5中z与式（5）中的 d2的取值。

斜线形隶属度函数的表达式为

图5 斜线形隶属度函数

1.3 支持向量机（SVM）

支持向量机算法（SVM）是由 Vapnik 等人［10］在20世纪90年代提出的一种机器学习算法，目前已经成为诸多领域的重要研究工具，其在模式识别与数据挖掘等领域应用尤其广泛［11-12］。

支持向量机可分为线性支持向量机与非线性支持向量机，但由于大多数问题都是非线性的，故非线性支持向量机应用更加广泛。非线性支持向量机的原理如下。

非线性支持向量机的基本思想是对输入变量x进行非线性变化，用过高斯函数将其转换到高维空间，然后通过空间的变换求得最优分类平面。对于实际应用中的线性不可分情况，在条件中引入松弛项，将约束条件放宽，那么，非线性支持向量机则转换为下面的最优问题：

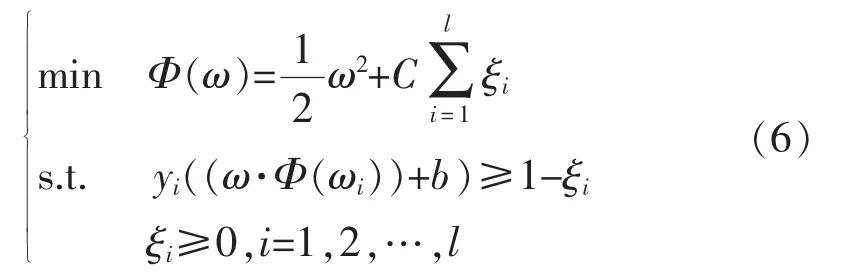
式中：C为惩罚因子，C值越大惩罚力度越重；b为分类平面截距，取值可参见文献［13］；松弛变量ξi为衡量样本被错分的度量。应用拉格朗日求极值方法与 KTT条件（Kuhn-Tucker Conditions），可以将上述问题转换为对偶问题。

式中：α为拉格朗日因子。

支持向量机的一个重要特征就是解具有稀疏性，只需要少量样本即可解决分类问题，适合解决小样本问题。支持向量机结构简单，学习性能好，泛化能力较强，适合解决小样本、非线性、局部极小点等问题。

2 量子粒子群算法

粒子群算法 （PSO）是由Kennedy J和Eberhart R.Particle在1995年提出的一种模仿智能动物智能集体行为的算法［14］。粒子群算法虽然具有较强的优化能力，但它不是一个全局收敛算法，在全局搜索能力上对速度上限过于依赖，从而降低了粒子群算法的鲁棒性，这些缺陷常使粒子群的优化结果并不是问题最优解。2004年，Sun等人针对粒子群的缺陷将量子理论与PSO算法相结合提出了量子粒子群优化算法（QPSO）［15］。 量子粒子群算法在原理上与粒子群相似，都是基于更新个体最优与种群最优的信息进行迭代。与粒子群算法不同的是，量子粒子群算法中的粒子都是以量子的行为方式运动，每个粒子可以概率地出现在解空间中的任意位置，这增强了粒子的运动随机性，还提高了算法的全局寻优能力［16］。

量子粒子群算法（QPSO）是基于量子力学提出来的一种改进粒子群算法［17］。量子空间的粒子中存在某种吸引势，使得粒子运动中心产生束缚态，这种束缚态让粒子满足聚集态性质。量子粒子群算法与标准粒子群算法存在一个主要的区别就是，量子粒子群算法中的粒子只包含位置信息而不包含速度信息［18］。量子粒子群的进化方程为：

式中：M 为粒子种群的个数；d为维数；Xid（t）为第 t次选代时第i个粒子d维值；mbest为当前所有粒子最优值和的平均值；pbest，i为第i个粒子的历史最优值；φ 与 u 为在［0，1］上服从均匀分布的数；Pid（t）为 t次粒子迭代时第i个粒子d维的个体最优值；pgd（t）为第t次迭代时的全局最优值；β为收缩—扩张系数。通过改变β的值可以改变QPSO收敛速度，改善QPSO的全局搜索能力，β前符号“+”和“-”概率各占50%，β可由（11）计算得到：

式中：T为最大迭代次数；t为当前迭代次数。

图6为量子粒子群算法的流程。

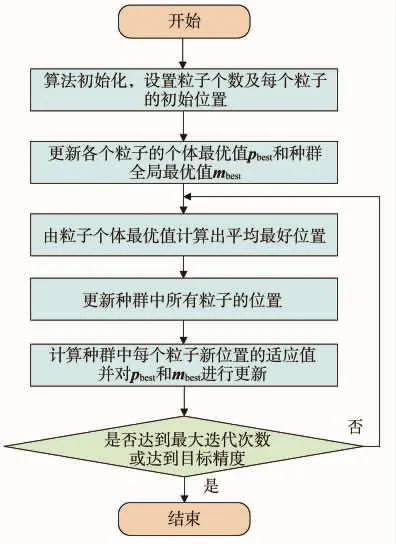
图6 量子粒子群算法的流程

3 基于模糊—SVM的燃煤结渣预测

3.1 模型参数设置

选取上述5种隶属度函数，将7个判别指标模糊化后输入支持向量机中，模型的输出以1，2和3代表结渣程度“轻微”“中等”和“严重”。并用量子粒子群算法优化隶属度函数的参数。

为验证本文提出模型的有效性，选取40组电站燃煤作为样本，其中30组为训练样本，10组为测试样本，样本数据来自文献［19-20］，表1为测试样本数据。初始模糊—SVM模型中的隶属度参数来自文献［19］，采用量子粒子群算法优化后的隶属度参数如表2～6所示。所有模型中SVM算法的惩罚因子Cs与核函数gs采用交叉验证法得到，量子粒子群算法优化的模糊—SVM模型中，量子粒子群算法的粒子数N为50，最大迭代次数为100。

表1 10组测样本数据

3.2 实验结果与分析

量子粒子群算法优化后的各隶属度函数参数如表2～6所示。通过表2～6可以看出，不同类型隶属度函数对应的最优参数有较大差别，这与隶属度函数本身特性有关，也与量子粒子运动的随机性有关。

将10个测试样本的7指标依次输入模糊—SVM模型与QPSO优化后的模糊—SVM模型中，预测结果及正确率如表7～8所示，其中标注“*”的样本代表预测错误。通过表6～7可以看出，QPSO优化后的模糊—SVM模型的预测正确率显著提高，其中三角形隶属度函数、半圆形隶属度函数与斜线形隶属度函数对应的模糊—SVM模型的正确率达到100%，梯形隶属度函数与柯西形隶属度函数对应的模糊—SVM模型的正确率达到90%与80%。这说明，经过量子粒子群算法优化后的模型正确率更高，更适合应用于电站燃煤结渣预测。

表2 三角形隶属度函数最优参数

表3 梯形隶属度函数最优参数

表4 半圆形隶属度函数最优参数

表5 斜线形隶属度函数最优参数

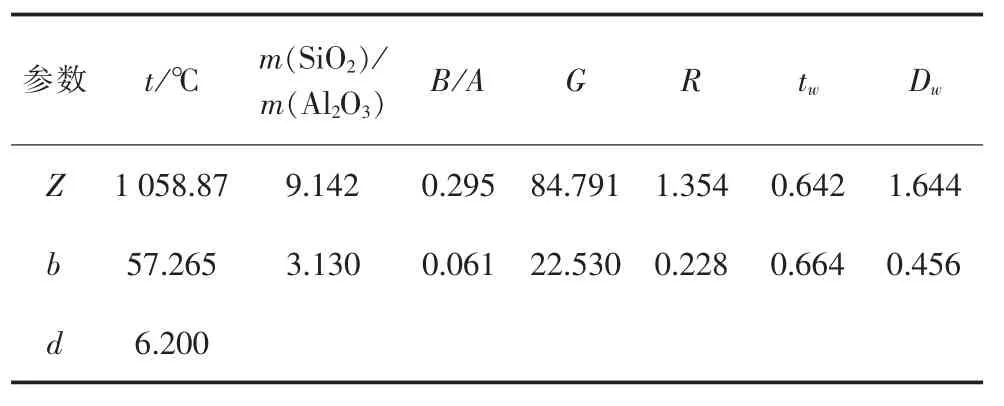
表6 柯西形隶属度函数最优参数

将5个经过量子粒子群算法优化后的模糊—SVM模型看作5个专家预测系统，在预测实际生产中燃煤结渣程度时，采取投票机制进行判断。其中，三角形隶属度函数、半圆形隶属度函数与斜线形隶属度函数对应的模糊—SVM模型的可信度为100%，在投票时权重为1；梯形隶属度函数对应的模糊—SVM模型可信度为90%，在投票时权重为0.9；柯西形隶属度函数对应的模糊—SVM模型可信度为80%，投票时权重为0.8。

表7 10测试样本模糊—SVM模型预测结果

表8 10测试样本QPSO优化后模糊—SVM模型预测结果

通过表6～7可以统计出，在10个测试样本中，样本序号为5，7，8的3个样本被预测错误的频率最高。将测试样本序号为5，7，8的燃煤结渣指标输入5个专家预测系统，并采用投票机制判断结渣程度。采取投票机制的预测结果与实际结渣情况对比如表9所示。投票机制的优点是判断时采用的信息更全面，预测的准确度与可信度均高于单一模型。

表9 投票机制预测结果与实际结渣情况对比

4 结语

针对电站燃煤结渣程度问题，采用量子粒子群算法优化的模糊—SVM模型进行预测。应用实际电站锅炉结渣数据检验模型预测，检验结果表明采用QPSO优化后的模糊—SVM模型与传统模糊—SVM模型预测的准确率更高。

针对出错率较高的3个测试样本，将QPSO优化后的5个模糊—SVM模型组成一个专家系统，通过投票机制综合判断电站燃煤结渣程度，实验结果表明，这种预测方式更加可信，准确度更高。