不同挟沙力公式在新疆托帕水库的应用分析

姚鹏亮

（新疆水利水电勘测设计院研究院，新疆 乌鲁木齐 830000）

水流挟沙力是指在一定的水流条件及边界条件作用下，水流能携带泥沙通过河段下泄的沙量[1]。天然河道总是处于冲淤交替的动态演变过程中，当携带泥沙的水流到达某一河段时，若该河段的水流挟沙力小于来水，则会通过泥沙落淤进行减载，进而抬高河床，减少水深，增大比降，河道向不淤积转化，反之，河道向不冲刷转化。采用合适的数学模拟公式对水流挟沙力进行计算，是掌握河流淤积动态演变过程的重要手段，本文针对不同挟沙力公式在新疆托帕水库中的应用进行分析。

1 工程概况

恰克玛克河中下游植被差，洪水季节，水流汇集过程中，将中、低山区第三纪松散沉积物通过河网汇流、坡面汇流过程源源不断地向下游携运。恰克玛克河具有水少、沙多的特点，实测多年平均含沙量为9.87 kg/m3，为内陆河塔里木河的2倍。托帕水库库沙比Kt为40.9，面临严重的泥沙淤积问题。水库设计时以下游的恰其噶为参证站，计算出坝址断面多年平均径流量为1.725亿m3，多年平均输沙量为159.1万t，泥沙主要集中在汛期4月～9月，占全年的99%，年际变化大。

2 泥沙颗粒级配曲线数据

2.1 悬移质泥沙颗粒级配曲线数据

本次在恰其嘎水文站实测泥沙系列中选择悬移质输沙量较大的2005年进行泥沙颗粒级配分析，其悬移质颗粒级配成果如图1所示，主要由粒径1mm以下的颗粒组成，包括沙、粗粉土、细粉土和粘土。其中1 mm～0.05 mm沙约占19%，0.05 mm～0.01 mm粗粉土约占47%，0.01 mm～0.005 mm的细粘土约占15%，0.005 mm以下的粘土约占18%，粒径较细，为水流挟带及排沙创造了有利条件，其干容重为1.30 t/m3[2]。

2.2 河床颗粒级配曲线数据

在托帕水库坝址处采用体积法取1 m×1 m×1 m的试坑，对大于100 mm的颗粒采用尺量法，小于100 mm采用筛析法进行床沙颗粒级配实验，托帕水库坝址的床沙颗粒级配曲线成果见图2。

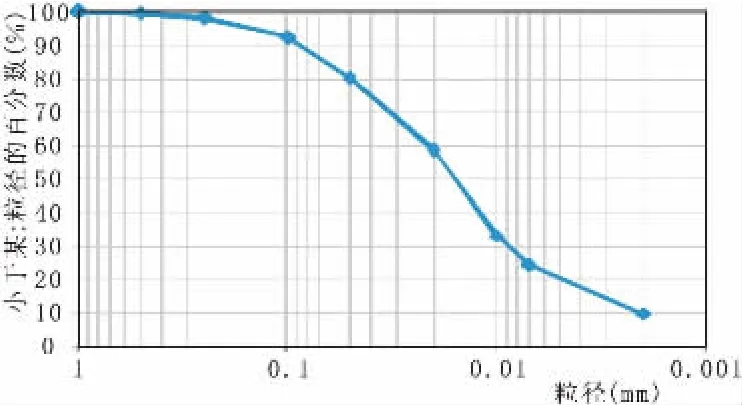
图1 恰其嘎水文站泥沙颗粒级配曲线

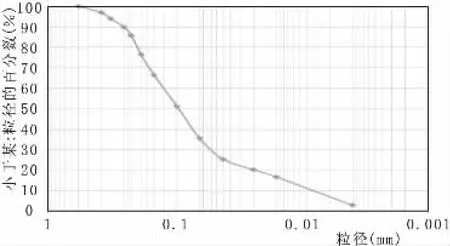
图2 托帕水库坝址附近床沙颗粒级配曲线

3 挟沙力公式

从上世纪50年代开始，国内外学者通过不断地探索和研究，根据天然河流、水库和渠道的泥沙资料，总结出适用全部悬移质泥沙的经验与半经验公式。本次选取适用于高含沙量的计算公式进行分析，见表1[3]。以下式中:S*为挟沙力；V为流速；g为重力加速度；R为水力半径；ρm为浑水密度；ω为泥沙沉速；γs为泥沙颗粒容重；γm为浑水容重；D50为床沙中值粒径。其他参数见表1。

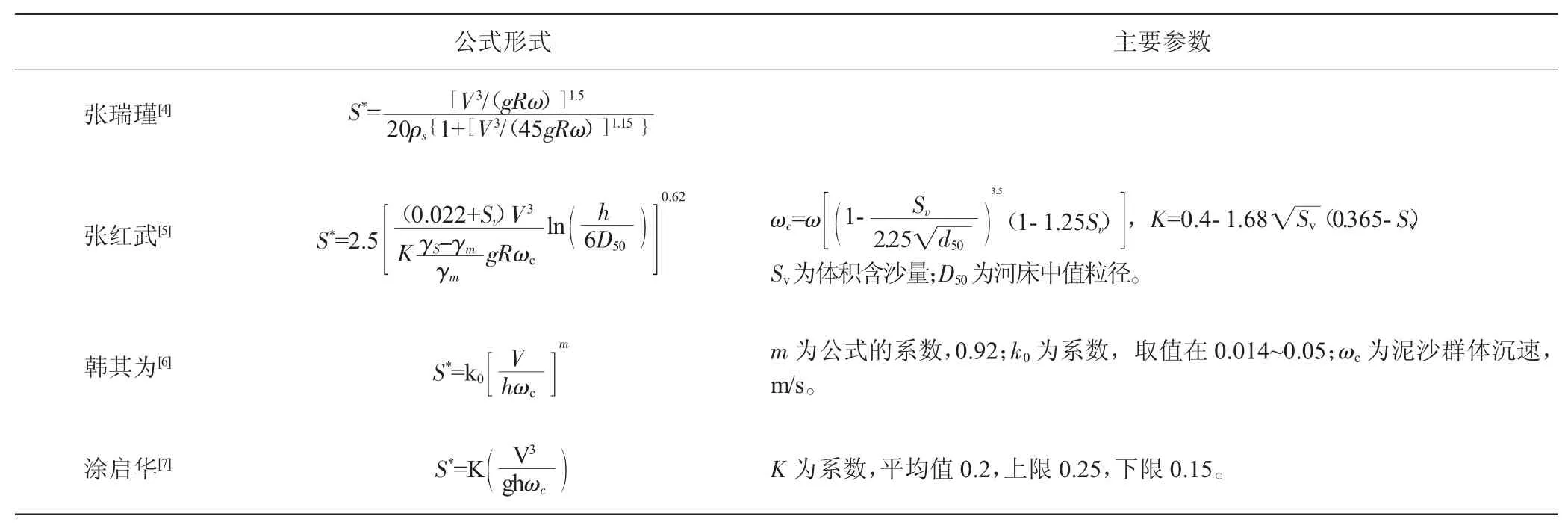
表1 水流挟沙力公式列表

4 计算成果及分析

4.1 成果合理性

采用两种方法验证水流挟沙力计算结果:（1）将计算值与实测含沙量值点绘于同一幅图中，与45°线进行比较。该方法简便易行，能直观地看出各挟沙力公式的计算成果；（2）相关系数法，即:

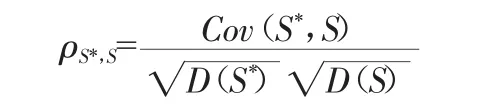
式中:ρS*，S为水流挟沙力公式计算值与实测值的相关系数；Cov（S*，S）为水流挟沙力公式计算值与实测值协方差；D（S*）为挟沙力计算值方差；D（S）为挟沙力实测值方差。

4.2 结论分析

各挟沙力计算公式的验证结果见图3～图7。

验证结果表明，韩其为和涂启华挟沙力计算成果较接近。含沙量小于20 kg/m3时，这两个挟沙力公式计算值大于实测值；含沙量大于20 kg/m3且小于100 kg/m3时，这两个挟沙力公式的计算值与实测值较为接近；含沙量大于100 kg/m3时，这两个挟沙力公式的计算值小于实测值。含沙量小于30 kg/m3，张瑞瑾[4]的挟沙力公式计算值大于实测值，含沙量大于30 kg/m3时，该公式计算成果与实测值接近，但是带宽较大。张红武[5]公式计算结果均匀分布于45°线两侧，且带宽较小，计算挟沙力和实测含沙量结果符合较好。

从公式结构分析，产生这种现象的主要原因是，韩其为[6]与涂启华[7]均为S*=f（V，h，ω）形式，参数基本相同，仅系数不同，所以成果相近。张瑞瑾增加了一个考虑参数浑水密度的ρm，计算值比韩其为、涂启华更接近实测值。张红武考虑了浑水流速分布相关的卡门常数k，考虑了床沙中值粒径D50，这些变量的引入使张红武的公式计算成果更能反映含沙量的真实值。

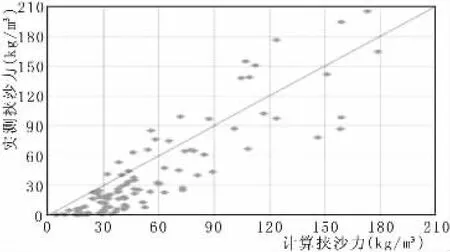
图3 张瑞瑾挟沙力计算验证图

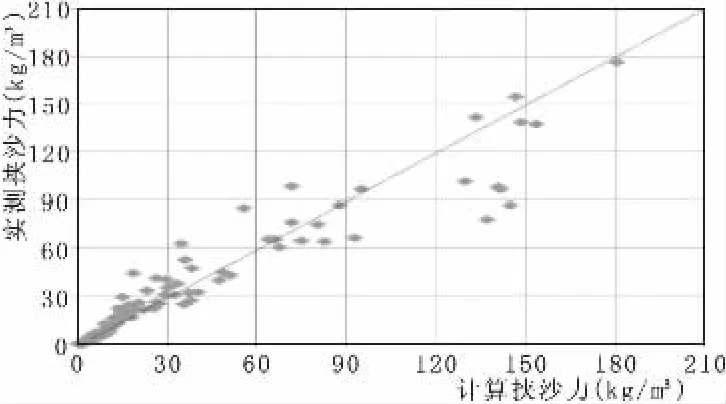
图4 张红武挟沙力计算验证图

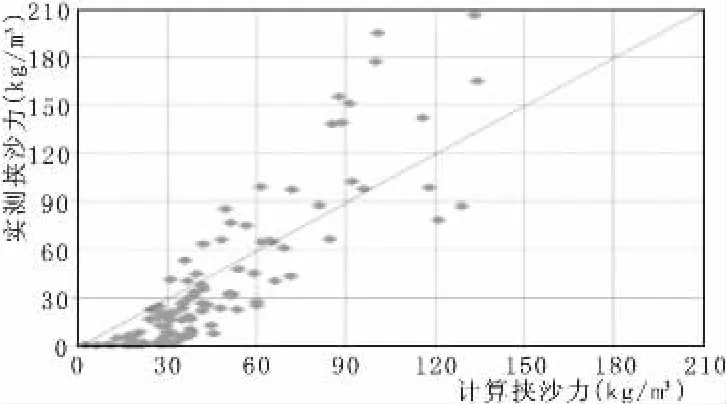
图5 韩其为挟沙力计算验证图

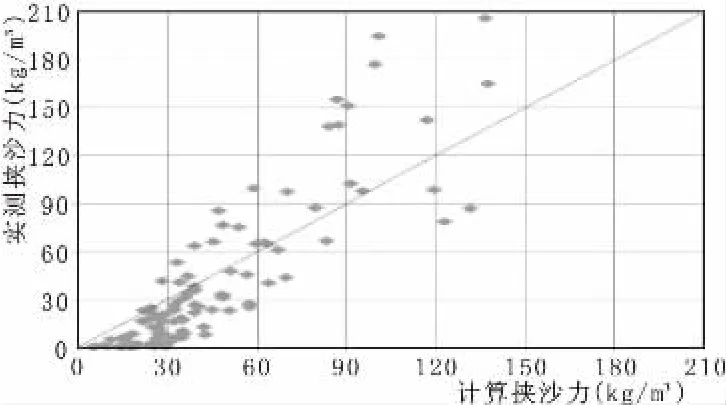
图6 涂启华挟沙力计算验证图

采用相关系数法计算:张红武公式的相关系数为0.89；张瑞瑾的为0.78；涂启华的为0.77；韩其为的为0.76。由统计学原理可知，相关系数越大，表明计算值与实测值越接近。按照相关系数进行排序，从优到劣依次为:张红武、张瑞瑾、涂启华、韩其为。综上所述，张红武公式计算值与实测资料符合最好，推荐为托帕水库冲淤计算的水流挟沙力计算公式。

5 结论

不同的河道具有不同的特性，天然河流挟沙力问题复杂，考虑到理论研究的局限性，通过积累太量实测得出的半经验半理论公式往往具有更高的精度。托帕水库所在的恰克玛克河含沙量较大，冲淤计算结果对库容产生直接影响，对相关参数进行全面分析整理至关重要。本文结合恰克玛克河托帕水库段具有代表性的实测数据，采用相关系数法对各个水流挟沙力计算公式在泥沙冲淤计算中的应用加以验证，结果表明张红武20世纪初提出的公式精度最高，具有非常大的应用价值。