考虑流固耦合的排水沟道力学计算方法

柴鹏翔

（宁夏大学土木与水利工程学院，宁夏 银川 750021）

0 引言

流固耦合问题在工程应用中随处可见，因此对于流固耦合问题的研究具有很大的价值，诸如石油运输过程中，石油与管壁的流固耦合问题；核能作为一种清洁又高效的能源倍受重视，反应堆运行以及核燃料的贮存都涉及到流固耦合的问题[1]；对水利工程来说，可以简单概括为“挡水”与“输水”工程，处处都存在着流固耦合问题，例如坝坡稳定问题[2]、渗流问题[3]、水文问题[4]等等。近年来，沟道生态问题[5]愈发受到重视，本文主要针对排水沟道水流动力响应以及沟道边坡渗流稳定流固耦合问题的计算方法进行说明，对比各种计算方法的优缺点，为以后的研究进行前期准备工作。

1 流固耦合问题研究进展

1933年韦斯特加德[6]（H.M.Westergaard）等人着手研究了大坝的坝体与库水之间相互作用等一系列与耦合问题相近的接触问题[7]。20 世纪 30 年代，霍斯金斯（Hoskins）和雅各布森[8～10]（Jacobsen）等人对储液罐的力学性能进行了研究探讨。20世纪50年代，豪斯纳[11]（Housner）提出了基于刚性罐壁假设的质量弹簧系统简化模型。土力学方面，太沙基最早提出有效应力原理并提出了一维固结理论，比奥提出了真三维固结理论。以上两种理论是土力学流固耦合理论的基础。近年来，国外学者对流固耦合问题的研究更加深入更加多元化。

从20世纪70年代起，国内专家学者也对流固耦合问题进行了大量研究探索。东南大学的张海涛等对基于对自由液面的预测对非线性液体晃动进行了数值模拟[1]。河海大学赵兰浩[12]对坝体-库水动力相互作用进行了研究。华北水利水电大学付杰[13]对水体-结构-地基耦合作用进行了研究分析。

2 流固耦合问题计算方法

流固耦合问题的存在，使得流体介质与固体介质的相互作用问题变得复杂，涉及到诸多学科[14]，致使计算过程具有一定的难度。流固耦合问题研究目前大多是按照平衡和协调原则分别建立流体域、固体域以及交互作用面的控制方程[15]，求解得到耦合物理量。一般而言，控制方程有以下两点特征[16]:

（1）流体介质区域和固体介质区域均不能单独求解，否则肯定不满足耦合作用要求；

（2）不能随意改变或消去描述流体介质、固体介质运动的独立变量，变量之间相互依存、相互作用，是耦合作用的必需条件。

2.1 排水沟道水流动力响应计算方法

由于排水沟道内水流为非恒定流，水力学响应多采用圣维南方程组进行描述[17]。

（1）连续方程:

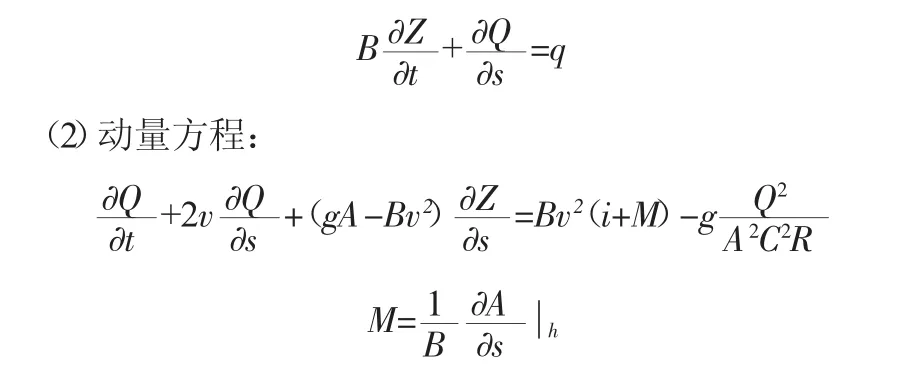
式中:B 为水面宽度，m；Z 为水位高度，m；t为时间，s；Q 为流量，m3/s；C为谢才系数；S为断面的距离坐标，m；q为区间入流量，m3/s；g 为重力加速度，m/s2；A 为过水断面面积，m2；v 为水流沿轴线方向的流速，m/s；R为水力半径，m；i为渠道底坡；M为明渠单宽、定深、断面沿程放宽率。

求解圣维南方程组的数值方法有普莱士曼(Preismann)隐式差分格式以及显示差分格式[18]，其中隐式差分格式具有精度高、无条件收敛等优点，显示差分格式计算用时较隐格式短很多，根据自己的需要进行合理的选择。

进行水力分析之后，往往需要进行水流对沟道边坡力学作用的分析，通常采用以下方法。

2.1.1 附加质量计算法

附加质量计算方法首先是由韦斯特加德（H.M.Westergaard）提出的。附加质量公式常用来模拟水的动力学效应。根据结构动水压力及附加质量法，计算固体变形时，排水沟道边界一侧单位面积水的附加质量可以采用下式计算[19]:

式中:Mw（z）为距离水面处的附加质量，kg；z为计算点到水面的距离，m；h 为结构内水的深度，m；ρ为水的密度，kg/m3；η 为折减系数。

利用这种方法进行附加质量的计算，忽略了水体的可压缩性，只是近似的处理方式，但由于计算简便，应用相当广泛。

2.1.2 豪斯纳（Housner）弹簧质量模型

豪斯纳（Housner）弹簧质量模型近似计算流体对固体产生的脉动压力和对流压力。可用固定于沟道边界的质量块来等效替代流体产生的脉动压力，使流固耦合问题的计算得到了简化[19]。

豪斯纳模型的优点是模型构造相对简单，避开了求解复杂方程的难点。此模型中流体是以集中质量的形式作用于边界条件上，所以运用此模型计算所得的边界条件内力和应力分布只是近似分布。

2.1.3 边界元法

边界元法是从边界条件出发，仅仅把流体的自由表面及交互作用边界作为研究对象，将水体所满足的二维拉普拉斯方程进行离散，转化为边界积分方程，采用时间增量法求解积分方程[19]。

运用边界元法解决流固耦合问题，可以得到液体晃动的波高和速度势的分布情况。此方法仅仅反映了流体对固体的影响，并未反映固体变形对流体的影响。

2.1.4 ALE有限元法

ALE（Arbitrary Lagrange-Euler）最初用于数值模拟流体动力学问题，后来引入到流固耦合问题研究中[20]。1974年，赫特（Hirt）等人提出了任意的Lagrange-Euler方法，简称ALE法。将拉格朗日（Lagrange）坐标和欧拉（Euler）坐标结合起来，可以在交界面处采用纯拉格朗日表达，同时可以保证在大变形时，网格不至于过大的扭曲。

ALE有限元法已被广泛应用于解决流固耦合问题，ALE有限元算法对网格的运动计算方法有较高的要求，计算较为复杂。王跃先[21]、岳宝增[22]、蒋莉[23]等人对此方法都进行了研究探讨。

2.2 排水沟道边坡稳定问题

边坡稳定问题的研究已有悠久的历史，但是对于排水沟道小型边坡的稳定分析研究相对来说较少。采用数值分析方法对边坡进行稳定分析已经成为近来研究的热点，耦合理论也广泛应用于边坡稳定分析，对耦合分析方法进行简单的描述。

2.2.1 条分法与有限元耦合（LE-FEM）分析法

条分法引入假定条件较多，不能反映边坡实际应力状态。有限元分析法克服条分法的不足，在分析过程中避免了太多的假定条件。将条分法与有限元法进行耦合，采用有限元分析获得边坡整体的真实应力场，然后利用极限平衡理论求解安全系数。

边坡稳定性的条分法与有限元法耦合分析的基本原理及分析步骤是[24]:

（1）利用有限元分析法，获得边坡的整体应力场；

（2）将边坡滑移体进行条分，获得条块计算参数；

（3）计算所分条块底面中心处的各项应力；

（4）计算整体稳定安全系数。

2.2.2 渗流场与应力场耦合分析法

渗流场改变，应力场随之变化，致使边坡土体产生压缩变形，土体孔隙率改变，渗透系数发生变化，最终导致整个渗流场的变化。渗流场与应力场这种耦合关系对边坡稳定性具有非常大的影响。

学者对边坡渗流稳定问题进行了深入的研究，沈珠江[25]进行了比奥固结方程的有限元法求解；毛昶熙[26]等以渗透力的形式考虑渗流对边坡稳定的影响，提出了考虑渗流作用的边坡稳定极限平衡计算方法；李培超[27]等对饱和多孔介质渗流应力和孔隙压力耦合作用的数学模型进行描述；师文豪[28]等基于等效连续介质模型和Louis经验公式，建立了层状边坡各向异性岩体渗流-应力耦合模型，应用COMSOL多物理场耦合软件对模型进行了数值计算。

渗流场与应力场耦合分析法通过基于不同的理论方法与数学模型，建立渗流场与应力场平衡的控制方程，根据不同的实际需求，采用相应的求解方法进行计算。求出渗流曲线，使用不同的方法对边坡的渗流稳定进行分析，大多使用强度折减法。

2.3 沟道边坡在水流冲刷和边坡渗流双重作用下的稳定分析

排水沟道边坡稳定是依靠边坡抗冲刷力与水流冲刷力相互作用的结果[29]。水流冲刷力与沟道边坡在渗透力作用下的抗冲能力相互消长。河流冲刷天然土质沟道边坡，使边坡变陡、坡高增加，结果造成边坡坍塌。对于衬砌边坡，水流冲刷坡脚，坡脚的几何形状发生变化，又反过来影响河势，河势的变化再作用于边坡，堤脚受到进一步影响，使边坡稳定性降低，减少排水沟道使用期限。

目前研究水流冲刷与渗流相互作用影响沟道边坡稳定的热点问题主要有:（1）沟道边坡所受冲刷力的分布和抗冲刷力计算模式的研究；（2）沟道边坡土体横向冲刷量的计算方法研究；（3）在已知冲刷量的基础上，采用极限平衡方法判断沟道边坡的稳定性，提出了诸多计算模型，改进后的模型见图1，考虑了静水压力和孔隙水压力的作用等。张芳枝[30]在流固耦合分析基础上，建立了多项耦合力系下的堤岸与河床整体分析模型，分析河流冲刷作用对堤岸渗流的影响，并结合极限平衡法，探讨河流冲刷对堤岸整体稳定性的影响。对于排水沟道边坡在水流冲刷和边坡渗流双重作用下的稳定分析，也可以借鉴类似的分析计算方法，建立整体三维模型，采用有限元模拟方法对沟道边坡稳定进行计算分析。

图1 改进后稳定分析示意图

3 结论

本文对考虑流固耦合的排水沟道力学问题的研究进展以及计算方法作了概要的梳理，计算方法各有特点。

沟道内部水流力学特性计算方法:

（1）附加质量法，计算简单方便，计算量较小，但是忽略了流体晃动对控制边界的不利影响；

（2）Housner弹簧模型，模型概念简单，但是分布力简化为集中力，计算结果较粗糙；

（3）边界元法，考虑了液体晃动的影响，但是只能算是单向耦合，忽略了结构对流体的作用；

（4）ALE有限元法，适用于求解流体问题，但是计算比较复杂。

排水沟道边坡稳定分析计算方法:

（1）条分法与有限元耦合（LE-FEM）分析法，将传统的极限平衡条分法跟有限元计算联系起来，结果更加精确，但是没有考虑渗流对边坡稳定的影响；

（2）渗流场与应力场耦合分析法，充分考虑了渗流与应力之间的耦合关系，进一步求解安全稳定系数，计算结果较为理想。

沟道边坡在水流冲刷和边坡渗流双重作用下稳定计算多采用简化模型计算，改进后的模型相对精确，但是并没有充分考虑渗流对边坡稳定的作用。在计算过程中均采用二维模型，但是实际问题多为三维状况，与实际不相符。

考虑流固耦合的排水沟道力学问题研究有重大的实际意义，但是目前研究相对较少，特别是考虑沟道内部水流冲刷与外侧土体渗流双重作用的边坡稳定问题。随着流固耦合问题研究的不断深入，对于排水沟道力学问题的研究必将更加全面。