高温作业专用服装的多层非稳态热传递模型的研究

方志法 李浩铭 王文昊

摘要：文章通过建立数学模型对三层织物材料组成的专业服装进行研究，建立起了多层非稳态热传导模型，并推导出了各层的分析解。文章基于热传导方程及傅里叶定律、牛顿冷却定律，从一层到多层的递推思路，得到各层的热传导方程组，利用分离变量法和乘积解法，推导出二维坐标下温度分布的导热微分方程。最后用ANSYS的有限元分析工具模拟问题的具体情形，对模型的正确性进行验证。

Abstract： This paper establishes a mathematical model to study the professional clothing consisting of three layers of fabric materials， and establishes a model of multi-layers unsteady heat conduction， and derives the analytical solutions of each layer. Based on the heat conduction equation， Fourier's law and Newton's cooling law， the heat conduction equations of different layers are obtained from one layer to many layers. The heat conduction differential equation of temperature distribution in two-dimensional coordinates is deduced by using the method of separation of variables and the method of product solution. Finally， the ANSYS finite element analysis tool is used to simulate the specific situation of the problem and verify the correctness of the model.

关键词：热传导;高温作业专用服装;有限元;数学模型

Key words： thermal conduction;thermal protective clothing;finite element analysis;mathematical model

中图分类号：O482.2+2                                  文献标识码：A                                  文章编号：1006-4311（2019）18-0260-03

1  绪论

1.1 选题背景

“高温工作”是基于穿着热防护服装的长时间处于高气温、气湿、热辐射下的异常工作，因而起到应急防护功能的专业服装尤为重要，其材料必须具有良好的隔热，阻燃特性，使得高温工作者能安全舒适、高效率的从事活动。

在热发电厂、消防、石油化工等行业工作的工作人员都需要具备长时间在高温以及强热辐射的环境下作业的能力。若高温作业人员在作业时未能做好高温防护措施，则会出现多种热失调的临床现象，典型症状有头昏、口渴、全身乏力、注意力不集中等，严重危害人的生命安全。[1]为了保证在此极端环境下工作人员的安全，高温作业防护服成为了必不可少的防护装备。

近年来，经济、安全、有效的高温作业专用服装逐渐成为人们研究的热点。高温防护服的主要功能是阻挡外界热量以达到保护高温工作者免受伤害的目的。[2]本文，我们通过建立三层织物构成的热防护服的热传递模型，准确预测人体皮肤外侧温度变化，缩短研究开发周期，减少实验投入，为后人研究高效经济的热防护服奠定基础。

1.2 问题提出

我们将构成高温作业专用服装的三层织物，从外向里分别记为I、II、III层。其中第一层与外界环境接触，而第III层与皮肤之间存在空隙，将此空隙记为第IV层。

而后我们需要根据传热的基本规律，在将假人合理地简化为规则几何体的情况下，建立起准确的数学模型，推导出假人皮肤外侧的温度在不同外界温度，不同层厚度和不同传热时间下的变化的基本规律。

2  基本假设及符号定义

2.1 基本假设

①面料的热物理参数、对流传热系数、面料厚度等均为常量，不考虑纤维热分解反应的影响。②该模型仅考虑热传递，包括热辐射、热传导及外界环境的热对流现象，空气层不考虑热对流。③热防护服的织物视为各向同性。④热传导和辐射热传递到织物的过程是均匀的。⑤人体热辐射极小，对模型的温度分布影响忽略不计。

2.2 定义符号

本文中用到的主要符号参照表1。

3  多层非稳态热传导模型的建立与求解

3.1 概述

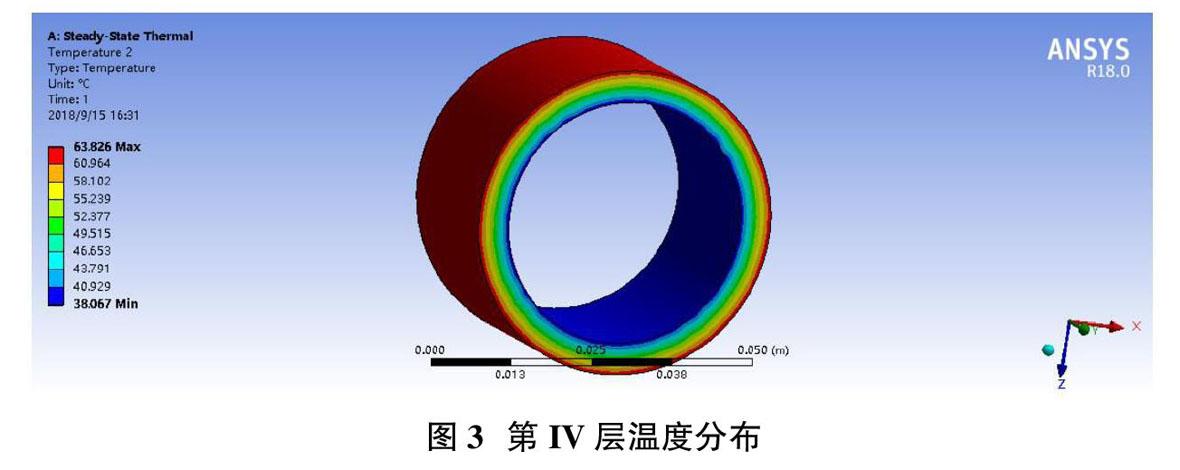
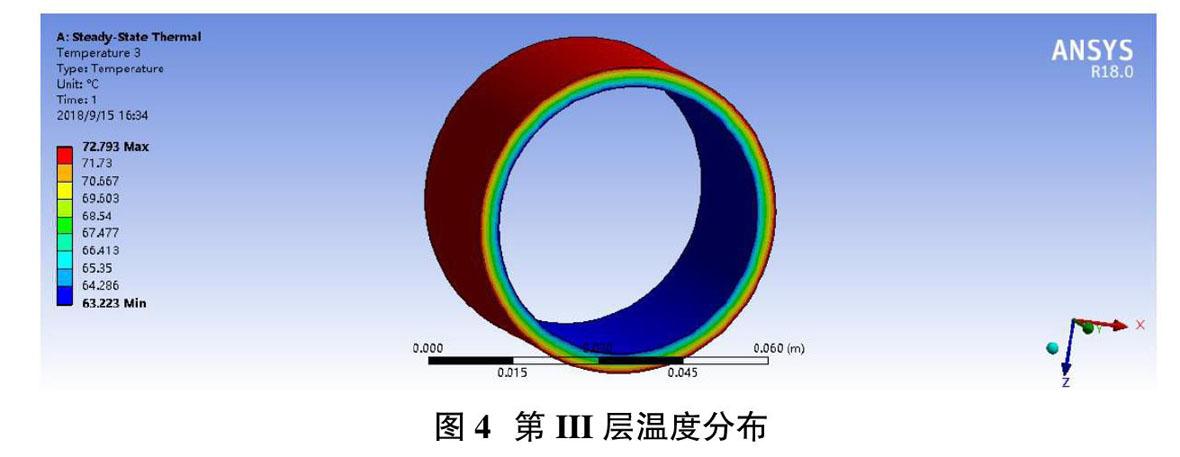
首先，我们建立能够计算温度分布的模型，因为人的形状是较为复杂的，将导致每个时间点、每一点处的传热情况不尽相同，所以我们认为此模型应该建立在高维坐标下，不单单研究半径方向的温度分布。为了便于研究，我们将研究对象看作为由三层圆筒包裹的圆柱体，由于圆柱体内温度沿半径对称分布，且在三维u（x，y，z，t）坐标系下的热传导方程求解过于复杂，我们将其转化为（x，z）坐标的二维非稳态热传导问题。考虑到多层迭代，我们从简单的一层入手，根据二维坐标下的热传导方程，以及初值条件，邊界条件，我们推导出导热微分方程，结合傅里叶定律和牛顿冷却定律，我们得到I层与II层交界处的温度分布，以其作为II层的“热源”继续研究推导出III层间的温度分布，依次同理得出每个时间点各层的温度分布，至此问题初步解决。最后通过ANSYS有限元分析软件，模拟在题目给定各层织物材料属性的条件下进行热传导至稳态的过程，得到接近实际的稳态温度分布图来检验模型的正确性。