基于模糊动态故障树的动车制动系统可靠性分析
郭济鸣 齐金平 李兴运
1.兰州交通大学机电技术研究所,兰州,7300702.甘肃省物流及运输装备信息化工程技术研究中心,兰州,730070
0 引言
制动是动车组最为关键的工况之一,有效的制动性能及其工作状态直接影响车辆的运行安全性、可靠性等一系列重要性能。在实际工作环境中,制动控制系统各个环节组成部分不是简单地服从某种规律,而是相互间存在着顺序相关性、功能相关性和优先性等动态特点,而且非精确统计和主观原因等不确定性成分会造成对系统零部件实际状态的误判,致使得到的基本事件故障率不够精确,根据实际工况所建立的系统模型都比较复杂且存在失效数据严重缺乏的问题。
周笛等[1]根据系统动态响应反馈,结合系统的运动、结构、材料等参数的随机性,分析得出了系统的动态可靠性。王华伟等[2]针对每种失效状态分别进行可靠性建模,利用BMA(block matching algorithm)研究了各动态失效状态对航空发动机可靠性的影响。但是以上研究未考虑事件故障率的模糊不确定性。CHEN等[3]应用三角模糊数和高斯模糊数预测方法,对工业液压系统进行了可靠性评估。IZABELA等[4]提出了基于模糊理论和模糊集的专家对危险管道失效程度进行评估的供水管网技术状况评价方法。SEYED等[5]提出了一种结合模糊故障树处理数据短缺的风险评估方法。刘英等[6]针对系统中各部件故障率的不确定性问题,应用模糊数学理论,将事件概率模糊化,得到了可靠性指标。以上研究没有对系统故障动态特点进行分析,也没有对系统故障率的发生进行预测。
基于以上研究,本文借助专家信心指数法和三角模糊数,通过扩展原理得出制动控制系统各基本事件发生的模糊率,运用马尔可夫模型结合故障树模型对制动系统进行动态故障树构建,通过对所建立的模型进行分析得出系统的马尔可夫状态转移图,从而得出了动车制动系统故障的模糊失效概率函数,计算得出了制动系统的失效概率,进而得到了系统预测可靠度曲线。
1 故障数据的处理
系统故障可靠性分析中的数据处理往往不能得到一个确定准确的事件故障率[7],因此应用模糊集理论和扩展原理进行模糊处理,得到事件故障率的模糊区间,使得到的数据更加符合实际故障率特性。
1.1 模糊集
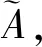
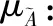
根据典型的三角模糊数定义,得到它的隶属函数如下[8]:
(1)
典型的三角模糊数隶属函数如图1所示。
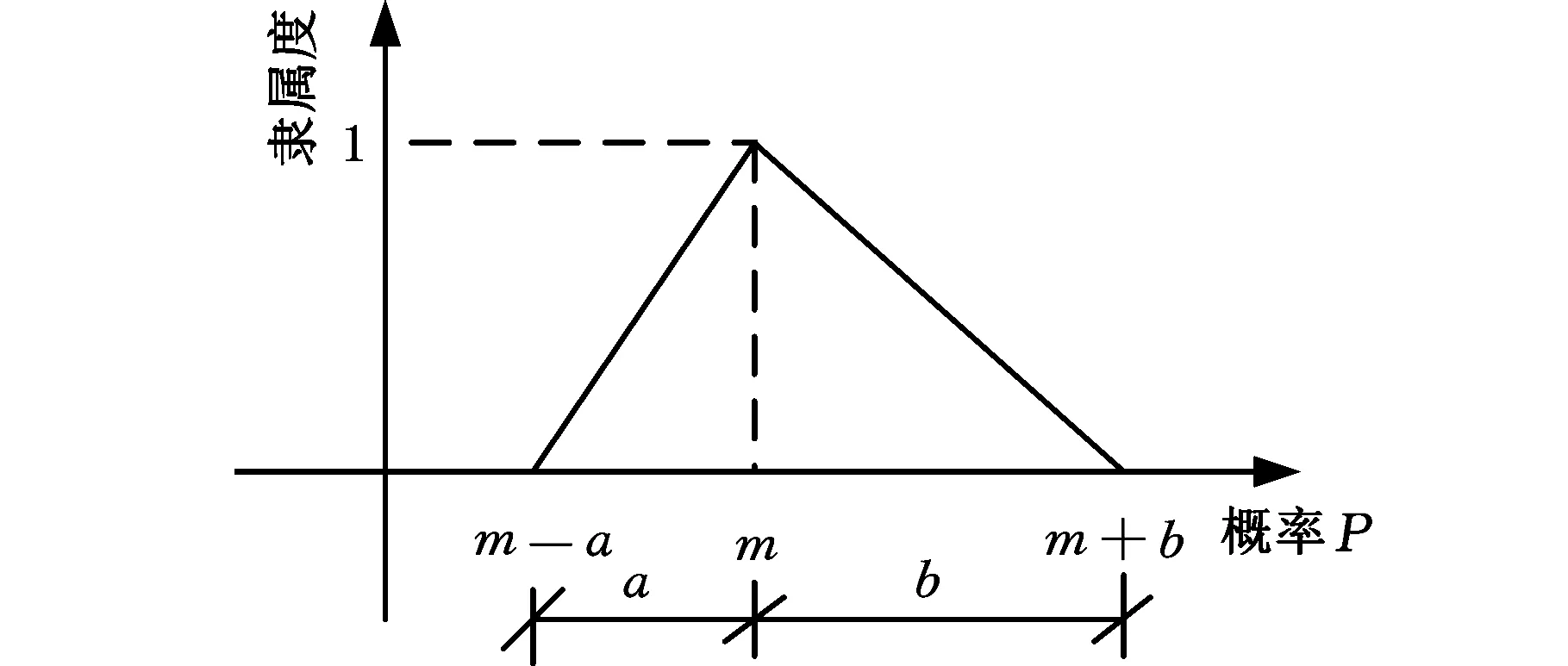
图1 三角模糊数的隶属函数Fig.1 The membership function of trigonometric fuzzy numbers
1.2 扩展原理
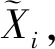
(2)
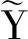
(3)
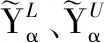
(4)
s.t.
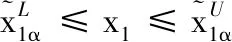
(5)
s.t.
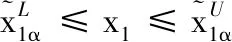
根据以上扩展原理可得到模糊数在不同截集下的区间边界。
2 动态故障树分析方法
动态故障树在马尔可夫链的基础上,结合了静态故障树的优点,既能简单方便地表示出整个系统中存在的静态逻辑关系,同时也可以描述各个动态转移过程[9-10]。动态故障树首先根据系统中各部分的相互逻辑关系来构造,然后分析出各个静态子树、动态子树等,简化之后对整个系统进行马尔可夫状态描述,从而分析出最后结果。设定系统部件失效符合指数分布且为不可修复产品。
为研究解决系统在可靠性建模和分析中的动态特征及模糊不确定性问题,结合马尔可夫模型与模糊集合理论,得到了可以应用于含有动态失效特性和模糊不确定性的系统的可靠性分析方法中。应用此模型进行分析时,首先分析系统的失效原理,进而构建系统的动态故障树,然后通过马尔可夫模型将含有n个状态的动态故障树进行转化,将不同状态间的相互转移率以模糊数形式表达,进而将模型的状态转移率矩阵转化成模糊状态转移率矩阵,具体形式如下:
(6)
模糊状态转移过程如图2所示。图2中,S1表示系统正常的运行状态,Si(i=2,3,…,n-1)表示系统出现发生故障的零部件但不影响系统正常工作的中间状态,Sn表示系统处于失效状态。
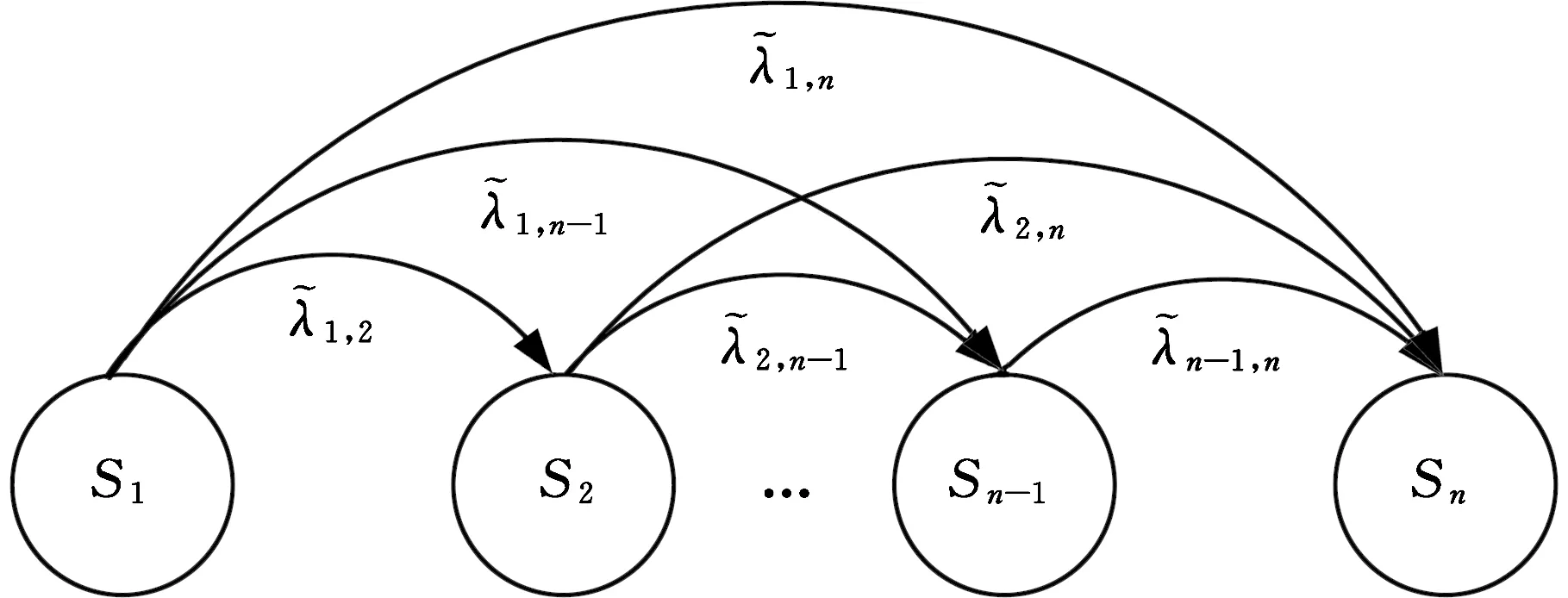
图2 无法修复的系统模糊状态转移图Fig.2 Fuzzy state transition diagram of a system that can not be repaired
模糊马尔可夫模型的微分方程形式如下:
(7)
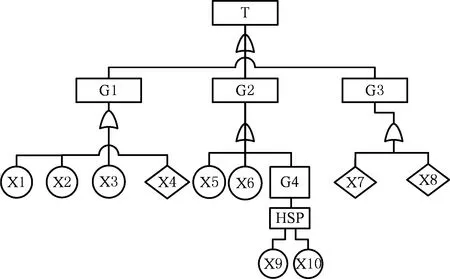
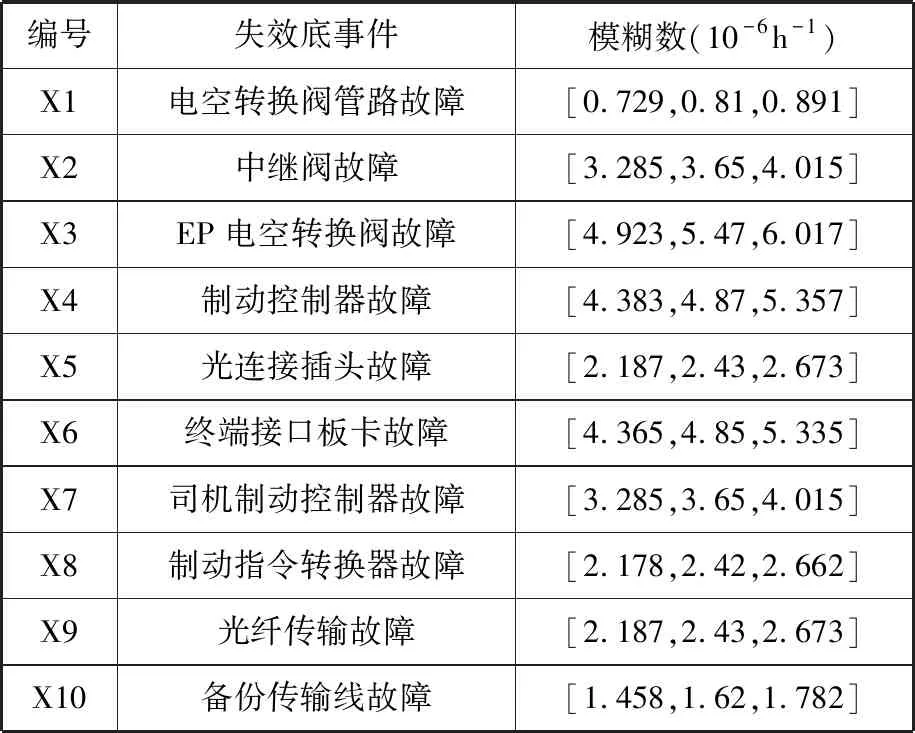
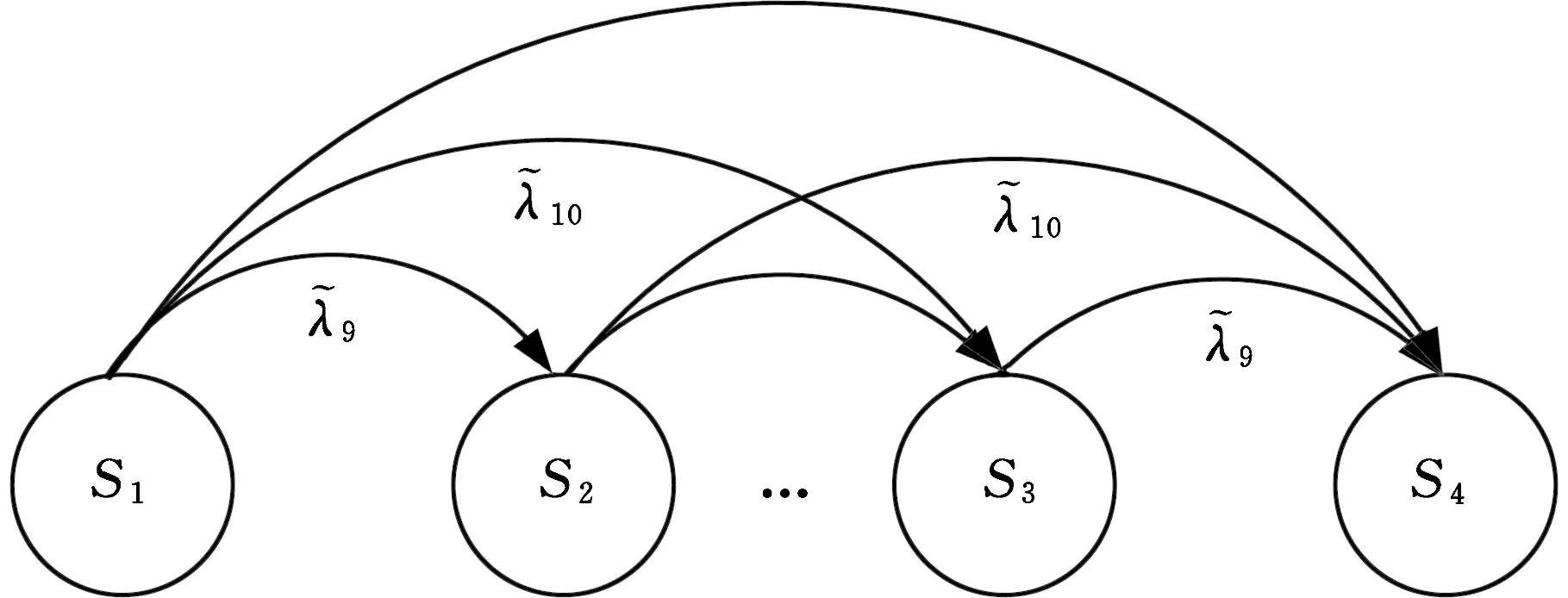
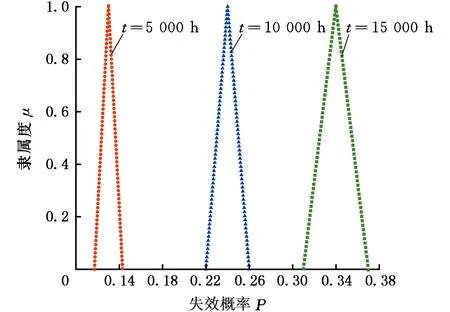
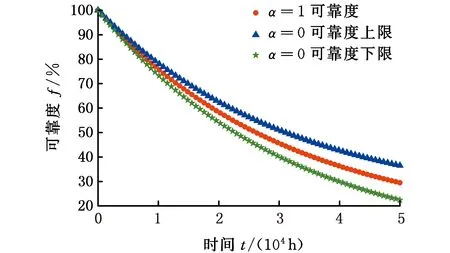
1 (8) 1 制动系统是影响动车组安全工作的重要部件之一,伴随动车组行驶速度的不断提高,对列车制动性能的要求也随之提高,在保证车辆正常运行的前提下,需要确保动车组可以高效而安全地制动,一旦某一环节出现问题而制动失效将危及整个车辆的运行安全。因此制动系统的可靠度极其关键,有必要对其进行可靠性预测,以预测并避免制动系统潜在的安全隐患。本文以兰新线CRH5动车组的空气制动控制系统为例进行分析。 制动控制系统工作原理如下:司机制动控制装置生成电气信号,通过信息控制装置输送给其他车辆的制动控制装置,电子制动控制单元发出制动指令,分析出要提供的空气制动力大小,然后通过传递电信号来对空气制动控制单元进行控制,空气制动控制单元中的电空转换阀收到来自于电子制动控制单元的电信号后将其转换为相对应的预控压力信号到中继阀,最后通过中继阀的流量放大将压缩空气送至增压缸,进而形成空气制动力来完成制动作用。 建立故障树,选定制动控制系统故障为顶事件,且各子系统的工作状态影响着整个制动控制系统的运作,即任意子系统出现问题就会造成动车制动控制系统无法正常工作[11]。制动控制系统可视为由制动控制装置、制动信号传输装置和制动信号发生装置3个子系统串联共同组成,3个子系统为中间事件。所创建的故障树如图3所示。 图3 制动控制系统动态故障树Fig.3 Dynamic fault tree of brake control system 应用模糊数学理论,结合专家调查问卷对兰新线路上制动控制系统运行的全部风险事件故障数据进行整理分析[12-13],获得基本事件故障率,表1给出了用三角模糊数计算得到的风险事件故障率及故障树中各底事件编号所匹配的故障名称。 表1 底事件名称对应的编号及故障率Tab.1 The number and failure rate corresponding to the name of the bottom event 根据2.1节对图3所构建的模型进行分析,图 4所示即为将故障树模型向模糊马尔可夫模型转化的过程。其中,S1表示制动控制系统正常工作状态,S2表示光纤传输故障,S3表示备份传输线故障,S4表示制动控制系统故障。模糊状态转移率矩阵根据每个基本事件的模糊失效概率和状态转移图得出,形式如下: (9) 图4 模糊状态转移图Fig.4 Fuzzy state transfer graph 由此得到状态转移图所对应的微分方程为 (10) t≥0 (11) 求解线性方程组得 (12) 为获得制动控制系统在失效状态的概率关于时间t的函数,对式(12)作Laplace-Stieltjes逆变换,得到面板的模糊失效概率函数为 (13) 根据模糊集合的扩展原理中相关公式,在给定时间t前提下,可推导出制动控制系统在失效状态S4的模糊概率在不同截集下的上下限,得出制动控制系统在时刻t时的模糊失效概率的隶属函数。 系统运行时长t分别为5 000 h、 10 000 h、15 000h时失效模糊概率的隶属函数如图5所示。模糊概率的中值分别为0.130 1、 0.241 0和0.335 6,此数值代表制动控制系统运作时长达到t时失效概率的最大可能值。 图5 模糊故障率隶属函数图Fig.5 Fuzzy fault rate membership function diagram 在固定水平截集下,得出预测的系统可靠度如图6所示。 图6 水平截集α=0及α=1时的系统模糊可靠度Fig.6 System fuzzy reliability of horizontal intercepting α =0 and α =1 (1)将模糊数学和马尔可夫模型与故障树模型相结合提出了一种基于模糊马尔可夫模型的动态故障树分析方法,解决了不确定条件下动态系统可靠性分析问题。 (2)根据对兰新高速铁路线上的CRH5型动车制动控制系统的分析,得出了制动系统的故障发生率和可靠度,为制定该线路上运行车辆的检修策略提供了理论依据。 本文方法虽然在故障分析时提高了算法的准确性,但由于数据不充分或者不准确, 在分析过程中仍存在人为误差,为了保证结果更加准确, 有待于今后数据的积累。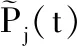

3 案例分析
3.1 动态故障树建模
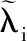
4 结论

