多维复杂关联因素下的大坝变形动态建模与预测分析
李明超,任秋兵,孔 锐,杜胜利,司 文
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300354;2. 中国电建集团西北勘测设计研究院有限公司,陕西西安 710065)
1 研究背景
我国大坝建设取得了举世瞩目的成就,目前已有三峡、锦屏等一批大型水电工程[1-2]。大坝数量急剧上升,大坝溃决造成的损失亦随之增加,这将加强大坝安全管理摆到了更为重要的位置。大坝安全监测是大坝安全管理的重要内容,同时是掌握大坝运行性态的主要手段[3-4]。鉴于此,对安全监测资料进行综合分析是评判大坝安全状况的最直接有效的方法之一。其中,大坝变形观测资料易于获取,能直观可靠地反映大坝服役性态,故常运用数学模型和坝工理论构建大坝变形监控模型[5]。建立可靠的大坝变形监控模型对于及时发现安全隐患、保障大坝稳定运行具有重要意义。
大坝与基岩有机构成一个复杂时变的动力系统,其变形、渗流等效应量(又称响应变量)自身具有不确定性、高度非线性等特征[6-7]。在系统内部,各变形监控点观测数据序列之间往往存在交叉相似性,尤其是同一坝段不同高程的变形数列。此外,大坝在服役期间始终受到降水、库水位、坝址气温等外部环境因子(又称解释变量)的耦合作用,即具有多诱因性[8-9]。因子间亦存在显著的交互效应(简称因子相关性),例如库区降水量、气温势必会影响上下游水位变幅,进而引起变形性态的变化。就整体而言,关于大坝变形的复杂关联性主要体现在单一因子内部、多因子之间、变形与因子之间、单一变形数列内部以及多测点变形数列之间等5个维度上。需要说明的是,单一环境因子内部的关联性并不属于大坝安全监控研究的范畴,至于单一变形数列内部的关联性,可参考文献[10]。因此,本文将重点对多因子之间、变形与因子之间以及多测点变形数列之间的关联性在大坝变形动态建模中的应用展开研究。
大坝变形监控模型是多维复杂关联性以数学形式表达的集成载体。目前,国内外常用的数学建模方法主要包括数理统计法、时序分析法和因果建模法等[11-12]。因果建模法由于适合处理复杂输入-输出关系且能够整合多元监测信息,现已成为应用最广泛的大坝变形数学建模方法。该方法一般根据历史监测资料找出响应变量与其解释变量之间的因果关系来建立相应的数学模型,然后通过求解对效应量作出估计[13-14]。例如,张豪等[15]根据各因子的特性,利用经验模态分解和支持向量机(sup⁃port vector machine,SVM)构建出多尺度大坝变形监控模型。Kang等[16]提出了一种基于极限学习机的混凝土坝变形监控模型,并通过实例证明了该模型的有效性。Su等[17]采用相空间重构、改进粒子群优化小波支持向量机等算法建立了大坝变形组合预报模型,并将其应用于实际工程。总而言之,大坝变形与环境因子间的因果关系是构建上述模型的基础。然而,多数因果模型赋予不同因子的输入权重几乎一致[18],实则各因子对于大坝变形的影响程度是不同的,并且会随着时间的推移而不断变化。Dai等[19]借助统计模型优化随机森林的方法证实了这一观点,但其仍着重于静态差别,而未顾及到因果关系的动态演化过程。
大坝变形数学建模仅考虑动态因果关系是不够的。因子相关性会对模型的准确性和稳定性产生影响,特别是统计模型[20]。尽管运用简单剔除[21](如逐步回归)、合并降维[22](如主成分分析)等方法可以减小其影响,但仍未从根本上解决该问题。从模型角度考虑,以SVM 为代表的非线性模型(如随机森林等)不易受因子相关性的影响[23],进一步体现出非线性因果建模的优越性。此外,监测信息利用不充分,比如忽略多测点变形数列之间的相似性,会导致多测点监控模型的泛化能力不足。文献调研发现,目前国内外有关多测点变形数列相似性的研究相对较少,已有研究多集中于插值填补[24]、异常检测[25]等方面,这足以说明直接将序列相似性应用于数学建模尚未引起学术界的广泛关注。于是,本文将因子相关性和序列相似性纳入到大坝变形动态监控模型之中。
综上,本文拟开展综合考虑动态因果关系、因子相关性以及序列相似性等多维关联性影响下的大坝变形动态建模及应用研究,其主要包括以下几个方面的内容:(1)传统因果建模中,各环境因子与大坝变形间的因果关系多用静态线性相关系数来量化,难以体现两者间的动态非线性演化过程。为真实反映因果关系,特提出一种动态非线性因果关系检验方法(dynamic nonlinear causality test,DNCT);(2)针对如何衡量多测点变形数列间的相似性以及如何将其应用于大坝变形数学建模等问题,分别提出标准化动态时间规整算法(normalized dynamic time warping,NDTW)和交叉多输出模型改进措施;(3)为验证考虑因子相关性的必要性,引入一种耦合方差扩大因子(variance inflation fac⁃tor,VIF)和条件数(condition index,CI)的相关性诊断方法(VIF and CI-based coupling collinearity test,VCCT);(4)结合工程实例,就如何将上述复杂关联性集成于同一大坝变形数学模型中这一难题,总结提出一种兼顾相关性和相似性的大坝变形动态监控模型(causal model combining correlation with similarity,CMCS),并将其与传统常用模型进行对比。
2 总体框架
根据环境因子及多测点变形数列等监控资料,在充分考虑动态因果关系、因子相关性以及序列相似性等多维关联性影响的前提下构建大坝变形动态监控模型(CMCS),并将该模型应用于实际工程,研究框架如图1所示。
(1)在维度层面上,建立因子集是探讨多维复杂关联性的基础,遂以坝工理论和数理统计方法为依据对环境因子进行合理筛选。
(2)在关联层面上,将多维关联性细分为动态因果关系、因子相关性以及序列相似性等3 个维度,从而降低数学建模的复杂度。
(3)在检验层面上,为全面验证考虑多维复杂关联性的必要性,从上述3个维度出发提出对应关联性的检验方法。
(4)在措施层面上,本文着重研究3种关联性并存的最复杂情况,为此分别提出相应的数学建模方法。
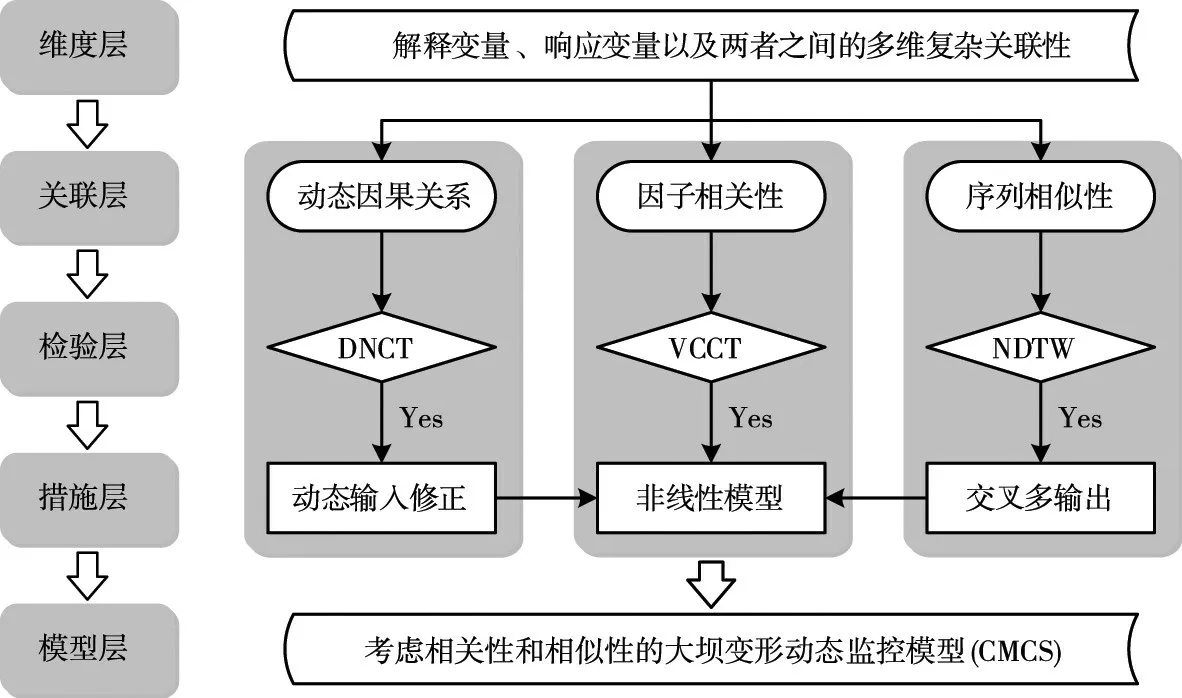
图1 大坝变形动态监控模型总体框架
(5)在模型层面上,将多种建模方法集成在同一模型中,随即得到考虑相关性和相似性的大坝变形动态监控模型。
(6)以某混凝土重力坝为例,先构建各坝段的变形监测数据库,后将所提模型应用于该项工程,并通过对比分析来验证所提模型的有效性和准确性。
3 多维复杂关联性检验及动态建模方法
3.1 多因子相关性大坝变形除受库水压力(水压)影响外,还受到温度、渗流以及时效等因素的影响,其中水压由上游来水量、库水位、库水比重等因素确定,温度由季节变化、气象条件等因素确定,上述因子影响层级呈现树状结构[26]。鉴于此,从众多影响因子中提炼出少量能够反映大坝变形信息的因子就成为大坝变形数学建模的关键。目前发展较成熟且应用较多的变形监控模型主要有统计模型和确定性模型。与确定性模型相比,统计模型拟合精度较高,尽管没有考虑大坝及坝基的物理特性,但已囊括大部分环境和结构信息,因而可据其建立因子集。具体来说,大坝变形δ按其成因可分为水压分量δH、温度分量δT和时效分量δθ,仅有气温资料时,变形统计模型[3]可表示为:
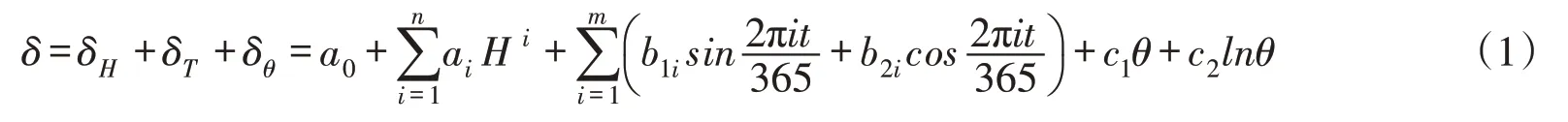
式中:a0为常数项;H 为上游水深;n为坝型系数,对于不同坝型,n 取值不同,其中重力坝一般取3,拱坝宜取4或5;i 为周期,对于年周期i=1,对于半年周期i=2;t 为监测日到基准日的累计监测天数,其中θ=t 100;m 通常取1或2;ai、b1i、b2i、c1和c2均为未知系数。

式中:VIFi为自变量xi的方差扩大因子;CIj为特征根λj的条件数;Ri2为自变量xi对其余p-1个自变量的复决定系数; λm为矩阵XTX 的最大特征根[27],X 为自变量构成的矩阵。通常,当VIFi≥10 且CIj≥100 时,认为各因子间存在较为严重的相关性。
一般统计模型不适合处理因子相关性问题。此外,构建统计模型需要大量监测数据,其预测效果亦不理想。机器学习建模方法现已成功应用于大坝变形性态分析,尤以神经网络和支持向量机(SVM)为甚。其中,SVM在解决小样本、非线性及高维数问题中表现突出,并且不易受到因子相关性的影响,因而本文将基于SVM进行大坝变形动态建模。SVM模型基本原理和具体计算方法详见文献[28]。
3.2 动态因果关系作为一种输入-输出模型,SVM 常用来反映环境因子与大坝变形间的因果关系,但其在应用中仍存在固有问题,即模型对各个归一化输入因子的精度要求以及偏离精度要求的惩罚是一视同仁的[29]。实际上,不同环境因子对变形产生的影响往往有所不同,故需将这种“区别对待”引入模型中。诸多学者对此开展了广泛研究,其中利用静态线性相关系数(如Pearson 相关系数[30]、统计模型回归系数[19]等)对不同因子分别进行加权处理是最常用的方法。该方法在一定程度上解决了这一问题,但用一定值量化因子与变形间的长期因果关系显然是不合理的。大坝服役性态并非是一成不变的,水位、气温等环境因子在其运行中也是不断改变的,据此断定因子与变形间的因果关系始终处于动态变化中,且属于非线性关联。因此,有必要采用一种动态非线性方法对模型输入进行适当修正。
滚动时间窗口算法[31](rolling time window,RTW)是一种动态序列分析技术,可直接反映因子对变形所施加作用的动态特性。最大信息系数[32](maximal information coefficient,MIC)不仅可以度量两变量间的线性和非线性关系,还可以探索两者潜在关联性,如函数叠加等。为此,整合RTW和MIC提出一种动态非线性因果关系检验方法(DNCT),进而实现对SVM模型的动态输入修正。现给定因子集{A1,A2,…,Am,…,AM}和多测点变形数列集合{B1,B2,…,Bn,…,BN},分别选定因子和变形数列作为初始解释变量和响应变量,那么DNCT具体实现过程如下:
(1)步骤1。全部输入因子Am(m=1,2,…,M )均作同维规范化处理,以消除各个因子量级不同所带来的影响[33]。此外,从A1、B1开始,根据监测数据量k 分别设置其滚动窗口大小为ωAm和ωBn(ω=ωAm=ωBn)。
(2)步骤2。在同一时间窗口内,给定有序对组成的有限集合对Am、Bn构成的散点图中不同区域G进行x列y行网格化(允许某些网格为空集),并通过概率质量函数D|G 求出所有网格G在D上的最大互信息值MI*(D,x,y ),即:

(3)步骤3。对集合D上不同网格G的所有最大互信息值进行归一化,得到特征矩阵M( D )x,y:

(4)步骤4。通过穷举搜索获取特征矩阵中的最大归一化互信息值,也就是最大信息系数MIC( D ),0 ≤MIC( D )≤1。值得一提的是, MIC( D )不受解释变量(即Am,m=1,2,…,M )间显式函数关系的影响。
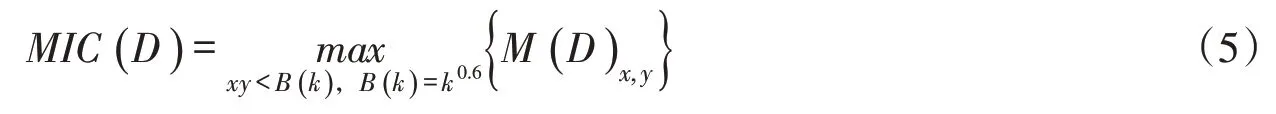
(5)步骤5。利用嵌套循环计算全部环境因子Am(m=1,2,…,M )与多测点变形数列Bn(n=1,2,…,N )的动态最大信息系数DMICim×n(i=1,2,…,k ),其中循环次数C 由因子数量M和测点个数N确定。
(6)步骤6。将因子序列中各个时间点的监测量(或派生量)aim乘以对应动态最大信息系数以获得动态修正后的输入因子集{A′m,m=1,2,…,M }。
3.3 多测点相似性多测点变形数列间的相似性目前在大坝变形建模中的应用相对较少,本文将对此进行初步探讨。一方面,不同于动态因果关系,序列相似性一般较为稳定,故可用一定值来量化。另一方面,仅用定值表示变形数列相似性,并将其与SVM相衔接,显然未考虑多测点变形数列间的交叉(即一对多)关系。为此,分别提出标准化动态时间规整算法(NDTW)和交叉多输出改进措施。动态时间规整算法[34](DTW)是一种衡量时间序列相似度的经典方法,常用于语音识别、手势辨认和信息检索等领域。然而,在利用DTW 度量变形数列相似性时,尺度不一(如某测点变形δ <10 mm ,而另一测点变形δ′>20 mm)致使难以对度量结果进行横向比较,遂先利用标准化将各因子数值限定于既定范围(0,1),后采用DTW度量其相似性,其求解步骤详见文献[5]。另外,鉴于序列相似性存在交叉关系,多测点变形数列必须同时进行外推预测方能顾及响应变量间的关联性,特将SVM由独立单输出改进为交叉多输出模式,主要改进如下所述。
本文引入一种分层贝叶斯方法[35-36],将多测点变形数列间的交叉相似性集成于常规SVM中,以改善因子集A ∈ℝM到多测点变形量B ∈ ℝN的映射关系。与常规SVM 相仿,通过求解权函数和偏差向量即可完成数学建模。现假设wi=w0+vi,wi∈ ℝnh,i ∈ ℕN,其中vi∈ ℝnh承载“相似信息”,序列相似性愈高,vi值愈小;反之,则承载“共性信息”的平均向量w0∈ ℝnh值愈小。据此,最小化下列带有约束条件的目标函数,如式(6)所示,以同时解得w0、b 和
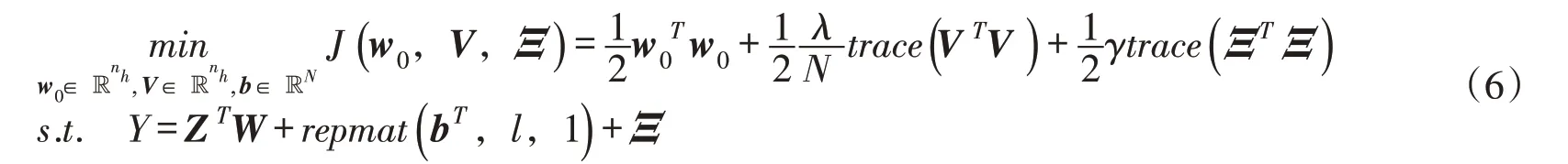
式中:Ξ 为松弛变量;Z 为将输入因子集A ∈ℝM映射到nh维希尔伯特空间(即特征空间)的函数;W=(w0+v1,w0+v2,…,w0+vN)∈ℝnh×N;γ、λ ∈ℝ+均为正则化参数。
通过构造拉格朗日函数,结合Karush-Kuhn-Tucher 条件,简化得到下列等价优化问题,其约束条件仅涉及V 和b :
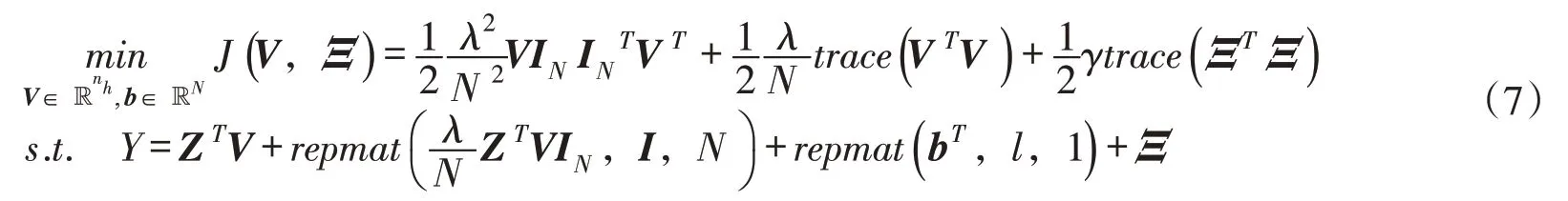
式中:IN=[1,1,…,1]T∈ℝN。
通过引入核函数(满足Mercer 定理)、消除W 和Ξ 得到线性方程组[37],并设方程组解为和b*,最终获得多输出模式下的决策函数f ( x ):
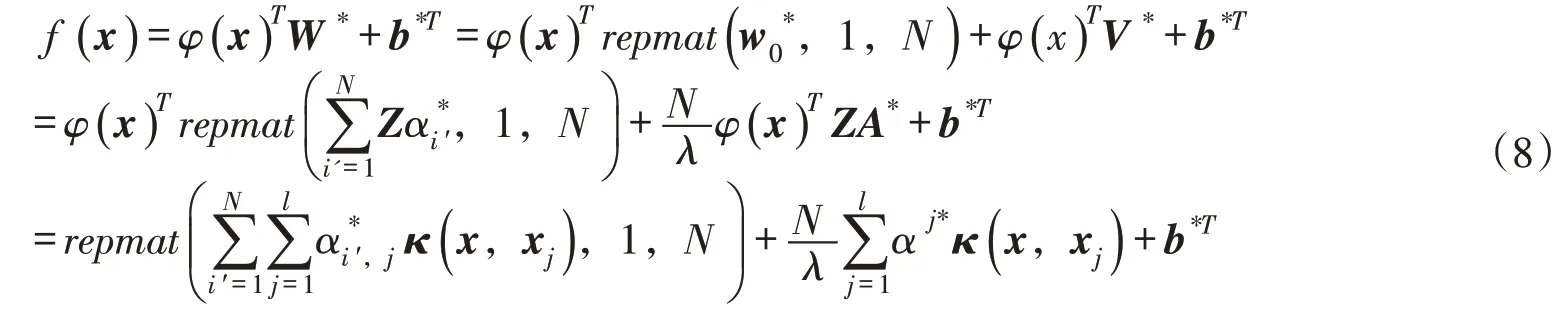
式中:κ(x,xj)表示核函数。
4 工程应用
基于上述动态建模方法,以某混凝土坝工程多测点变形监测数据为例,对CMCS模型进行有效性和准确性验证,旨在通过此实例说明CMCS在大坝变形建模方面的优越性。西南地区某水利枢纽主要由拦河大坝、右岸地下厂房及左岸坝后厂房、通航建筑物和两岸灌溉取水口组成,其控制流域面积为45.88万km2,总装机容量达775万kW,具有发电、防洪、灌溉和拦沙等综合效益。其中,拦河大坝坝顶高程384 m,最大坝高162 m,坝顶全长909.26 m,坝型为混凝土重力坝。现采用该坝某一坝段不同高程的垂线测点PL6Y(高程243 m)、PL6-1Y(高程260 m)、PL6-2Y(高程282 m)、PL6-3Y(高程322 m)以及PL6-4Y(高程350 m)方向变形监测数据(Y 方向表示与坝轴线垂直的方向),变形监测时段为2013 年10 月4 日—2017 年7 月9 日,共计5×230 个实测变形数据。利用三次Hermite 插值方法[38]对所选测点的变形原型观测数据进行均匀化处理,得到平均每周一次数据采集的插值结果(即步长以周(w)为单位),将其与环境量(如上游水位、气温等)监测数据汇总于图2中,以此为模型验证提供必要条件。
4.1 复杂关联性检验CMCS模型主要针对3种关联性并存的最复杂情况进行分析,故复杂关联性检验是该模型应用的先决条件。为验证考虑多维复杂关联性的必要性,利用耦合相关性诊断方法、动态最大信息系数和标准化动态时间规整算法分别检验大坝原型观测数据中的因子相关性、动态因果关系和序列相似性。
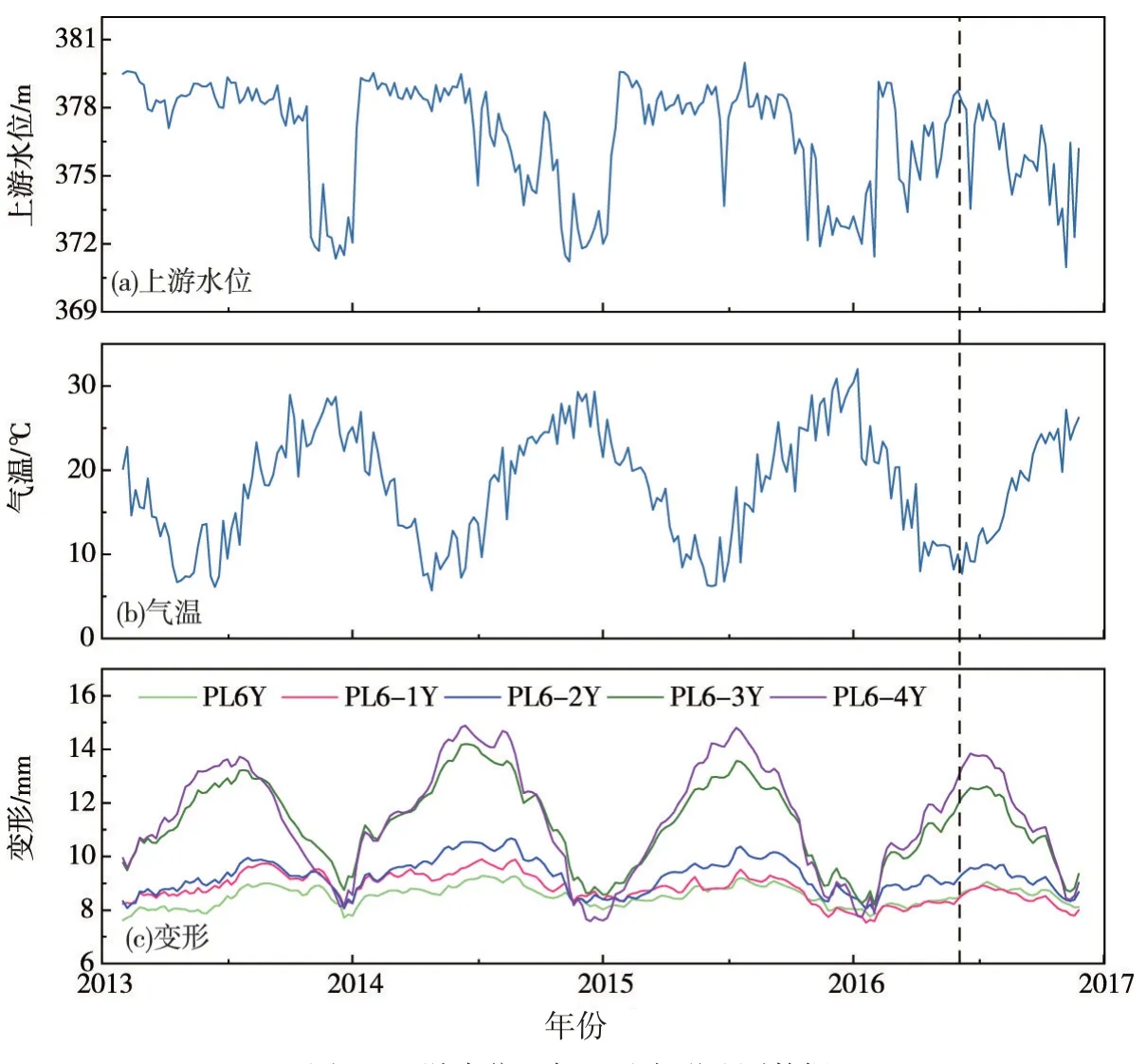
图2 上游水位、气温及变形监测数据
4.1.1 因子相关性检验 根据式(2)计算得到的因子相关性耦合诊断结果见表1。采用特征根判定法[27]得到最大条件数为223.83 >100,显示因子间存在较为严重的相关关系。因子H、H2、θ和lnθ所对应的VIF值均大于10,进一步说明因子相关性主要由上述4个解释变量所引起。经验证,H和H2、θ和lnθ的简单相关系数分别为0.99和0.98,呈现高度相关。此外,根据计算CI所得方差比例表[27],判定强相关因子组合有{H,H2,H3} 和{θ,lnθ },在表1中分别用“○”和“△”两种符号表示。与VIF仅判定H和H2为强相关因子有所不同,CI计算结果断定H3同为强相关因子,通过计算得知H和H3、H2和H3的简单相关系数均为0.99,最终证实H3确实参与导致因子相关性。综上,所选多测点变形监测数据中存在严重因子相关性,同时说明耦合VIF与CI能有效提高因子相关性的诊断率。
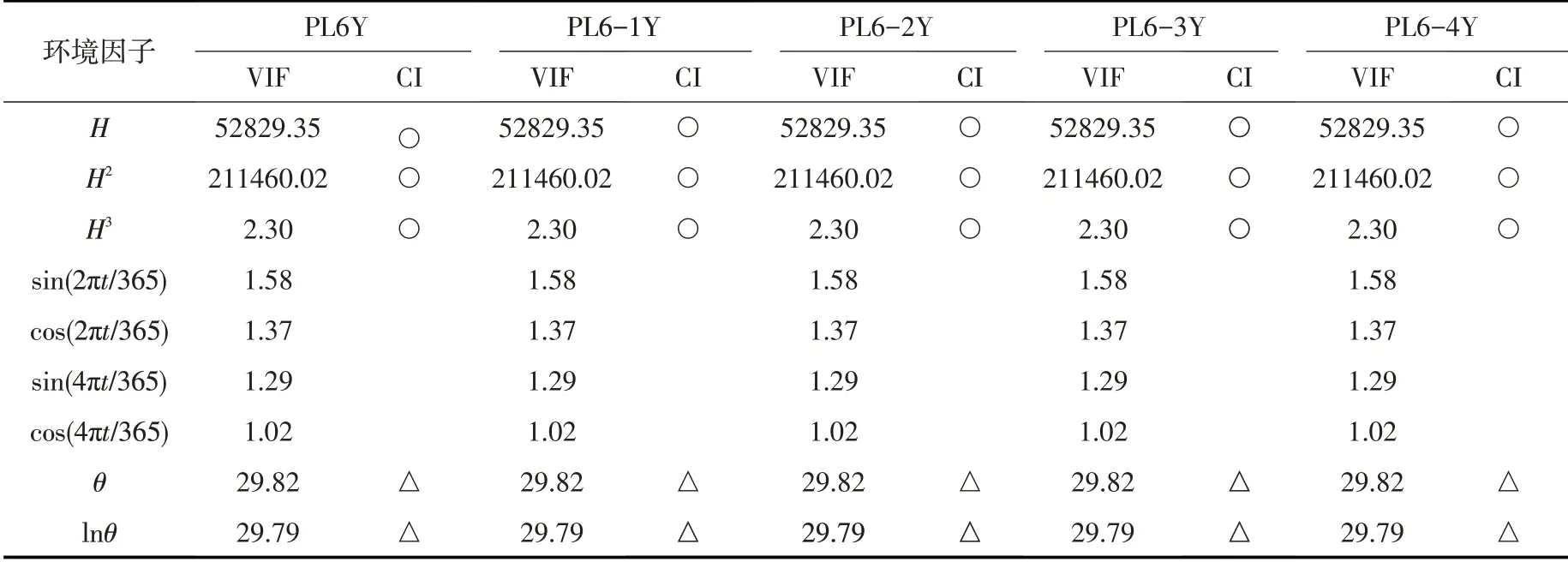
表1 因子相关性耦合诊断结果
4.1.2 动态因果关系检验 不同环境因子与多测点变形数列间的动态因果关系度量结果如图3 所示(由于DMIC不受解释变量间显式函数关系的影响,特将H、H2、H3和θ、lnθ作统一展示)。DMIC值越大,表示因果关系越显著。从图3中得知:(1)水位因子H、H2和H3与5个测点变形数列的动态演化过程基本一致。图形整体波动较大,多数DMIC值小于0.5,说明水位对变形的影响相对较小,且持续时间较短。(2)温度因子sin(2πt/365)、cos(2πt/365)、sin(4πt/365)和cos(4πt/365)与各测点变形数列的动态演化过程存在差异,但总体上PL6Y 和PL6-1Y、PL6-3Y 和PL6-4Y 演化过程较为接近,说明不同高程下温度对变形的影响虽有不同,却有规律可循。与图3(a)相比,图形整体波动减小,DMIC值增大,表明温度对变形的影响相对较大,且具有一定持续性。(3)时效因子θ、lnθ与各测点变形数列的动态演化过程差异显著,表示不同高程下时效对变形的影响明显不同。图3(f)中,图形整体波动进一步减小,DMIC值大多维持在0.75以上,尤以PL6-3Y和PL6-4Y演化过程为甚,说明时效对变形的影响持续显著。较之于上述动态演化过程,静态因果关系MIC度量结果(见表2)仅能表明不同高程下时效因子θ 和lnθ 对变形的影响较大。由此可见,通过度量动态因果关系能够提高环境量、变形等监测数据的潜在信息利用率。

图3 不同环境因子与多测点变形数列间的动态因果关系度量结果

表2 静态因果关系MIC度量结果
4.1.3 序列相似性检验 多测点变形数列相似性度量结果如图4所示。NDTW值越小,表示两变形数列间相似性越高。由图4可知,PL6-3Y和PL6-4Y相似度最大,随后是PL6-2Y和PL6-3Y,其余数列对NDTW值均介于10到20之间。简言之,5个测点变形数列中PL6-2Y、PL6-3Y和PL6-4Y三者较为相似,表明同一坝段不同高程的垂线测点变形数列存在明显交叉相似性。

图4 多测点变形数列相似性度量结果
4.2 CMCS模型应用由4.1可知,所选多测点变形监测数据中存在因子相关性和序列相似性,故采用CMCS模型对其进行大坝变形动态建模分析。根据3.1节统计理论推导,模型输入因子集统一确定为{H , H2, H3,sin(2πt 365),cos(2πt 365),sin(4πt 365),cos(4πt 365),θ ,}lnθ ,结合3.2节DNCT方法和4.1.2节动态因果关系度量结果,得到动态修正后的输入因子集分别为{DMIC1хnH,cos(4πt 365),DMIC8×nθ,DMIC9×nlnθ },n=1,2,…,5,对应模型输出则为PL6Y、PL6-1Y、PL6-2Y、PL6-3Y以及PL6-4Y等5个测点的变形量。为验证CMCS模型的可行性和有效性,本文变形预测仿真实验设定实测步长为200w(2013年10月4日—2017年1月10日,数据示于图2中竖线以左)、预测步长为30w(2017年1月16日—2017年7月9日,数据示于图2中竖线以右),模型应用步骤简述如下:(1)输入因子集归一化处理;(2)选取径向基函数(radial basis function,RBF)作为核函数,即初始化模型参数(γ,λ,p ),其中p 为正则化常数;(3)采用网格搜索和10折交叉验证拟合实测期数据以寻求最优参数组合并求解超参数α 和b ;(4)以交叉多输出模式为基础,利用预测期数据测试CMCS模型的多测点变形预报性能。
在大坝变形建模研究中,均方根误差(root mean squared error,RMSE)、平均绝对误差(mean ab⁃solute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)和最大误差(maxi⁃mum error,ME)是评价大坝变形监控模型性能较为常用的4项统计指标[38-40]。
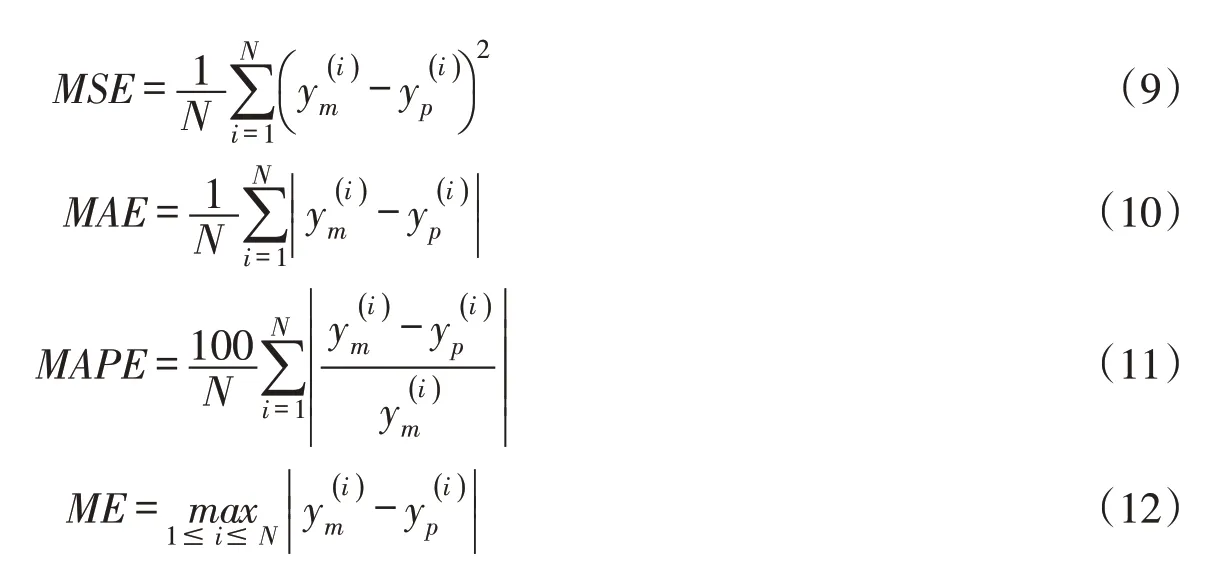
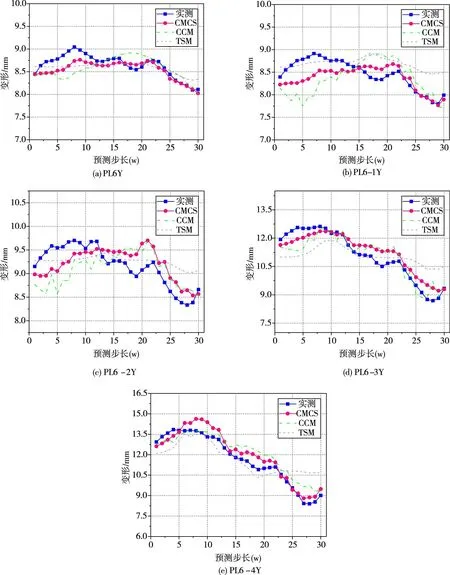
图5 多模型在不同测点变形预测中的性能对比结果
4.3 多模型性能评估为凸显CMCS模型的优势,现将其与同样基于SVM构建的时间序列模型(time series model,TSM)、常规因果模型(conventional causal model,CCM)进行性能对比,以上模型在5个测点变形预测中的性能对比结果如图5所示。从图5可以看出:(1)TSM模型对15w内的整体趋势把握较准,15w外其预测趋势出现较大偏离。该模型预测变形曲线较为平滑,故其难以预测局部波动。(2)相比于TSM模型,CCM模型变形预测值与实测值波动匹配度更高,但仍有部分时间段偏差较大。该模型预测变形曲线起伏较大,说明其对环境因子变化较为敏感。(3)三者中,CMCS模型在整体趋势外推、局部波动拟合等方面的性能均比TSM、CCM模型优越,可见融合多维复杂关联性对于大坝变形监控模型性能的改善起到一定作用。上述三种模型在不同测点变形预测中的性能量化评估结果(详见表3 和表4)亦能证明这一观点。就本文所选变形监测数据,各模型对高程300 m 以下PL6Y、PL6-1Y和PL6-2Y三测点变形预测效果按照统计指标(见表3)从优到劣排序为CMCS>TSM>CCM,而对高程300 m 以上PL6-3Y 和PL6-4Y 两测点变形预测效果按照统计指标(见表4)从优到劣排序为CMCS>CCM>TSM。总体而言,考虑动态因果关系和序列相似性的CMCS模型对该坝段多测点变形监测数据的适应性尤佳。

表3 多模型在测点PL6Y、PL6-1Y和PL6-2Y方向变形预测中的性能量化评估结果

表4 多模型在测点PL6-3Y和PL6-4Y方向变形预测中的性能量化评估结果
5 结论
本文提出一种兼顾相关性和相似性的大坝变形动态监控模型,其采用多种关联性量化和数学建模方法将因子相关性、动态因果关系和序列相似性集成于同一建模框架中,既能促进模型的一体化构建,又能实现对大坝变形监测数据的准确分析。基于所提出的动态建模方法,结合某混凝土坝工程多测点变形监测数据进行多模型性能对比仿真实验,结果表明该模型在变形预报方面优势明显,主要表现为:(1)内置多维复杂关联性检验方法,可通过量化关联性来灵活调整大坝变形动态建模的流程;(2)采用动态最大信息系数真实还原环境因子与大坝变形间的演化过程,以实现对输入因子的动态非线性修正;(3)将多测点变形数列间的相似性融入大坝变形监控模型,增加信息维度的同时,还能完成多测点变形预报;(4)根据多测点变形特性差异,通过网格搜索赋予模型以参数寻优能力,从而完成指向性模型的建立;(5)充分考虑多维复杂关联性,使大坝变形监控模型的预测性能得以改善。
鉴于大坝变形动态监控模型能够集成解释变量、响应变量以及两者间的多种关联性,更适合应用于各坝段多测点变形监测数据的有效预报。考虑到该模型仅融合了三种关联性,仍有部分隐含信息未被顾及,故后续将重点研究大坝变形与多因子耦联系统的演化规律,并将所得有效信息纳入到模型中。

