苹果采摘机器人末端执行器恒力柔顺机构研制
苗玉彬,郑家丰
苹果采摘机器人末端执行器恒力柔顺机构研制
苗玉彬,郑家丰
(上海交通大学机械与动力工程学院,上海 200240)
为了减少采摘机器人末端执行器在夹持过程中对果实造成的损伤,该文通过在末端执行器上设置柔顺机构,并对柔顺机构力学性能进行计算,求解果实无损采摘所需的柔顺恒力特性。首先,基于形状函数建立边界条件约束下的柔顺梁非线性常微分控制方程;然后,利用打靶法将上述边值问题重新描述为初值问题,并结合遗传算法进行初值优化求解,采用序列二次规划法优化梁的形状函数,使其在一定变形范围内实现恒力输出;最后,在给出求解所需参数和柔顺机构初始形状参数基础上,以苹果采摘为例,通过优化计算,使柔顺梁对果实的夹持力维持在7.9 N左右,非线性有限元计算和力-位移特性试验验证了计算结果的准确性,多次苹果夹持试验的抓取完好率为95%,验证了该柔顺机构无损夹持苹果的可行性。研究结果可为不同类型果实的恒力夹持提供参考。
机器人;末端执行器;设计;恒力柔顺机构;打靶法
0 引 言
采摘作业是果蔬生产中最耗时、费力的一个环节。随着农业劳动力的减少,农业生产成本相应提高,果蔬采摘机器人逐渐成为农业机器人领域的研究热点[1]。果实的无损采摘是采摘机器人的关键技术之一[2-7],主要通过末端执行器和作物果实直接接触。由于果实一般比较脆弱柔软,形状及生长状况比较复杂,采摘过程中夹持力过大容易造成果实表面或内部损伤,而夹持力不足又无法抓牢果实。因此,合理地优化设计末端执行器,实现对果实的柔顺抓取,是实现果实无损采摘的研究重点。
目前末端执行器无损夹持一般基于力的反馈控制实现,即利用压力传感器实时测量对果实的夹持力,将实际输出与期望输出对比构成闭环控制,使夹持力保持恒定。如王学林等[8]提出基于灰色预测的增量式比例积分力控制算法,根据预测模型的精度调整预测力偏差所占的权重,计算出稳定控制夹持力的校正量。周俊等[9]以当前抓取力和滑动信号小波变换的细节系数作为控制器的输入,末端执行器闭合的距离作为控制器的输出,采用混合学习算法结合减法聚类算法进行训练,使抓取力超调量得到有效限制。Dimeas等[10]提出基于模糊控制的分层递阶控制策略,通过模糊控制器调节采摘草莓的抓取力。但由于受到成本和使用环境等因素限制,精确控制的末端执行器难以在农业领域得到广泛应用[11]。
近年来,柔顺机构引起广泛关注。柔顺机构是一种依靠机构中柔性构件的变形来完成全部运动,从而实现力或能量传递的机构[12-16]。柔性构件的应用使得在一定范围内可以进行恒力输出,减少恒力机构对力传感和控制的需求。如张赢斌[17]研究了柔顺钳和柔顺恒力机构设计的拓扑优化,采用相对密度法和非线性有限元方法对柔顺钳进行了优化设计。Merriam等[18]借助遗传算法和有限元建模控制柔顺伸缩器的结构参数,使其具有一定范围内的恒力输出。Wang等[19]用打靶法设计静平衡机构和恒力机构,将它们串联得到有稳定恒力输出的恒力夹钳,并使用有限元模型和实物模型验证结果。Pham等[20]参考柔性双稳态机构设计人字形柔顺屈曲梁,通过非支配排序遗传算法优化梁的形状实现输出力的调节。Liu等[21]采用倾斜的基于弯曲梁的柔性双稳态机构来构造负刚度机构,设计了一种新型的柔性钳,并采用非开关变结构控制算法克服滞后效应。
显然,如果能利用恒力柔顺机构对果蔬采摘机器人的末端采摘夹持器进行合理设计,在保持对果实可靠夹持的同时将夹持力控制在一定范围,则既可以降低末端夹持装置的复杂度,也能减少甚至避免对果实的夹持损伤。但现有的柔顺恒力机构往往存在恒力区间相对机构尺寸小的缺陷,难以应用在果实采摘等要求结构设计紧凑的场合。为此,本文针对果实柔顺夹持问题,在末端执行器的驱动机构和夹钳之间设置柔顺屈曲梁,并结合打靶法、遗传算法计算求解柔顺机构的数学模型,利用序列二次规划法设计优化柔顺机构的相关参数,使末端执行器在一定位移输入范围内具有恒力输出特性,并可根据夹持力大小调整,从而实现对果实的恒力夹持。
1 柔顺夹持机构设计与分析
1.1 采摘夹持器柔顺设计
末端执行器按手爪个数可分为2指和多指型,用于苹果等球状果实的夹持器通常为弧形二指或三指结构[8,22-23],夹持手指采用弧面结构以增大和果实的接触面积、减少损伤。这种夹持器一般使用电动或气动装置驱动手指抓取果实,手指弧面上安装有压力传感器获取夹持力反馈,用以调节位移输入。
以二指式末端执行器为例,图1为二指式果实夹持末端执行器模型。当二指机构与果实接触时,假定2指相对平行,则果实每侧所受挤压合力方向与该侧机械手指的位移输入方向相同,如图1a所示。如果在驱动机构和弧面手指之间设置屈曲梁或类似柔顺机构,当柔顺机构的形状满足特定条件时,在一定位移输入范围内柔顺机构变形,产生类似“超弹性”效果,使弧面手指保持恒力夹持,如图1b所示。

注:Fin为输入力,N;yin为位移输入,cm;L1、L2分别为2段梁的长度,cm;t为柔顺梁宽度,cm;w为柔顺梁厚度,cm;n1、n2、n3为柔顺梁节点,下同
由于结构的对称性,取一侧柔顺机构进行计算,如图1c所示。柔顺机构由长为1和2的2段柔顺梁组成,记为梁1和梁2,每段柔顺梁均具有矩形横截面,其中梁厚度为,宽度为以点1为坐标原点保持不动,点3处有竖直方向的位移量in。
图2为柔顺梁的大挠度变形模型,未变形的柔顺梁由形状函数()描述[24],其中∈[0,1],是沿中性轴的无量纲弧长,表示柔顺梁相对轴的倾斜角度,rad。当受到外部负载时,偏转梁由另一个函数()表示,rad。柔顺梁受到的和方向的外力分别表示为F和F,N。中性轴上的任意点(,)表示为:

式中(0),(0)表示无量纲弧长=0时的坐标,cm;为梁的长度,cm。
注:F和F分别为和方向的支反力,N;∈[0,1],是沿中性轴的无量纲弧长;()表示未变形梁和轴的夹角,rad。()表示变形梁和轴的夹角,rad。
Note:FandFare reaction forces in theanddirections respectively, N;∈[0,1] is the dimensionless arc length along the neutral axis;() represents the angle between the undeformed beam and the-axis, rad;() represents the angle between the deformed beam and the-axis, rad.
图2 柔顺梁的大挠度非线性变形模型
Fig.2 Nonlinear large deformation model of compliant beam
将未变形梁的形状函数利用多项式进行参数化处理,如式(2)所示。

其中系数c0~c表征第段梁的形状,将其描述为+1次多项式曲线。
根据文献[25],柔顺梁的控制方程为:
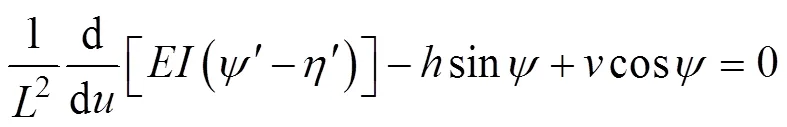
式中为梁的抗弯刚度,其中是弹性模量,MPa;截面惯性矩=312,cm4;和分别等于F和F,N。
梁上的应力(MPa)如式(4)所示。
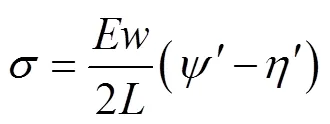
1.2 柔顺梁变形模型的打靶法求解
以无量纲弧长为自变量,由式(1)、式(3)可得到控制梁变形的常微分方程组为:
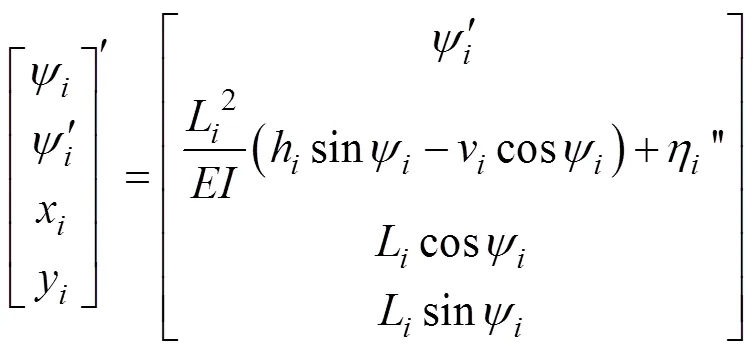
式中下标=1,2分别表示图1c中长度为1和2的2段梁。根据梁的力平衡、力矩平衡、转角连续和几何约束等条件,式(5)须满足以下初始条件和边界条件:
1)在点1处:
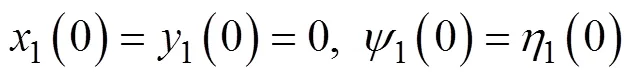
2)在点2处:

3)在点3处:

取梁形状参数中=2,此时梁形状曲线为三次多项式曲线,已能保证梁形状的多样性。当梁的控制参数10,11,12,20,21,22,1,2确定时,记未知初值1¢(0)为,整理得初值条件为
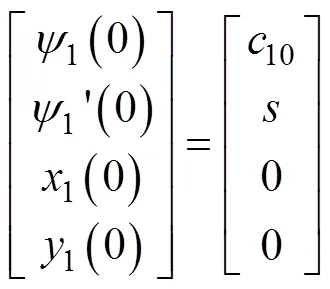
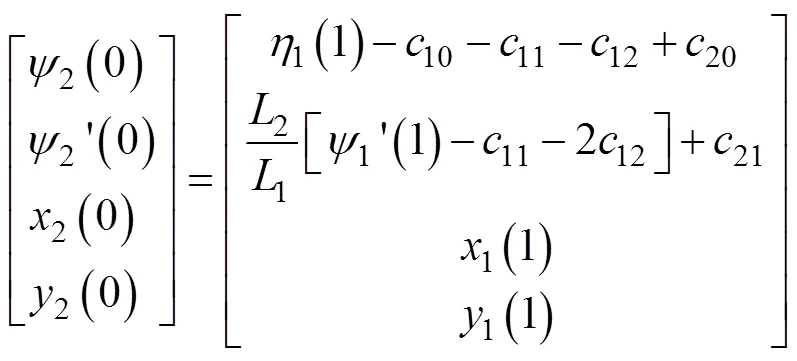
终值条件为

式(5)、(9)~(11)组成的非线性二阶常微分方程组中含2个未知参数、和1个未知初值,其终值处有3个边界条件,故可求解。本文采用打靶法[26]将边值问题转换为初值问题求解该微分方程组。为保证初值问题的求解精度,使用Matlab中的ode45函数[27],即变步长的龙格库塔法求解。将求解的结果终值与式(11)联立得到三元非线性方程组。
该三元非线性方程组的求解需要给出适当的初值,否则容易陷入局部收敛。为此本文将此方程组的求解视作优化问题,首先使用具有全局优化能力的遗传算法[28]得到一组可行解,并将该组解作为初值,代入到Matlab的fsolve函数,最终得到方程组的解。
方程组的解中等于y,为节点3在位移至in处时该点沿位移输入方向的支反力。将求得的解代入初值问题过程量中,得到、、¢,进而得到位移输入下柔顺梁的形状和梁上应力。柔顺梁模型的求解过程如下:
1)给定梁优化的初值1、2、1、2。
2)通过ode45函数建立三元非线性方程组。
3)通过fsolve函数结合遗传算法求解步骤2)中的非线性方程组得到未知参数、和未知初值。
4)将步骤3)中的解代入ode45函数数值求解每一步的函数值得到¢。
5)以¢建立1.3节中优化的目标和约束。
6)在优化过程中重复步骤1)~4),直至达到局部最优的1、2、1、2值,即最优柔顺梁模型。
1.3 柔顺梁模型优化
由式(1)~(2)可知,柔顺梁模型的控制参数为10,11,12,20,21,22,1,2,为使一定位移输入内的输出力F保持恒定,使和这2个位移输入下的输出力尽量接近,定义函数()表示输出力和位移输入的关系,则柔顺梁的优化模型可定义如下:

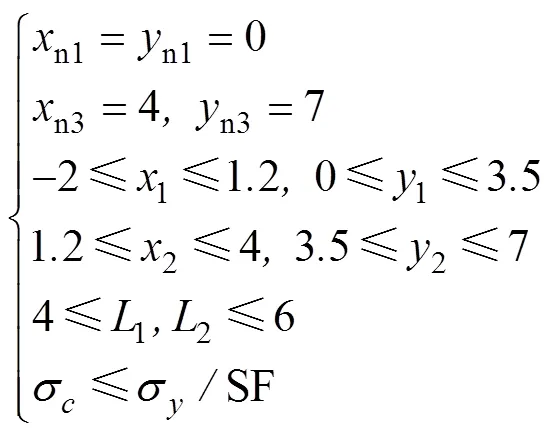
其中n1,n1,n3,n3分别为节点1和3的坐标,1,1,2,2分别为2段梁各点坐标,在梁模型求解步骤4)求得,cm。固定节点位置可以控制梁的设计边界和坐标取值范围,确保2段梁保持在一定边界内,防止2段梁互相交叉。限制2段梁的长度1和2,可以防止梁发生自身交叉。上述变量的约束如图1c中的虚线框所示,可根据柔顺梁在末端执行器上的尺寸调整。位移输入为时的应力c由式(4)求得,用于限制最大变形时梁的最大应力不超过许用应力,y是屈服应力,MPa。SF是安全系数。
式(13)为模型的约束条件,以保证优化后的柔顺梁形状能够满足末端执行器大小需求。梁模型优化为非线性最优化问题,采用序列二次规划法(SQP,sequence quadratic program)[29]求解。但SQP为局部最优化算法,其初值的选取会影响最终优化结果,故此首先需要根据柔顺机构特点定义梁的相对合理的初始形状,再利用SQP算法进行优化。
2 柔顺梁优化与试验
2.1 柔顺梁模型优化
采用前述优化算法对苹果夹持末端执行器柔顺梁模型进行优化和求解。根据柔顺梁3D打印使用的聚甲醛材料和期望的恒力输出区间,设定优化的相关参数为:弹性模量=2.6 GPa,屈服应力y=76 MPa,安全系数SF=1.5,=0.7 cm,=2 cm,最大允许应力下的位移输入=2.2 cm,梁宽度=10 mm,梁厚度=1 mm。
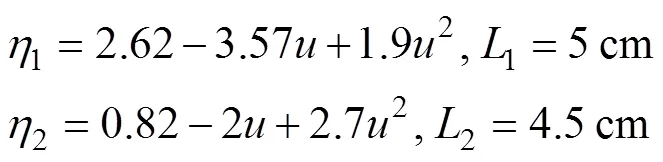
优化后得到梁的形状参数为:

根据梁模型求解步骤4)得到优化后柔顺梁的初始形状和受到位移输入作用后的变形形状,如图3所示。柔顺梁的3个节点位置和2段梁的位置受优化模型中的约束条件限制,约束取值可按需求设置。柔顺梁的最大应力出现在节点1处。柔顺梁存在恒力输出段的原因如下:由图4中梁2的变形趋势可见梁2在位移输入方向上的刚度(抵抗变形的能力)随位移输入而减小,由正刚度结构变为负刚度结构。由梁1变形趋势可见梁1始终为正刚度结构,梁1起到辅助梁2变形的作用。当2段梁在位移输入方向上的刚度之和接近零刚度时,将存在一段输出力不随位移输入发生变化的范围。
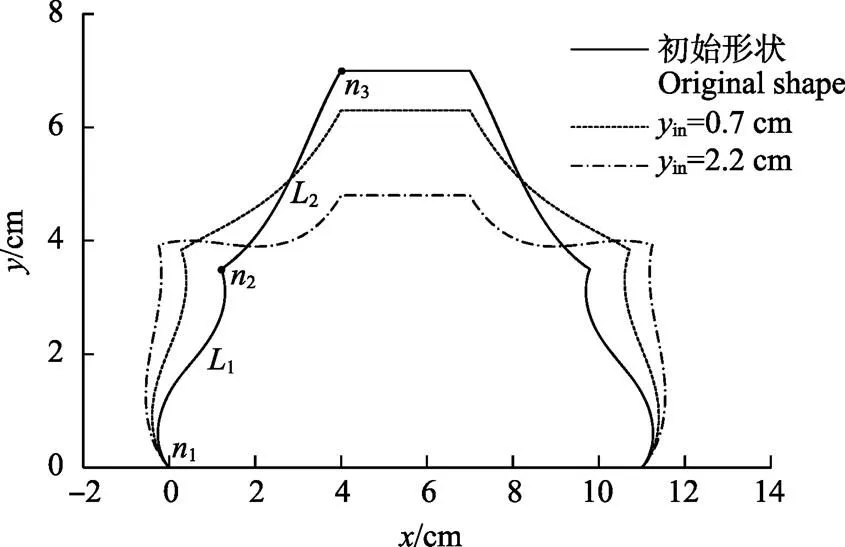
图3 柔顺梁变形过程图
图4为优化前后柔顺梁的力-位移曲线,其中()=3.911 6 N,()=3.960 5 N,并在最大位移处达到许用应力48.1 MPa。当夹持器夹取果实时,在0~位移范围内夹持力持续增加,在~范围内夹持力保持基本恒定,从而在不需要力反馈的条件下,实现了对果实的恒力柔顺夹取。其恒力范围可根据式(12)、式(13)进行调整。相比之下,优化前的柔顺梁无“零刚度”段,夹持力随位移输入增大而明显变化,无法实现恒力夹持。

注:a~c表述优化时设定的恒力位移区间。
此外,由图4中~恒力段数据,单侧柔顺梁对苹果的夹持力约为3.95 N左右,夹持合力约为7.9 N,波动误差不超过0.1 N。根据文献[30]中的苹果抓持试验,以300 g苹果为例,与夹持指摩擦系数为0.5时稳定抓取的力不小于3 N,当夹持力超过20 N(生物屈服力)后苹果的内部组织将受到损伤,本文的优化结果满足苹果无损稳定采摘要求。当需要调整恒力大小时,不改变梁优化形状即可实现,由式(3)知相同位移输入下的支反力大小与抗弯刚度正相关。通过改变梁厚度或宽度可使梁具有不同的抗弯刚度,从而调整优化后柔顺梁提供的恒力大小,使其适应不同种类果实的无损采摘需求。需要注意的是,梁厚度将影响梁受到的应力,当取较大值时,相同载荷下的应力增大,将限制柔顺机构的操作范围。
2.2 柔顺梁力-位移特性仿真与试验
为验证本文方法的正确性,分别利用非线性有限元仿真和柔顺梁力-位移特性试验对上述结果进行对比验证。为了加工方便和便于观察试验效果,对恒力结构进行了适当放大。实际使用时,一方面可结合连杆机构将柔顺梁设置在合理位置而不是夹钳上,另一方面可以将恒力结构的尺寸和恒力范围缩小,通过机构并联的方式实现期望的输出特性,从而大大减小结构尺寸。
试验装置如图5所示,柔顺梁形状参数与文中优化结果相同,使用聚甲醛材料通过3D打印加工而成,其弹性模量和屈服应力与优化时的材料参数设置一致。位移输入装置为步进电机驱动的线轨滑台模组(盛斯达T6/4-200 mm,精度0.1 mm,水平最大负载2.5 kg)。装置中柔顺梁、丝杆导轨和数显百分表(型号为BFQ-350A,量程50.8 mm、精度±0.02 mm)均固定,载物平台在步进电机驱动下在丝杆导轨上移动并通过拉压力传感器(型号为JLBS-M2-3KG,量程3 kg,精度0.05%)对柔顺梁施加位移输入,力传感器测量作用力数值,数显百分表测量位移数值,力与位移一一对应得到力-位移曲线。

1. 数字百分表 2. 丝杠导轨 3. 载物平台 4. 力传感器 5. 柔顺梁
非线性有限元仿真在有限元分析软件Abaqus中进行,以柔顺梁优化结果的形状建立梁单元模型,设定弹性模量为2.6 GPa(与优化参数相同),边界条件如图1c所示(1固支,3设置位移输入且限制其他方向自由度),并划分为866个网格单元,记录3位移输入和1相应的支反力。
图6为Abaqus仿真结果中位移输入为2.2 cm时梁的应力云图,其中最大应力47.87 MPa,与本文算法的实际计算结果48.10 MPa误差为-0.48%。Abaqus对梁的力-位移关系对比验证结果如图7所示,位移输入范围0.2~2.8 cm,间隔0.2 cm,共14个点。仿真结果与计算相比,支反力平均误差为-0.007 N,平均相对误差-0.18%,最大误差为-0.038N,最大相对误差-0.96%,计算结果精度较高,表明本文梁模型的计算方法理论可行。
测试试验的位移输入范围0.2~2 cm,间隔0.05 cm,共37个测点。与本文模型计算结果相比,试验测得的支反力平均误差为0.198 N,平均相对误差5.06%,最大误差为0.215 N,最大相对误差5.8%。试验结果与计算结果大致吻合,说明本文梁模型实际可实现。图中试验结果比计算、仿真值稍大,而仿真结果、计算结果吻合,其主要原因是仿真分析和计算的理论模型只考虑了中性轴的变形,而实际中存在梁厚度,使得连接处的刚性比理论模型稍大,同时也存在打印加工误差和材料弹性模量误差,使试验结果相对理论分析值产生偏差。
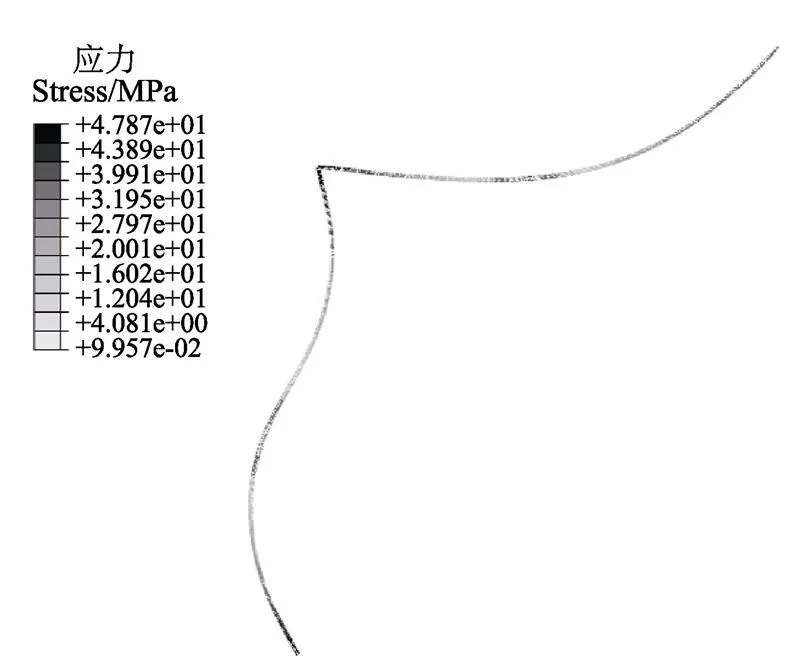
图6 位移输入为2.2 cm时柔顺梁应力云图

图7 力-位移特性验证结果
2.3 苹果抓取试验
采用文中机构对苹果进行柔顺夹持,夹持试验装置如图8所示,力传感器与验证试验相同。夹持指Ⅰ固定不动,夹持指Ⅱ通过力传感器安装在载物平台上。在步进电机驱动下,载物平台在丝杆导轨上移动,带动夹持指Ⅱ与夹持指Ⅰ合拢夹紧苹果,载荷大小由力传感器读取。
以1次抓取试验为例,图9为抓取苹果时柔顺梁夹持力随时间变化曲线,将载荷开始增大的时间记为0时刻。从夹持指Ⅰ开始接触苹果时载荷开始迅速增大,当夹持力大约达到8 N时进入柔顺梁的恒力范围;随时间增加,步进电机继续驱动夹持指夹紧,夹持力基本稳定。取夹持力稳定段4~7 s共150个数据点进行分析,得到支反力波动范围为7.46~8.42 N,平均支反力为8.03 N,与模型计算值的误差为1.6%,与力-位移验证试验结果的误差为-0.84%。由此可见,实际苹果夹持时虽然夹持力有一定波动,但夹持恒力与计算结果基本相符。
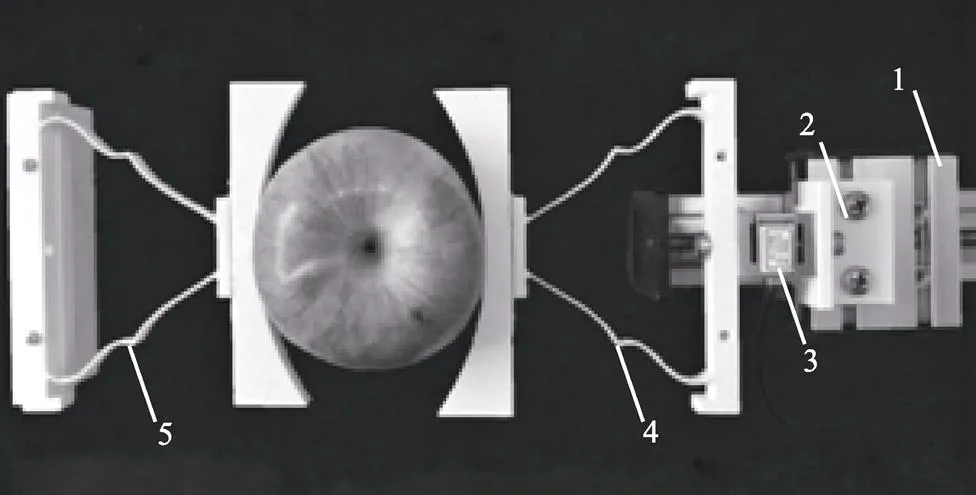
1. 丝杠导轨 2. 载物平台 3. 力传感器 4. 夹持指Ⅱ 5. 夹持指Ⅰ
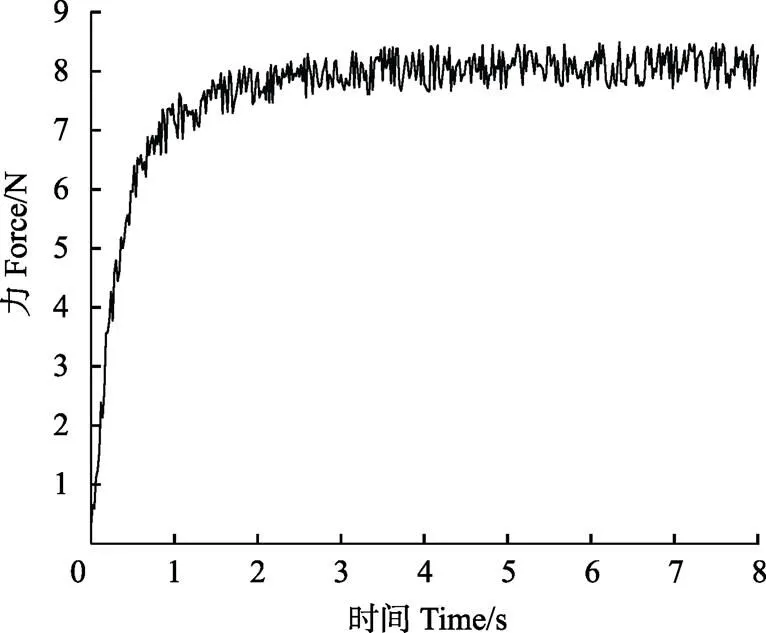
图9 苹果抓取试验夹持力
为进一步验证夹持机构的柔顺性,选取大小相近、表面完好的20个苹果进行抓取试验,夹持持续时间为 10 s,均没有发生滑落现象。将苹果静置24 h,人工观察苹果表皮只有1个苹果表面出现坏点抓取完好率为95%。由于夹持力未达到苹果的生物屈服力,该苹果内部未发生损伤,其表面损伤的原因可能是由于表面与夹持指不贴合,导致局部压强较大。
3 结 论
1)针对果蔬采摘机器人无损采摘需求,通过在末端执行器上设置柔顺机构,并对柔顺机构的力学性能进行优化计算,获取果实无损采摘所需的柔顺恒力特性。
2)建立柔顺梁的变形控制微分方程组,采用打靶法将边值问题重新描述为初值问题,并结合遗传算法优化求解初值。在此基础上,采用序列二次规划法优化计算梁的形状函数,使柔顺梁对苹果的恒定夹持力维持在7.9 N左右。
3)分别进行非线性有限元仿真和柔顺梁力-位移特性试验,仿真与模型计算结果相符,试验与模型计算结果平均误差为5.06%。进行苹果抓取试验,夹持力波动为7.46~8.42 N,平均恒定夹持力约为8.03 N,满足苹果无损夹持需求。
4)多次苹果夹持试验的抓取完好率为95%,验证了该柔顺机构无损夹持苹果的可行性。通过适当调整柔顺梁的参数,本文算法可适应不同类型果实的恒力夹持需求,可为柔顺机构在果蔬无损夹持采摘中的有效应用提供参考。
[1] 宋健,张铁中,徐丽明,等. 果蔬采摘机器人研究进展与展望[J]. 农业机械学报,2006,37(5):158-162. Song Jian, Zhang Tiezhong, Xu Liming, et al. Research actuality and prospect of picking robot for fruits and vegetables[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(5): 158-162. (in Chinese with English abstract)
[2] Liu F, Ji W, Tang W, et al. Research on grasping planning for apple picking robot’s end-effector[C]//Proceedings of the 2015 Chinese Intelligent Systems Conference. Berlin Heidelberg: Springer, 2016: 95-103.
[3] Bac C W, Hemming J, Van Tuijl J, et al. Performance evaluation of a harvesting robot for sweet pepper[J]. Journal of Field Robotics, 2017, 34(6): 1123-1139.
[4] 徐丽明,刘旭东,张凯良,等. 脐橙采摘机器人末端执行器设计与试验[J]. 农业工程学报,2018,34(12):53-61. Xu Liming, Liu Xudong, Zhang Kailiang, et al. Design and test of end-effector for navel orange picking robot [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(12): 53-61. (in Chinese with English abstract)
[5] 傅隆生,张发年,槐岛芳德,等. 猕猴桃采摘机器人末端执行器设计与试验[J]. 农业机械学报,2015,46(3):1-8. Fu Longsheng, Zhang Fanian, Yoshinori G, et al. Development and experiment of end-effector for kiwifruit harvesting robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3): 1-8. (in Chinese with English abstract)
[6] Chiu Y C, Yang P Y, Chen S. Development of the end-effector of a picking robot for greenhouse-grown tomatoes[J]. Applied Engineering in Agriculture, 2013, 29(6): 1001-1009.
[7] Kondo N, Yamamoto K, Shimizu H, et al. A machine vision system for tomato cluster harvesting robot[J]. Engineering in Agriculture Environment & Food, 2009, 2(2): 60-65.
[8] 王学林,姬长英,周俊,等. 基于灰色预测控制的果蔬抓取系统设计与试验[J]. 农业工程学报,2010,26(3):112-117. Wang Xuelin, Ji Changying, Zhou Jun, et al. Design and experiment of fruit and vegetable grasping system based on grey prediction control[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(3): 112-117. (in Chinese with English abstract)
[9] 周俊,杨肖蓉,朱树平. 基于自适应神经模糊网络的果蔬抓取力控制[J]. 农业机械学报,2014,45(7):67-72. Zhou Jun, Yang Xiaorong, Zhu Shuping. Fruit and vegetable grasping force control based on adaptive neural fuzzy network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(7): 67-72. (in Chinese with English abstract)
[10] Dimeas F, Sako D V. Design and fuzzy control of a robotic gripper for efficient strawberry harvesting[J]. Robotica, 2015, 33(5): 1085-1098.
[11] 章军. 六关节三指苹果抓取机械手的自适应柔性分析[J]. 农业工程学报,2010,26(1):140-144. Zhang Jun. Analysis of adaptive flexibility of three-finger manipulator with six-joint for grasping apple[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(1): 140-144. (in Chinese with English abstract)
[12] Ling M , Cao J , Jiang Z , et al. Development of a multistage compliant mechanism with new boundary constraint[J]. Review of Scientific Instruments, 2018, 89(1): 015009.
[13] Zhang X, Zhu B. Topology optimization of compliant mechanisms[M]. Singapore: Springer Singapore. 2018.
[14] Li Y, Chen Y, Yang Y, et al. Passive particle jamming and its stiffening of soft robotic grippers[J]. IEEE Transactions on Robotics, 2017, 33(2): 446-455.
[15] 张爱梅. 平面梁大挠度非线性问题的完备解与柔顺机构精确建模[D]. 西安:西安电子科技大学,2013. Zhang Aimei. Comprehensive Solution to Nonlinear Large-Deflection Problems of Planar Beams and Accurate Modeling of Compliant Mechanisms[D]. Xi’an: Xidian University, 2013. (in Chinese with English abstract)
[16] 李庚. 空间大挠度梁的变形计算及其在空间柔顺机构建模中的应用[D]. 西安:西安电子科技大学,2016. LI Geng. Deformation Calculation of Spatial Large Deflection Beam and its Application on the Modeling of Spatial Compliant Mechanisms[D]. Xi’an: Xidian University, 2016. (in Chinese with English abstract)
[17] 张赢斌. 拓扑优化法设计柔顺恒力机构[D]. 西安:西安电子科技大学,2012. Zhang Yingbin. Design Compliant Constant Force Mechanism Using Topology Optimization[D]. Xi’an: Xidian University, 2012. (in Chinese with English abstract)
[18] Merriam E G, Colton M B, Magleby S, et al. The design of a fully compliant statically balanced mechanism[C]//ASME 2013 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. 2013, 6A(7): doi: 10.1115/DETC2013-13142
[19] Wang J Y, Lan C C. A constant-force compliant gripper for handling objects of various sizes[J]. Journal of Mechanical Design, 2014, 136(7): doi: 10.1115/1.4027285
[20] Pham H T, Wang D A. A constant-force bistable mechanism for force regulation and overload protection[J]. Mechanism & Machine Theory, 2011, 46(7): 899-909.
[21] Liu Y, Zhang Y, Xu Q. Design and control of a novel compliant constant-force gripper based on buckled fixed-guided beams[J]. IEEE/ASME Transactions on Mechatronics, 2016, 22(1): 476-486.
[22] 姬伟,李俊乐,杨俊,等. 机器手采摘苹果抓取损伤机 理有限元分析及验证[J]. 农业工程学报,2015,31(5): 17-22. Ji Wei, Li Junle, Yang Jun, et al. Analysis and validation for mechanical damage of apple by gripper in harvesting robot based on finite element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(5): 17-22. (in Chinese with English abstract)
[23] 姬伟,罗大伟,李俊乐,等. 果蔬采摘机器人末端执行器的柔顺抓取力控制[J]. 农业工程学报,2014,30(9):19-26. Ji Wei, Luo Dawei, Li Junle, et al. Compliance grasp force control for end-effector of fruit-vegetable picking robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(9): 19-26. (in Chinese with English abstract)
[24] Lan C C, Wang J H, Chen Y H. A compliant constant-force mechanism for adaptive robot end-effector operations[C]// Proceedings of the IEEE International Conference on Robotics and Automation. IEEE, 2010: 2131-2136.
[25] Lan C C, Cheng Y J. Distributed shape optimization of compliant mechanisms using intrinsic functions[J]. Journal of
Mechanical Design, 2008, 130(7): 3-11.
[26] Yin X, Lee K M, Lan C C. Computational models for predicting the deflected shape of a non-uniform, flexible finger[C]//Proceeedings of the IEEE International Conference on Robotics and Automation. IEEE, 2004: 2963-2968.
[27] 薛定宇,陈阳泉. 高等应用数学问题的MATLAB求解[M]. 北京:清华大学出版社,2004.
[28] John H. Mathews, Kurtis D Fink. 数值方法(MATLAB版)[M]. 北京:电子工业出版社,2005.
[29] 马昌凤. 最优化方法及其Matlab程序设计[M]. 北京:科学出版社,2010.
[30] 唐伟. 苹果采摘机器人末端执行器无损主动抓取技术研究[D]. 镇江:江苏大学,2017. Tang Wei. Research on Non-destructive and Active Grasp Technology for End-Effector of Apple Picking Robot[D]. Zhenjiang: Jiangsu University, 2017. (in Chinese with English abstract)
Development of compliant constant-force mechanism for end effector of apple picking robot
Miao Yubin, Zheng Jiafeng
(,,200240,)
In order to reduce the damage caused by end effector of picking robot during fruit clamping process, non-destructive fruit picking has gradually become a key technology of fruit harvesters. The application of compliant constant-force mechanism may enable a constant output force within a certain range of operating displacement. The existing compliant constant force mechanism has the defect that the constant force interval is small relative to the size of the mechanism, which makes it difficult to apply in the situations requiring compact structure design such as fruit picking. In this paper, a method to generate compliant constant-force mechanism is introduced. Firstly, based on the shape function, a set of nonlinear ordinary differential equations for buckling deformation of compliant beams under boundary conditions is established. Secondly, the boundary value problem is redescribed as the initial value problem by applying the shooting method combined with the Runge-kutta method, the 3D nonlinear equations are obtained according to three boundary conditions, two unknown variables and one unknown initial value. Thirdly, the nonlinear equations is solved as an optimization problem. To avoid the optimization problem falling into local convergence, the genetic algorithm is employed to globally find the appropriate initial values of the three unknowns in the nonlinear equations, the solution of the differential equations is obtained according to the principle of the shooting method. Finally, the sequential quadratic programming method is implemented to optimize the parameters of the shape function, the optimization objective is to achieve a constant output force within a certain range of displacement input, and the constraints are the design boundary and the maximum permissible stress of the beams. A two-finger apple picking end effector is taken as an example, the initial shape parameters of the compliant mechanism are set and the algorithm is realized in Matlab. After optimization, the constant clamping force of the compliant beam to the fruit is about 7.9 N. In order to verify the correctness of the method, the non-linear finite element simulation is carried out in Abaqus, and the force-displacement experiment is carried out. The simulation results agree well with calculations, compared to the calculations, the average error of force-displacement test is 5.06%, which is acceptable. The main reason for the error may be that the theoretical model only considers the deformation of the neutral axis. The apple picking test is designed to verify the practicality of the method. At constant-force range, the clamping force fluctuates from 7.46-8.42 N, and the average clamping force is about 8.03 N. The clamping force is basically consistent with the calculation results though a certain fluctuation exists. To further verify the flexibility of the clamping mechanism, 20 apples of similar size and intact surface are selected for clamping test. The result shows that the ratio of non-destructive grasping is 95%, no slipping occurred, the compliant mechanism designed can achieve stable clamping of apples. The algorithm can meet the requirements of constant force clamping for different types fruit by properly adjusting the parameters of the compliant beam. The research provides a reference for the effective application of the compliant mechanism in non-destructive fruit-picking.
robots; end effectors; design; compliant constant force mechanism; shooting method
10.11975/j.issn.1002-6819.2019.10.003
TP241
A
1002-6819(2019)-10-0019-07
2018-12-12
2019-01-15
上海市科研计划项目(16391901700);沪农科推字(2018)第1-2号、(2015)第4-1号;上海市工程技术研究中心建设专项(17DZ2252300)
苗玉彬,副教授,主要从事智能装备、智能传感器研究。Email:ybmiao@sjtu.edu.cn
苗玉彬,郑家丰.苹果采摘机器人末端执行器恒力柔顺机构研制[J]. 农业工程学报,2019,35(10):19-25. doi:10.11975/j.issn.1002-6819.2019.10.003 http://www.tcsae.org
Miao Yubin, Zheng Jiafeng. Development of compliant constant-force mechanism for end effector of apple picking robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(10): 19-25. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.10.003 http://www.tcsae.org

