无人机视觉的桥梁底面裂缝检测方法

贺志勇，王 鹏

（华南理工大学 土木与交通学院，广东 广州 510641）

0 引 言

为确保桥梁运营安全，必须及时进行检测评估。对在役桥梁进行快速、科学、准确检测，建立合适、便捷的检测评估方法已成为当务之急。目前桥梁检测以人工现场调查法为主。人工现场调查法存在工作量大、速度慢、效率低、漏检率高、费用昂贵、占用桥面车道、易造成交通拥堵等缺点。

为加快检测速度，提高效率，实现桥梁检测自动化，国内外学者进行了大量研究［1－4］，如南京理工大学、哈尔滨工业大学、日本大阪市立大学对爬壁机器人进行了深入研究；广东工业大学提出一种智能视频桥梁检测车，通过液压伸缩臂装置将图像采集装置安置在桥梁底面，采集桥梁病害视频；Je-Keun Oh等提出并设计了一种桥梁自动检测系统，该系统由桥梁检测车、轨道和图像采集系统三部分组成；张登峰等设计了一种桥梁检测车，通过控制器控制云台的转动，拍摄桥梁底面各个位置的图像，依靠图像处理技术进行处理识别。

在无人机桥梁检测研究方面，王小莉提出了四旋翼飞行器的几种关键技术，包括数学建模、硬件设计、PN码定位法、姿态估计法等［5］；陶晓力等采用无人机配备高倍变焦摄像头的方法采集桥梁裂缝图像，试验验证该方法具有较好的效果［6］。

综上所述，无人机可以作为先进的检测工具应用在桥梁的裂缝检测中。本文规划无人机的检测飞行路线，重点采集桥梁底面的裂缝，运用数字图像处理技术进行裂缝分类，以验证利用无人机进行桥梁检测的可行性。

1 无人机在桥梁底面检测中的应用

1.1 无人机简介

为了采集桥梁底面的正摄图像，选择大疆公司的M210RTK无人机。M210RTK无人机配备性能强劲的Flight Autonomy系统，帮助飞行器避障，机顶的红外传感器更能提供上方避障保护。配合RTK（Real-time kinematic）载波相位分差技术，无人机的悬停精度可以达到±0.1m，云台安置在无人机上部，可控制镜头与桥梁底面保持垂直。相机的镜头采用定焦镜头，焦距为50mm，可拍摄2 400万像素的图片。无人机平台顶部安装有激光测距传感器，在定点拍照时可以实时记录相机到桥梁底面的距离H。无人机进行桥梁检测对于定位精度要求较高，飞行前应实测当地风速，风速小于2m·s－1时方可飞行，天气应晴朗、少云。

1.2 相机的标定

为了提高拍摄的精度，获得较好的成像质量，无人机应尽可能地在距离桥梁底面近的位置拍摄，但同时也要保证一张照片所拍摄的实际面积足够大，故需要合理确定拍摄距离h和焦距f。

钢筋混凝土梁不同部位的允许最大裂缝宽度在0.25～0.5mm 不等，而定检中要求观测到0.02 mm以上的裂缝。桥梁结构中的真实裂缝不是规则的直线或曲线裂缝，因此宽度至少需要2个像素显示。单张图像表示面积为60mm×40mm，可以采用如下步骤粗略测定镜头的拍摄距离。

（1）在一张白纸上，画2条相互垂直且等分的线段A、B，A长度为60mm，B长度为40mm，将白纸固定在平整的墙壁上。

（2）将相机放置在三脚架上，调整三脚架的位置、高度，使相机垂直于墙壁。

（3）移动三脚架，使白纸上的2条线段在长宽2个方向正好出现在取景器。

（4）反复用钢尺测量镜头到白纸之间的距离，求得平均值为500mm［7］。

可以确定，焦距f固定时，当拍摄距离h＝500 mm时，拍摄图片的实际面积为60mm×40mm，单个像素占0.01mm2。由于无人机悬停精度误差为±0.1m，所以拍摄距离h不是定值，当拍摄距离h变化，而焦距f固定时，由凸透镜成像原理可知

式中：P1为拍摄距离为h1时像素的大小；P2为拍摄距离为h2时像素的大小。

每次定位拍摄时高度信息记录在照片中，确定了拍摄距离h后，可以求出像素的大小P，从而求得裂缝的面积。

1.3 无人机飞行航迹的规划

由于裂缝宽度较窄，为了能够识别裂缝病害，需要近距离拍摄。单张图像所覆盖的面积较小，检测一跨桥梁就需要几千张图片，难以确定裂缝在桥梁的具体位置，也就无法为养护部门提供准确的信息。为此采用有序拍摄编号法，对不同的构件进行分类编号。在进行桥梁底面检测前将桥梁底面按照单张所拍面积大小分块，确定各子块的中心坐标，将坐标转换成世界坐标系，输入到无人机地面站，使无人机按照图1顺序飞行，在子块中心悬停拍摄。如编号为511500的照片表示第5跨第1行第1列位置，距桥底距离为500mm。

图1 无人机飞行航迹

2 图像预处理

2.1 桥梁底面裂缝特征

桥梁底面裂缝的特征主要有以下2点。

（1）一幅裂缝图像包括3个部分，大部分为背景，小部分为裂缝、噪声。噪声部分的灰度值往往和裂缝部分灰度值有一部分重叠。

（2）与整个桥梁底面相比，裂缝所占的面积只是很小的一部分，即裂缝的像素数远小于背景部分的像素数。

2.2 图像灰度化及灰度校正

由于颜色对于桥梁裂缝图像的处理不产生影响，而且灰度图像在计算量和计算速度方面占有优势，故先将彩色图像统一转化为灰度图像。假设用f（i，j）表示一幅灰度图像，采用 MATLAB批量处理图片。转换函数rgb2gray实现图像灰度化的原理为：根据重要性及其他指标，将RGB图像中的R、G、B三个分量以不同的权值加权平均［8］，即

之后，用一个对数函数对图像的每一个像素灰度做对数变换，用于压缩输入图像中高灰度区的对比度，从而扩展低灰度值。为了避免对求对数，对f求对数改为对（f＋1）求对数，再以尺度比例常数C增加其动态调整范围［9］。

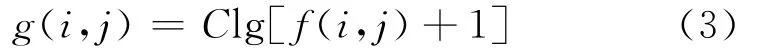
运用MATLAB对裂缝图像进行变换，结果如图2、3所示。从效果可以看出，对数变换能够扩展低值灰度，压缩高值灰度，使低值灰度的图像细节更容易看清。

图2 竖向裂缝

图3 对数变换后的图像

2.3 中值滤波去噪

根据已有研究成果，方形的滤波窗口对于有较长的轮廓线物体的图像有较好的滤波效果。研究对象是裂缝，它具有较长的轮廓线，所以采用3×3、5×5、7×7不同的滤波模板，对加了椒盐噪声的灰度图像进行滤波处理，原图和滤波后图像如图4～7所示。

图4 添加椒盐噪声

图5 3×3模板滤波

图6 5×5模板滤波

采用3种中值滤波器对图像分别进行了滤波处理，但噪声仍然存在。尝试先用3×3的滤波器对图像进行滤波，然后再利用5×5的滤波器对滤波后的图像进行二次滤波，观察滤波后图像效果，如图8所示。

2.4 基于八方向的Sobel算子的边缘检测

图7 7×7模板滤波

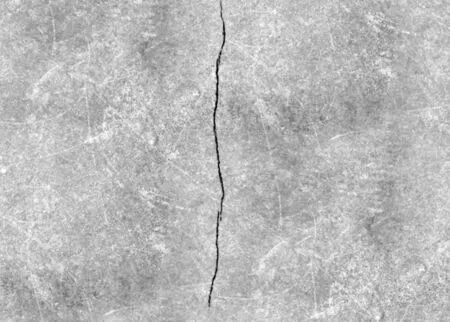
图8 3×3、5×5模板滤波

由于检测图像的裂缝特征在裂缝的各个方向都有，采用传统的Sobel算子会造成漏检，使部分边缘细节丢失。故依据裂缝图像的边缘特征，采用0°、45°、90°、135°、180°、225°、270°、315°八个方向的 Sobel算子进行检测，检测模板如图9所示。

该算法分别利用八方向模板与对应的图像数据进行卷积做近似计算。算法取8个缓存中灰度值较大的作为当前像素输出值，最大值所对应的模板方向就是该点的边缘方向。遍历图像后，所有8个方向的算子均卷积一次，取所有像素点卷积的最大值组成梯度幅值图像。任意点像素点的表达式为

利用MATLAB进行仿真后，得到传统Sobel算子和八方向改进Sobel算子的效果图，如图10、11所示。

2.5 噪声形态学去除

由于照片并非是在理想条件下获取的，桥梁底部会存在各种水渍、粉笔标记、水泥斑点等，虽然尽可能地完善了光照条件，选用了较好的飞行器材、高端的相机镜头，也采用合理的算法对图像进行增强处理、滤波去噪，但二值化后的图像仍然存在许多噪声。为了获得纯净的裂缝二值图像，选用合适大小的结构元素，以形态学闭运算的方法，对二值图像进行处理，去除细小孔洞。

图9 八方向模板

3 基于BP神经网络的桥梁裂缝分类

经过上述算法处理后，可以得到较为清晰的二值图像。虽然通过人眼观察，可以清楚无误地分别清楚图像中否含有裂缝，但是每座桥会产生大量的照片，为了节省人工劳作时间，更加准确地测量出病害的面积，对桥梁做出科学、快速、准确的评价，故对裂缝图像进行特征提取，进行特征向量的描述，并基于这些特征向量构造BP神经网络，利用该网络进行自动化的分类识别工作。

图10 Sobel算子

图11 八方向Sobel算子

3.1 裂缝特征向量的选择

假设存在一幅二值图像R（i，j），大小为M×N，其中背景部分是黑色像素，灰度值为0，目标部分是白色像素，灰度值为1。利用函数sum（R）进行计算，若sum（R）＜U，则该照片不含裂缝；若sum（R）＞U，则该照片中含有裂缝，U 为经统计得出的经验阈值。对二值图像R（i，j）分别在X轴、45°轴、Y轴、135°轴上进行投影，然后以投影轴为横轴，以与投影方向垂直的目标像素的灰度值之和为纵坐标绘图。

X轴的投影公式为

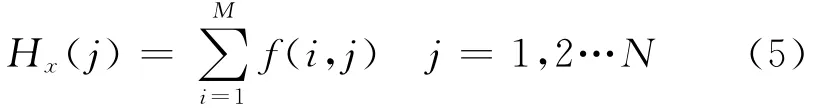
Y轴的投影公式为

45°轴的投影公式为

135°轴的投影公式为

其中的投影原理是：在X轴上的投影是在y方向上的所有像素为1的和；在Y轴上的投影是在x方向上的所有像素为1的和；在45°轴上的投影是首先将大小为M×N的二值图像R（i，j）逆时针旋转45°，变为大小为P×Q、在135°方向上的所有像素为1的和；在135°轴上的投影是首先将二值图像顺时针旋转45°，在45°方向上的所有像素为1的和。5种典型裂缝图片经过上述处理后分别向X轴、45°轴、Y 轴、135°轴投影，如图12～16所示。

图12 横向裂缝各轴投影

图13 纵向裂缝各轴投影

经分析可得出以下结论。

（1）横向裂缝向X轴的投影相对平缓，峰值较小，波动范围较分散；向Y轴的投影出现一个明显的波峰，波动范围较为集中；向45°、135°轴的投影相对平缓，峰值较小，波动范围较分散。

图14 45°裂缝各轴投影

图15 135°方向裂缝各轴投影

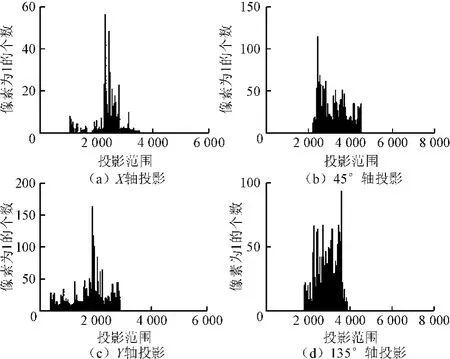
图16 网状裂缝各轴投影

（2）纵向裂缝向Y轴的投影相对平缓，峰值较小，波动范围较分散；向X轴的投影出现一个明显的波峰，波动范围较集中；向45°、135°轴的投影相对平缓，峰值较小，波动范围较分散。

（3）45°斜向裂缝向45°轴的投影相对平缓，峰值较小，波动范围较分散；向135°轴的投影出现一个明显的波峰，波动范围较为集中；向X、Y轴的投影相对平缓，峰值较小，波动范围较分散。

（4）135°斜向裂缝向135°轴的投影相对平缓，峰值较小，波动范围较分散；向45°轴的投影出现一个明显的波峰，波动范围较为集中；向X、Y轴的投影相对平缓，峰值较小，波动范围较分散。

综上可知，网状裂缝向各个轴的投影均比较平缓，峰值较小，波动范围分散。

3.2 建立BP神经网络

本文选择4层BP神经网络进行裂缝的分类，包含两个隐含层。神经网络结构见图17。

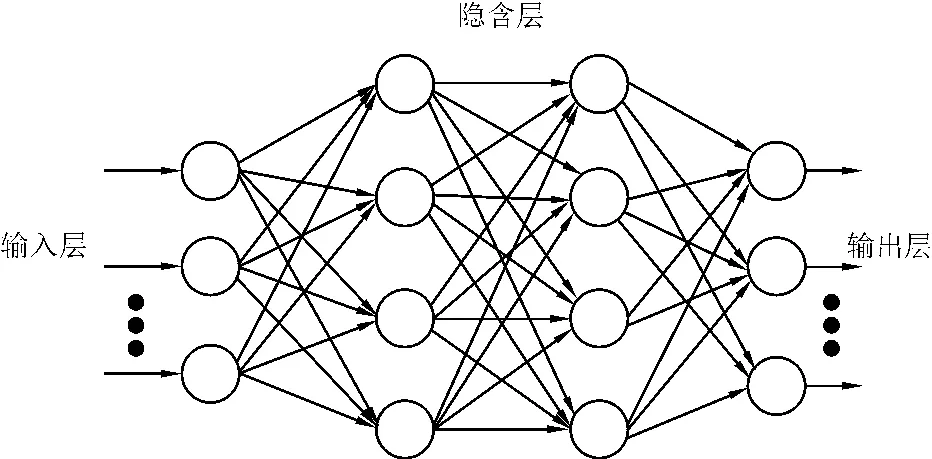
图17 神经网络结构

输入向量：P＝｛D1，D2，D3，D4，G1，G2，G3，G4，S，NUM｝。

D1、D2、D3、D4分别表示向 X 轴、45°轴、Y 轴、135°轴投影后纵坐标的差值；G1、G2、G3、G4分别表示向 X 轴、45°轴、Y 轴、135°轴投影后的投影范围；S是图片中裂缝的像素为1的点的个数，即像素的面积；NUM是连通域的个数。

经过多次试验，选择隐含层为2，隐含神经元个数为 60。输出向量 T＝ ｛00001，00010，00100，01000，10000｝代表5种情况，即横向裂缝表示为00001，45°方向裂缝表示为00010，纵向裂缝表示为00100，135°方向裂缝表示为01000，网状裂缝表示为10000。经过多次试验，神经网络的学习率设置为0.1。输入层与隐含层的连接函数为TANSIG，隐含层与输出层的连接函数为PURELIN。学习函数为TRAINLM。

使用MATLAB中的神经网络工具箱，对350幅样本图像进行训练，其中各个状态的裂缝均匀分布，打乱顺序，随机选择前300张图像进行训练，分别经过3次、4次、5次、8次迭代后停止，得到训练好的神经网络net1、net2、net3、net4，如图18～21所示。然后，将剩余的50幅图像进行仿真分类，与真实的裂缝情况进行比较，分类的正确率分别为98%、92%、96%、94%，平均正确率在90%以上。误判率为2%、8%、4%、6%，即分别有1幅、4幅、2幅、3幅被误判为其他裂缝。

图18 net1训练结果

图19 net2训练结果

图20 net3训练结果

图21 net4训练结果

4 结 语

针对不断发展的桥梁检测事业，本文提出将无人机应用于实际桥梁检测，通过规划无人机飞行路线，采集大量桥梁病害图片，结合数字图像处理技术、BP神经网络技术对裂缝图像进行分类，裂缝分类识别正确率均在90%以上。研究结果表明，基于无人机视觉的桥梁检测方案具有自动化程度高、速度快及准确率高的优点，为桥梁检测提供了新的途径。