记者图片

第一次参加MSI的喻文波（ID：Jackeylove）在iG小组赛第一场比赛开打前在座位上笑的格外阳光。

2018年，这个还未满18岁的孩子第一次来到洲际赛的舞台，这是他职业生涯里参加的首次国际性比赛。和队员同行的俱乐部工作人员在洲际赛之后说，喻文波在比赛前一天的晚上一直到凌晨五点才入睡，第一次参加大型综合赛事的兴奋和紧张，两种情绪反复交织在少年的心上。而也就是在几个月之后，少年捧杯夺冠，iG为LPL赛区带来了第一个S赛冠军。从辗转反侧心事重重到如今谈笑风生心怀大志，喻文波经历了飞跃式的成长，也成为了LPL赛区新一代年轻选手中的领军人物。

MSI半决赛首日，来自LCS赛区的Team Liquid战胜LPL的冠军代表队iG顺利闯入决赛，在接受主持人余霜的赛后采访时，Team Liquid的ADC选手彭亦亮（ID：Doublelift）难以控制心中的激动，在镜头前笑的非常开心，并表示“这一切就像做梦”。

由于LCS赛区去年综合赛事上的成绩低迷，今年MSI不得不参加入围赛。TL战队犹如黑马一般，一路过关斩将闯入决赛，成为第一大爆冷。在取得决赛名额的之后，他很快在Twitter上更新了一条状态——“对不起我的粉丝们……哦没事了。”与他去年在MSI小组赛告别赛场的落寞背影形成了鲜明的对比。从2013年就征战赛场至今的老将彭亦亮终于有幸站在决赛的舞台，十年磨一剑，对他个人而言最后的比赛无论输赢，都将是他职业生涯里最具纪念意义的一场比赛。

MSI总决赛现场一位最特别的粉丝——G2中单选手Caps的父亲正挥舞着手上的两根充气棒，为台上比赛的儿子加油打气。

2019LEC赛区转会期间，中单选手Caps从效力两年的战队Fnatic转会至G2，原G2的中单选手Perkz在得知此消息后主动要求更换至ADC位。一直以“Baby Faker”的外号被大家熟知的Caps有一张长不大的娃娃脸，与他在赛场上激进果断的风格相差甚远，也正是这样巨大的反差让他成功收获了许多粉丝，其中最为他疯狂的莫过于他的父亲。这位白发的老人一直跟随着儿子的脚步，在现场认真观看他的每一场比赛。从Fnatic到G2，Caps的父亲身上始终穿着跟儿子一样的队服，背后的ID也用心地改成了“Caps‘Dad”。舐犢情深，无论Caps最终比赛的结果如何，在台上比赛的儿子永远都是他眼中的骄傲。

LCK的冠军战队SKT再次来到了MSI，他们出场之后所有媒体的聚光灯和镜头都对准了这支战队，而他们背后则是今年MSI最后的冠军奖杯。

2017年全球总决赛结束后，未能成功卫冕的SKT在LCK也没能重振雄风，失去MSI的机会之后又接连错失了2018年的S赛。随着今年战队的重组，SKT不惜重金更换了班底，除明星选手Faker之外其余各个位置均有调整。尽管消失在公众视野多时，重新回归赛场之后这三个字母仍然是媒体最关心的队伍。随着品牌升级，SKT战队在2019年LCK夏季赛将正式更名为“T1”战队，这也是“SKT”这个队名参加的最后一届MSI。

本土作战的越南赛区冠军战队DBL在小组赛期间仅尝一胜，最终只能微笑告别赛场。

尽管实力相差悬殊，但是越南战队在赛场上展示了不同于整个亚洲的打法，以打野为核心的凶猛攻势，虽然在队员配合和选手的个人操作上有些粗糙，但仍不失为一种新的思路。近年来东南亚地区游戏产业飞速发展，电子竞技项目也应运而起，亚运会之后，越来越多的第三世界国家开始组建创办自己的职业俱乐部，东南亚市场成为未来海外赛事发展不容缺失的重要板块。

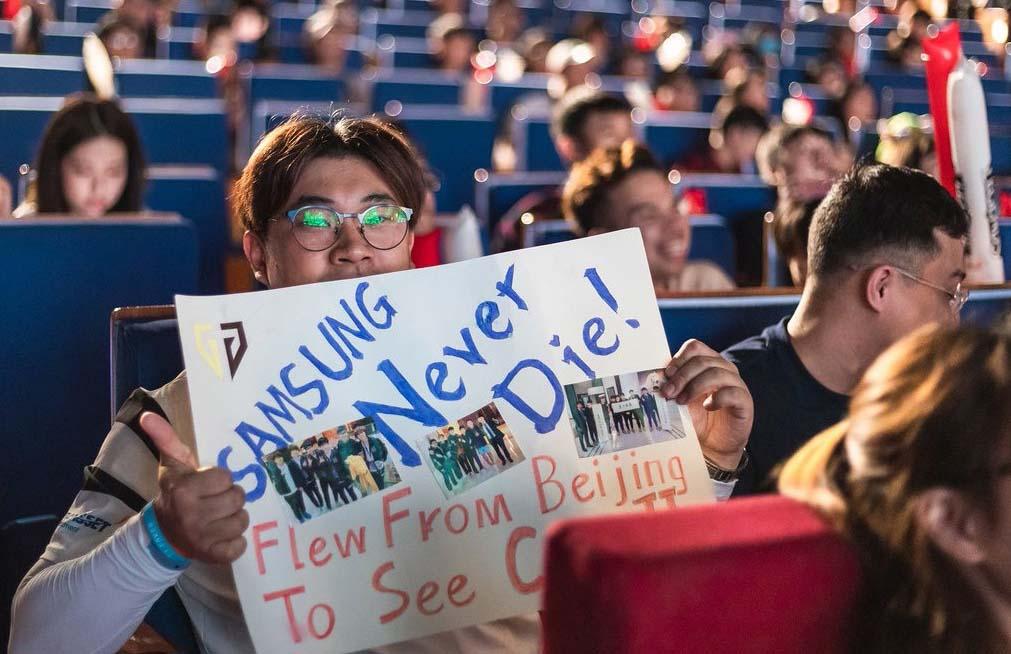
现场一位很特别的粉丝，在应援牌上手写绘制“三星永不言弃”，同时还表示自己特意从北京飞往越南，就为了见到Core JJ。

在2017年夺得S赛冠军之后，原Sumsung战队正式更名为KSV，随后又再次改名为Gen.G。或许是失去了来自队名的庇佑，夺冠一年之后Gen.G早已不复当年，止步小组赛成为了LCK赛区有史以来成绩最差的队伍。也正是在此之后，效力队伍多年的打野选手Ambition宣布退役，其余队员也纷纷远赴各个赛区。当年的冠军辅助Core.J J最终选择加入北美顶级豪门战队TL，成功帮TL补足了下路对线的疲软，提升了队伍对全局的把控，让TL在北美赛区屹立不倒的同时也能与其他赛区的顶尖战队一较高下。