斜拉桥钻石型主塔承台受力分析研究
宋炜
(上海市政工程设计研究总院(集团)有限公司,上海市 200092)
0 引言
典型的斜拉桥主要由主梁、拉索、主塔及基础四部分组成。主塔作为斜拉桥的主要承重构件,承担着将作用于主梁及其自身的各类荷载作用传至基础的功能;同时主塔也是最能表达斜拉桥个性和视觉效果的结构物,因此,城市中的斜拉桥需要更多地从造型、景观及环境协调等建筑艺术方面的要求来确定主塔的结构型式。
斜拉桥主塔常见的结构型式有独柱型、A型、倒Y型、门型、H型、钻石或花瓶型等各种型式[1],如图1所示。其中钻石型主塔造型优美,稳定感强,该塔型主要特点是横向刚度大,在横向荷载作用下索塔受力性能良好,同时下塔柱倾斜向内靠拢,大大减小承台及基础尺寸,因此在桥面宽度有一定要求的大跨径斜拉桥中应用较为广泛。但由于两侧下塔柱内倾固结于整体式承台上,承台横向受力较大,且与传统承台有所不同。本文针对钻石型主塔承台构造特点,分别采用杆系模型及三维实体有限元分析方法对其受力情况进行分析研究。

图1 斜拉桥主塔的各种结构型式
1 工程概况
新井冈山大桥位于江西省吉安市主城区,是吉安市二环线的重要越江通道。跨赣江主桥采用(150+150)m独塔双索面结合梁斜拉桥,桥宽38.0m,主塔采用弧形钻石型桥塔,总高约125.0m,其中下塔柱高度为19.9m,塔柱中心线内倾斜度为2.8∶1,采用变截面单箱单室箱形截面,如图2所示,为保证塔底反力均匀传递到主塔承台上,塔底设置2m厚塔座。

图2 新井冈山大桥斜拉桥主桥
主塔基础位于赣江河道深水区,承台顺桥向为17.0 m,横桥向约为52.5 m,厚为5.0 m,两端设圆端尖角,以减少对水流的影响,如图3所示。基础采用22根直径2.5m钻孔灌注桩,梅花形布置,桩基持力层为中风化含砾泥质砂岩,按嵌岩桩设计。
根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[2](以下简称桥涵规范)及参考文献[3],目前承台设计主要可概括为两类:一类是将承台作为受弯构件,按“梁式体系”进行抗弯、抗剪承载力计算;另一类是按“撑杆-系杆体系”的拉压杆模型进行分析。桥涵规范中对这两类设计方法的适用条件进行了规定,显然,主塔承台顺桥向受力符合“撑杆-系杆体系”计算模式,而横桥向受力较为复杂,上述计算模式是否适用有待进一步研究。本文仅对承台横桥向受力展开分析。
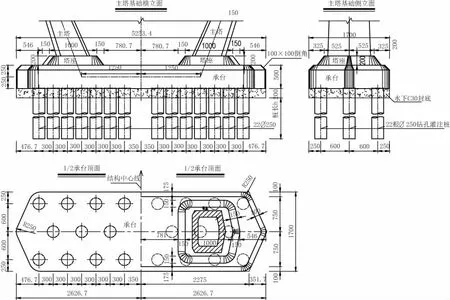
图3 主塔承台基础结构布置图(单位:cm)
2 分析模型及荷载
2.1 分析模型
采用三维结构分析软件M ID A S C i v i l进行分析,首先将主塔承台按“梁式体系”简化为杆系模型,承台采用等效至截面中心处的梁单元模拟,主塔下塔柱保留一定长度并延伸至承台与其刚接,承台底桩基础取10m处固结,并根据桩基实际长度对其轴向刚度进行修正[4],承台简化的杆系模型如图4所示。
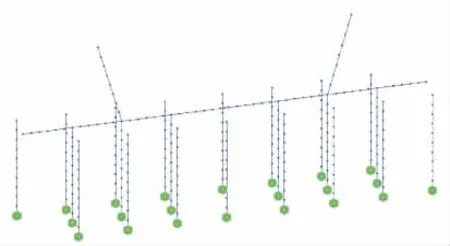
图4 主塔承台简化杆系模型
同时,为了对承台进行更为精细化地分析,并与杆系模型相比较,建立承台实体有限元模型,如图5所示。

图5 主塔承台实体有限元模型
根据圣维南原理,实体模型中承台顶保留一定长度的下塔柱,荷载通过刚臂等效分摊施加于顶端全断面。桩基础同样采用梁单元,并取桩长10m位置嵌固,桩顶节点与承台底接触区域内节点通过刚臂约束,以保证不同单元变形耦合。
2.2 输入荷载
将主桥总体计算得到的主塔下塔柱相应位置处单元内力作为输入荷载,反向作用于上述承台模型的塔柱顶端,这里仅取成桥阶段作用标准组合下的塔柱内力进行分析,其中标准组合包括恒载、活载、温度效应、风荷载及基础不均匀沉降等作用。
此外,塔柱单元内力需由其单元局部坐标系转换至整体坐标系,模型输入荷载值见表1。

表1 主塔承台模型输入荷载
3 结果分析及研究
3.1 承台杆系模型与实体模型计算对比
根据桥涵规范,该工程钻石型主塔承台部分桩基离塔柱边缘距离大于承台厚度,可作为受弯构件按“梁式体系”进行受力分析。对此,首先通过两种模型对承台内力分布进行对比。
显然,承台简化杆系模型很容易得到承台内力图,而对于实体模型,需将不同位置截面所切的所有实体单元应力进行积分,方可得到相应截面的等效内力。这里主要关心承台顺桥向弯矩My,如图6和图7所示,分别对承台跨中位置及与塔柱轴线相交处截面所有单元应力进行积分,得到相应等效截面弯矩My(这里X轴、Y轴分别为水平横桥向及顺桥向,Z轴为竖向)。

图6 承台塔柱轴线相交处截面实体模型切面应力积分(单位:kN·m)

图7 承台塔中位置实体模型切面应力积分(单位:kN·m)
以此进一步计算,承台对应两种分析模型不同位置处顺桥向弯矩分布如图8所示。
可以看到,两种模型计算结果差异较大,其中承台中部及与塔柱固结区段,杆系模型所得弯矩普遍比实体模型计算值大(绝对数值),而在承台塔柱固结点附近,杆系模型由于无法考虑固结区域内力扩散等影响,其值远远高于实体计算结果。

图8 主塔承台两种模型顺桥向弯矩分布对比(单位:kN·m)
选择承台部分关键断面,如图9所示,分别对其杆系模型及实体模型的顺桥向弯矩计算结果进行比较,见表2,由于杆系模型难以考虑塔柱截面范围内弯矩折减,其结果不具有可比性,故这里仅取塔柱底外边缘所对应的承台截面。

图9 承台对比分析部分截面位置

表2 主塔承台两种模型顺桥向弯矩计算对比
由以上对比可以看出,相较于实体有限元分析,采用杆系模型梁单元方法进行的承台受力计算虽然趋势大致相同,但结果偏于保守,特别是塔柱与承台固结区域,所得结果与实际受力相差很大。对于此类承台,杆系模型分析方法具有一定局限性,为了更准确地反映其空间力学效应往往需要建立更精细化的三维实体有限元模型。
3.2 承台塔座影响分析
为保证主塔塔柱内力均匀传递至承台,往往在塔底承台顶设置一定厚度的塔座,该工程塔底亦设有2m厚塔座。
为了对承台受力计算时塔座的影响进行研究,在上述承台实体模型基础上,建立一不含塔座的承台实体有限元模型,如图10所示,其余包括边界及荷载模拟等则完全相同。

图10 主塔承台实体有限元模型(无塔座)
对此,标准组合作用下,有无塔座的两种承台实体模型,其等效顺桥向弯矩分布对比如图11所示。
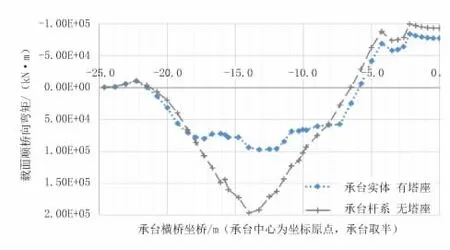
图11 承台实体模型有无塔座顺桥向弯矩对比(单位:kN·m)
很明显,除塔座局部范围外,两模型计算结果较为接近;而塔座区段内,不考虑塔座影响时,承台弯矩出现峰值,有塔座模型此区段弯矩分布则较为均匀。这说明经过塔座的过渡及扩散,承台与塔柱固结区域的弯矩出现明显削减。
同样,对于前面定义的4个关键截面,不含塔座的承台实体模型顺桥向弯矩值与前述杆系模型及(含塔座)实体模型计算结果对比见表3。
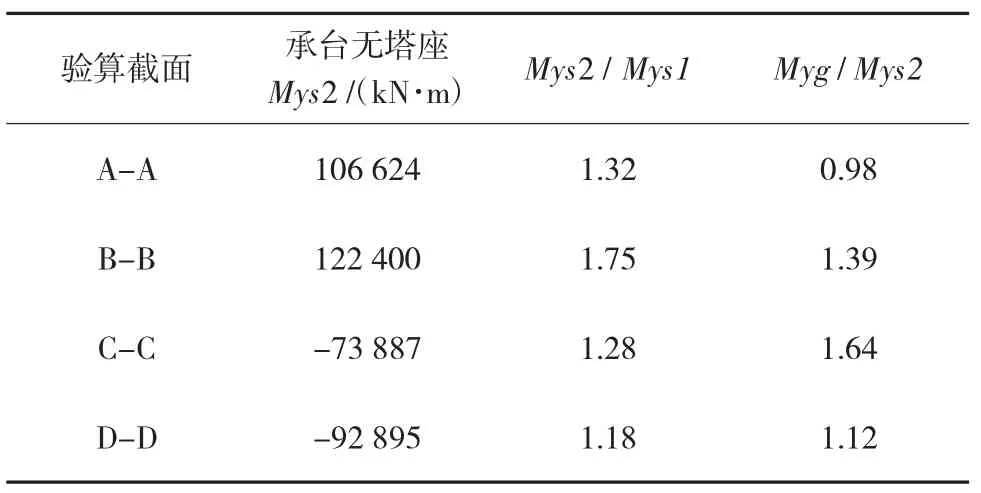
表3 主塔承台实体模型塔座影响对比
可以看到,若不考虑塔座影响,标准组合作用下承台跨中截面顺桥向弯矩增大约18%,塔座范围更是相差超过30%,承台部分区段受力有与杆系模型类似的趋势,这表明塔座对于传递扩散塔底内力、改善承台受力的作用较为明显。
3.3 承台应力结果
进一步,对有无塔座两种承台实体模型的顺桥向正应力及主拉应力进行对比如图12~图15所示。

图12 主塔承台横桥向正应力对比(承台实体有塔座)(单位:MPa)
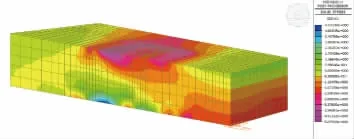
图13 主塔承台横桥向正应力对比(承台实体无塔座)(单位:MPa)

图14 主塔承台横桥向主拉应力对比(承台实体有塔座)(单位:MPa)

图15 主塔承台横桥向主拉应力对比(承台实体无塔座)(单位:MPa)
由于钻石型主塔下塔柱内倾,下塔柱轴力传递至承台使其中间区段受压,同时下塔柱内力使承台产生顺桥向弯矩My(前面已对此进行分析),两者相叠加后,承台中间区段表现为上缘受拉,下缘受压,但最大应力均在2MPa以内。
塔柱作用范围内的承台顶部均受压,所不同的是,考虑塔座影响时,顶部最大压应力为4.1MPa,主要分布于塔座内侧边缘,而不考虑塔座时最大压应力约为5.1 MPa,分布在塔臂与承台接触区域;与塔柱固结段承台底部局部受拉,对应有无塔座的最大拉应力分别为3.1MPa、4.6 MPa,主拉应力最大值亦集中在此范围内。
3.4 不同模型的桩基反力对比
标准组合作用下,分别对承台杆系模型及有无塔座的实体模型的桩基反力分布情况进行分析,如图16所示。
由于承台受力对称,仅选取不同模型下相同四分之一承台对应的7根桩基反力进行对比,其桩基编号布置及反力值见表4。

图16 不同模型桩基反力分布情况(单位:kN)

表4 不同模型桩基反力计算值对比
可以看到,不同模型的最大竖向反力桩基位置相同,均位于中间排第2列,即均为⑥号桩,所不同的是其反力数值,其中杆系模型最大,而考虑塔座影响的承台实体模型最小。此外,有塔座的承台实体模型其桩基反力分布最均匀,而杆系模型变化最大。
这表明杆系模型难以考虑承台空间受力分布效应,同时在一定程度上,塔座的设置使承台荷载传递及桩基反力分配更为均匀。
4 结语
以吉安市新井冈山大桥工程为背景,对其主桥主塔承台分别建立梁单元杆系模型及三维实体有限元模型,对钻石型主塔倾斜式塔柱传力下的承台受力情况及桩基反力分配等问题进行了分析探讨,研究表明此类内倾塔柱下的整体式承台受力按杆系模型进行计算偏于保守,且有一定局限性,往往需要借助于更精细化的实体有限元分析;同时,承台顶所设塔座对扩散塔柱内力、改善承台受力效果较为明显,也一定程度上使桩基反力分配更为均匀。研究结果可对此类承台的分析计算及配筋设计提供一定参考。

