土石混填路基振动压实值与动态变形模量相关性研究

张海欧， 孙 韬， 余 旭

(西南交通大学土木工程学院， 四川成都 610031)

为克服传统路基压实程度检验指标评价不全面，且费时费力的缺点，近年来，以振动压实值(VCV)作为路基质量控制指标为代表的连续压实控制技术因其具有全面、快速、省时、省力及针对性强的优点，在我国的路基工程中得到了越来越多的应用,为此，一些学者进行了相关的研究工作。黄志福[1]等人发现振动轮加速度与路面压实度之间具有明显的正线性相关性；张家玲[2]将经过一定信号处理的振动轮加速度定义为振动压实值(VCV)，并发现VCV与路基结构抗力或反作用力之间呈线性关系；徐光辉[3]等发现级配碎石压实过程中结构抗力与压实程度之间存在较好的线性相关性，说明了路基的结构抗力是可以用来评价路基结构的压实状态的；张家玲[4]等通过对两个填石路堤试验段的振动压实值与常规荷载板类指标之间关系的分析，发现振动压实值与常规载荷板类指标具有线性相关关系；常丹[5]等指出一些常规指标之间具有很高的线性相关程度。

相关学者的研究工作主要集中在反映压实质量的各种指标之间是否具有相关性以及相关性大小等方面，而对土石混填路基连续压实控制指标与传统指标线性相关性及其影响因素的研究尚不多见。本文通过对某高速公路土石混填路基不同压实工艺下所测得的振动压实值VCV与动态变形模量(Evd)的线性相关性进行分析，对VCV值与Evd值线性相关性的影响因素做出探讨。

1 连续压实控制技术与Evd测试原理

1.1 连续压实控制技术原理

连续压实控制技术基本原理是连续测量振动压路机振动轮的动态响应信号，经过一定的后续信号处理，以形成对路基压实质量的评价指标。目前国外进行连续压实控制技术的研究的主体以企业单位为主[7-8]，这些企业单位分别形成了各自的评价指标，如谐波比、动态模量、刚度系数等[9]。国内的西南交通大学等单位，开发了以振动压实值为路基质量控制指标的连续压实控制技术，在国内也有较为广泛的应用。但所有的连续压实控制指标都需先与常规指标建立联系之后才可在实际工程中应用。

1.2 Evd测试原理[10]

动态变形模量Evd值是指经过一定质量(通常为10 kg)的落锤冲击，对半径为15 cm的载荷板(视为刚性)施加一定大小(7.07 kN)和作用时间(18 ms)的冲击荷载，从而测定土体在该冲击荷载作用下抵抗变形能力的参数，标定的载荷板下最大动应力为0.1 MPa，动态变形模量计算如式(1)所示。

Evd=1.5rσ/S=22.5/S

(1)

式中：r为载荷板半径(150 mm)，σ为最大动应力(0.1 MPa)，S为载荷板沉降量，单位为mm。

2 现场试验

2.1 试验工点概况

该高速公路路基填筑试验工点里程为K8+105～K8+341，此工点中心最大填高19.2 m，边坡最大高度19.8 m，地基采用冲击碾压处理。该处工点所用原始填料为强风化-全风化花岗片麻岩与砂砾的土石混合体(本文称为A类填料，如图1所示)、中风化-强风化花岗片麻岩与砂砾的土石混合体(本文称为B类填料，如图2所示)。填料过60 mm与200 mm方孔筛，筛得数据如表1所示，现场所用填料中A类填料位于表层20 cm范围内，在碾压完成后基本成为填筑层表层砂砾，而B类填料相较于上层A类填料具有较高的强度，且位于填筑层的下部，在压实完成后，破碎程度较低。

图2 B类填料

表1 填料粒径范围质量比

2.2 现场试验方案

在填筑过程中使用的压路机为26 t，22 t自重的振动压路机，两种压路机主要参数如表2所示。

表2 振动压器机主要参数

现场试验段选取轮迹长度为20 m，每种工况的测点数如表3所示；填筑层厚度分别为70 cm、60 cm、50 cm，其中70 cm厚的填筑层下部50 cm为B类填料(图1)，上部20 cm为A类填料(图2)；依据现场施工情况，具体的现场试验工况如表3所示，

工况5至工况9所用填料全部为A类填料，工况1至工况4所用填料上部20 cm为A类填料，下部为B类填料，试验时具体过程如下：在进行连续压实检测之前对填料进行预压与整平，在预压1～2遍之后，使用整平机进行表面整平；布置连续压实检测轮迹与Evd检测点位；在压路机测试轮迹与Evd测点布置完成之后，将连续压实测试装置的传感器置于压路机振动轮处，进行连续压实检测试验(图3)；每一遍检测完成之后，在测点上进行Evd的检测(图4)，依次循环，直至填筑层碾压完成。

3 数据处理

3.1 VCV与Evd线性相关性分析方法

振动压实值VCV与Evd之间的相关关系一般情况下被

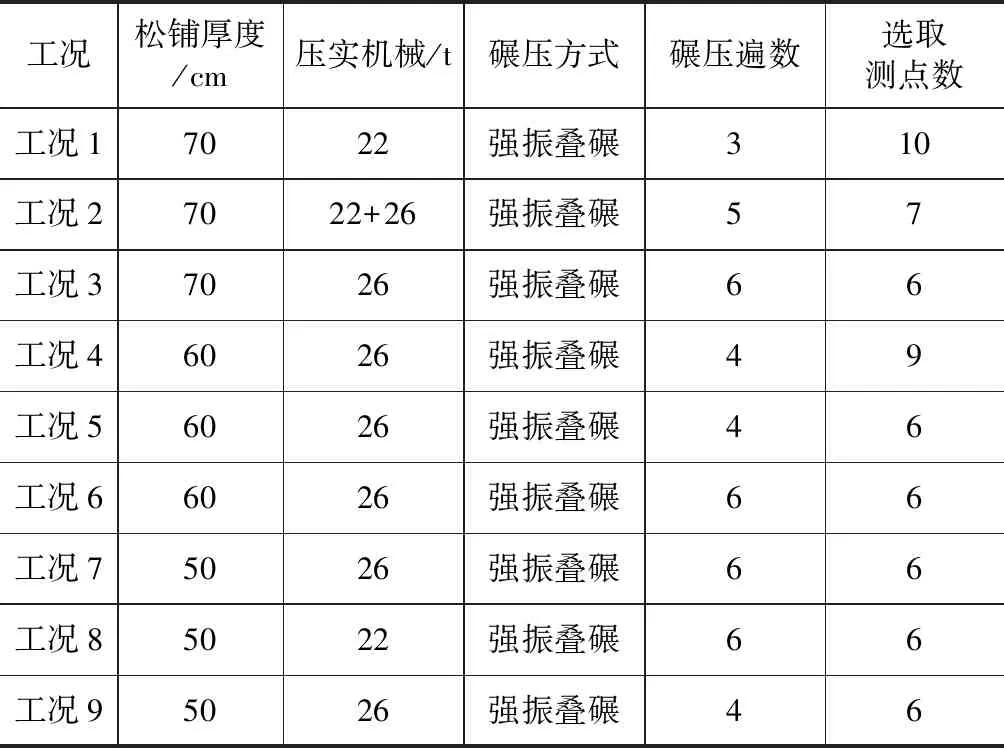
表3 试验工况表

图3 连续压实检测

图4 Evd值检测

认为是直线关系[4]：

y=a+bx

(2)；

式中y在此处表示Evd值，x表示振动压实值VCV值；a、b为回归系数，可按式(3)、式(4)确定。

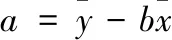
(3)；

(4)；

依据相关性校验试验的要求[11]，取测点所测Evd值与对应VCV曲线上的VCV值计算相关系数。其中连续压实指标与常规指标之间线性相关性系数按(5)式计算。当R>0.7时，即可认为VCV与Evd之间存在的线性相关性强。

(5)；

由试验情况对各工况采集到的数据进行线性相关性分析，每种工况中VCV值与Evd值之间的线性相关性系数与回归方程如表4所示，在本文中，当线性相关性系数R>0.7时，认为两指标之间具有强线性相关性，给出线性回归方程并作出回归图线，否则认为两指标间的线性相关性弱，不给出线性回归方程，但仍对数据进行分析讨论。

表4 各工况线性相关系数与回归方程

3.2 线性相关性及其影响因素分析

结合表3与表4，即可对碾压遍数、压实机械、松铺厚度三种因素对两种指标之间线性相关性之间的影响进行具体分析。考察全部9种工况，只有3种(松铺厚度为50 cm时)具有强线性相关性，在这三种工况中可以建立振动压实值与动态变形模量之间的回归方程，为该三种工况下的路基连续压实检测提供参考。

3.2.1 碾压遍数的影响

对比工况5与工况6以及工况9(回归曲线如图5所示)与工况7(回归曲线如图6所示)，两种指标的线性相关性系数分别从0.677减至0.663和从0.851减至0.772，亦即在60 cm与50 cm的松铺厚度与26 t振动压路机的碾压下，当碾压遍数由4增至6时，两指标之间的线性相关系数有所下降，原因是表层填料在振动压路机的碾压下，表层的填料在被破碎、挤压、填充后形成较为坚实的表层砂砾，在此过程中，VCV值随着填筑层抗力的增大而增大，填筑层的变形能力不断地减小。当碾压遍数达到一定数值的时候，压路机继续施加的振动能可以对填筑层更深处施加影响，并将深部的大粒径块砾石破碎填充至骨架空隙之中使之密实，因此地基结构的抗力与持续增加，但Evd值由于仪器的影响深度限制，只能测得填筑层较浅处的动态变形模量，导致其数值不再继续增加。因此数据的离散性增大，其线性相关性系数减小。

图5 工况9 Evd与VCV关系

图6 工况7 Evd与VCV关系

3.2.2 压实机械的影响

工况7与工况8(回归曲线如图7所示)两种指标的线性相关性系数从0.772减小至0.728，即在50 cm的松铺厚度与碾压遍数同时为6遍的情况下，将压实机械从26 t振动压路机换成22 t振动压路机后，两指标之间的线性相关性系数减小，可能的原因是VCV值是一个压路机轮宽范围内的平均值，而Evd值仅为半径为150 mm圆范围的检测值，可以视为一个点的测值，其数据的离散性受填筑层的均匀程度以及测试仪器的影响范围的影响较大，由于填筑层松铺厚度较薄，两种压路机都可以影响到填筑层的较深处甚至底部，其中26 t的振动压路机相较于22 t振动压路机对填筑层施加的能量更大，其内部的大粒径砾石破碎率较高，因而数据的离散性更小，线性相关性更高。

图7 工况8 Evd与VCV关系

3.2.3 松铺厚度的影响

工况3、工况6与工况7中，随着填筑层松铺厚度的减小，两指标之间的线性相关性有较为明显的增强，其中的原因是，越薄的松铺厚度，从表层到深部的大粒径块砾石越容易为压路机的振动能所破碎，在碾压完成后填筑层中所遗留的大粒径块砾石越少，填筑层越均匀，因而测得的数据的离散性越小，两指标之间的线性相关性越大。

3.2.4 填料类型的影响

需要特别指出的是，工况4与工况5，这两种工况摊铺的填料种类并不完全相同，工况4中，填筑层表层20 cm内铺设的为A类填料，底部40 cm为B类填料，而在工况5中，整个填筑层的填料全部为A类填料。在这两种工况中，工况4的线性相关系数为0.504，工况5的线性相关系数为0.677，可见，当填料的整体强度较小时，大粒径的块砾石更容易被破碎为细小的颗粒，填筑层的均匀性更好，两指标之间的线性相关系更强。

4 结论

本文通过分析现场试验数据，研究了无黏性土石混合填料路基连续压实检测指标振动压实值VCV值与动态变形模量Evd之间在各种工况下的线性相关性，分析了碾压遍数、压实机械、松铺厚度对二者之间线性相关性的影响，主要得出如下结论：

(1)由于Evd测试仪器相较于振动压路机的影响深度要浅，导致较为浅层部位测得的Evd值不能很好地随反应填筑层更深部情况的VCV值的增大(减小)而增大(减小)，当碾压遍数由4遍增至6遍时，压路机可以影响填筑层的更深处，而Evd值无法反映这种影响，导致两指标之间的线性相关系数有所下降。亦即，过多的碾压遍数并不能提高两指标之间的线性相关性。

(2)对于较薄的填筑层，更重的压实机械对填筑层施加的能量更大，其内部的大粒径砾石破碎率较高，填筑层均匀性较好，可以提高两种指标之间的线性相关性。

(3)较薄的松铺厚度，从表层到深部的大粒径块砾石越容易为压路机的振动能所破碎，在碾压完成后填筑层填筑层越均匀，测得的数据的离散性越小，两指标之间的线性相关性越大。

(4)对于土石混合填料而言，填筑层所用填料的类型对两指标之间的线性相关性也有较大的影响，母岩风化程度高的填料相较于风化程度较低的填料更易于破碎与压实，压实后的均匀性也较好，测得的两种指标之间的线性相关性较强。

(5)可能影响两种指标间的因素还有许多，例如操作误差、测试的影响范围以及数据的处理方式等，本文的研究并不全面，须待后期作进一步的研究。