衰减系数对移动列车脉动风速谱的影响
邹淇炀, 张泽田, 高 慰
(西南交通大学桥梁工程系,四川成都 610031)
为探究车辆以及桥梁在侧风作用下的动力响应,首先需要模拟作用于桥上以及列车车辆上的脉动风速时程。Shinozuka[1]等首先将谱解法应用于风场模拟。Cooper[2]指出,基于泰勒湍流冻结假定与各向同性湍流假定,可以由固定点的脉动风速谱推导得到移动列车的脉动风速谱。吴梦雪[3]、李小珍、肖军等人[4]对该方法进行了改进,通过维纳辛钦定理,分别得到了半解析与全解析的移动列车脉动风速谱模型。该脉动风速谱模型可以考虑列车速度与风速比以及来流风向角对于移动列车脉动风速谱的影响。通过单变量随机过程模拟,可以快速得到移动列车的脉动风速时程。
在模拟桥上固定点以及移动列车的脉动风速场时,需要考虑模拟点之间在空间以及频率上的相关性。该相关性可以由相干函数进行刻画。目前,工程上常用的相干函数模型为Davenport提出的指数形势下的模型。
事实上,由于该模型中的衰减系数为经验系数,其取值并不固定。本文主要探讨采用不同的衰减系数取值,对于移动列车的脉动风速谱的而影响。
1 谐波合成法
1.1 谱解法
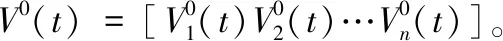
(1)
互谱函数与自谱函数有如下关系:
(2)
式中:Coh(Δij;ω)为i和j点相干函数。
可以证明,相干函数矩阵可以通过Cholesky分解得到如下所示的下三角矩阵与上三角矩阵的乘积:
Coh(ω)=D(ω)DT(ω)
(3)
因此,根据Deodatis[5]的理论,随机过程Vj(t)可以由式(4)模拟。
cos(ωmlt-θjm(ωml)+φml)},(j=1,2,…,n)
(4)
式中:N为一充分大的正整数,Δω为频率增量,Δω=ω/N,ωup为上限截止频率;φml为均匀分布于[0,2π]的随机相位角;θ为矩阵D(ω)的复角,在风场模拟过程中,该复角的取值为0。ωml为双索引频率下的频率增量,并表示为:
(5)
为保证模拟结果不失真,根据采样理论,其时间增量需满足:Δt≤2π/2ωup。
另外,该模拟过程可以通过FFT算法进行加速。
1.2 移动列车脉动风速时程模拟
为了获得移动列车的脉动风速时程,传统的做法基于静止模拟点的脉动风速时程样本,利用离散点提取与插值算法相结合得到。在随机模拟中,静止模拟点的间距设置为Δy=V·Δt,其中V为移动列车的运行速度。则对于移动列车,其在p时刻的瞬时脉动风速值即为j点在p时刻的风速。
1.3 相干函数
空间上两个模拟点之间的相干性可以用相干函数刻画。常用的模型有为Davenport相干函数模型,对于脉动风的纵向成分,可以用式6来表达:
(6)
其中k为衰减系数,Uz为高度z处的平均风速。衰减系数k为经验系数。
曹映泓等人[6]指出,对于等间距分布的静止模拟点,其指数形式下的相干函数,在进行Cholesky分解时,可以通过显示分解直接得到:
Dij(ωml)=αm·cos(α)j-m
(7)
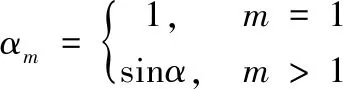
cosα=γ21(ω)/γ11(ω)
2 静止模拟点校验
为检验上述方法在移动列车脉动风场模拟中的可靠性,在高度z=40m上,以间距为10 m平均布置了100个静止模拟点。在该高度处,平均风速Uz取为30 m/s;上限截止频率ωup=8π,共划分为1 024个频段,M=2N;模拟时间增量Δt=0.125s。目标谱采用式(8)所示的Kaimal谱:
(8)
其中:f=nz/Uz为无量纲化频率,u*为摩擦速度,z0为地表粗糙高度。
Davenport相干函数模型中的衰减系数取为16。如图1所示可以看出模拟得到的固定点脉动风场的自谱与目标谱均拟合较好。
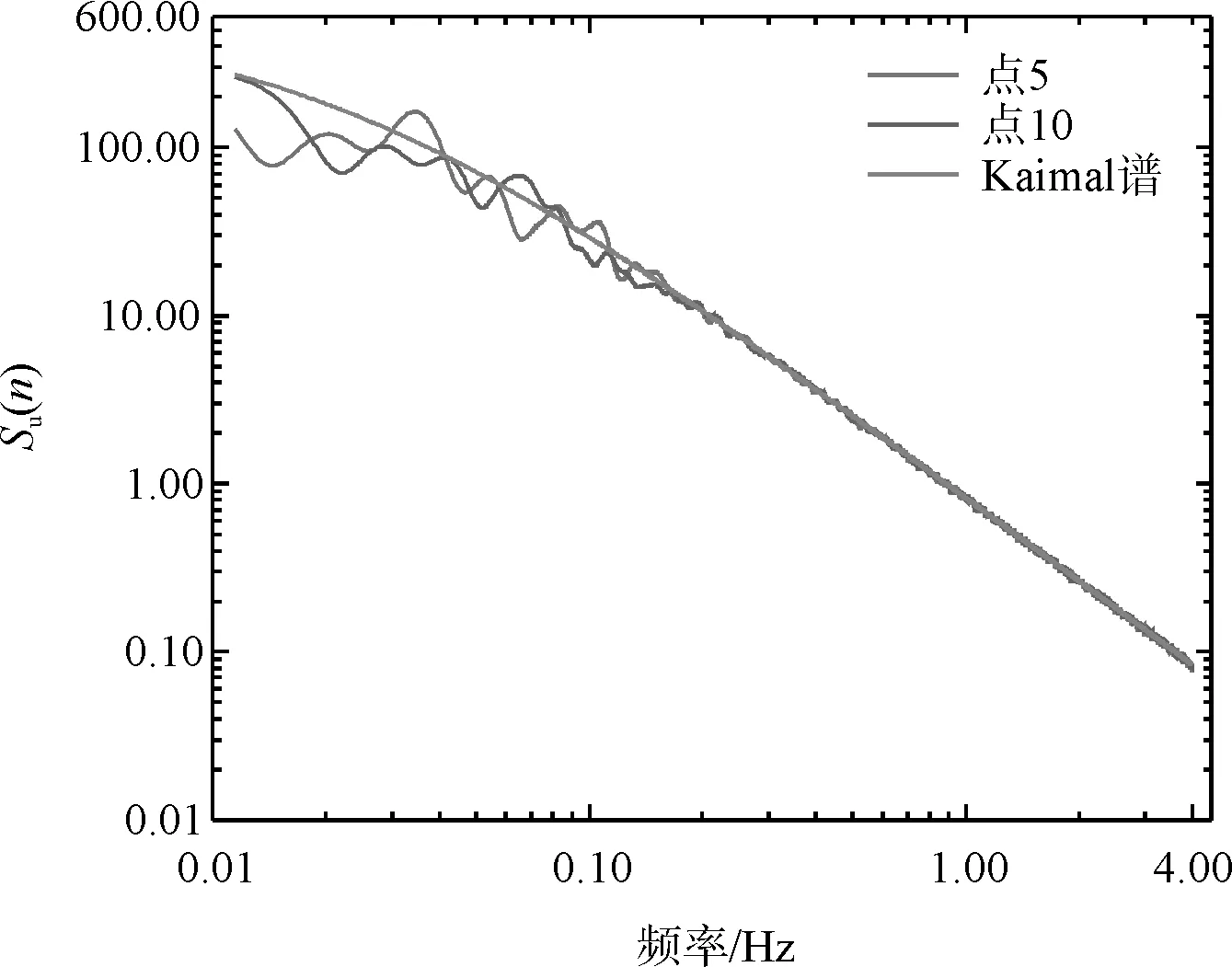
图1 静止模拟点脉动风速谱模拟
3 衰减系数的影响
对于Davenport相干函数模型,当衰减系数不同时,相干函数的值在低频段有较大的差异。由图1可知移动列车的脉动风速谱能量主要集中于低频段,该低频段的能量增大现象可能会对移动列车的脉动风速谱造成较大的影响。
采用Davenport提出的相干函数模型,通过取不同的衰减系数值,考虑衰减系数对于移动列车脉动风速场的影响。在工程应用中,衰减系数k的取值通常为7~17。因此在本文中,分别模拟k=7、k=10、k=17情况下移动列车的脉动风速谱。如图2所示为移动列车运行速度为V=30m/s与V=60m/s情况下,取不同衰减系数时,移动列车脉动风速谱的比较。
可以看出,对于Davenport相干函数,随着衰减系数的增大,移动列车的脉动风速谱有着明显的向高频移动的趋势。该现象与随着速度的增大,移动列车的脉动风速谱所展现的多普勒效应相吻合。事实上,由相干函数的模型可以看出,衰减系数的增大,导致相邻两点之间的相关度减小,这一效应与移动列车运行速度增大的效应是相同的。因此,在工程计算中,通常可以较为保守地取经验值中较大的值,以保证工程的安全性。

(a) V=30m/s
4 结论
基于Davenport相干函数模型,采用多变量随机过程模拟方法,对移动列车脉动风速时程继续你行模拟,通过频谱分析得到了移动列车的脉动风速谱。分析不同衰减系数下的移动列车脉动风速谱,可以看出不同的衰减系数会对移动点脉动风速谱产生较大的影响。

