空调用摆动转子压缩机摩擦损失分析
李 伟 潘 曦 饶金强 潘树林
空调用摆动转子压缩机摩擦损失分析
李 伟1潘 曦2饶金强1潘树林1
(1.广西大学机械工程学院 南宁 530004;2.西安交通大学能源与动力工程学院 西安 710049)
对摆动转子压缩机各运动件进行运动分析和受力分析,建立了空调用摆动转子压缩机摩擦损失数学模型,并运用MATLAB编程求解,结果表明摆动转子与偏心轮之间的摩擦损失最大,其次是主副轴承的摩擦损失,再次是摆杆与导轨间的摩擦损失。通过与滚动转子压缩机摩擦损失情况对比,摆动转子压缩机虽然有效消除了滑板顶端与转子间的摩擦,但转子与偏心轮之间的摩擦损失大幅高于滚动转子压缩机。研究结果为摆动转子压缩机设计提供参考。
摆动转子压缩机;运动分析;受力分析;摩擦损失;数学模型
0 引言
自上世纪70年代摆动转子机构提出以来,一直普遍应用于空气压缩机和真空泵中,但由于当时加工技术的限制,很少应用于空调压缩机中[1]。直到90年代,随着人们环保意识的增强和对制冷剂的深入研究,更加环保的替代制冷剂HFC提出并应用[2,3],由此对压缩机的性能有了更高的要求。摆动转子压缩机是滚动转子压缩机的孪生结构,在具有其优点的同时,较之有更好的承压能力,更高的容积效率等优势,因此又被重新关注与研究,甚至被个别企业大量制造生产[4-6]。
能源与环境问题已经成为人类所共同关心的重要话题,因此机器的效率成为衡量压缩机优劣的重要指标。摆动转子压缩机的机械效率直接影响压缩机的性能并影响整个空调系统。目前,已有许多学者研究滚动转子压缩机的摩擦损失[7,8],而对摆动转子压缩机的摩擦损失研究较少。本文参照滚动转子压缩机的相关计算与分析方法,建立摆动转子压缩机摩擦损失数学模型,并对摩擦损失进行分析计算,所做工作为摆动转子压缩机设计提供依据。
1 结构与工作原理
摆动转子压缩机结构如图1所示,主要零部件包括:气缸、摆动转子、偏心轮轴、导轨、两端盖以及端盖上所装设的排气阀等。摆动转子压缩机将滚环和滑板做成一体,形成独立零件——摆动转子,其滚环部分套在偏心轮上,摆杆部分可在导轨中上下滑动并随导轨左右摆动。摆动转子将气缸分为两个工作腔,随着偏心轮轴的转动,两工作腔容积周期性地扩大与缩小,从而实现工质的吸入、压缩及排出。摆动转子压缩机两工作腔同时工作,偏心轮轴每旋转一圈,压缩机便完成一次工作循环。
1—气缸;2—排气口;3—导轨;4—吸气口;5—摆动转子;6—偏心轮轴
2 摩擦损失数学模型的建立
2.1 运动分析及其模型
摆动转子压缩机中的主要运动件有偏心轮轴、摆动转子以及导轨。其中,偏心轮轴近似为匀速旋转,导轨作定心摆动,摆动转子则作复杂的平面运动。
摆动转子压缩机的运动机构为曲柄摇块机构,运动简图如图2所示,以偏心轮轴中心O为原点建立坐标系,A为摆动转子中心,B为导轨中心,曲柄OA长为偏心距,OB长为气缸与导轨中心距,摆动转子中心A距离导轨中心B为。OA绕原点以角速度匀速旋转,转角为,AC与y轴夹角为。

图2 摆动转子的运动分析
A点的速度方向垂直于OA,其大小为:
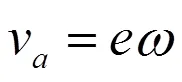
A、B两点共同在摆动转子上,B点的速度沿摆杆方向,可按照图2分解为v和v:
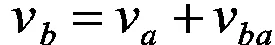

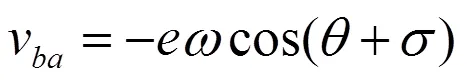
根据几何关系,摆动转子的摆动角速度与导轨摆动角速度相同:

偏心轮与滚环内壁之间相对滑动的角速度为:

摆动转子滚环外表面切点处的粘性摩擦力只在切向做功,而切向速度可以分解成两个部分:一部分是由偏心轮带动,滚环外表面在气缸壁面上形成的滑动;另一部分是因摆杆及导轨的牵制作用,由转子与偏心轮间角速度差所引起的与气缸内壁的相对滑动。因此,摆动转子与气缸切点的相对速度为两速度之和:
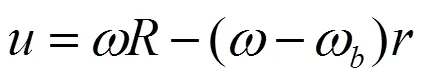
式中:为气缸半径,m;为滚环外半径,m。
摆动转子滚环外表面与气缸切点处相对速度、导轨线速度和摆杆滑动速度如图3所示;偏心轮与摆动转子之间的相对角速度和线速度如图4所示。

图3 各速度与转角关系

图4 偏心轮与摆动转子之间的相对速度
2.2 受力分析及其模型
如图5(a),摆动转子的受力较为复杂,包括:滚环所受气体作用的合力F1;摆杆上所受气体作用的合力F2;压缩机壳体内气体作用在摆杆背部的气体力F3;导轨对摆杆两侧的支持力分别为N1、N2及运动中的摩擦力F1、F2;压缩机内部各零件表面都有润滑油膜,因此压缩机工作过程中,油膜会对运动件产生粘性摩擦力;各零件运动所产生的惯性力等。
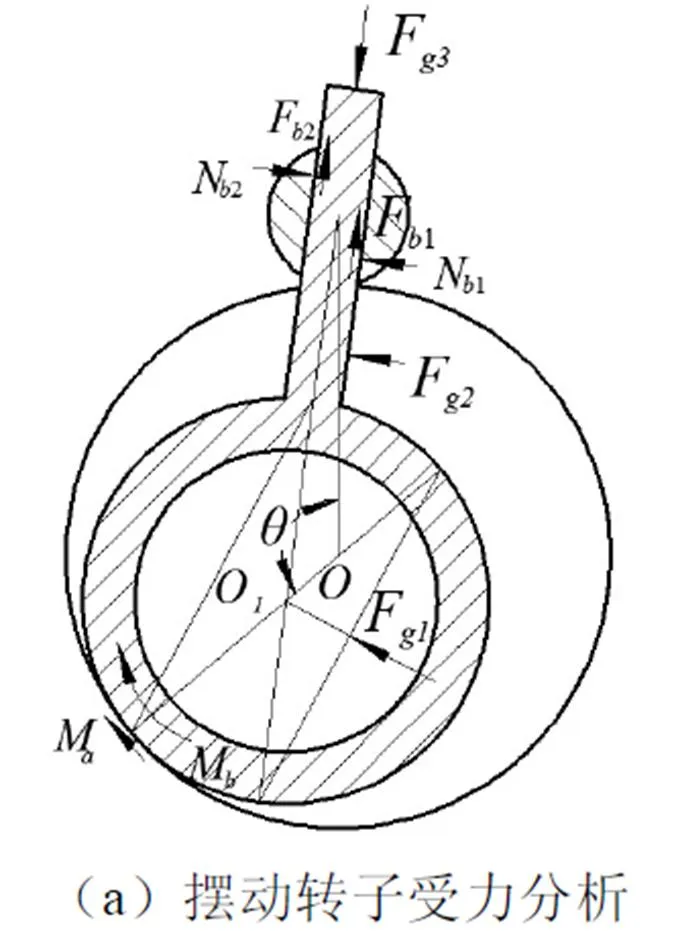
压缩机在工作过程中,摆杆背部的气体力F3在0~π内为动力矩,在π~2π内为阻力矩,整个过程合力矩为零,计算时忽略不计。
气体力F1所形成阻力矩为:

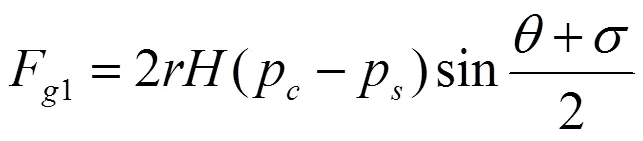
式中:p为压缩腔压力,Pa;p为吸气腔压力,Pa;为气缸高度,m。
气体力F2所形成的阻力矩为:

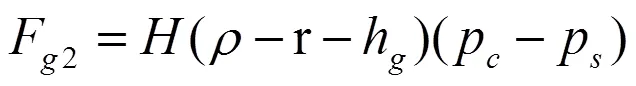
气体力形成的总阻力矩为两气体力矩之和:
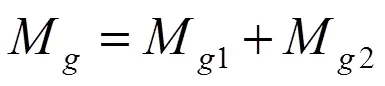
图6为气体力Fg1、Fg2随转角变化的关系曲线。
由于润滑油的存在,摆动转子与气缸内壁之间由其粘性剪切力所引起的摩擦力F及粘性摩擦力矩M为:
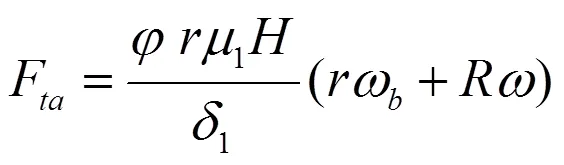
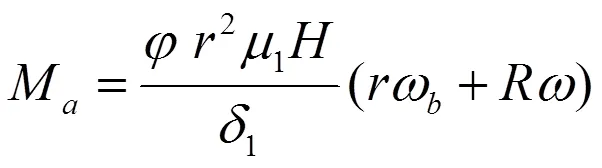
式中:1为润滑油粘度,Pa·s;1为间隙宽度,m;为径向间隙油膜弧度,rad。
摆动转子与偏心轮之间的粘性摩擦力矩为:

式中:l为偏心轮长度,m;2为间隙宽度,m;0为滚环内半径,m。
摆动转子与气缸上端盖之间的润滑状态为流体动力润滑。而摆动转子的运动可视为由绕主轴中心的旋转运动和绕偏心轮中心的摆动叠加而成[6]。利用大平板间流体润滑模型分析[7],两种运动所产生的摩擦力矩为M1和M2为:


式中:3为间隙宽度,m。
摆动转子与下端盖之间的润滑状态为边界润滑,同理,绕主轴中心旋转的摩擦力以及绕偏心轮中心摆动的摩擦力矩表示为[6]:


式中:2为边界摩擦系数;W为摆动转子重量,N。
摆动转子压缩机偏心轮轴的主副轴轴径、轴承长度均不同。取两轴与轴承径向间隙相等,则两轴承部位的摩擦力矩为[6]:
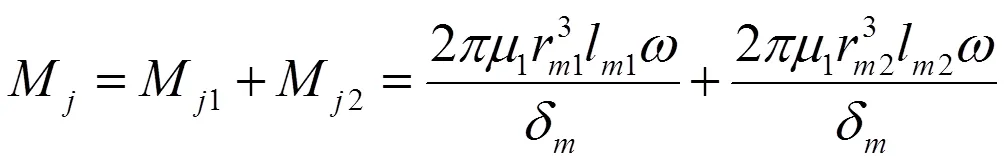
式中:r1为主轴半径,m;l1为主轴承的长度,m;δ为轴与轴承的径向间隙,m;r2为副轴半径,m;l2为副轴承的长度,m。
偏心轮轴、电机及平衡重构成压缩机的转子系统,其与气缸下端盖形成止推轴承,此处为边界润滑,产生的摩擦力矩为[6]:
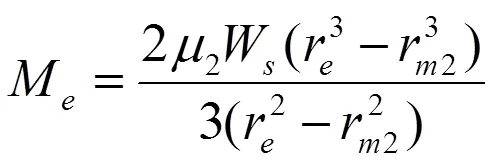
式中:r为止推面的外半径,m;W为转子系统的重量,N。
如图5(b)所示,导轨受力复杂,单独分析过于繁琐[9],故将导轨与摆动转子作为整体分析。导轨惯性力很小忽略不计;将摆杆的惯性力分解成两部分:一部分F作用在滚环中心,与滚环旋转惯性力F一起被平衡块平衡;另一部分F作用在摆杆顶端C点[6]。作力学平衡方程组:

式中:F1θ为O1点在垂直于摆杆方向分力,N;θ为惯性力F与水平正向夹角,rad;为摆杆顶端C点到O1点距离,m。
则导轨与摆杆间的摩擦力为:
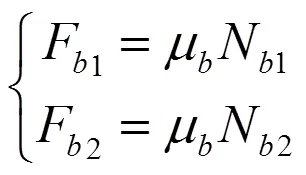
式中:b为摆杆与导轨间的摩擦系数。
取导轨与气缸间的压力和导轨与摆杆间的压力相等N=N,则气缸与导轨之间的摩擦力为:
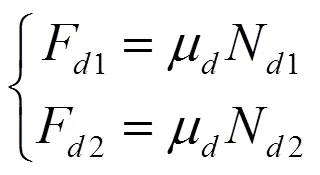
式中:d为导轨与气缸间的摩擦系数。
根据润滑理论[10],导轨和气缸之间的粘性摩擦力矩为:
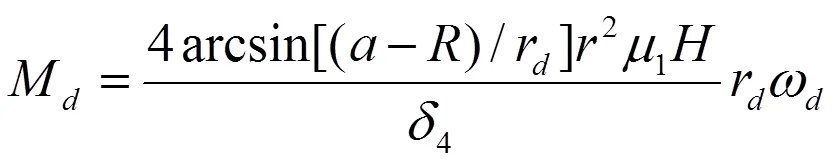
式中:4为间隙宽度,m。
3 摩擦损失计算及分析
3.1 模拟计算主要结构参数
本文运用以上数学模型,对一台采用R410A为制冷剂的空调用摆动转子压缩机进行数值模拟。样机主要参数如下:气缸直径=22mm;气缸高度=26mm;摆动转子滚环外径=17mm;摆杆及滚环厚度=4mm;气缸与导轨中心距=27mm;导轨半径r=4.5mm;电机转速=3000rpm;除滚环与气缸间隙1=20μm外,其余间隙2=3=4=δ=15μm[6];润滑油采用PVE-68,物性参数由文献[11]计算得到。
3.2 计算结果及分析
通过上述建立的摩擦损失数学模型并运用MATLAB编程求解,得到压缩机各部位的摩擦损失情况如表1所示,主要摩擦损失及总摩擦损失随转角变化曲线如图7所示。表1及图7表明,总摩擦损失随着压缩机偏心轮轴转角不断变化,其中摆动转子与偏心轮之间的摩擦损失占比最大,接近总摩擦损失的50%;其次是主副轴承的摩擦损失,约占总摩擦损失的30%;再次是摆杆与导轨间的摩擦损失,约占总摩擦损失的20%。摆动转子压缩机设计时,应注重前面三处的润滑,以提升压缩机的机械效率。

表1 摆动转子压缩机摩擦状态及损失计算
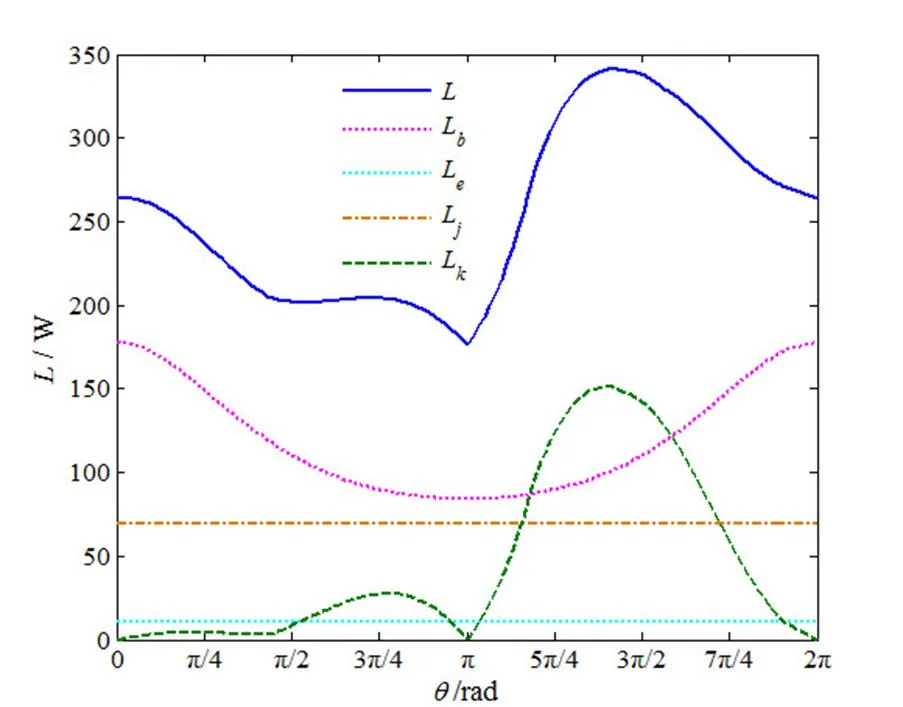
图7 主要损失及总摩擦损失随转角变化曲线
空调用滚动转子压缩机总摩擦损失中,主要摩擦损失如下:滑板与滑板槽之间摩擦损失约占28.1%;主副轴承摩擦损失约占25.2%;滑板顶端与转子之间摩擦损失约占24.3%;转子与偏心轮之间摩擦损失约占18.7%[12]。滚动转子压缩机转子与偏心轮之间摩擦损失较小,其原因是:转子与偏心轮之间相对速度较小[6]。摆动转子压缩机将摆杆与滚环做成一体,消除了滚动转子压缩机中滑板顶端与转子之间的较大摩擦损失,但由于摆动转子压缩机中转子受到摆杆与导轨的牵制,由图4可知,转子与偏心轮之间存在较大相对速度,摆动转子压缩机中转子与偏心轮之间的摩擦损失大幅高于滚动转子压缩机。
4 结论
(1)摆动转子压缩机中摆动转子与偏心轮之间的摩擦损失最大,其次是主副轴承的摩擦损失,再次是摆杆与导轨间的摩擦损失,其他各处的摩擦损失可忽略。摆动转子压缩机设计时,应重视上述三处摩擦损失较大部位的润滑。
(2)相比滚动转子压缩机而言,摆动转子压缩机消除了滚动转子压缩机中滑板顶端与转子之间的较大摩擦损失,但由于转子与偏心轮之间存在较大相对速度,摆动转子压缩机中转子与偏心轮之间的摩擦损失大幅高于滚动转子压缩机。
[1] Masuda M, Sakitani K, Yamamoto Y, et al. Development of swing compressor for alternative refrigerants[C]. In:Proceedings of the International Compressor Engineering Conference, West Lafayette: Purdue University press, 1996:499-504.
[2] 王冰霜,张云娟,宋俊峰,等.R410A直流变频列间空调系统变流量调节性能分析及试验研究[J].制冷与空调,2017,31(2):194-198.
[3] 柴玉鹏,马国远,许树学,等.R1234yf和R134a制冷及制热性能实验研究[J].制冷与空调,2017,31(4):435-440.
[4] 王满,潘树林,周盛杰.摆动转子压缩机导轨处优化设计与泄漏分析[J].制冷与空调,2017,31(3):230-234.
[5] Yamamoto Y, Kanayama T, Yuasa K, et al. Development of high efficiency swing compressor for R32 refrigerant[J]. Journal of energy and power engineering, 2015,9:161-165.
[6] 马国远,李红旗.旋转压缩机[M].北京:机械工业出版社,2001.
[7] Ito Y, Hattori H, Miura K. Numerical analysis for rotating motion of a rolling piston in rotary compressors-effective factors for characteristics of rotating motion of a rolling piston[C]. In:Proceedings of the 2010 International Compressor Engineering Conference at Purdue, Purdue University, West Lafayette, Indiana, USA, 2010:1217.
[8] 马一太,天华,李敏霞.CO2双级滚动转子压缩机不可逆损失分析[J].工程热物理学报,2012,33(2):181-185.
[9] Tanaka S, Nakahara T, Kyogoku K, et al. Lubrication characteristics between bush and blade of swing compressor[C]. In:Proceedings of the 2002 International Compressor Engineering Conference at Purdue, Purdue University, West Lafayette, Indiana, USA, 2002:1534.
[10] Cameron A. 润滑理论基础[M].北京:机械工业出版社,1980.
[11] Cai DH, He GG, Yokoyama T, el al. Simulation and comparison of leakage characteristics of R290 in rolling piston type rotary compressor[J]. International Journal Refrigeration, 2015,53:42-54.
[12] Yang J. Mechanical loss analysis of inverter controlled two cylinders type rotary compressor[C]. In:Proceedings of the 2002 International Compressor Engineering Conference at Purdue, Purdue University, West Lafayette, Indiana, USA, 2002:1516.
Analysis of Friction Losses of Swing Compressors for Air Conditioning
Li Wei1Pan Xi2Rao Jinqiang1Pan Shulin1
( 1.School of Mechanical Engineering, Guangxi University, Nanning, 530004;2.School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an, 710049 )
In this paper, the motion analysis and force analysis of the moving parts in the swing compressor are carried out. The mathematical model of friction losses in a swing compressor for air conditioning is established and solved by MATLAB programming. The results show that the friction loss between the rotor and the eccentric is the largest, followed by the friction losses of the main and secondary bearings, and the friction losses between the blade and the bushes. Compared with the friction losses in the rolling piston compressor, the friction between the vane tip and the rotor is effectively eliminated in the swing compressor, but the friction loss between the rotor and the eccentric is substantially higher than that in the rolling piston compressor. The results provide references for the design of swing compressors.
swing compressor; motion analysis; force analysis; friction loss; mathematical model
TB652
A
1671-6612(2019)03-287-06
李 伟(1991-),男,硕士研究生,研究方向为压缩机工作过程,E-mail:liweichnmail@163.com
潘树林(1970-),男,教授,博士,博士,研究方向为压缩机工作过程,E-mail:panshulin@163.com
2018-06-25

